概要
pythonでセル・オートマトンを手抜きして書きます。
arch linux, python3.5で作成しました。
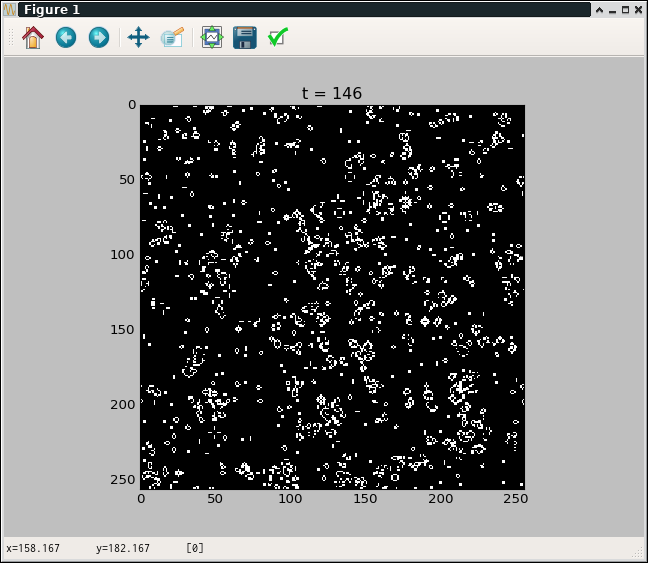
ライフゲーム
セルオートマトンをグレー画像のように処理しますと、scipyの畳み込み計算、matplitlibの画像表示機能で楽ができます。
画像として表示しているので小さくするとセルが潰れたりします。
import numpy as np
import scipy.signal
import matplotlib.pyplot as plt
h = np.array([[1, 1, 1],
[1, 0, 1],
[1, 1, 1]])
def update(U):
'''
Update rule:
current_state\N_neighbors | 0 1 2 3 4 5 6 7 8
---------------------------+----------------------------------
0 | 0 0 0 1 0 0 0 0 0
1 | 0 0 1 1 0 0 0 0 0
'''
N_neighbors = scipy.signal.convolve2d(U, h, boundary='wrap', mode='same')
U_next = np.zeros_like(U)
U_next[N_neighbors == 3] = 1
U_next[np.logical_and(N_neighbors == 2, U == 1)] = 1
return U_next
size = (256, 256)
U = np.random.randint(2,size=size)
fig = plt.figure()
ax = fig.add_subplot(111)
img = ax.imshow(U, interpolation="nearest", cmap=plt.cm.gray)
i = 0
while True:
U = update(U)
img.set_data(U)
i += 1
ax.set_title("t = {}".format(i))
plt.pause(0.01)
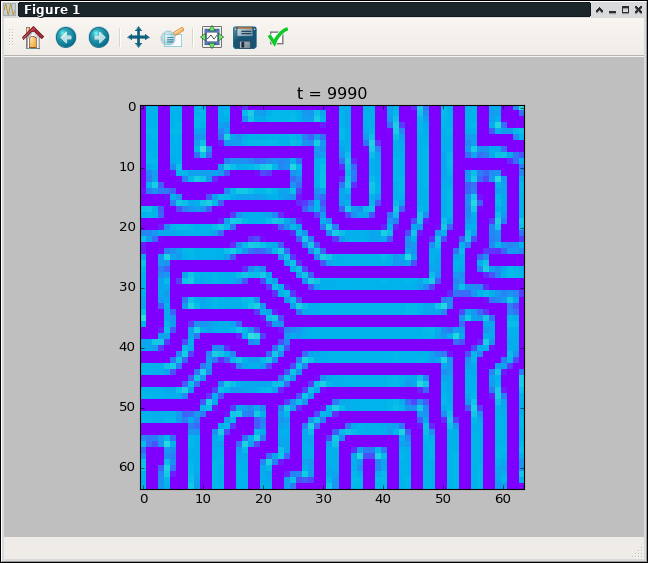
チューリング・パターン
セル・オートマトンの定義からは外れるかもしれませんが、拡散反応系も同じようにできます。
更新式は下記チューリング・パターンを使用。
\begin{align}
\frac{\partial u}{\partial t} &= D_u \nabla u + u ( 1 - u^2) - v \\
\frac{\partial v}{\partial t} &= D_v \nabla v + 3 u - 2 v
\end{align}
$u(x,y)$を画素値として表示します。$v(x,y)$は計算に使うだけ。
$D_u$, $D_v$は拡散係数になります。
この係数によって、パターンが形成されるか、されないか、発散するかが決まります。
今回は$D_u=0.2, D_v=1.8$でパターンを形成させました。(トライ&エラーで決めた)
今回は$\nabla$をscipyのラプラシアンフィルタで計算します。
import numpy as np
import scipy.ndimage.filters
import matplotlib.pyplot as plt
lap = lambda X: scipy.ndimage.filters.laplace(X)
def update(U, V, Du=0.2, Dv=1.8):
return (Du*lap(U) + U*(1.-U*U) - V,
Dv*lap(V) + 3.*U - 2.*V)
size = (64, 64)
U = np.random.random(size)
V = np.random.random(size)
dt = 0.1
fig = plt.figure()
ax = fig.add_subplot(111)
img = ax.imshow(U, interpolation="nearest", cmap=plt.cm.gray)
view_interval = 10
for i in range(10000):
dU, dV = update(U, V)
U += dt*dU
V += dt*dV
if i % view_interval == 0:
img.set_data(U)
ax.set_title("t = {}".format(i))
plt.pause(0.01)
plt.show()
更新式として代わりにフィッツフュー-南雲方程式を使うと、画像が安定化せずに振動し、生き物のように蠢きます。面白いです。