はじめに
どうもどうもこんにちは。
thunderです。
月日は早いもので、ゲームで学ぶ探索アルゴリズム実践入門を出版してから5カ月の月日が経ちました。お買い上げいただいた方には感謝の気持ちが尽きないです。
さて、ゲームで学ぶ探索アルゴリズム実践入門では、貪欲法のために設計した評価関数を、そのままビームサーチに適用して結果を改善していました。
ビームサーチに慣れている人であれば、これは自然な流れですし、困ることはないでしょう。
しかし、貪欲法だけを念頭において評価関数を設計している場合、後からビームサーチを適用すると思わぬ罠にはまる可能性があります。
本記事では、「貪欲法だとうまくいくが、ビームサーチへの適用は望ましくない評価関数」について紹介していきます。
わかる人にとっては当たり前に思えることしか書かないと思いますが、わかる人にとっての当たり前が必ずしも初学者にとって当たり前ではないかもしれません。
わかる人は温かい目で見守っていただければと思います。
対象読者
- 貪欲法(greedy)とビームサーチの概要をある程度把握している方
- ビームサーチにあまり慣れていない方
ビームサーチがわからない場合は、ゲームで学ぶ探索アルゴリズム実践入門か世界四連覇AIエンジニアがゼロから教えるゲーム木探索入門のいずれかを読むことを推奨します。逆に、ビームサーチの概要を知っている人はそれらの書籍、記事を読んでいる必要はありません。
問題設定
壁有り数字集め迷路
本記事はオリジナルゲームの壁有り数字集め迷路を用いて説明していきます。
table:壁有り数字集め迷路のルール
| 見出し | 説明 |
|---|---|
| プレイヤーの目的 | ゲーム終了時点のスコアを高くする。 |
| プレイヤーの人数 | 1人 |
| プレイヤーの着手タイミング | 1ターンに1回 |
| プレイヤーができること | 各ターン、キャラクター(@)を上下左右の四方向いずれかの場所に1マス移動させる。立ち止まること、壁のあるマスや盤面の外に移動させることはできない。 |
| ゲームの終了条件 | 4ターン経過する。 |
| その他 | キャラクターはランダムに初期配置される。 壁は全ての床がつながるようにランダムに配置される。 キャラクターが移動した先にポイントがある場合、そのポイントの値をゲームスコアに加算し、床のポイントは消失する。 |
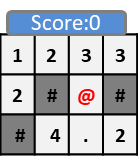
たとえば、以下のような初期状態を考えます。
キャラクター(@)は壁(#)には侵入できません。
キャラクターは1ターンに右左下上の4方向のいずれかに移動し、床に存在するポイントを取得して自身のスコアにします。
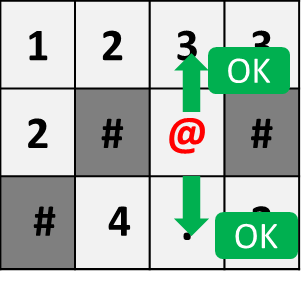
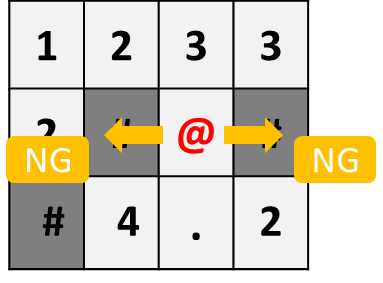
以下の場合、
下に移動して何もない床を踏んでスコア0のまま、
右に移動して床のポイント2を取得してスコア2、床のポイントは消滅、
左に移動して何もない床を踏んでスコア2のまま、
左に移動して床のポイント4を取得して最終スコア6
です。
貪欲法の評価関数設計を変えることによる結果の比較
それでは本題に入ります。
まずは貪欲法について、2種類の評価関数設計による結果の比較を見ていきましょう。
ノード(盤面)を評価する方針
これはゲームで学ぶ探索アルゴリズム実践入門か世界四連覇AIエンジニアがゼロから教えるゲーム木探索入門で紹介した方針です。
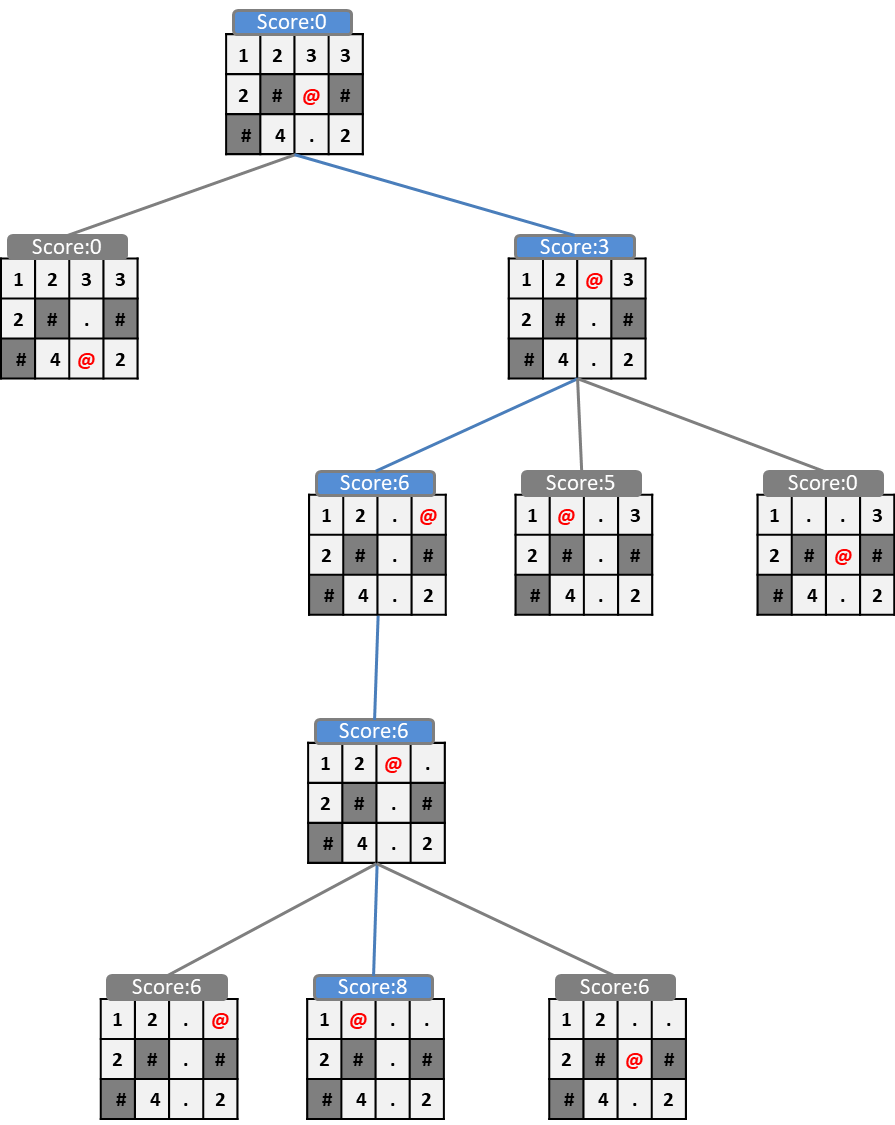
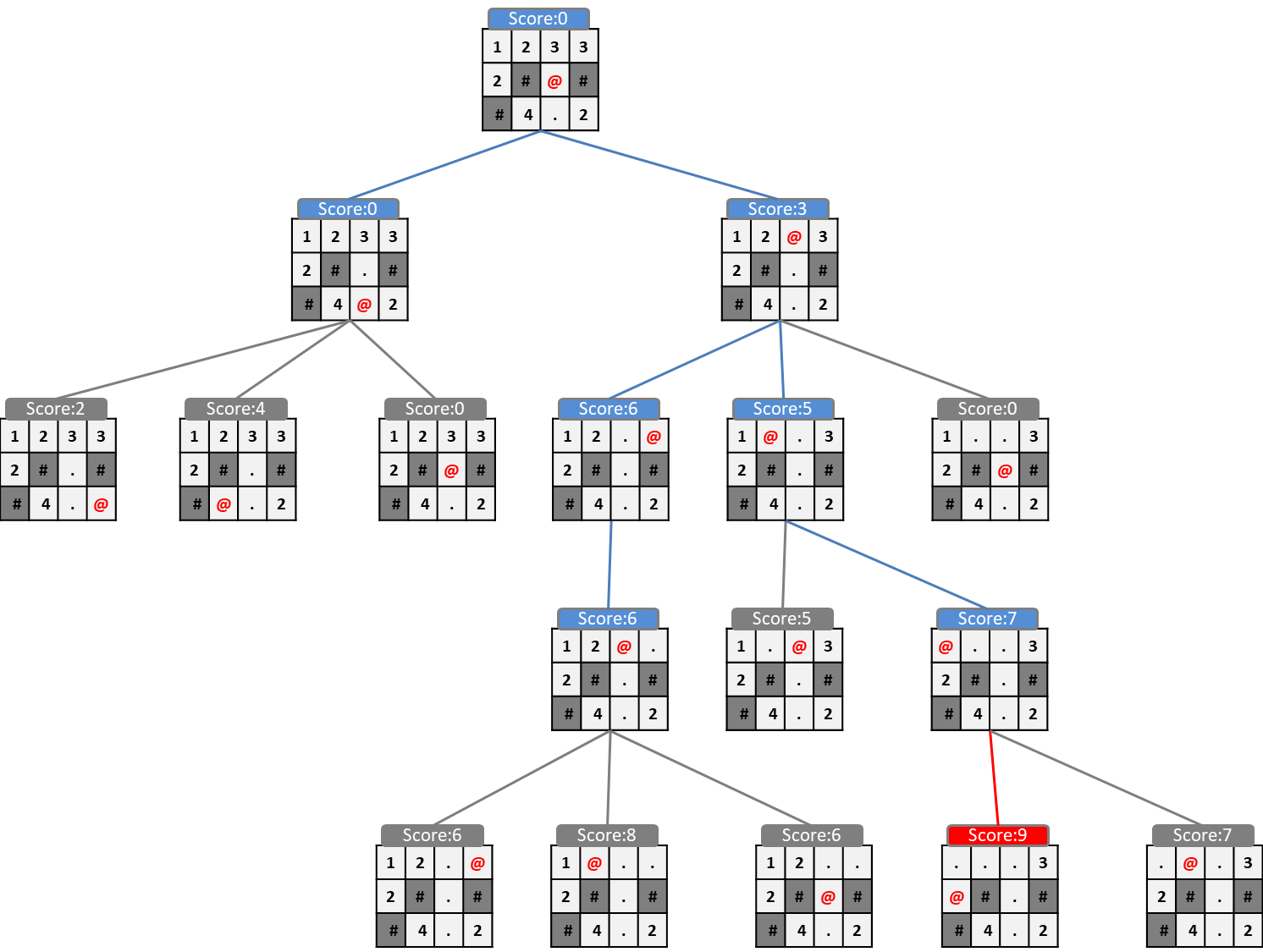
たとえば、ノードのゲームスコアをそのまま評価関数として貪欲法を適用した場合、以下のように
上移動後の盤面(スコア3)→右移動後の盤面(スコア6)→左移動後の盤面(スコア6)→左移動後の盤面(スコア8)
と遷移して最終スコアは8となります。
エッジ(遷移)を評価する方針
さて、貪欲法の場合、親ノードから子ノードに遷移することで得られるスコアを評価しても充分な結果が得られます。
壁有り数字集め迷路の場合、各ターンで取得した床のポイントをそのノードの評価としてもいいです。
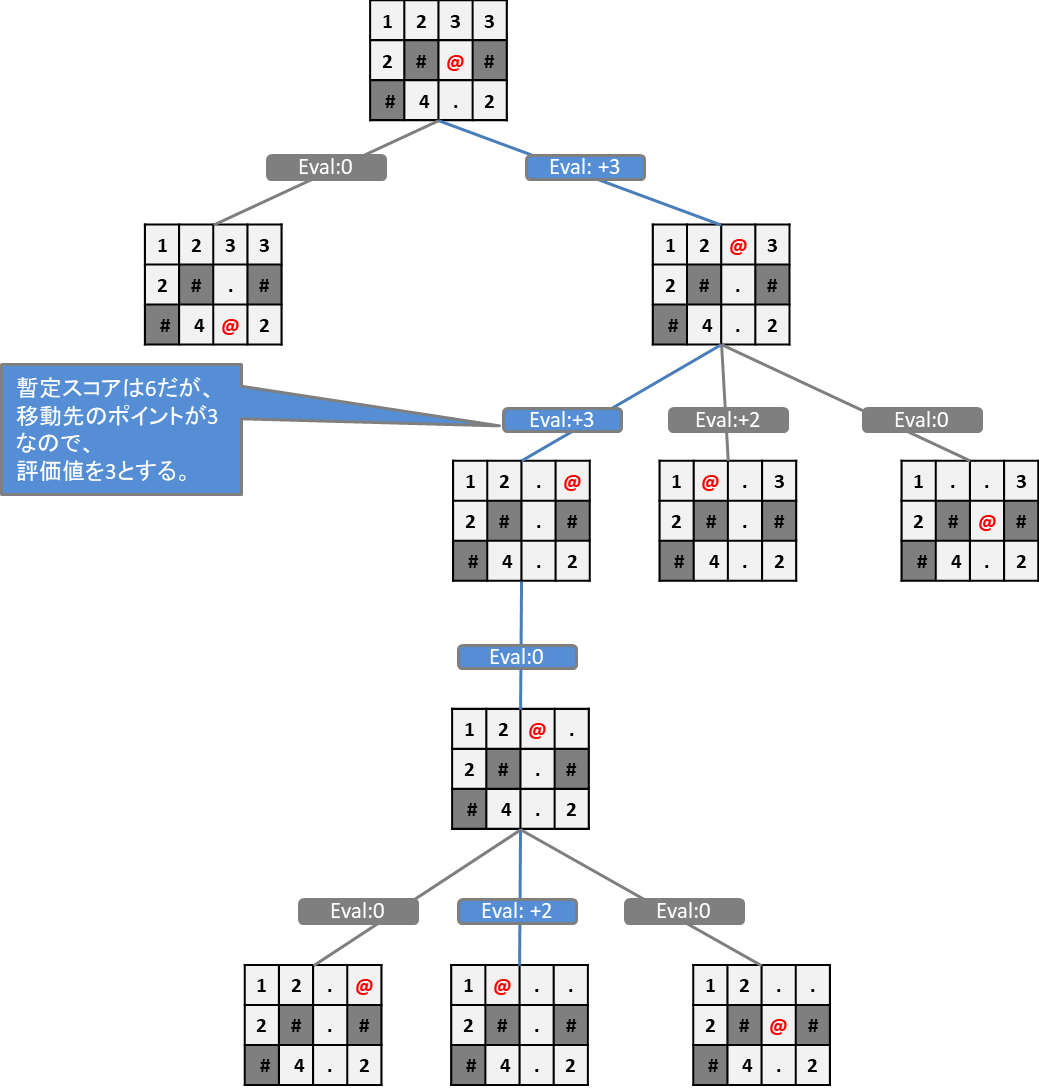
各ターンで取得した床のポイントを評価関数として貪欲法を適用した場合、以下のように
上移動(スコア+3)→右移動(スコア+3)→左移動(スコア+0)→左移動(スコア+2)
となります。(図中Evalは評価値)
つまり、先ほど説明したゲームスコアそのままの評価で貪欲法を適用した場合と同じ結果が得られました。
エッジを評価する方針で貪欲法を適用することで、一部の問題設定では計算時間の削減が期待できます。
そのため、貪欲法だけを意識した開発をしている場合、この方針でスコア計算をする場合もあるようです。
が、本記事で伝えたいことはこの方針のメリットではなくデメリットの方なので、詳細は省きます。
ビームサーチの評価関数設計を変えることによる結果の比較
貪欲法では、ノードを評価する方針でもエッジを評価する方針でも同じ結果が得られました。
では、ビームサーチで同様の比較をしてみましょう。
ノード(盤面)を評価する方針
ノードを評価する方針でビームサーチを行った場合、以下のように最終スコア9を得ることができます。
エッジ(遷移)を評価する方針
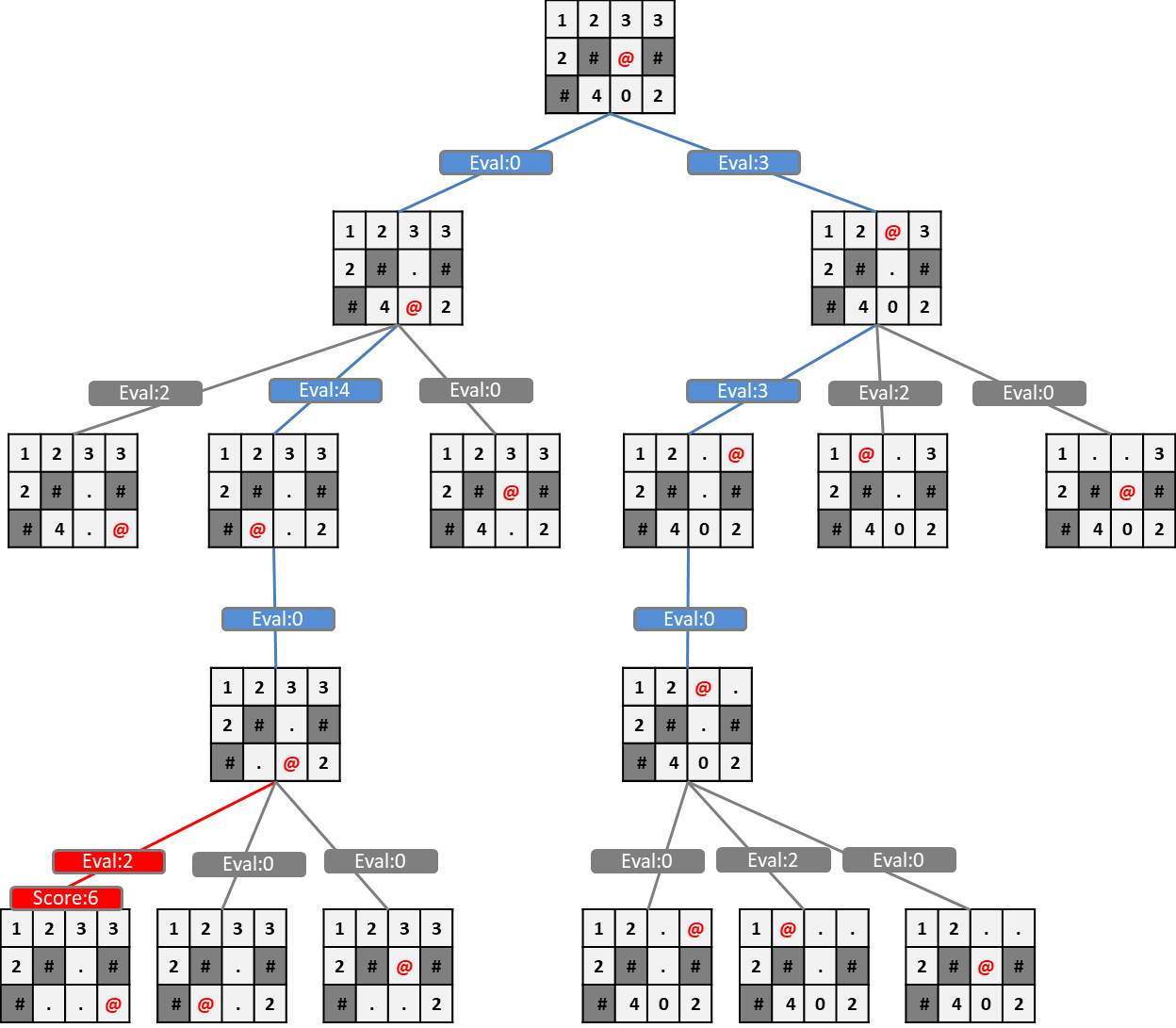
エッジを評価する方針でビームサーチを行った場合、以下のように最終スコア6となりました。
ノードを評価する方針よりも結果が悪くなったことがわかります。それどころか、貪欲法のスコア8よりも悪くなりました。
貪欲法よりも多くの空間を探索する手法であるビームサーチが、なぜ貪欲法でうまくいく評価関数で貪欲法よりも悪い結果となるのでしょうか。
貪欲法は1手先の状態だけを確認してよりよい方へと進む手法です。そのため、1手先でどの程度現在から改善されるかを評価することと、1手先の状態がどの程度良いかを評価することに違いはありません。
一方で、ビームサーチは、2手、3手先まで深く探索することで、将来の状態がより良い結果になることを期待する手法です。エッジを評価すると、n手先の状態からn+1手先の状態に遷移する際にどの程度改善するかを評価することになり、1手先からn手先でどの程度改善されるかが評価に反映されません。
そのため、最終結果が必ずしもいい方向に進むとは限りません。
まとめ
今回、「貪欲法だとうまくいくが、ビームサーチへの適用は望ましくない評価関数」について紹介しました。
結論としては、ビームサーチの評価関数は、「対象ノードがどの程度よいか」を表すように設計することが大事です。
貪欲法とビームサーチの挙動を正しく理解していれば、自然とこの考え方は身についてると思います。そのため、この記事で記載した内容をあえて読む必要はないかもしれません。
しかし、貪欲法に慣れ親しんで、自分なりに工夫していた方にとっては、いつもの方法で設計した評価関数がビームサーチではうまくいかない、といった場面があるかもしれません。
そうなるとどこを直すべきかわからなくなるかもしれないので、本記事が少しでもそういった方々の助けになればと思います。