はじめに
書籍化
本記事を元に
ゲームで学ぶ探索アルゴリズム実践入門~木探索とメタヒューリスティクス
という書籍を出版することになりました!
本記事を読んで気になっていただけたらご購入をご検討いただけるとうれしいです!
この記事で得られる技術
- ゲームルールに適した探索アルゴリズムを選択する
- ゲーム木探索をするのに適したクラス設計
- 主要なゲーム木探索アルゴリズムの実装
この記事の特徴
- 汎用アルゴリズムの実装例による他ゲームへの応用力と、実際に動作可能なサンプルコードによる具体的実装イメージの両視点でわかりやすくした(片方しか記載のない記事が多い)
- サンプルコード付き日本語記事がほぼないDUCTを解説している
- サンプルコードは印のついたメソッドを実装したクラスさえ書けば、アルゴリズム部分を変更せずそのまま他のゲームで動作可能になっている
この記事で扱わない関連技術
- 探索の高速化
- 多様性の確保
- 機械学習
この記事を書いたきっかけ
- 人にゲームAI教えたらけっこう楽しかった
- 周りの人々が技術書を出版しがちでうらやましいので、まずはハードルの低いQiitaで書いた。バズってえらい出版社の人の目にとまったらいいな。
サンプルコード置き場
本記事中にもサンプルコードを埋め込んでいますが、以下に実際に実行可能な一連の動作が確認できるサンプルコードを用意しています。
記事中に紹介していない、各アルゴリズムを時間いっぱい回すコードや、テストコードなども用意しているため、記事を読んだだけでわからない場合は、ぜひご利用ください。
https://github.com/thun-c/GameSearch
ゲーム木探索概要
ゲーム木探索とは
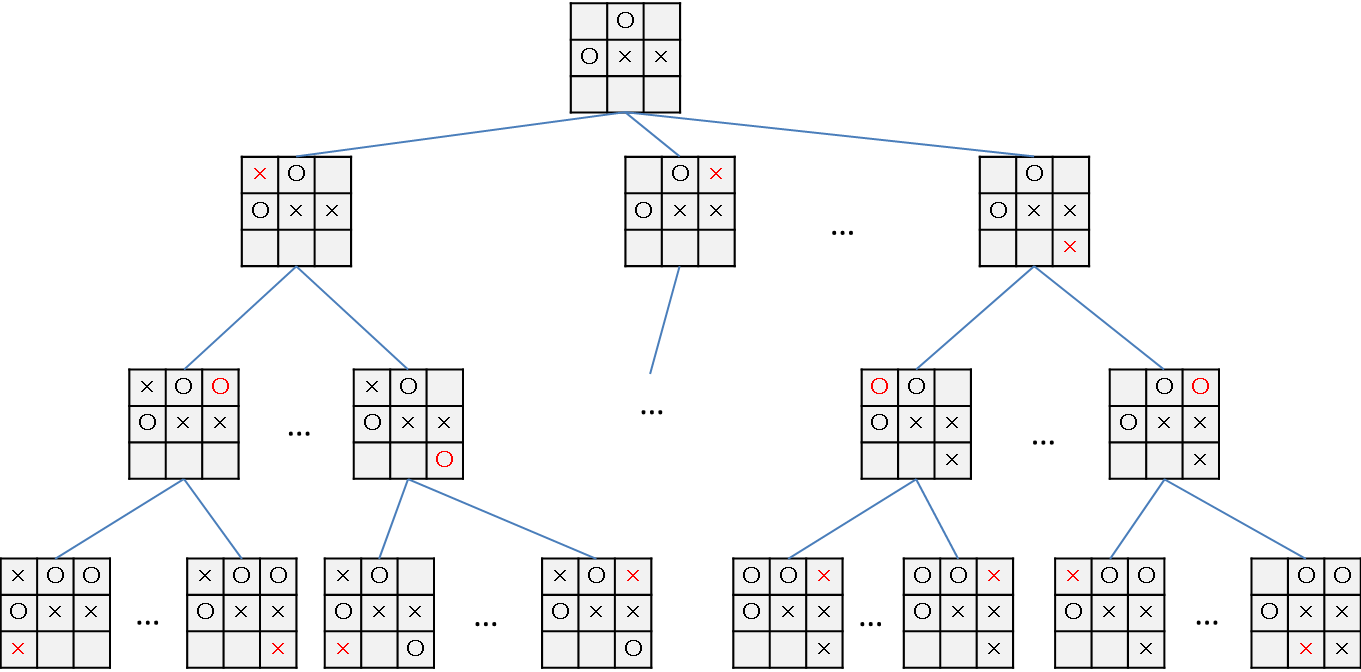
簡単に言うと、あるゲームで可能な行動をツリー上に表し、そのツリーをたどることでよりよい行動をとるための手段です。
…と言われてもピンとこないかと思いますので、
○×ゲームを例にとります。
上のような状況で、先手はどこに×を打つべきか考えます。
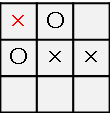
左上に×を打ってリーチをかけてみましょうか。
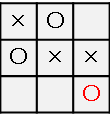
おや、○を置かれてリーチを防がれてしまいました。むむむ、、
では、最初に選ぶ行動を変えてみましょう。
左上ではなく右下に×をおいてみます。
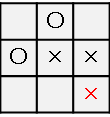
おやおや?リーチが二つあるので後手は左上か右上のどちらかを防いでももう片方を×がおいて×が勝利しそうです。
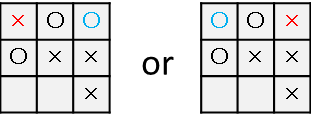
と、このように、将来起こり得ることを何パターンか予想すればよりよい行動ができそうです。
将来起こり得ることのパターンは以下のように表現してみます。
これをゲーム木と呼びます。
このゲーム木を特定の法則に沿って探索し、よりよい行動を見つる手法がゲーム木探索です。
(パターンが多すぎるので一部省略しています。)
用語と探索アルゴリズムの目的
ゲーム木を探索する際、各ターンで行動可能な手を合法手と呼びます。
木の横方向をどれぐらい探索するかを幅、
木の縦方向をどれぐらい探索するかを深さ
と呼びます。
仮に合法手の数nが固定のゲームを深さdまで探索しようとすると、最も深いところでは探索幅が$n^d$となり、これは深さ次第では現実的な時間で計算できなさそうです。
そこで、木全体をくまなく探索するのではなく、探索の幅や深さを制御することで、効率的に良い手を見つけるのが探索アルゴリズムの目的です。
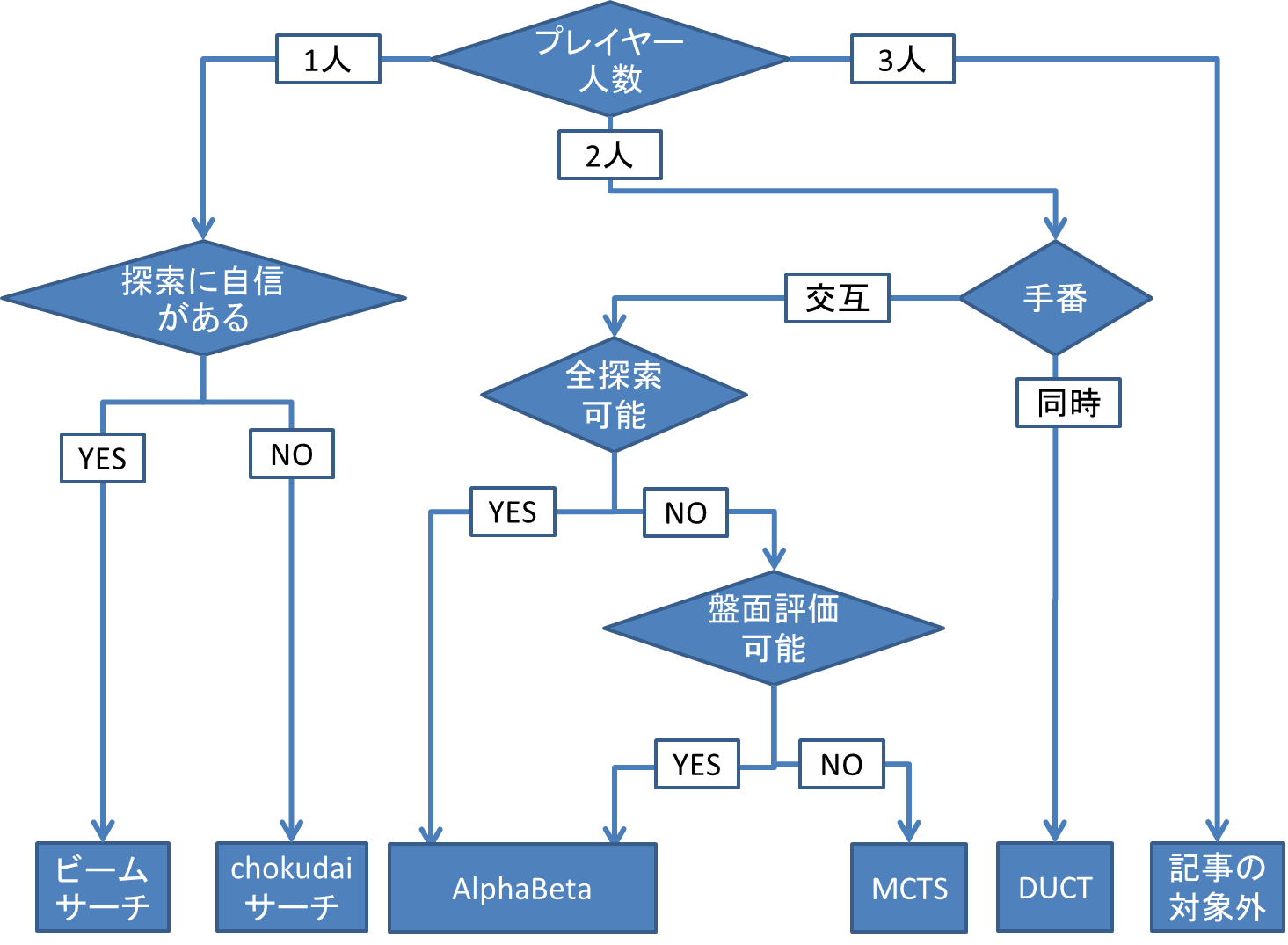
ゲームの種類と探索アルゴリズム
本記事で扱うゲームの種類とよく使う探索アルゴリズムを説明します。
- 一人ゲーム(or 疑似一人ゲーム)
プレイヤーが一人だけ、もしくはプレイヤーは複数人だが自分の環境に影響を与えられるプレイヤーがほぼ自分一人のゲーム
ゲーム例:ぷよぷよ、テトリス
アルゴリズム例:ビームサーチ、Chokudaiサーチ - 交互着手二人ゲーム
プレイヤーが二人で、交互に手番が回るゲーム
ゲーム例:○×ゲーム、将棋、
アルゴリズム例:MiniMax, AlphaBeta, MCTS - 同時着手二人ゲーム
プレイヤーが二人で、同時に手番が来るゲーム
ゲーム例:ボンバーマン
アルゴリズム例:DUCT
本当はゲームの分類はもっと細かい定義があるのですが、厳密に分類すると細分化されすぎるので雰囲気で読み取ってください。
ちょっとかじった人なら「二人零和有限確定完全情報ゲーム」か否かとかを気にしがちですが、あれを厳密に満たすゲームはそうそう存在しないです。(将棋、囲碁、チェスは有限ではないという解釈がある)
重要なのはゲームルールから解釈してどのアルゴリズムが(比較的)適しているかを判断することです。
上記と重複する部分もありますが、簡単にアルゴリズムの選択フローチャートを載せますので、ぜひ参考にしてみてください。
一人ゲームに使いたい探索アルゴリズム
ゲーム例:数字集め迷路
アルゴリズムを説明するにあたり、具体的にゲームを示して説明します。
ぷよぷよなどは連鎖が複雑なため、説明用オリジナルゲームをつくりました。
ゲームの目的:迷路を進みながら3ターン後の時点のスコアを高くする。
キャラクター(@)は、1ターンに上下左右四方向のいずれかに壁(#)のない場所に1マスずつ進む。
床にあるポイント(1~9)を踏むと自身のスコアとなり、床のポイントが消える。(.)

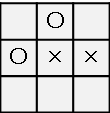
たとえば上のような初期盤面から「上、右、右」の順に進むと、
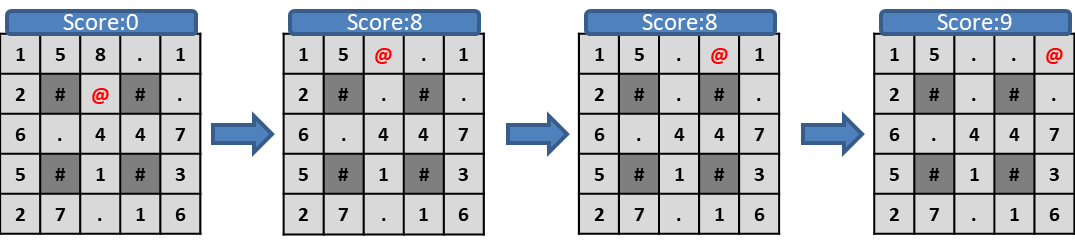
プレイヤーの最終スコアは9になります。
このスコアを最大化させるのが目的です。
一人ゲームのクラス設計
ゲームをクラスで実装しておくと、後で紹介する探索アルゴリズムが実装しやすいです。
以下のメソッドをゲームルールに沿って実装したクラスを用意すれば、例示したゲームでなくても後述の一人ゲーム用アルゴリズムのサンプルコードをそのまま利用可能です。
数字集め迷路の実装例はgithubに載せています。
Actionは行動を示す型です。ゲームの行動をどんな型で表すかも工夫の余地があるためActionという表記にしましたが、intと読み替えていただいていいです。
githubに載せたサンプルコードではusing Action = int; using Actions = std::vector<int>;としています。
class State {
public:
// 探索用の盤面評価をする
void evaluateScore();
// ゲームの終了判定
bool isDone()const ;
// 指定したactionでゲームを1ターン進める
void advance(const Action& action);
// 現在の状況でプレイヤーが可能な行動を全て取得する
Actions legalActions()const ;
};
// 探索時のソート用に評価を比較する
bool operator<(const State& state_1, const State& state_2);
貪欲法(Greedy)
1ターン後にあり得る盤面全てから評価が高い盤面になるように行動を決定する手法です。
実装が簡単かつ評価方法が上手ければ一定以上の効果が期待できる手法のため、他の手法を知っている人でもまずは貪欲法を試す人が多いです。

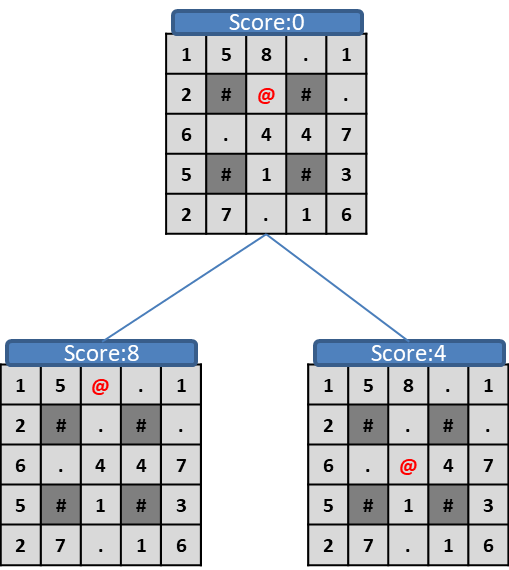
この盤面から深さ1の木をつくってみます。
左と右は壁(#)があって進めないため、上方向と下方向の2つが合法手です。
上はスコア8、下はスコア4のため、1ターン目は上方向に進むことを選択します。
この方法でゲームが3ターン後まで繰り返すと、3回の行動は「上、左、左」最終スコアが14
になります。
Action greedyAction(const State& state) {
auto legal_actions = state.legalActions();
ScoreType best_score = -INF;
Action best_action = -1;
for (const auto action : legal_actions) {
State now_state = state;
now_state.advance(action);
now_state.evaluateScore();
if (now_state.evaluated_score_ > best_score) {
best_score = now_state.evaluated_score_;
best_action = action;
}
}
return best_action;
}
ビームサーチ
探索幅を固定して探索する手法です。
例えば、探索幅を2の場合の流れを説明します。
まず、1ターン後にあり得る盤面全てを評価します。
合法手が3つで、それぞれの評価が5,1,3になった場合、このような木で表せます。
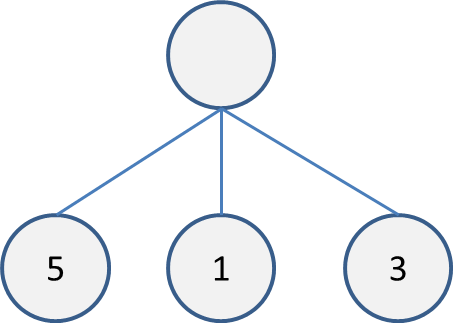
探索幅を2にした場合は、この中で評価が高い順に2つ選択して木を展開します。
この場合は5と3です。実装上は優先付きキューを使うか、まとめてソートをしてから2つを選びます。
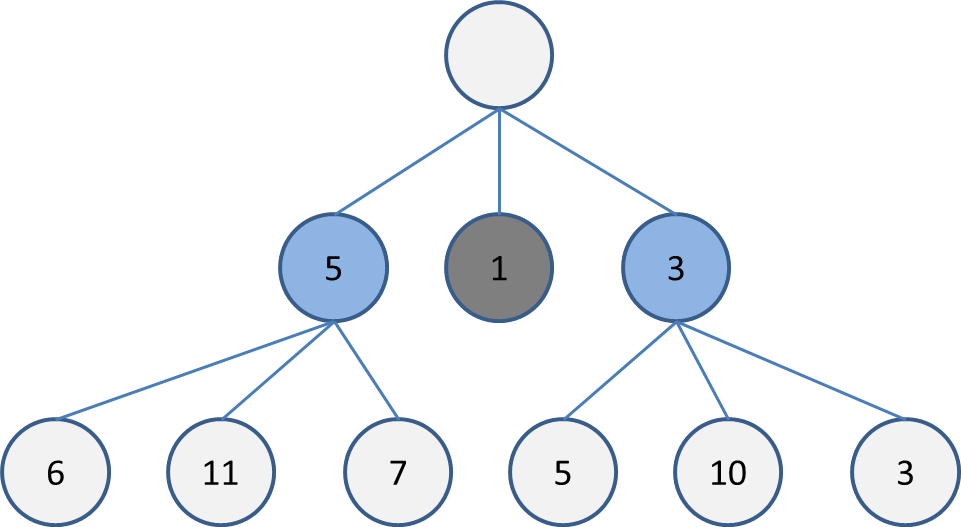
現状の最深部に6, 11, 7, 5, 10, 3があるので、この中で評価が高い11, 10を選択して木を展開します。
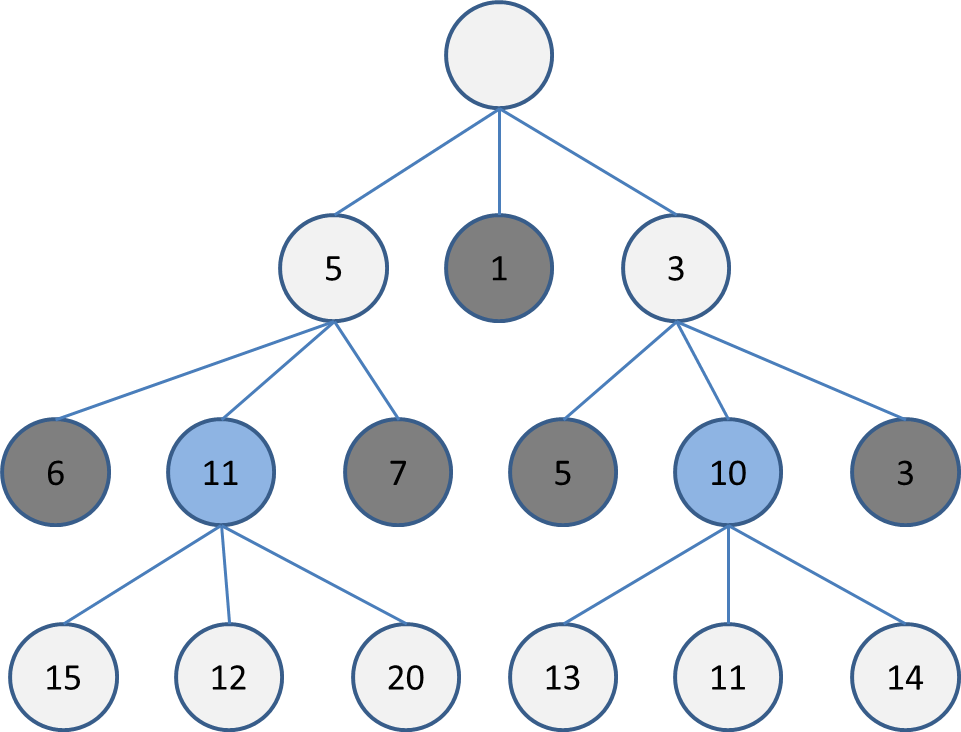
これを指定した深さ(or 時間)になるまで繰り返します。
Greedyよりも深い位置まで探索できるため、将来的なスコアがGreedyより高くなります。
// ビーム幅と深さを指定してビームサーチで行動を決定する
Action beamSearchAction(const State& state, const int beam_width, const int beam_depth) {
auto legal_actions = state.legalActions();
std::priority_queue<State> now_beam;
State best_state;
now_beam.push(state);
for (int t = 0; t < beam_depth; t++) {
std::priority_queue<State> next_beam;
for (int i = 0; i < beam_width; i++) {
if (now_beam.empty())break;
State now_state = now_beam.top(); now_beam.pop();
auto legal_actions = now_state.legalActions();
for (const auto& action : legal_actions) {
State next_state = now_state;
next_state.advance(action);
next_state.evaluateScore();
if (t == 0)next_state.first_action_ = action;
next_beam.push(next_state);
}
}
now_beam = next_beam;
best_state = now_beam.top();
if (best_state.isDone())
{
break;
}
}
return best_state.first_action_;
}
Githubには指定した時間いっぱいまで深く探索するコードも載せています。
Chokudaiサーチ
計算過程の評価を覚えながら極細(幅1など)ビームサーチを繰り返す手法です。
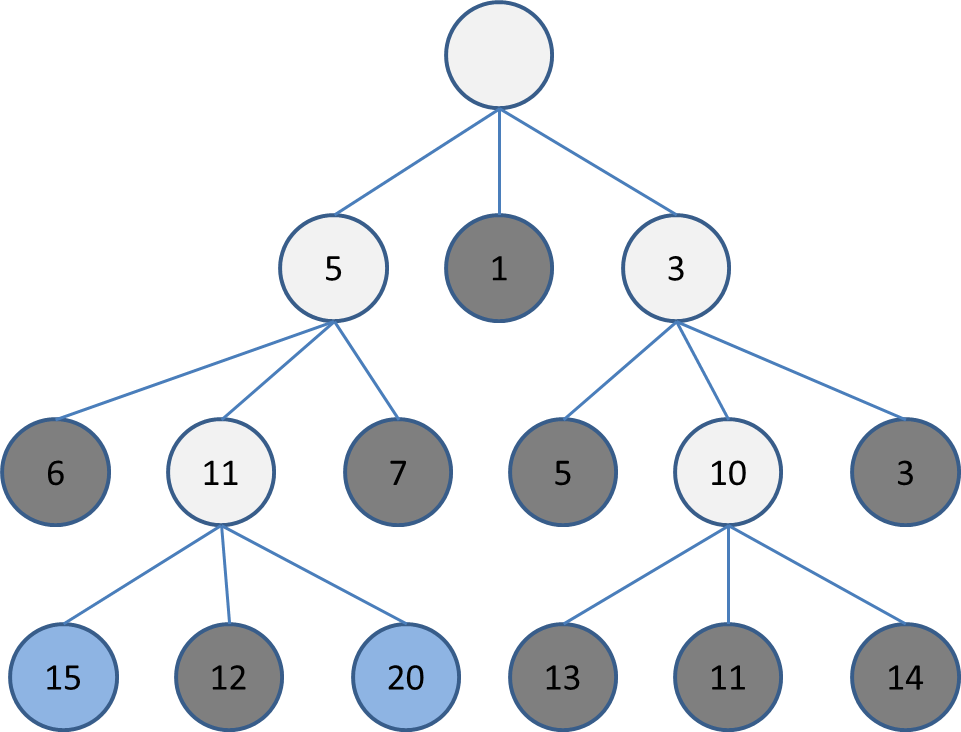
これはビーサーチの説明で使った木の続きです。深さ3の段階で次に探索するのは幅2なら20と15ですね。
ここで、20と15は木の根本をたどると同じですね。
探索の目的は、木の根元でどの行動をとるかを選択することです。
根本が同じ盤面をどれだけ探索してもよい行動の選択にはつながらないです。
このように、根本が同じ盤面ばかり探索してしまう状態を「多様性がない」と言います。
逆に、根本がばらけた探索ができている状態は「多様性がある」と言います。
せっかく深くまで探索するのですから、なるべく似てない盤面を探索して深い探索の意味があるようにしたいです。
ビームサーチの場合はこの多様性の確保のための工夫を自分で考える必要があるので、初心者には少し難しいです。
そこで、一度深い位置まで探索しても浅い位置からまた探索をやりなおしていけば多様性を確保しながら深い探索をできるというのがChokudaiサーチです。
まず、幅の狭い(例は幅1)ビームサーチを1回します。
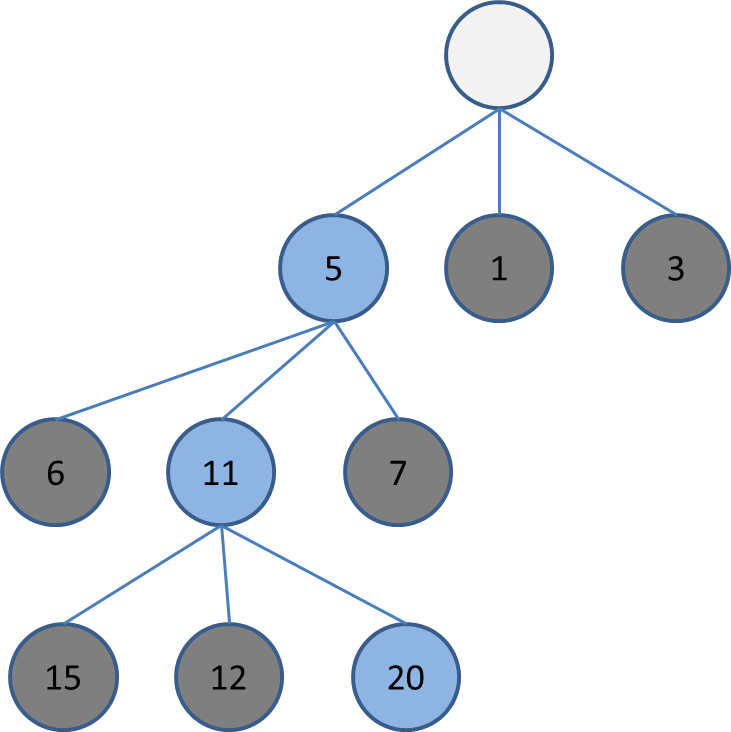
この時、選択しなかった盤面の評価も全て覚えておきます。
その後、深さ0からまた同じ幅のビームサーチをします。
この時、2回目以降のビームサーチでは、各深さでまだ選択されていない盤面を選ぶようにします。
そうすると、2回目のビームはこのようになります。
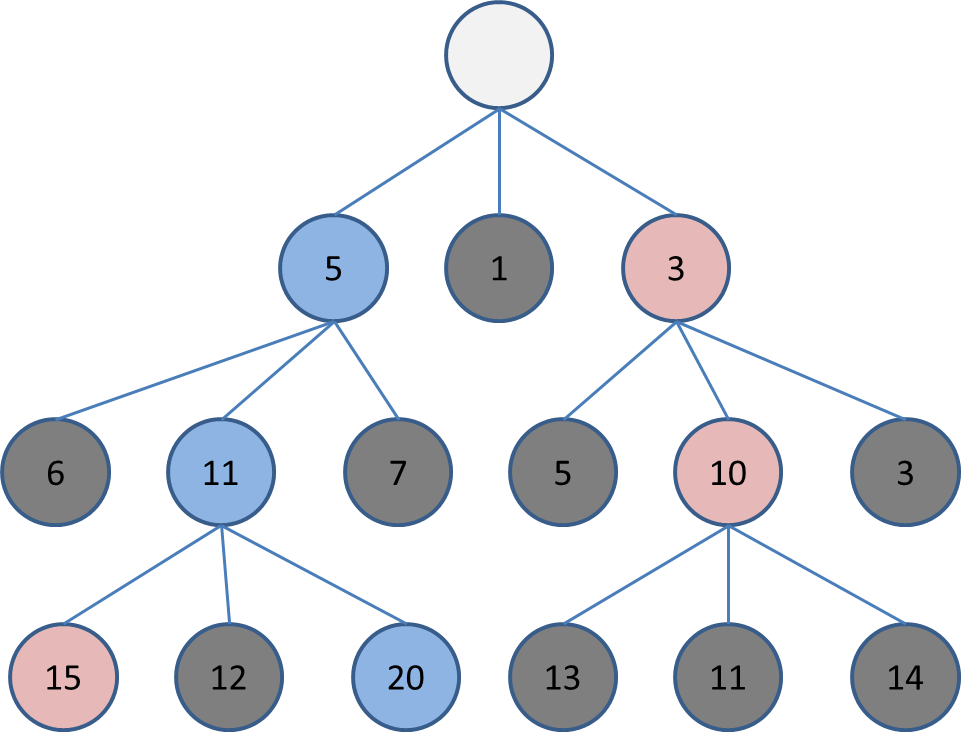
このままだと深さ3で選択した盤面が20と15なので幅2のビームサーチをした時と同じです。
ここで3回目のビームサーチをします。
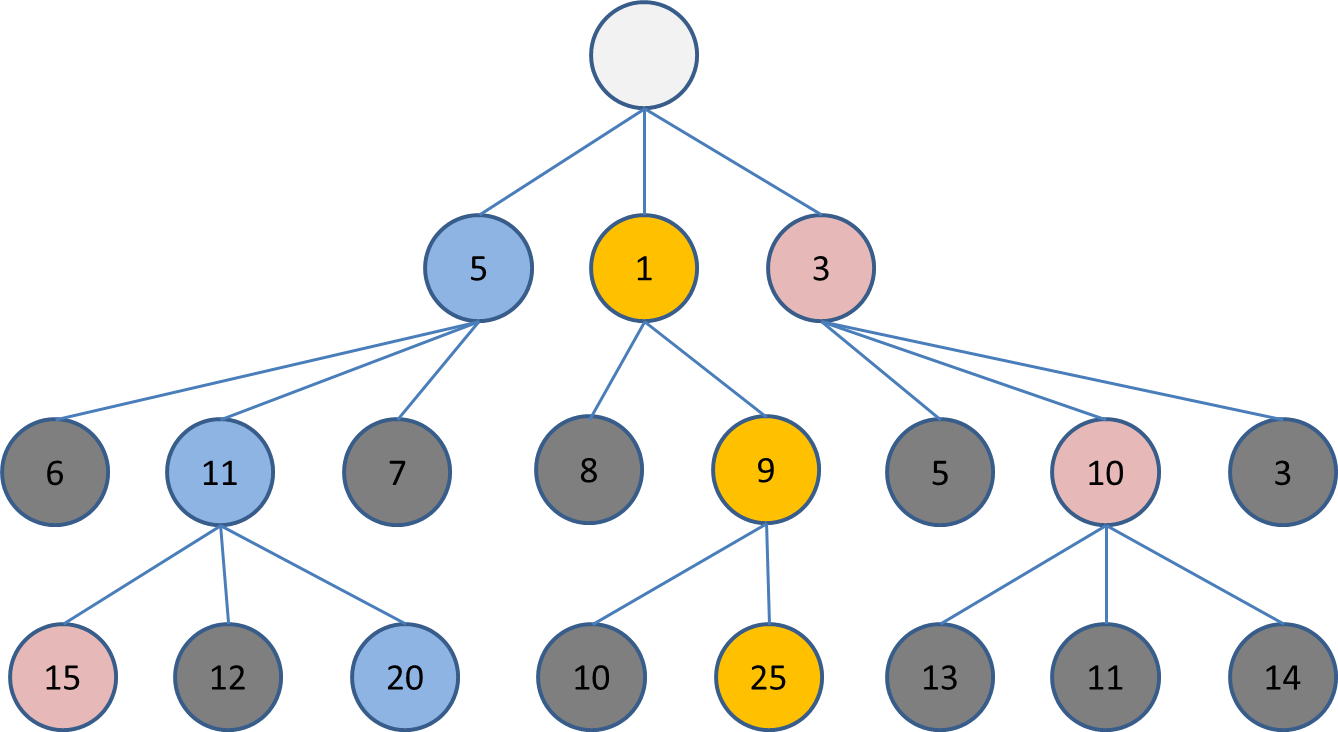
深さ1では低評価の1だった盤面から進んだ盤面が、深い探索では実は高い評価になることが判明しました。
深さ4以上の探索についても、根本の違う盤面を評価できるようになり、多様性が確保された探索ができるはずです。
このように、多様性を簡単に確保できる点で、Chokudaiサーチは初心者の方にオススメの探索といえます。
なお、Chokudaiサーチ考案者のブログにはビームサーチをしっかりチューニングできるならChokudaiサーチは不要との見解が記載されています。
自分の力量や目的と相談しながらビームサーチと使い分けるとよいでしょう。
ちなみに、Chokudaiサーチはビームスタックサーチであると勘違いされることが多いのですが、ビームスタックサーチではないという報告もあるようです。
// ビーム1本あたりのビーム幅とビームの本数を指定してchokudaiサーチで行動を決定する
Action chokudaiSearchAction(const State& state, const int beam_width, const int beam_depth, const int beam_number) {
auto beam = std::vector<std::priority_queue<State>>(beam_depth + 1);
for (int t = 0; t < beam_depth + 1; t++) {
beam[t] = std::priority_queue<State>();
}
beam[0].push(state);
for (int cnt = 0; cnt < beam_number; cnt++) {
for (int t = 0; t < beam_depth; t++) {
auto& now_beam = beam[t];
auto& next_beam = beam[t + 1];
for (int i = 0; i < beam_width; i++) {
if (now_beam.empty())break;
State now_state = now_beam.top();
if (now_state.isDone()) {
break;
}
now_beam.pop();
auto legal_actions = now_state.legalActions();
for (const auto& action : legal_actions) {
State next_state = now_state;
next_state.advance(action);
next_state.evaluateScore();
if (t == 0)next_state.first_action_ = action;
next_beam.push(next_state);
}
}
}
}
for (int t = beam_depth; t >= 0; t--) {
const auto& now_beam = beam[t];
if (!now_beam.empty()) {
return now_beam.top().first_action_;
}
}
return -1;
}
Githubには指定した時間いっぱいまで深く探索するコードも載せています。
交互着手二人ゲームに使いたい探索アルゴリズム
ゲーム例:○×ゲーム(三目並べ)
ゲーム木探索の説明にも使いましたが、交互着手二人ゲームの説明には○×ゲームを使います。
ゲームの目的:自分の駒を縦、横、斜めの四方向いずれかで3つ揃えること
プレイヤーは二人で、交互に3×3のマス目のどこかに自分の駒を置く。
どちらかの駒が3つ揃うか、置けるマスがなくなった時点で終了。
終了時点でどちらも勝利条件を満たしていない場合は引き分け。
交互着手二人ゲームのクラス設計
例のごとく、○×ゲームの実装例はgithubに載せています。
class State {
public:
// 現在のプレイヤー視点の盤面評価をする
ScoreType getScore()const;
// 現在のプレイヤーが負けたか判定する
bool isLose()const;
// 引き分けになったか判定する
bool isDraw()const;
// ゲームが終了したか判定する
bool isDone()const;
// 指定したactionでゲームを1ターン進め、次のプレイヤー視点の盤面にする
void advance(const Action action);
// 現在のプレイヤーが可能な行動を全て取得する
Actions legalActions()const;
};
MiniMax
交互着手ゲームでは、一人ゲームと違って相手の行動の影響を強く受けます。
○×ゲームで自分の駒を3つそろえることだけ考えてリーチをかけたら、相手が邪魔をしてきて負けてしまった、なんてこともあるんじゃないでしょうか。
そこで、自分も相手も最善手を打ち続けるという前提のもとにシミュレーションし、現状の最善手を打とうという手法がMiniMaxです。
たとえば、ゲーム終了時点の評価を「勝利:1, 負け:-1, 引き分け:0」としてある盤面からの木を生成します。
今は×の手番だとします。
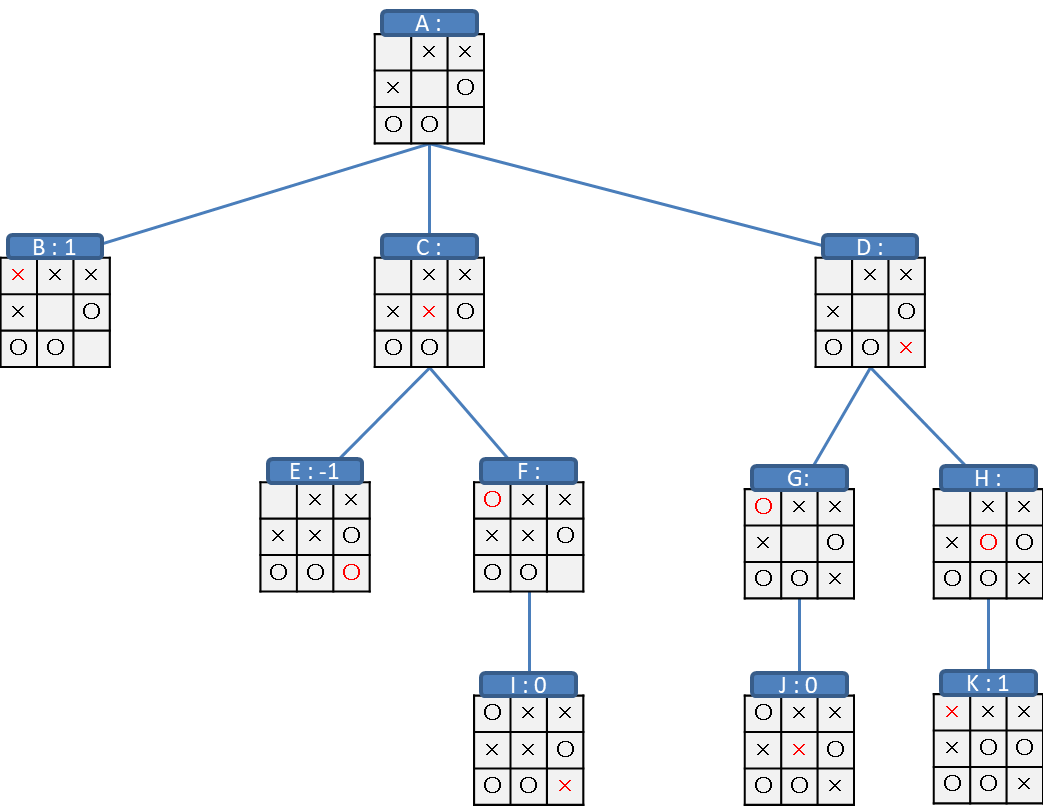
そうすると、B、Kの盤面は×がそろって勝ったので評価1、Eの盤面は○がそろって負けたので評価-1、I、Jの盤面はどちらもそろわずに盤面が埋まったので評価0です。
これで木の最も深い位置の評価が全て決まりました。
それぞれ根本にむかって浅い位置の盤面の評価をしていきます。
F,G,Hからは分岐がないため、そのままI,J,Kの評価を利用できるので、
AやCのように分岐がある場合を考えます。
それぞれの盤面では、手番が自分の場合は進める盤面の中で評価が最大のものを、手番が相手の場合は進める盤面の中で評価が最小のものを選びます。
交互着手ゲームの場合は手番が自分、敵、自分、と交互に進むため、単純に木の深さが偶数か奇数かで考えればよいです。
ここで、Cから進める盤面はE(-1)とF(0)の二つで、相手の手番のため、小さいほうの-1をCの評価とします。
同様に、Dの評価はG:(0)とH(1)の小さいほうの0となります。
Aの盤面は自分の手番のため、B(1),C(-1),D(0)の中で最大である、B(1)を選択します。
なお、○×ゲームは探索木が小さいため、最後まで探索するのが簡単ですが、実際にはゲームが終了するまで探索することは難しいです。
そのような場合は途中の盤面でも評価を決めて、現実的な深さまで探索することで、最善とまではいかないまでも、それなりに良い手を指すことができます。
サンプルコードでは深さを指定可能なように実装しているので、ぜひ参考にしていみてください。
なお、聡明な読者様ならお気づきかもしれませんが、先述の交互着手二人ゲームのクラス設計にて、void advance(const Action action);のコメントに「次のプレイヤー視点の盤面にする」と記載しています。
実は、交互着手ゲームで探索をする時は常にその手番のプレイヤー視点の盤面になる実装をすることで、「最大値の評価と最小値の評価を交互に繰り返す」処理を「常に最大値の評価をする」コードで簡単に実装できるようになります。
MiniMaxをこのテクニックで実装することをNegaMaxと呼びます。
// minimaxのためのスコア計算
ScoreType miniMaxScore(const State& state, const int depth) {
if (state.isDone() || depth == 0) {
return state.getScore();
}
auto legal_actions = state.legalActions();
if (legal_actions.empty()) {
return state.getScore();
}
ScoreType bestScore = -INF;
for (const auto action : legal_actions) {
State next_state = state;
next_state.advance(action);
ScoreType score = -miniMaxScore(next_state, depth - 1);
if (score > bestScore) {
bestScore = score;
}
}
return bestScore;
}
// 深さを指定してminimaxで行動を決定する
Action miniMaxAction(const State& state, const int depth) {
ScoreType best_action = -1;
ScoreType best_score = -INF;
for (const auto action : state.legalActions()) {
State next_state = state;
next_state.advance(action);
ScoreType score = -miniMaxScore(next_state, depth);
if (score > best_score) {
best_action = action;
best_score = score;
}
}
return best_action;
}
AlphaBeta
MiniMaxは合法手全てを探索することになるため、探索する深さに応じて指数的に探索時間が伸びてしまいます。
実は、MiniMaxと全く同じ結果を出すことを保証しつつ探索時間を大幅に削減する方法があるので紹介します。
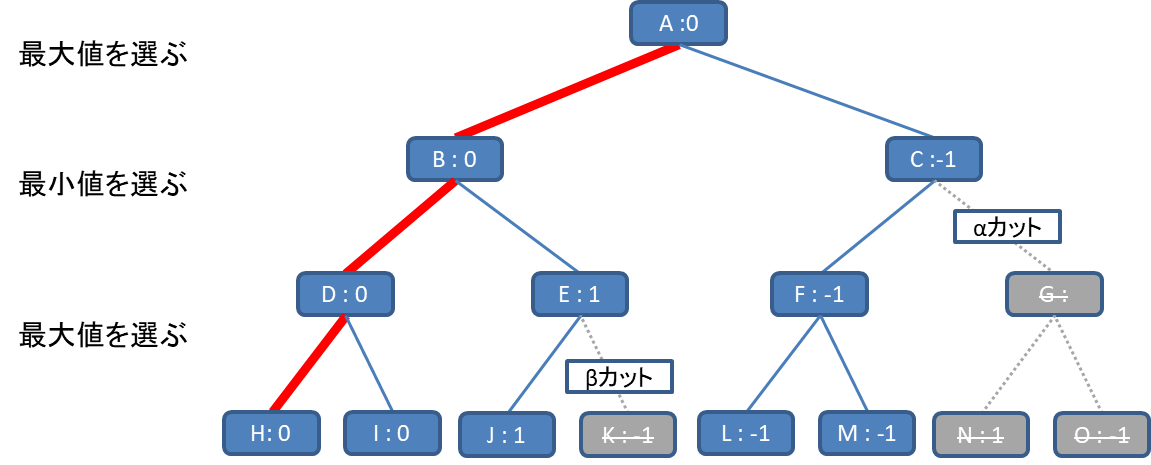
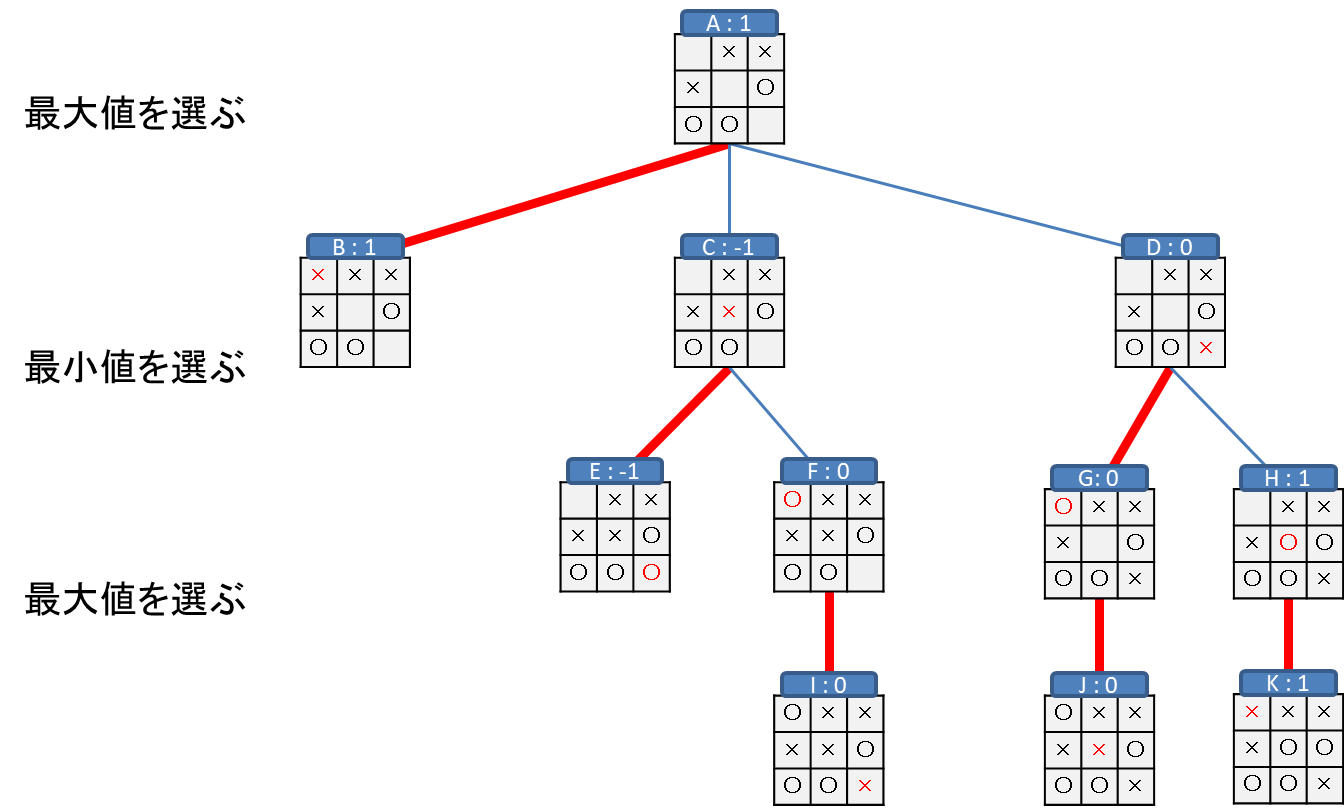
とある盤面Aから深さ3の木を考えます。
まずはH,Iの盤面の評価が0なので、Dの評価が0に決まります。ここまでは通常のMiniMaxと同じです。
ここで、Jの探索まで進んだ段階で、Jの評価が1でした。通常のMiniMaxならばKも評価した時点でEの評価を決定できるはずですが、EはJとKの最大値のはずです。
つまり、EはJの値(1)が決まった時点でKの値に限らず1以上であることが確定します。
ここで、Eが1以上ということはDの評価値の0よりも大きいことが確定します。そうすると、BはDとEのうち最小のものが評価になるため、Eより小さいことが確定しているDの0がBの評価値となります。
Bの評価値が確定したので、Kの評価はもうしなくてよいです。
このように、ある評価がある値以上になることで、探索を打ち切ることを「βカット」と呼びます。
次に、LとMを評価からFの評価が-1と決まります。
Cの評価はFとGの最小値のはずなので、Cが-1以下であることが確定します。
この時点で、-1は0より小さいのでCよりBの方が大きいことが確定します。
Aの評価はBとCの最大値のため、Bの評価値である0だと確定します。
この時点で、G,N,Oの探索は不要になります。
このように、ある評価がある値以下になることで、探索を打ち切ることを「αカット」と呼びます。
このように「αカット」と「βカット」を繰り返すことで探索を打ち切って高速化することをAlphaBeta法と呼びます。
// AlphaBetaのためのスコア計算
ScoreType alphaBetaScore(const State& state, ScoreType alpha, const ScoreType beta, const int depth) {
if (state.isDone() || depth == 0) {
return state.getScore();
}
auto legal_actions = state.legalActions();
if (legal_actions.empty()) {
return state.getScore();
}
for (const auto action : legal_actions) {
State next_state = state;
next_state.advance(action);
ScoreType score = -alphaBetaScore(next_state, -beta, -alpha, depth - 1);
if (score > alpha) {
alpha = score;
}
if (alpha >= beta) {
return alpha;
}
}
return alpha;
}
// 深さを指定してalphabetaで行動を決定する
Action alphaBetaAction(const State& state, const int depth) {
ScoreType best_action = -1;
ScoreType alpha = -INF;
for (const auto action : state.legalActions()) {
State next_state = state;
next_state.advance(action);
ScoreType score = -alphaBetaScore(next_state, -INF, -alpha, depth);
if (score > alpha) {
best_action = action;
alpha = score;
}
}
assert(best_action >= 0);
return best_action;
}
Iterative Deepning(反復深化)
AlphaBeta法は深さを固定して探索する手法ですが、実用的には探索したい時間が決まっていることが多いです。
そこで、時間いっぱいまで探索をすることを考えます。
これは単純な話で、深さ1のAlphaBeta法を行い、時間が余ったら深さ2のAlphaBeta法を行う、を時間いっぱいになるまで深めて繰り返すだけです。
深さNのAlphaBetaをした時点で深さN-1以下の浅い探索は無駄になりそうですが、深さに応じて探索時間は指数的に伸びるため、浅い探索をしたことで生じる無駄な時間は無視してよいほど少ないです。
ちなみに、浅い探索の結果を深い探索の効率化に利用する方法などもありますが、AlphaBeta法を効率化するテクニックの話をし始めるとこの記事の文字数がとんでもないことになるため、割愛します。
// 時間を管理するクラス
class TimeKeeper {
private:
std::chrono::high_resolution_clock::time_point start_time_;
int64_t time_threshold_;
public:
// 時間制限をミリ秒単位で指定してインスタンスをつくる。
TimeKeeper(const int64_t& time_threshold)
:start_time_(std::chrono::high_resolution_clock::now()),
time_threshold_(time_threshold)
{
}
// インスタンス生成した時から指定した時間制限を超過したか判定する。
bool isTimeOver() const {
auto diff = std::chrono::high_resolution_clock::now() - this->start_time_;
return std::chrono::duration_cast<std::chrono::milliseconds>(diff).count() >= time_threshold_;
}
};
// 制限時間が切れた際に停止できるalphabetaのためのスコア計算
ScoreType alphaBetaScore(const State& state, ScoreType alpha, const ScoreType beta, const int depth, const TimeKeeper& time_keeper) {
if (time_keeper.isTimeOver())return 0;
if (state.isDone() || depth == 0) {
return state.getScore();
}
auto legal_actions = state.legalActions();
if (legal_actions.empty()) {
return state.getScore();
}
for (const auto action : legal_actions) {
State next_state = state;
next_state.advance(action);
ScoreType score = -alphaBetaScore(next_state, -beta, -alpha, depth - 1, time_keeper);
if (time_keeper.isTimeOver())return 0;
if (score > alpha) {
alpha = score;
}
if (alpha >= beta) {
return alpha;
}
}
return alpha;
}
// 深さと制限時間(ms)を指定してalphabetaで行動を決定する
Action alphaBetaActionWithTimeThreshold(const State& state, const int depth, const TimeKeeper& time_keeper) {
ScoreType best_action = -1;
ScoreType alpha = -INF;
for (const auto action : state.legalActions()) {
State next_state = state;
next_state.advance(action);
ScoreType score = -alphaBetaScore(next_state, -INF, -alpha, depth, time_keeper);
if (time_keeper.isTimeOver())return 0;
if (score > alpha) {
best_action = action;
alpha = score;
}
}
return best_action;
}
// 制限時間(ms)を指定して反復深化で行動を決定する
Action iterativeDeepningAction(const State& state, const int64_t time_threshold) {
auto time_keeper = TimeKeeper(time_threshold);
Action best_action = -1;
for (int depth = 1;; depth++) {
Action action = alphaBetaActionWithTimeThreshold(state, depth, time_keeper);
if (time_keeper.isTimeOver()) {
break;
}
else {
best_action = action;
}
}
return best_action;
}
原始モンテカルロ法
ここまで、交互着手ゲームについてはMiniMaxを軸とした手法の説明をしてきましたが、ここからガラッと考え方の変わる手法を紹介していきます。
情報系の大学出身の方なら「モンテカルロ法」は聞いたことあるんじゃないでしょうか。
そう、ランダムになんらかの試行を繰り返すことで近似解を求める手法の総称です。
大学で円周率を求める例だけ習って「モンテカルロ法って円周率を求める手法なんでしょ!知ってる!」なんて方がいたらちょっと反省してください。
乱数使って近似解を求めていたらなんでもモンテカルロ法を名乗ることができるのです。
さて、脱線してしまいましたが、ゲームにおいてどのようにモンテカルロ法を適用させるのか説明していきます。
まず、現在の局面からゲーム終了までシミュレーションすることをプレイアウト、ランダムな行動だけでプレイアウトをすることをランダムプレイアウトと呼びます。
まず、ランダムプレイアウトを1回します。
この時、1手目でどの行動をとったかと勝敗を確認します。
もし勝ちだったら「1回プレイアウトして1回勝った」ということを記録します。
これをひたすら繰り返すと、
「10回プレイアウトして6回勝った」行動Aは勝率が60%、
「12回プレイアウトして3回勝った」行動Bは勝率が25%、
のように、各行動の勝率を比較できます。
気が済むまでランダムプレイアウトを繰り返し、最も勝率が高い行動を選びます。
このような手順で行動を選択することを原始モンテカルロ法と呼びます。
MiniMax系の探索と違い、合法手の多いゲームでも、深さを途中で切らなくても、1回のプレイアウトを行うぶんには1通りの道筋しか通らないため、ゲームの勝敗での評価が確実にできるという点、自分で評価を考える必要がないので客観的な評価ができます。
// ランダムプレイアウトをして勝敗スコアを計算する
double playout(State* state) { // const&にすると再帰中にディープコピーが必要になるため、高速化のためポインタにする。(constでない参照でも可)
if (state->isLose())
return 0;
if (state->isDraw())
return 0.5;
state->advance(randomAction(*state));
return 1. - playout(state);
}
// プレイアウト回数を指定して原始モンテカルロ法で行動を決定する
Action primitiveMontecarloAction(const State& state, int playout_number) {
auto legal_actions = state.legalActions();
double best_value = -INF;
int best_i = -1;
for (int i = 0; i < legal_actions.size(); i++) {
double value = 0;
for (int j = 0; j < playout_number; j++) {
State next_state = state;
next_state.advance(legal_actions[i]);
value += 1. - playout(&next_state);
}
if (value > best_value) {
best_i = i;
best_value = value;
}
}
return legal_actions[best_i];
}
Githubには指定した時間いっぱいまで深く探索するコードも載せています。
MCTS(モンテカルロ木探索)
一見すると原始モンテカルロ法は試行回数を増やせば増やすほど行動の評価が正確になっていくように見えますが、実はそうでもないです。
というのも、自分の一手目以外は評価をしないため、相手が確実に勝てる状態にもかかわらず別の行動をとってくる、といった不可思議な手を打つこともシミュレーションしてしまいます。
そうすると、一見勝率が高いように見える手が実は相手の行動次第では負けが確定している、なんてこともあったりします。
そこで、自分も相手も、より深く探索している段階でもよさそうな手を打つようにしながら探索していきたいです。
そのための工夫として選択と展開を行います。
ここまでなるべく用語がないほうがいいかと思ってノードという言葉を使わず説明してきたのですが、さすがに無理がありました。
木の中でそれぞれの盤面を指す部分をノード、木の一番上にあるノードをルートノード、あるノードから1つ進んだ先にあるノードを子ノード、子ノードのないノードをリーフノードと呼びます。
まず、原始モンテカルロ法同様に深さ1のノードについて勝敗と探索した回数を記録していきます。
1回あたりのプレイアウトの勝敗によって得た評価を勝ち : 1, 引き分け : 0.5, 負け : 0として、今までのプレイアウトの評価の合計をw (累計価値)、プレイアウトした回数をn (試行回数)として記録します。
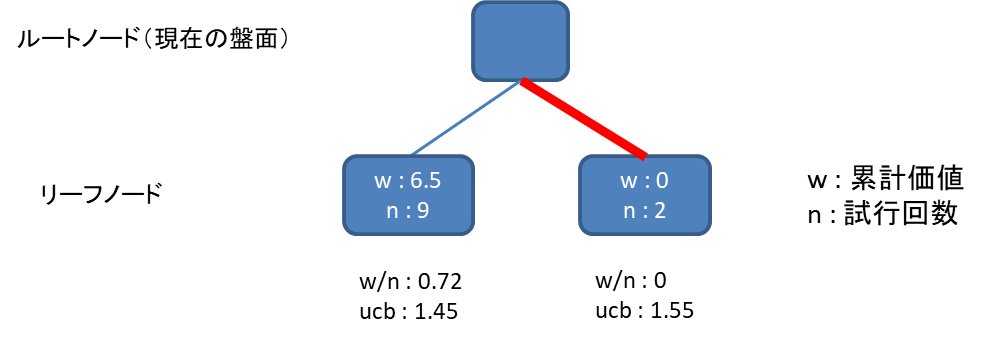
原始モンテカルロ法はランダムに行動を選択することが欠点だという話をしました。
では、どのように行動を選択するべきかなんですが、なるべく勝率のよいノードを選択すればそれらしい動きになりそうです。
上図の場合、勝率はw/nを計算すればよいので、左のノード(0.72)は右のノード(0)より勝率が高く、左のノードを選びたい気持ちになります。
しかし、左のノードはn=9のため、既に9回も選択しているようです。
勝率がいいからといっていつまでも左のノードばかり探索していては、右のノードの勝率が正確に測れません。
そこで、「どれぐらい探索していないか」という指標を用意し、その指標と勝率のバランスをとった上でどちらのノードを選ぶか決めることにします。
$$ UCB1 = \frac{w}{n} + C\sqrt{\frac{2ln(t)}{n}} \qquad※ln(t)=log_e(t)$$
勝率を示す$ \frac{w}{n} $とバイアス(探索してない度合い)を示す$ \sqrt{\frac{2ln(t)}{n}} $を重み$ C $付きで足しています。tは全子ノードの試行回数の総和です。
この指標を比較することで、バランスのよい探索が可能となります。なお、定数$ C $の値の決め方にルールはないため、どれぐらいバイアスを重視したいかを自分で考えてみてください。文献によってはC=1で固定されていることもあります。
上図では右のノードの方がucb1の値が高いため、右のノードを選択してプレイアウトをします。
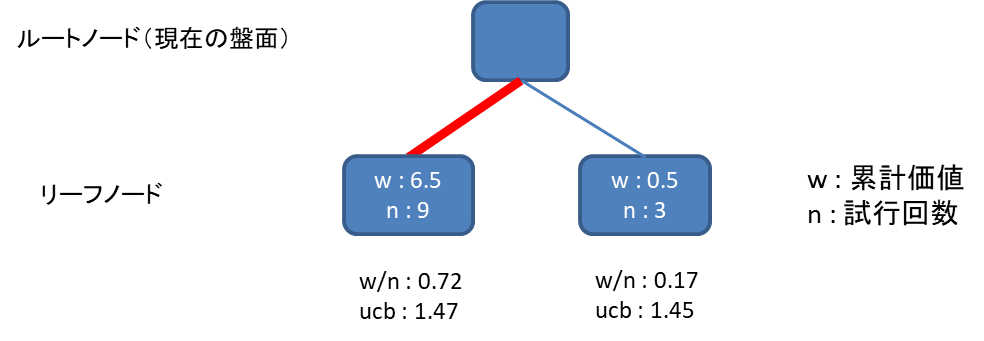
先ほどの図で右のノードからプレイアウトした結果、引き分けだったとします。
そうすると右のノードがw=0+0.5=0.5, n=2+1=3 となりました。
この時点でucb1を計算すると、左のノードの方が高くなるため、今度は左のノードを選択することになります。
さて、左のノードは既に9回も探索しているので、これで10回目になります。
ここで展開の説明をします。
いつまでも一手目の記録をつけていても、相手の行動を考慮できてないという欠点は変わりません。
そこで、試行回数が閾値を超えたノードについては、1手先の合法手で進められる全てのノードを追加します。
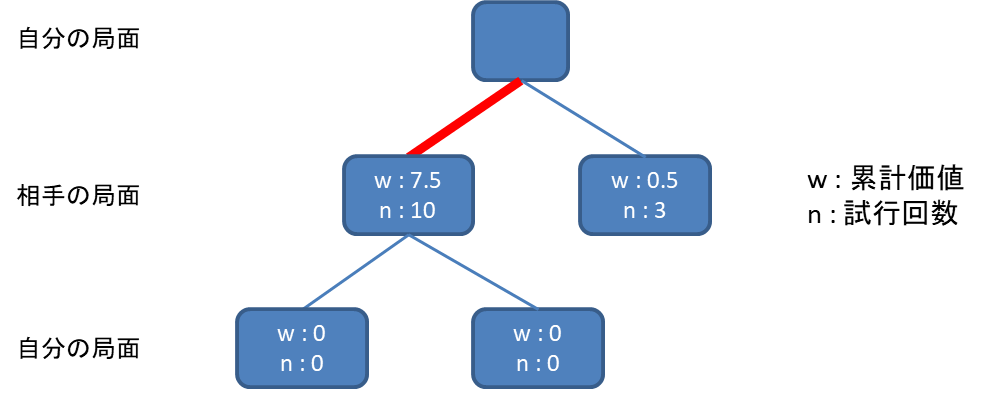
追加したノードはw,n,それぞれ0で初期化します。
今後、選択したノードに子ノードがある場合は、子ノードに対して選択を繰り返し、リーフノードに達した時点でプレイアウトするようにします。
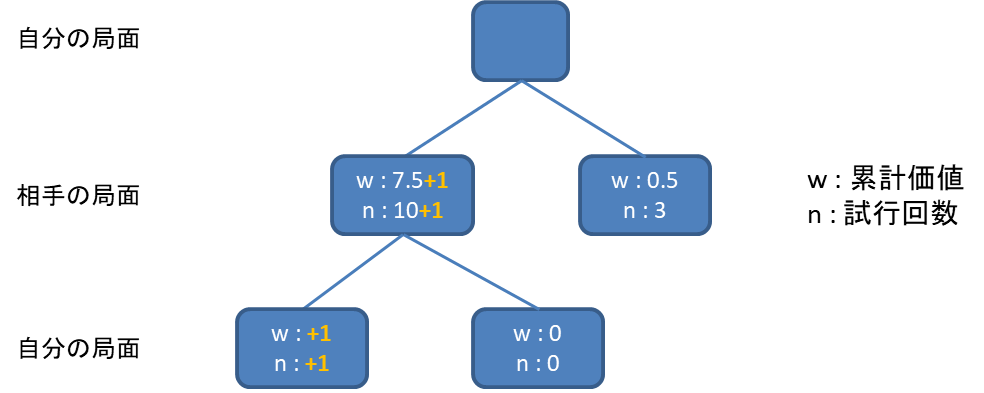
プレイアウトしたリーフノードの価値と試行回数は、そのまま親ノードに加算するようにします。
これで相手の局面でも選択が入るようになり、今後ノードの展開が進めば自分も相手も深いノードでの探索が可能となります。
そうすると、自分も相手もより賢い行動をしたシミュレーションができるため、原始モンテカルロ法と違って試行回数が増えるほどに評価した累計価値が洗練されることになります。
さて、充分に試行回数を稼いだらプレイヤーが実際にする行動を決めるのですが、勝率でもなく、UCB1でもなく、試行回数が多い行動を選択します。
一見すると勝率が多い行動を選択するとよさそうですが、MCTSの場合は探索途中で勝率が高いノードが多く選ばれているはずなので、試行回数の多さは探索途中の勝率の高さの裏付けともいえます。そのため、探索を終えた段階で、仮にたまたま最終勝率が他のノードより低かったとしても、試行回数が多いノードはより信頼ができそうです。
// 配列の最大値のインデックスを返す
int argMax(const std::vector<double>& x) {
return std::distance(x.begin(), std::max_element(x.begin(), x.end()));
}
double playout(State* state);// 先述と同じ
constexpr const double C = 1.; //UCB1の計算に使う定数
constexpr const int EXPAND_THRESHOLD = 10; // ノードを展開する閾値
// MCTSの計算に使うノード
class Node {
private:
State state_;
double w_;
public:
std::vector<Node>child_nodes;
double n_;
// ノードの評価を行う
double evaluate() {
if (this->state_.isDone()) {
double value = this->state_.isLose() ? 0 : 0.5;
this->w_ += value;
++this->n_;
return value;
}
if (this->child_nodes.empty()) {
State state_copy = this->state_;
double value = playout(&state_copy);
this->w_ += value;
++this->n_;
if (this->n_ == EXPAND_THRESHOLD)
this->expand();
return value;
}
else {
double value = 1. - this->nextChiledNode().evaluate();
this->w_ += value;
++this->n_;
return value;
}
}
// ノードを展開する
void expand() {
auto legal_actions = this->state_.legalActions();
this->child_nodes.clear();
for (const auto action : legal_actions) {
this->child_nodes.emplace_back(this->state_);
this->child_nodes.back().state_.advance(action);
}
}
// どのノードを評価するか選択する
Node& nextChiledNode() {
for (auto& child_node : this->child_nodes) {
if (child_node.n_ == 0)
return child_node;
}
double t = 0;
for (const auto& child_node : this->child_nodes) {
t += child_node.n_;
}
double best_value = -INF;
int best_i = -1;
for (int i = 0; i < this->child_nodes.size(); i++) {
const auto& child_node = this->child_nodes[i];
double wr = 1. - child_node.w_ / child_node.n_;
double bias = std::sqrt(2. * std::log(t) / child_node.n_);
double ucb1_value = 1. - child_node.w_ / child_node.n_ + (double)C * std::sqrt(2. * std::log(t) / child_node.n_);
if (ucb1_value > best_value) {
best_i = i;
best_value = ucb1_value;
}
}
return this->child_nodes[best_i];
}
Node(const State& state) :state_(state), w_(0), n_(0) {}
};
// プレイアウト数を指定してMCTSで行動を決定する
Action mctsAction(const State& state, const int playout_number) {
Node root_node = Node(state);
root_node.expand();
for (int i = 0; i < playout_number; i++) {
root_node.evaluate();
}
auto legal_actions = state.legalActions();
int best_n = -1;
int best_i = -1;
assert(legal_actions.size() == root_node.child_nodes.size());
for (int i = 0; i < legal_actions.size(); i++) {
int n = root_node.child_nodes[i].n_;
if (n > best_n) {
best_i = i;
best_n = n;
}
}
return legal_actions[best_i];
}
Githubには指定した時間いっぱいまで深く探索するコードも載せています。
同時着手二人ゲームに使いたい探索アルゴリズム
ゲーム例:同時数字集め迷路
○×ゲームは同時着手に向かないため、一人ゲームの章で説明した数字集め迷路を同時着手二人ゲームに拡張した説明用オリジナルゲームで説明していきます。
ゲームの目的:迷路を進みながら3ターン後の時点のスコアを高くする。
プレイヤー二人それぞれに用意されたキャラクター(A, B)は、1ターンに上下左右四方向のいずれかに壁(#)のない場所に1マスずつ進む。
床にあるポイント(1~9)を踏むと自身のスコアとなり、床のポイントが消える。(.)
プレイヤーの行動は同時で、同じ位置に重なった場合は両者がスコアを獲得する。
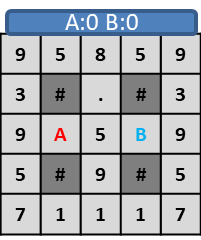
このような盤面でプレイヤーAが右、プレイヤーBが左に移動した場合、
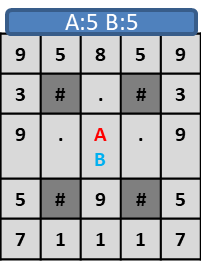
プレイヤーA,プレイヤーBが同じ位置に重なり、両者がスコア5となります。
ここで、交互着手ゲームで説明したAlphaBetaやMCTSではプレイヤーが交互に行動することを前提としたシミュレーションをするため、上記の流れをシミュレーションすると、以下のようになります。
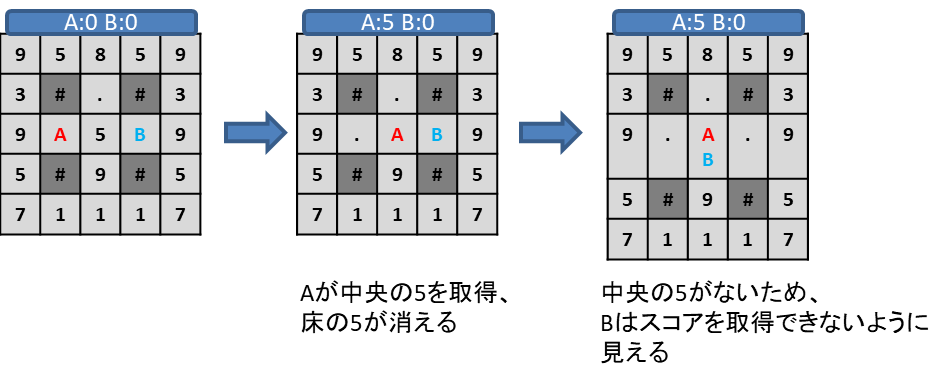
このゲームの場合、本来プレイヤーAとプレイヤーBの両社がスコア5になっているはずなので、このような間違ったシミュレーションをすると、特定の行動を不当に高く評価したり低く評価したりしてしまいます。
そのため、同時着手ゲームには同時着手の特性を加味した探索アルゴリズムが必要となります。
同時着手二人ゲームのクラス設計
例のごとく、同時数字集め迷路の実装例はgithubに載せています。
class State {
public:
// プレイヤー0が勝ったか判定する
bool isWin()const;
// プレイヤー0が負けたか判定する
bool isLose()const;
// 引き分けになったか判定する
bool isDraw()const;
// ゲームが終了したか判定する
bool isDone()const;
// 指定したactionでゲームを1ターン進める
void advance(const Action action0, const Action action1);
// 指定したプレイヤーが可能な行動を全て取得する
Actions legalActions(const int player_id)const;
};
DUCT(Decoupled Upper Confidence Tree)
先述の通り、MCTSはそのまま同時着手ゲームに利用することができません。
そこで、自分と相手の行動を同時に選択することにします。
まず、自分ができる行動の数がN, 相手ができる行動の数がMとすると、次のターンに起きうる盤面のパターンはN×Mです。
ここでN×Mの二次元配列で子ノードを管理します。
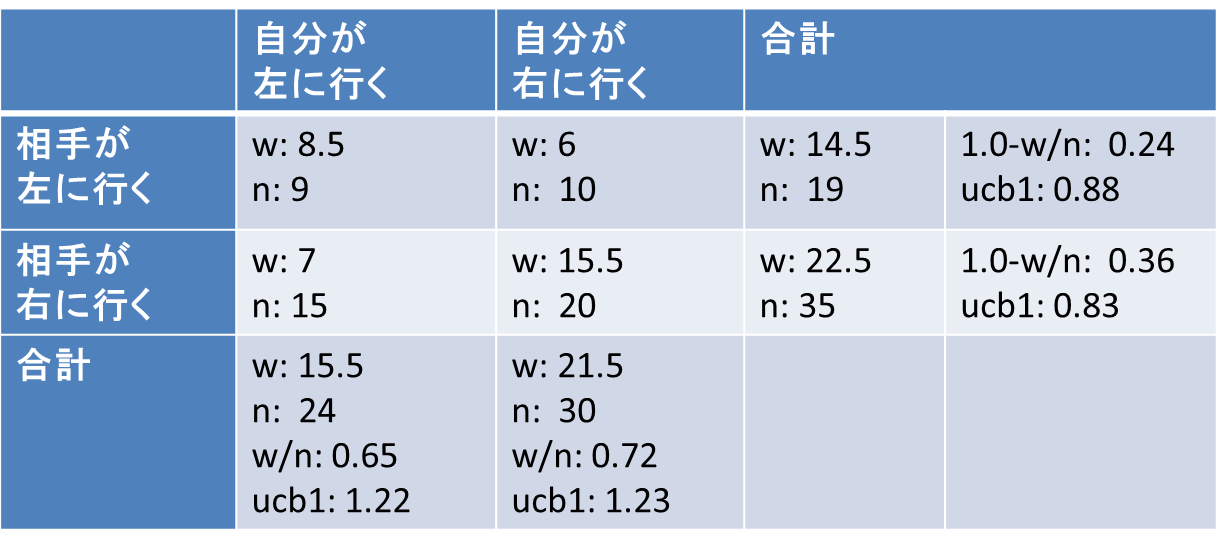
MCTSと同じように各ノードの累計価値と試行回数を覚えておきます。
ここで、行動を自分と相手でそれぞれ独立に選択します。
上の表の場合、自分が左に行く行動の累計価値と試行回数は、「自分が左に行き、相手が左に行く」ノードの「w: 8.5, n: 9」と「自分が左に行き、相手が右に行く」ノードの「w: 7, n: 15」の合計で「w: 15.5, n: 24」となります。あとはこの値を利用してそのままucb1を計算すれば1.22となります。
同様に自分が右に行く行動のucb1を計算し、ucb1が最大の行動を選択します。
相手に対しても同様にucb1を計算して相手の行動を選択します。
注意点として、各ノードの累計価値を自分視点で記録している場合、相手の行動のucb1計算に使う勝率は相手視点になるように計算し直す必要があります。
ゲームが零和(どちらかのプレイヤーが得した場合、もう片方のプレイヤーがその得と同量の損をする)なら片方のプレイヤーの累計価値を覚えておけば他方のプレイヤーの累計価値も計算(上の表では1.0-w/n)で求められますが、零和ではない場合、プレイヤーごとに累計価値をメモしたほうがよさそうです。サンプルコードでは零和前提で実装しています。
展開はMCTSと同じで、各ノードを訪れた回数が指定回数に達した時に展開するだけです。
他はだいたい普通のMCTSと同じです。
なお、同時着手ゲームなら常にDUCTを使えばよいかというとそうでもないらしく、普通のMCTSと比較して、DUCTがやや不利になるゲームがあるという報告もあるようです。
MCTSと比較して、子ノードの多いDUCTは収束性が悪く、深い読みが弱いようです。
ゲームの合法手の多さや探索対象となる空間の大きさ、同時着手性によるゲーム影響度など、ゲームの性質と相談しながらMCTSとDUCTのどちらを使うか考えるとよさそうです。
// 配列の最大値のインデックスを返す
int argMax(const std::vector<double>& x) {
return std::distance(x.begin(), std::max_element(x.begin(), x.end()));
}
//プレイヤー0視点での評価
double playout(State* state) { // const&にすると再帰中にディープコピーが必要になるため、高速化のためポインタにする。(constでない参照でも可)
if (state->isWin())
return 1;
if (state->isLose())
return 0;
if (state->isDraw())
return 0.5;
state->advance(randomAction(*state, 0), randomAction(*state, 1));
return playout(state);
}
constexpr const double C = 1.; //UCB1の計算に使う定数
constexpr const int EXPAND_THRESHOLD = 5; // ノードを展開する閾値
// DUCTの計算に使うノード
class Node {
private:
State state_;
double w_;
public:
std::vector<std::vector<Node>>child_nodeses;
double n_;
// ノードの評価を行う
double evaluate() {
if (this->state_.isDone()) {
double value = 0.5;
if (this->state_.isWin())value = 1.;
else if (this->state_.isLose())value = 0.;
this->w_ += value;
++this->n_;
return value;
}
if (this->child_nodeses.empty()) {
State state_copy = this->state_;
double value = playout(&state_copy);
this->w_ += value;
++this->n_;
if (this->n_ == EXPAND_THRESHOLD)
this->expand();
return value;
}
else {
double value = this->nextChiledNode().evaluate();
this->w_ += value;
++this->n_;
return value;
}
}
// ノードを展開する
void expand() {
auto legal_actions0 = this->state_.legalActions(0);
auto legal_actions1 = this->state_.legalActions(1);
this->child_nodeses.clear();
for (const auto& action0 : legal_actions0) {
this->child_nodeses.emplace_back();
auto& target_nodes = this->child_nodeses.back();
for (const auto& action1 : legal_actions1) {
target_nodes.emplace_back(this->state_);
auto& target_node = target_nodes.back();
target_node.state_.advance(action0, action1);
}
}
}
// どのノードを評価するか選択する
Node& nextChiledNode() {
for (auto& child_nodes : this->child_nodeses) {
for (auto& child_node : child_nodes) {
if (child_node.n_ == 0)
return child_node;
}
}
double t = 0;
for (auto& child_nodes : this->child_nodeses) {
for (auto& child_node : child_nodes) {
t += child_node.n_;
}
}
int best_is[] = { -1,-1 };
double best_value = -INF;
for (int i = 0; i < this->child_nodeses.size(); i++) {
const auto& childe_nodes = this->child_nodeses[i];
double w = 0;
double n = 0;
for (int j = 0; j < childe_nodes.size(); j++) {
const auto& child_node = childe_nodes[j];
w += child_node.w_;
n += child_node.n_;
}
double wr = w / n;
double bias = std::sqrt(2. * std::log(t) / n);
double ucb1_value = w / n + (double)C * std::sqrt(2. * std::log(t) / n);
if (ucb1_value > best_value) {
best_is[0] = i;
best_value = ucb1_value;
}
}
best_value = -INF;
for (int j = 0; j < this->child_nodeses[0].size(); j++) {
double w = 0;
double n = 0;
for (int i = 0; i < this->child_nodeses.size(); i++) {
const auto& child_node = child_nodeses[i][j];
w += child_node.w_;
n += child_node.n_;
}
w = 1. - w;
double wr = w / n;
double bias = std::sqrt(2. * std::log(t) / n);
double ucb1_value = w / n + (double)C * std::sqrt(2. * std::log(t) / n);
if (ucb1_value > best_value) {
best_is[1] = j;
best_value = ucb1_value;
}
}
return this->child_nodeses[best_is[0]][best_is[1]];
}
Node(const State& state) :state_(state), w_(0), n_(0) {}
};
// プレイアウト数を指定してDUCTで指定したプレイヤーの行動を決定する
Action ductAction(const State& state, const int player_id, const int playout_number) {
Node root_node = Node(state);
root_node.expand();
for (int i = 0; i < playout_number; i++) {
root_node.evaluate();
}
auto legal_actions = state.legalActions(player_id);
int i_size = root_node.child_nodeses.size();
int j_size = root_node.child_nodeses[0].size();
if (player_id == 0) {
int best_n = -1;
int best_i = -1;
for (int i = 0; i < i_size; i++) {
int n = 0;
for (int j = 0; j < j_size; j++) {
n += root_node.child_nodeses[i][j].n_;
}
//std::cout << dstr[legal_actions[i]] << " " << n << std::endl;
if (n > best_n) {
best_i = i;
best_n = n;
}
}
//std::cout <<"best\t" << dstr[legal_actions[best_i]] << " " << best_n << std::endl;
return legal_actions[best_i];
}
else {
int best_n = -1;
int best_j = -1;
for (int j = 0; j < j_size; j++) {
int n = 0;
for (int i = 0; i < i_size; i++) {
n += root_node.child_nodeses[i][j].n_;
}
if (n > best_n) {
best_j = j;
best_n = n;
}
}
return legal_actions[best_j];
}
}
Githubには指定した時間いっぱいまで深く探索するコードも載せています。
想定質問集
-
Q. 一人ゲームってビームサーチ系の手法以外にもやきなまし系の手法や遺伝的アルゴリズムも使えるのでは?
A. 実はこれらの手法を紹介するか迷っていました。マラソンマッチでは定番の手法ですし、ゲームでも使える場面はあると思います。ビームサーチはこれらの手法と比べて、文脈のある問題に強いという特性があります。今回紹介したように、ターンの概念があり、1ターンずつプレイヤーの行動で盤面が動くというゲームの場合、行動の順序によって盤面が大きく変わってしまいます。ビームサーチは浅い探索で行動が決定された状態で深いノードから探索を進めるため、これらの文脈を維持したままの探索が可能になる点、文脈のあるゲームでは優れています。探索を深さ1から繰り返すChokudaiサーチも、一つ一つのノードを見れば過去の探索結果からの文脈を引き継ぐため、同様の恩恵を得られます。その点、焼きなましや遺伝的アルゴリズムで探索をするなら、設定した深さまでの行動をランダムに動かすことになるため、文脈を維持した探索は難しいです。探索空間があまりにも大きくてビームサーチ系のアルゴリズムでは探索が難しい場合は他のアルゴリズムを試す可能性もありますが、その場合初心者が試すべき手法はGreedyだと判断しました。 -
Q. 一人ゲームの例にぷよぷよがあるけど、二人以上のゲームでは?
A. ぷよぷよ(通など)はたしかに二人以上のゲームで、連鎖の打ち合いによって相手の行動によって自分の盤面の状況が変化しうるゲームです。その一方で、ゲーム全体を見た時に相手の行動を意識する必要がある時間よりも圧倒的に自分の盤面内で連鎖を組む方法を考える時間が多いゲームです。その点、探索をする際に相手の行動を無視した方がより深い探索ができます。大連鎖を組むにしろ、中規模の連鎖を高速に打ち込んで速攻を仕掛けるにしろ、探索効率は大きな武器となるため、探索アルゴリズムの観点では一人ゲームとして扱うとよいです。もちろん、完全に一人だけのゲームでもありませんから、ここで紹介した以外のアルゴリズムを使う方法を考えてみるのもおもしろいかもしれません。 -
Q. 他のサイトで見たChokudaiサーチの実装では、親ノードへの参照を持ってさかのぼるような実装になっていました。なぜそれをしていないのですか?
A. 各ターンごとにとる行動1つのみを選択すればよいゲームを想定しています。たとえば、探索し終わった後にどの道筋でその盤面に至ったのかを深さ0から全て知りたいような状況では親ノードへの参照を持っていたほうがよいのでしょう。何を目的にどんな用途でChokudaiサーチを使うのかを考慮した上で実装方針を決めるとよいでしょう。 -
Q. MCTSって機械学習の手法じゃないんですか?よく機械学習の文献とかで見かけます。
A. もしかしてアルファ碁やアルファゼロについての文献を読んでいる人でしょうか。あれは「機械学習と探索を組み合わせた」手法で、MCTSは探索です。アルファ碁がMCTSを使っていただけで、機械学習と組み合わせないといけない手法ではないです。むしろアルファ碁の使い方はランダム要素がなく、モンテカルロを名乗っているのが謎です。 -
Q. 出版社の者です。この記事に感銘を受けました!ぜひ書籍化のご検討をお願いしたいです!
A.ありがとうございます!とても光栄です!twitterにて@thun_c宛てにDMをお待ちしています!
https://twitter.com/thun_c
本記事を元に
ゲームで学ぶ探索アルゴリズム実践入門~木探索とメタヒューリスティクス
という書籍を出版することになりました!ありがとうございます!
まとめ
ゲームの種類ごとに、AIに利用できる探索アルゴリズムの概要と実装方法について説明しました。
今回は具体的なゲームを例示しながら説明しましたが、基本的にはゲームの大別が同じであればそのままサンプルコードを適用可能です。
ぜひご自身のお好きなゲームでAIを実装して楽しんでいただければと思います。
参考文献