二項分布を正規分布の形で近似する

はじめに

二項分布と正規分布が一致する条件を調べる。

二項分布

P(X=k)={ }_{n} \mathrm{C}_{k} p^{k}(1-p)^{n-k} \quad(k=0,1,2, \cdots, n)

についてp=1/2、n=100とすると

P(X=k)= \frac{{ }_{100} \mathrm{C}_{k}}{2^{100}} \quad(k=0,1,2, \cdots, n)

正規分布

p(x)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}

についてμ=50、σ=5とすると

p(x)=\frac{1}{5\sqrt{2 \pi }} e^{-\frac{(x-50)^{2}}{50}}

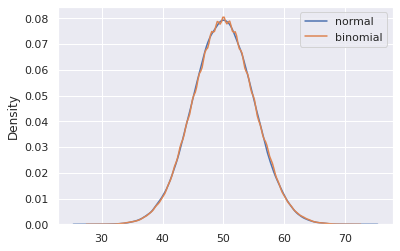
プロットしてみる

from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

sns.set()
sns.kdeplot(random.normal(loc=50, scale=5, size=100000), label='normal')
sns.kdeplot(random.binomial(n=100, p=0.5, size=100000), label='binomial')

plt.legend()
plt.show()

二項分布を正規分布の形に近似する

スターリングの公式を使うと次の近似が成り立つ。

\frac{n !}{k !(n-k) !} p^{k}(1-p)^{n-k} \approx \frac{1}{\sqrt{2 \pi n p(1-p)}} \exp \left\{-\frac{(k-n p)^{2}}{2 n p(1-p)}\right\}