Go to Qiita Advent Calendar 2024 Top
LoginSignup
16
19

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@tharashi

K-Shape法を用いて心電図データをクラスタリングしてみた

Posted at

本記事サマリ

  • K-Shape法を用いて時系列データをクラスタリングしてみる

データセット

  • 今回はカリフォルニア大学リバーサイド校の時系列データコレクション(UCR Time Series Classification Archive)を使います

  • 心電図(ECG)は心疾患検出を促進するものとして知られています

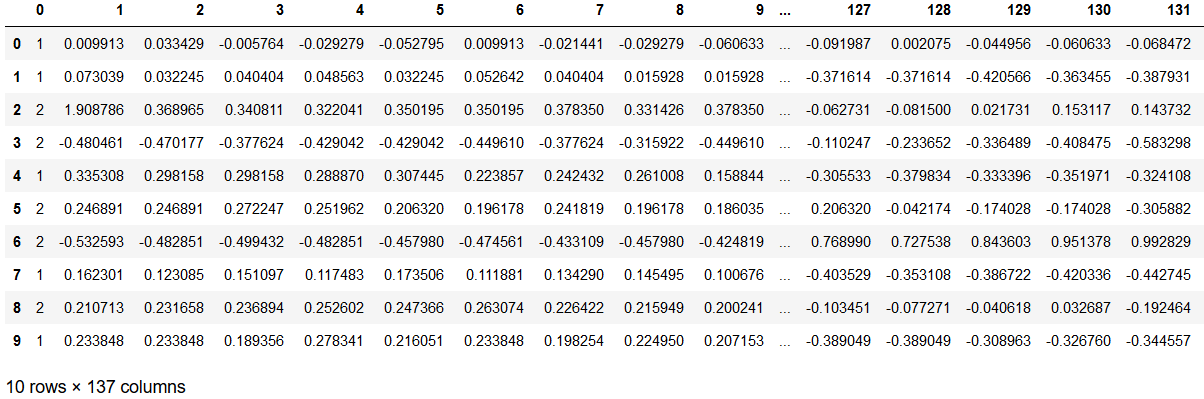
  • 使用するECGFiveDays_TRAIN.tsvの中身は以下の通りです

DataFrame
df = pd.read_table("ECGFiveDays_TRAIN.tsv",header=None)
df.head(10)

image.png

データサマリはこちら

Summary
import numpy as np
import matplotlib.pyplot as plt
from tslearn.utils import to_time_series_dataset

data_train = np.loadtxt("ECGFiveDays_TRAIN.tsv")
X_train = to_time_series_dataset(data_train[:,1:])
print("時系列データの総数 : ",len(data_train))
print("クラスの数 : ", len(np.unique(data_train[:,0])))
print("時系列の長さ : ",len(data_train[0,1:]))

----------------------
#時系列データの総数 :  23
#クラスの数 :  2
#時系列の長さ :  136

136スナップある時系列データが計23本含まれております。欠損値はありません。

Vizualize
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
for i in range(0,3):
    if data_train[i,0]==2.0:
        plt.figure(figsize=(18, 8))
        print("Plot",i,"Class",data_train[i,0])
        plt.plot(data_train[i],c='r')
        plt.show()

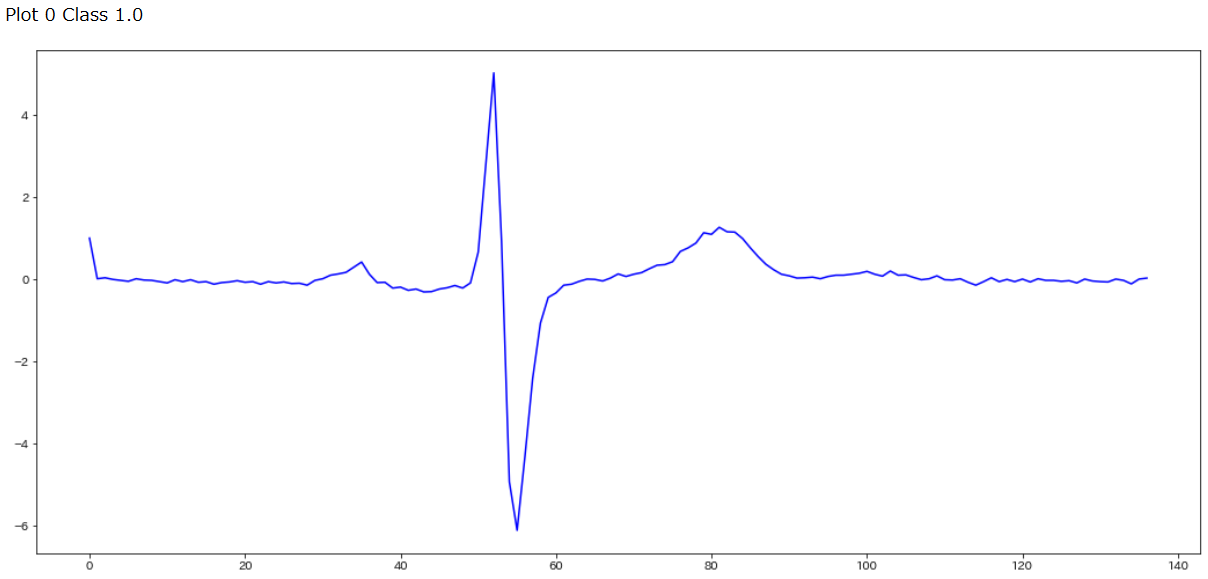
image.png

image.png

これらのラベルは心電図の専門家がつけたラベルなので、クラス1.0もクラス2.0も素人の目だとほとんど区別がつきません。また補足で、ECGFiveDays_TRAIN.tsvと一緒にダウンロードされるReadme.mdによるとこの心電図は1990年に測定された67歳の男性のECGデータであるそうです。

前処理

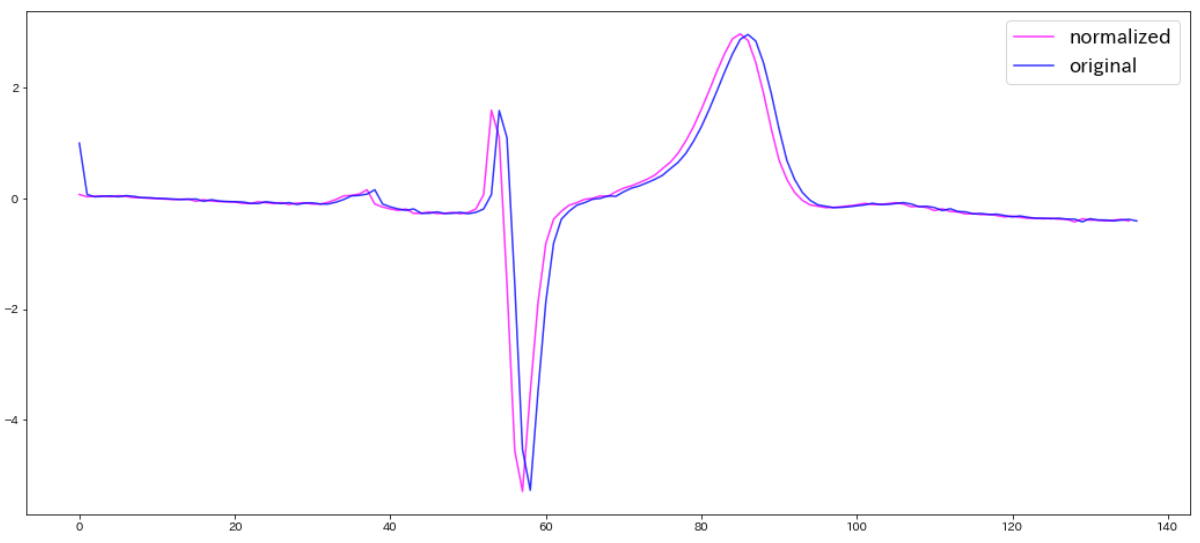
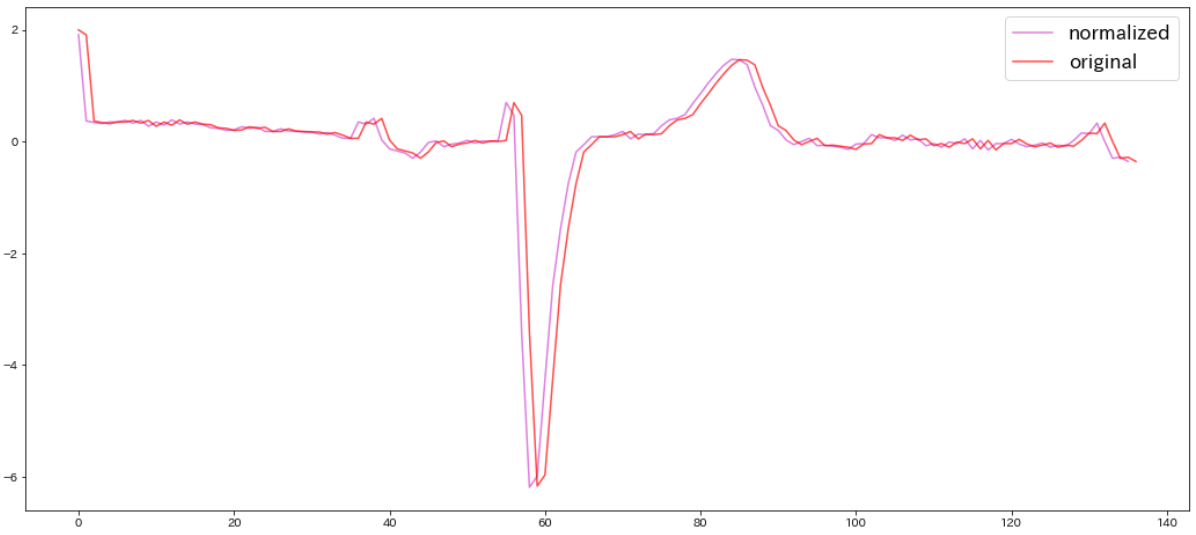
K-Shapeに持ち込むために、各時系列データを平均0、標準偏差1になるように正規化します。ここでは先ほどのPlot0,class1.0の心電図を正規化し、グラフ化して比較してみます。

正規化
from tslearn.preprocessing import TimeSeriesScalerMeanVariance
from tslearn.utils import to_time_series_dataset
X_train = to_time_series_dataset(data_train[:,1:])
X_train = TimeSeriesScalerMeanVariance(mu=0.,std=1.).fit_transform(X_train)
plt.figure(figsize=(18, 8))
plt.plot(X_train[1],c='magenta',alpha=0.8,label="normalized")
plt.plot(data_train[1],c='blue',alpha=0.8,label="original")
plt.legend(fontsize=17)

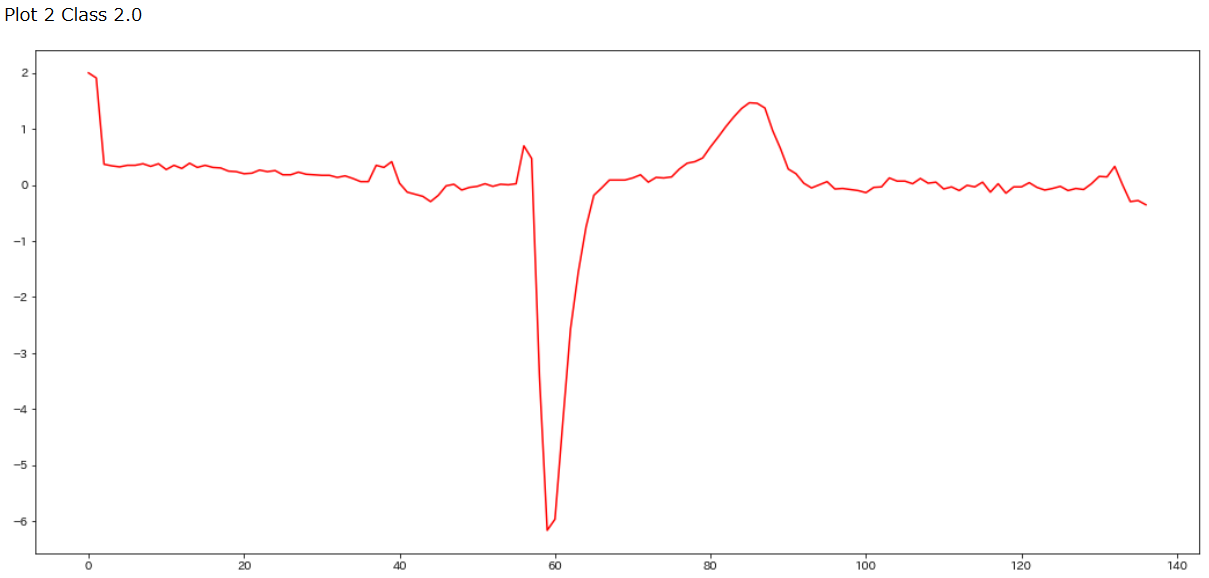
image.png

※先ほどのクラス2.0の赤いグラフも正規化したものと比較すると下図のようになります。
image.png

K-Shape法について

端的に3点でまとめてみます。

  • 時系列データを対象とした形状ベースのクラスタリング手法です
  • 基本的にはk-meansと同じですが、距離の測り方が違います
  • 下記がK-Shapeの論文です。2015年に書かれたものなのでアルゴリズム自体は比較的新しいです(
    https://dl.acm.org/doi/10.1145/2723372.2737793)

いざ、訓練

クラスタ数を2、最大繰り返し回数100、訓練回数を100として実行します。

Train
from tslearn.clustering import KShape
ks = KShape(n_clusters=2,max_iter=100,n_init=100,verbose=0)
ks.fit(X_train)
y_pred = ks.fit_predict(X_train)
print(y_pred)

---
#[0 1 0 0 1 0 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 0 1]

計23本の時系列に対して、2種類のクラスどちらに分類されるか予測ラベルを付けることが出来ました。K-Shapeに関するハイパーパラメータは下記URLを参照しております。
https://tslearn.readthedocs.io/en/stable/gen_modules/clustering/tslearn.clustering.KShape.html

評価

時系列クラスタリングの評価尺度として、調整ランド指標を用います。一言で言うと、この指標は「予測されたクラスタリングと真のクラスタリングの間でどれだけクラスタ割り当てが一致しているか」を測るものです。

ここではScikit-learnのadjusted_rand_scoreを用います。
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.adjusted_rand_score.html

評価(訓練データに対して)
from sklearn.metrics import adjusted_rand_score
ars = adjusted_rand_score(data_train[:,0],y_pred)
print("調整ランド指標 : ",ars)
---
#調整ランド指標 :  0.668041237113402

次はテストデータに対するarsを求めます。

評価(テストデータに対して)
import numpy as np
import matplotlib.pyplot as plt
from tslearn.utils import to_time_series_dataset

data_test = np.loadtxt("ECGFiveDays_TEST.tsv")
X_test = to_time_series_dataset(data_test[:,1:])
pred_test = ks.predict(X_test)
ars = adjusted_rand_score(data_test[:,0],pred_test)
print("調整ランド指標 : ",ars)
---
#調整ランド指標 :  0.06420517898316379

とても低いスコアが出てしまいました。

0に近いスコア=ランダム割り当てした時のスコア

というロジックなので、良いモデルであるとは決して言えません。テストデータに対するスコアが低い理由としては「圧倒的にデータ数が少ない」からと考えられます。そこでデータ数を増やして同じトライしてみます。

ECG5000データを使って訓練/評価

以下では、UCR Archiveに梱包されているECG5000_TRAIN.tsvとECG500_TEST.tsvを使用します。

ECG5000のデータセット
import numpy as np
import matplotlib.pyplot as plt
from tslearn.utils import to_time_series_dataset
from sklearn.model_selection import train_test_split

data_test_ = np.loadtxt("ECG5000_TEST.tsv")
data_train_ = np.loadtxt("ECG5000_TRAIN.tsv")
data_joined = np.concatenate((data_train_,data_test_),axis=0)
data_train_,data_test_ =train_test_split(data_joined,test_size=0.2,random_state=2000) 

X_train_ = to_time_series_dataset(data_train_[:,1:])
X_test_ = to_time_series_dataset(data_test_[:,1:])

print("時系列データの総数 : ",len(data_train_))
print("クラスの数 : ", len(np.unique(data_train_[:,0])))
print("時系列の長さ : ",len(data_train_[0,1:]))

---
#時系列データの総数 :  4000
#クラスの数 :  5
#時系列の長さ :  140

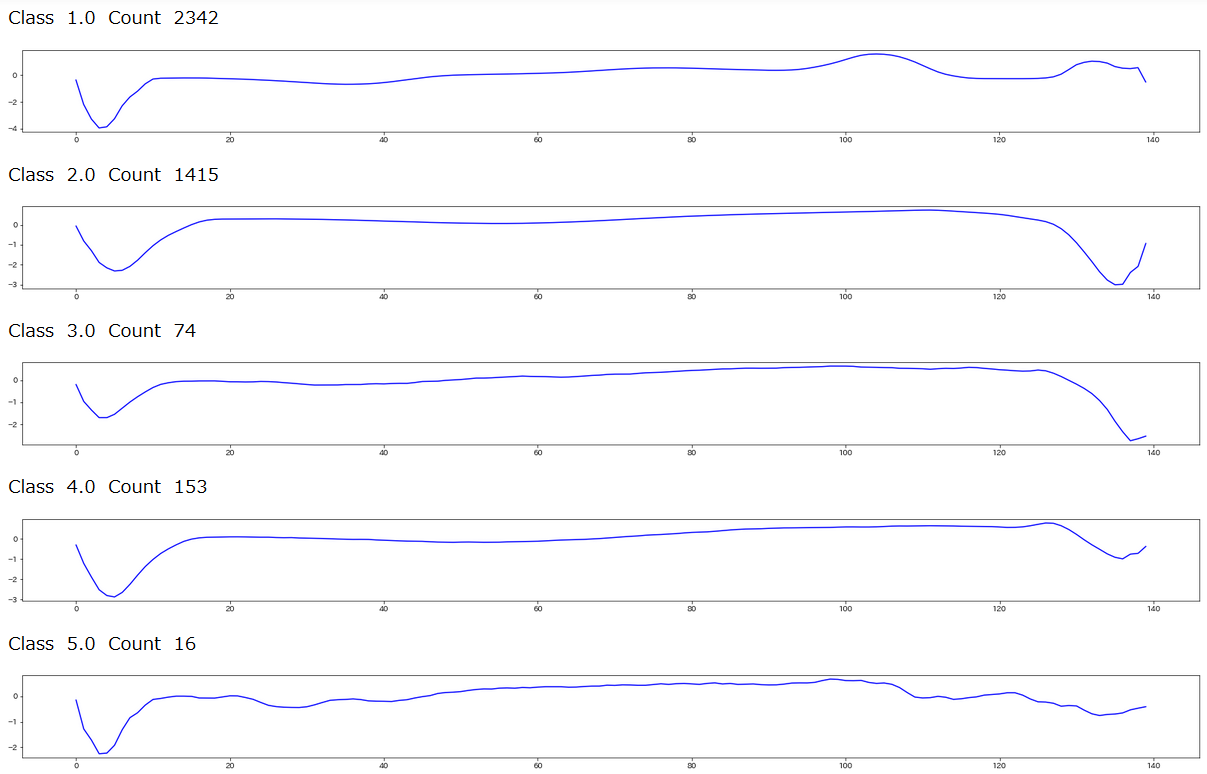
クラスタに属しているデータ数はこちら

クラスタ詳細
print("クラス1.0に属するデータ数",len(data_train_[data_train_[:,0]==1.0]))
print("クラス1.0に属するデータ数",len(data_train_[data_train_[:,0]==2.0]))
print("クラス1.0に属するデータ数",len(data_train_[data_train_[:,0]==3.0]))
print("クラス1.0に属するデータ数",len(data_train_[data_train_[:,0]==4.0]))
print("クラス1.0に属するデータ数",len(data_train_[data_train_[:,0]==5.0]))
---
#クラス1.0に属するデータ数 2342
#クラス1.0に属するデータ数 1415
#クラス1.0に属するデータ数 74
#クラス1.0に属するデータ数 153
#クラス1.0に属するデータ数 16

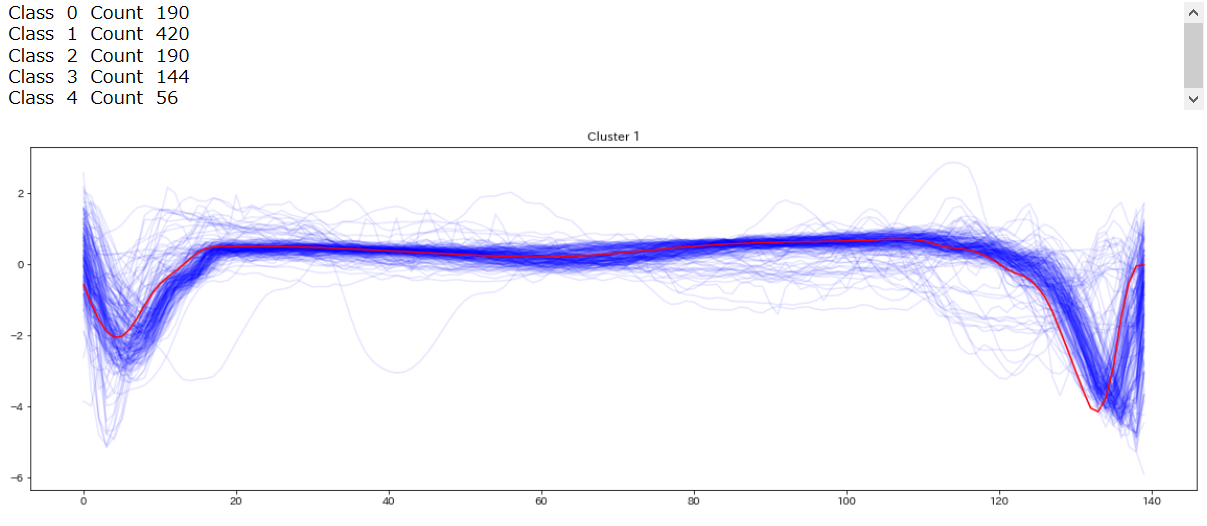
グラフにするとこんな感じです

各クラスタの可視化
%matplotlib inline
import matplotlib.pyplot as plt

for j in np.unique(data_train_[:,0]):
    plt.figure(figsize=(28,2))
    dataPlot = data_train_[data_train_[:,0]==j]
    cnt = len(dataPlot) 
    dataPlot = dataPlot[:,1:].mean(axis=0)
    print(" Class ",j," Count ",cnt)
    plt.plot(dataPlot,c='b')
    plt.show()

image.png

先ほどと同様に訓練&評価していきます

訓練/評価(テストデータに対して)
from tslearn.preprocessing import TimeSeriesScalerMeanVariance
from tslearn.utils import to_time_series_dataset
from tslearn.clustering import KShape
from sklearn.metrics import adjusted_rand_score
X_train_ = to_time_series_dataset(data_train_[:,1:])
X_train_ = TimeSeriesScalerMeanVariance(mu=0.,std=1.).fit_transform(X_train_)
X_test_ = to_time_series_dataset(data_test_[:,1:])
X_test_ = TimeSeriesScalerMeanVariance(mu=0.,std=1.).fit_transform(X_test_)

ks = KShape(n_clusters=5,max_iter=100,n_init=100,verbose=1,random_state=2000)
ks.fit(X_train_)
preds_test = ks.predict(X_test_)
ars_ = adjusted_rand_score(data_test_[:,0],preds_test)
print("調整ランド指標 : ",ars_)
---
#調整ランド指標 :  0.4984050982000773

テストデータに適用したときの評価ランド指標は、約0.498となりました。先ほどのデータ適用と比べると雲泥の差です。訓練セットのサイズを23本から4000本にしたことではるかに精度の良いモデルが作成されました。

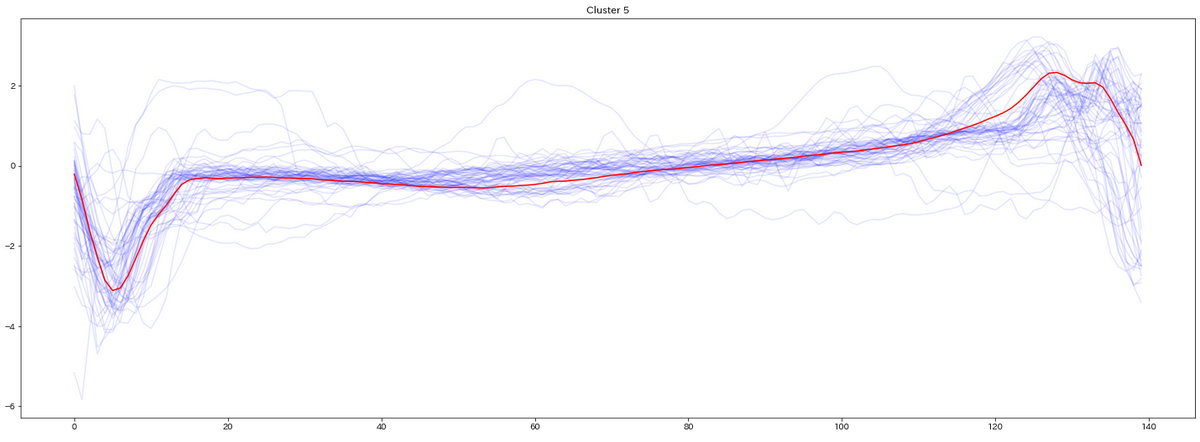
最後にテストデータを見てみます

分類結果の可視化
for yi in range(5):
    plt.figure(figsize=(20,35))
    plt.subplot(5, 1, 1 + yi)
    for xx in X_test_[preds_test == yi]:
        plt.plot(xx.ravel(), alpha=0.1,c='blue')
    cnt = len(X_test_[preds_test == yi]) 
    
    plt.plot(ks.cluster_centers_[yi].ravel(), "red")
    print(" Class ",yi," Count ",cnt)
    plt.title("Cluster %d" % (yi + 1) )

plt.tight_layout()
plt.show()

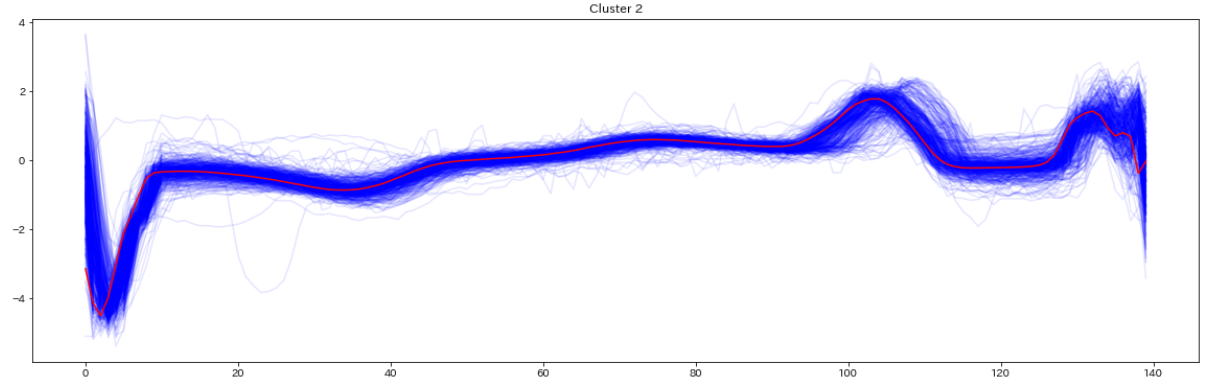
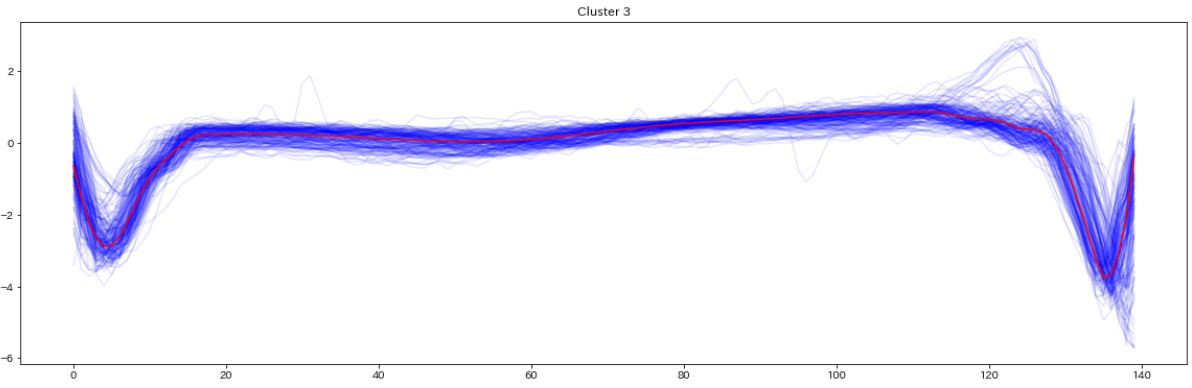
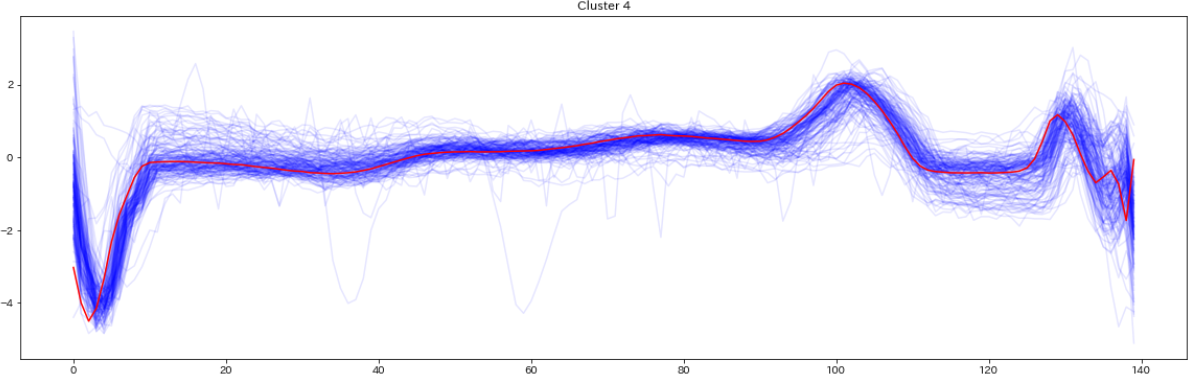
テストデータの分類結果を可視化したものがこちら(赤い線はセントロイド)
image.png

image.png

image.png

image.png

image.png

#まとめ

  • 今回は形状ベースのK-Shapeと心電図データを使って時系列クラスタリングを試みました
  • データ数を増やすことで、調整ランド指標のスコアが爆上がりしました
  • K-Shape以外にもk-meansやDBSCANでもクラスタリングできるので今後比較も行いたい

#補足

K-Shapeの距離測定

SBD(\vec{x},\vec{y})=1-\underset{w}{max}\frac{CC_w(\vec{x},\vec{y})}{\sqrt{R_0(\vec{x},\vec{x})}\sqrt{R_0(\vec{y},\vec{y})}}
  • 時系列データに上手く適合する類似度、相互相関$CC_w$を導入しています
  • $SBD$は $\vec{x},\vec{y}$ の距離を意味しています

###tslearnとは
tslearnは機械学習を使った時系列分析用のPythonパッケージです。 K-Shape以外にも様々な時系列分析アルゴリズムが含まれています

参考文献

16
19
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
16
19

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?