1.はじめに
わたくし事ですが最近引越しまして、
クリスマス直前だっていうのに殺風景な部屋に独りぼっちなわけです。
「よし、クリスマスツリーでも作って飾ろう」
しかし、ただ市販のツリーを買ってきて、装飾して…なんてやっていたら余計に淋しさで押しつぶされそうなので、
「セル・オートマトンでクリスマスツリーのイルミネーション作ったら面白いんじゃないか!?」
と、思い立ったわけです。
そんなわけで、折角なのでライフゲームのルールでクリスマスツリー(のような何か)を光らせてみました。
結果は下の方にあるので、内容に興味がなければすっ飛ばしてください。
2.セル・オートマトンとは
離散的計算モデルのひとつです。
格子状のマス目(セル)に、それぞれ「生きている」「死んでいる」のいずれかの状態を持たせます。
現在のセルの状態を元に、次のセルの状態を計算し、それを繰り返して格子状に並んだセル全体の様子を観察します。
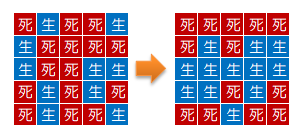
シミュレーションの例
様々なシミュレーションに応用されていますのでいくつか紹介します。
数理シミュレーションは複雑な微分方程式や積分方程式などを構築するイメージがありますが、
セル・オートマトンは非常に単純なルールで、複雑且つ面白い振る舞いを観測できるので、割ととっつきやすいと思います。
セル・オートマトンとカオス
セル・オートマトンでは、カオティックな振る舞いも観測できます。
上述したように、シミュレーションの構成自体は非常にシンプルであるにもかかわらず、カオス的な振る舞いを再現できることも、セル・オートマトンが注目された要因のひとつです。
ちなみに、カオスの応用例として、クリスマスイルミネーションの光らせ方とか、蝋燭の灯のリアルな揺らぎとかが既に研究されています。
株価予測に応用して大儲けした人たちも居たとかいないとか。
3.ライフゲームとは
イギリスの数学者Conwayが考案した,生命の誕生と死のシミュレーションです。
ルール
セル・オートマトンは「現在のセルの状態を元に、次のセルの状態を計算」と書きましたが、
ライフゲームにおける、その「計算」のルールは非常にシンプルです。
- [誕生]:死んでいるセルに隣接する生きたセルがちょうど3つあれば、次の世代が誕生する。
- [生存]:生きているセルに隣接する生きたセルが2つか3つならば、次の世代でも生存する。
- [過疎]:生きているセルに隣接する生きたセルが1つ以下ならば、過疎により死滅する。
- [過密]:生きているセルに隣接する生きたセルが4つ以上ならば、過密により死滅する。
たったこれだけです。
生物の淘汰や、進化などのプロセスをとても単純なルールでモデル化したものなのですが、
なかなかどうして、面白い振舞いをするのです。
ライフゲームについてはこちらの記事を参考にさせていただきました。
「Javaでライフゲームを作る」
4.こうなった

シミュレーション範囲:木の葉っぱの部分
生存:黄色
死亡:緑色
初期状態:各セルに一様乱数を振り、30%の確率で生存
繰返回数:5000回(収束したので画像は途中で切っています)
試行回数:面白い動きが出るまで
プログラムはJavaで書きました。描画処理はSwingを使っています。
↓ソースはこちら(美しくないので悪しからず…。)
https://github.com/tf-tky/XmasLifeGame
思ったこと
- てっぺんは初期状態以外光らないよなあ(光りません)
- 木の上の方に行くにしたがってセルの数が減るので、すぐに消えてしまうのでは(そうでもなかった)
- イルミネーションぽく見せるためにランダム性を持つルールを追加したほうが良いかなあ(やってみたけどイマイチだった)