最近、何かとLSTMという単語を聞くので少し勉強して、使ってみたいと思いやってみた。似たような記事は多いが、私の記憶定着を兼ねたものとなっているので、ゴミ記事扱いしないでください。
この記事を書いているとき、ひたすらマサカリが飛んでいる記事がトレンドに乗っていたので、一言書いておきます。
記事中に、LSTMの理論を理解したと書いてありますが完全に理解したわけではなく、大まかに何が行われているかを理解しただけです。決して数式を完璧に理解したわけではありません。
##そもそもLSTMとは
単語はよく聞くがどういうものなのだろう。LSTMは、RNNの一種だが大きく違う点は長期記憶に優れている点である。通常のRNNでは、勾配消失が起きてしまい、短期的なデータにしか使うことができなかった。しかし、勾配消失を解決したのがLSTMである。LSTMのほかにGRUもあるが、今回は触れないことにする。
##勾配消失をどうやって解決したのか（LSTM）
記憶セル、入力ゲート、出力ゲート、忘却ゲートなどを用いて解決した。下記の図がRNNとLSTMの違いである。詳しい解説はLSTMネットワークの概要の記事を見てください。
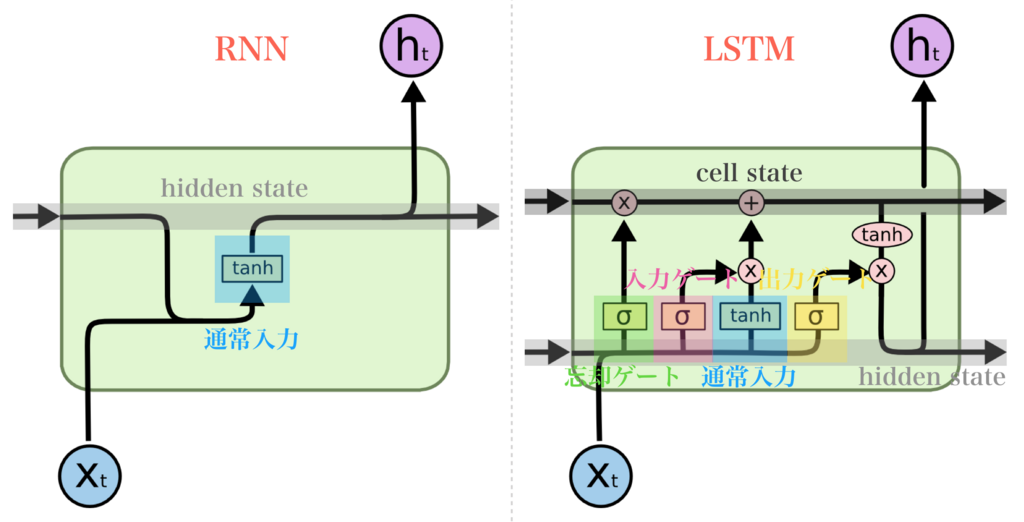[colah's blog:Understanding LSTM Networks](http://colah.github.io/posts/2015-08-Understanding-LSTMs/)から図の引用
sigmoid関数の出力は、0.0~1.0となり、データをどれだけ通すかという割合として考えられるため、ゲートとして使う場合が多い。一方、tanh関数は-1.0~1.0の値が出力され、情報に対する強弱が表されていると考えられるため、活性化関数として使われる場合が多い。
##LSTMの実装
ある程度LSTMを理解したところで、実際に手を動かしていきます。
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from keras.models import Sequential
from keras.layers.core import Dense, Activation , Dropout
from keras.layers.recurrent import LSTM
from keras.callbacks import EarlyStopping
%matplotlib inline
#prediction_target には、予測したい先のデータを入力
#５分間隔のデータなので、一時間後は12
def _load_data(data, n_prev = 288 , prediction_target = 12):
docX, docY = [] , []
for i in range(len(data)- n_prev-(prediction_target +1)):
docX.append(data.iloc[i:i+n_prev].as_matrix())
docY.append(data.iloc[i+n_prev+prediction_target ].as_matrix())
alsX = np.array(docX)
alsY = np.array(docY)
return alsX , alsY
#n_prevの数とcreate_modelのlenght_of_sequencesの値は同じにすること
#_n_prevは予想に用いるデータ量の指定。
#今回は５分間隔のデータで一日分のデータを使って予測するので288
def train_test_split(df, test_size , n_prev=288):
ntrn = round(len(df) * (1-test_size))
ntrn = int(ntrn)
X_train , y_train = _load_data(df.iloc[0:ntrn] , n_prev)
X_test , y_test = _load_data(df.iloc[ntrn:] , n_prev)
return (X_train , y_train), ( X_test, y_test)
#length_of_sequences : 過去何回分を参照して予測するか
def create_model(in_out_neurons , hidden_nurous , lenght_of_sequences):
model = Sequential()
model.add(LSTM(hidden_nurous, batch_input_shape=(None, lenght_of_sequences,\
in_out_neurons), return_sequences = False))
model.add(Dropout(0.5))
model.add(Dense(in_out_neurons))
model.add(Activation('linear'))
model.compile(loss='mean_squared_error' , optimizer='adam',)
return model
df = pd.read_csv('csvファイル名')
(X_train , y_train) , (X_test, y_test) = train_test_split(df, 0.2)
# LSTMはバッチサイズの整数倍にしないと学習しないらしいのでリサイズ
BATCH_SIZE = 32
X_train = X_train[len(X_train) % BATCH_SIZE:]
y_train = y_train[len(y_train) % BATCH_SIZE:]
X_test = X_test[len(X_test) % BATCH_SIZE:]
y_test = y_test[len(y_test) % BATCH_SIZE:]
#X_trainの形はnumpyの３次元配列である必要があります。以下の形
array([[[1, 0, 1, 1, 0],
[2, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
model = create_model(5 ,300,300)
#patience，何回連続して、lossが変わらなかったら学習をやめるか
#なので，patience=10だとlossが10回連続して変わらなかったら，学習が終了することになる．
early_stopping = EarlyStopping(monitor='val_loss', mode='auto', patience=20)
history = model.fit(X_train, y_train, batch_size=32, epochs=13, validation_split=0.1, callbacks=[early_stopping])
#modelの保存
model.save_weights('model/適当な名前.hdf5')
#予想
pred_data = model.predict(X_test)
#結果の出力
plt.plot(y_test , label = 'test')
plt.plot(pred_data , label = 'predict')
plt.legend(loc='upper left')
plt.show()
##結果
テストデータ600を与え.predictを行った結果が以下である。
今回は、グラフの100あたりの跳ね上がりを捉えることを目標としているので、イマイチな結果となった。250くらいのところは捉えてはいるが、数の伸びをとらえることができていない。
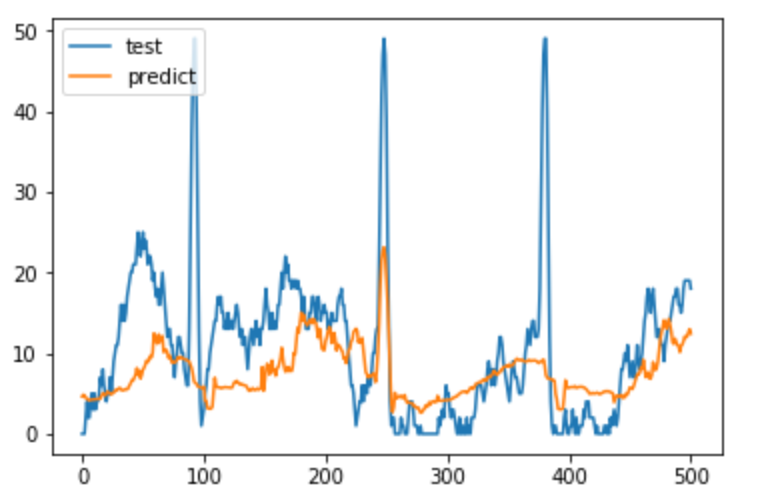
##考察
うまくいかなかった理由は３つあると考える。epochs数が少ない、正規化をしていない。参照しているデータ期間が短い、LSTMレイヤーを多層化するの３つである。
epochs数に関しては、今回はふれないでおく。
次に、正規化である。正規化に関してはすぐにできそうなので、やってみた。このとき、活性化関数はsigmoid関数にする。
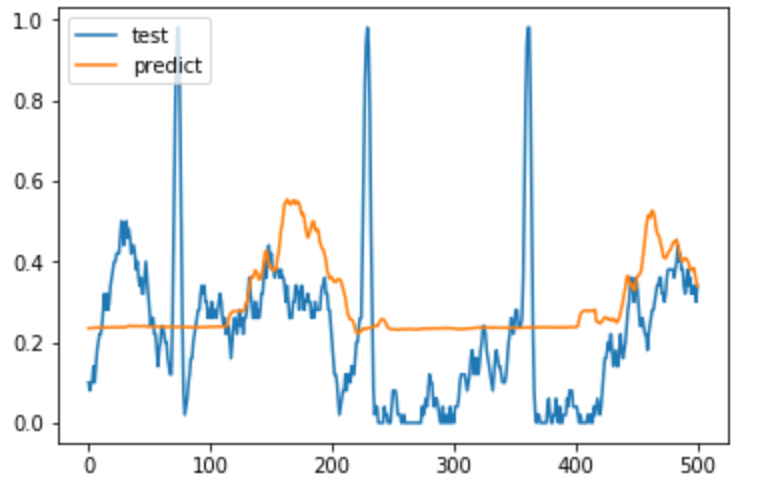
あれ？悪くなってる。どうやら正規化しても今回はうまくいかないみたい。理由はわかならないので、わかる方教えてください。
次に、参照する期間を伸ばしてみたがあまり変わらなかった。
最後に、LSTMレイヤーを増やしてやってみた。
1層よりはよくなった。
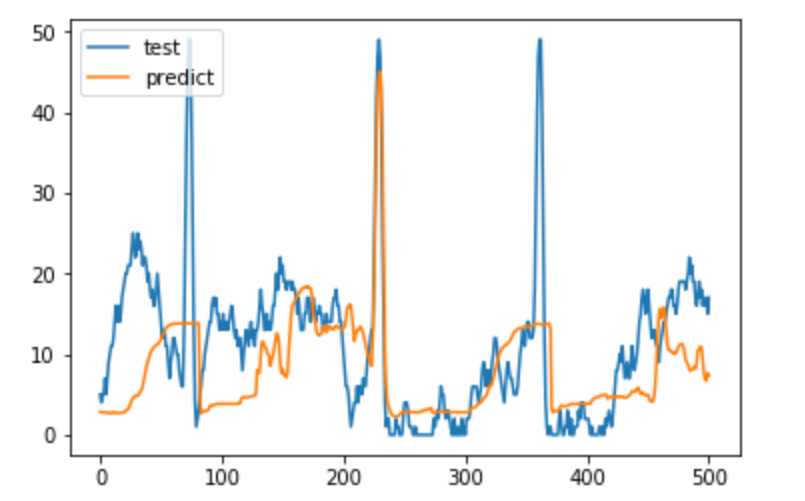
##ワンステップ遅れる
この記事のコードでは修正されているが、予測結果が以下の図のように1ステップ前のデータを次のステップで表示しているみたいになることがある。これは、入力データが間違っているので、プログラムが間違えていないかよく考えてください。そして、おわかりだと思うが日本語の記事は信用しないでください。ある記事を参考にして行った結果が以下です。
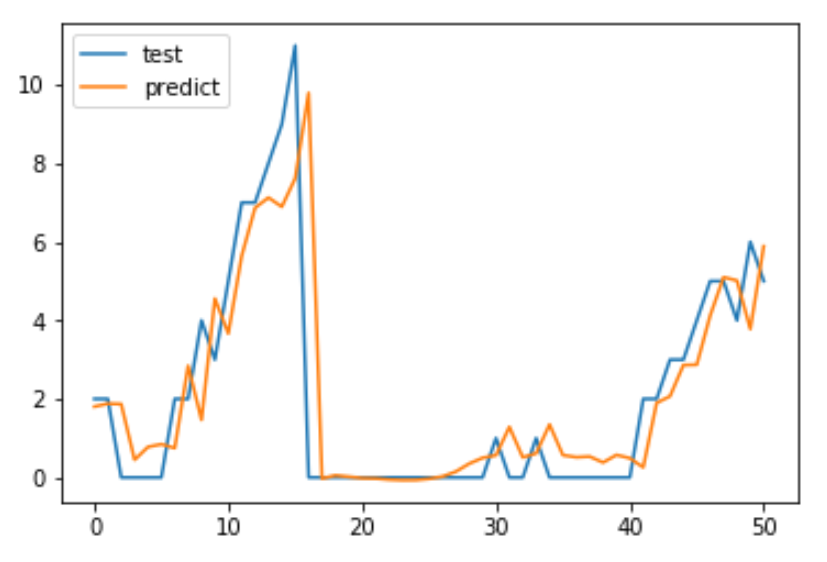
##まとめ
Sin波を捉えることは、LSTMを1層にするだけで十分予測できるが、少し複雑なモデルになると、データ期間を増やしたり、LSTMレイヤーを多層化する必要があると考えられる。
最後になりますが、学習時間を短くするために基本的にepoc数は全部１０程度にしています。
次回は、予測する先(30分先）などを変更することでどう精度が変わっていくかの記事を書く予定です。