【A/Bテスト】誤差の伝搬を理解する【デルタ法、bootstrap法】

概要

近年では新しいサービスをリリースする際にはA/Bテストを実施することが多い。
A/Bテストの集計時には有意差検定をはじめとした統計学の知識が必要とされることが多々ある。
その中でも誤差の伝搬法則を理解するのはとても重要だ。
この記事では誤差の伝搬法則（デルタ法）を用いた誤差の求め方を紹介する。
また、他の手法としてbootstrap法を紹介する。

急に誤差の伝搬と聞いてもなんのことなのか、何が重要なのかわからないと思うので、順番に説明する。

誤差の伝搬とは

適当な例として長方形の面積を求めることを考える。
横の長さXは20cmで誤差3cm、縦の長さYは10cmで誤差1cmとする。
この時面積の誤差はいくらになるだろうか？
面積の値は$10*20=200$とすぐに求まるが、面積の誤差と聞かれてもぱっとはわからないと思う。
この問題を特にはX、Yの誤差が面積XYにどのように"伝搬"するかを考える必要がある。

わかりやすくX、Yの誤差をそれぞれ$E_X, E_Y$とおくと、

X=20,E_{X}=3\\
Y=10,E_{Y}=1\\ 

と表せる。
実は面積$S=XY$の誤差はこれらを使って

\sqrt{(YE_{X})^2+(XE_{Y})^2} = \sqrt{(10*3)^2+(20*1)^2}\\
\approx 6

と表せる。
なぜこのように表せるのだろうか？
また、面積のように二つの変数の積だけでなく和や差、割り算した場合はどうなるだろうか？

A/Bテストとメトリクス

先ほどの面積の例だけだとその重要性がしっくりこないかもしれない。
そこで、数式を計算する前に誤差伝搬の重要性をもう少し具体的に考える。

例えばECサイトやアプリのログを集計したり、新しい施策の効果をみるためにA/Bテストを行なったとする。
そこではclick数をpv数で割ったCTR (Click Through Rate)や、cv数（購入数）をpvで割ったCVR (Conversion Rate)などのメトリクスを計算することがあるだろう。
これらの量で分母、分子がそれぞれ誤差を持っていた場合、当然割り算の誤差の伝搬を計算する必要がある。
他にも「1ユーザーあたりの◯◯数」みたいのを計算するときはだいたい割り算だ。

また、A/Bテストのように別の実験バケットを切って有意差を測定するようなケースでも差や割り算が必要となる。
例えば、介入群とコントロール群の有意差を見たいとしよう。
それぞれの実験群におけるメトリクスの値をそれぞれ$Y_t, Y_c$とおくと、その差は

\Delta = Y_t - Y_c

となる。
t検定を行いたい場合はこの量を分散

var(\Delta) = var(Y_t - Y_c) = var(Y_t) + var(Y_c)

で割って標準正規分布（サンプル数が少ない場合はt分布）を作ることで検定を行える。
（差の分散はここの分散の和になることに注意）
つまり、

t = \frac{\Delta}{\sqrt{var(\Delta)}}

を計算すれば良い。（これをt値と呼ぶ）
また、％の差分と呼ばれる

\Delta\% = \frac{\Delta}{Y_c}

のような値を計算する場合にも割り算の統計誤差を計算する必要がある。
このケースをもう少しだけ一般化してみる。
２つのメトリクス

X = M_{X} + E_{X} \\
Y = M_{Y} + E_{Y}

があり、M、Eをそれぞれ平均値と統計誤差と考える。
この時

\frac{X}{Y}

の誤差はどのように計算できるだろうか？
このように、誤差の伝搬はさまざまな状況で重要となる。

方法1: デルタ法（誤差伝搬の法則）

一般式

二変数X、Yを使ってある関数f(X, Y)が定義されるとする。
X、Yが真の値$(x_{true},y_{true})$をとる時、$f(x_{true},y_{true})$もまた真の値をとるはずだ。
ここで、X、Yのj番目の測定値を$(x_j,y_j)$、真の値からの誤差を$(\Delta x_j,\Delta y_j)$とおく。
すると、j番目の真のfの値は

f_j(x_{true}, y_{true}) = f(x_{j} +\Delta x_j , y_{j} +\Delta y_j) \\
     = f(x_j, y_{j})+\frac{\partial f}{\partial x}\Delta{x_j} + \frac{\partial f}{\partial y}\Delta{y_j} 

となる。二項目への変形でテーラー展開を用いた。
さらに変形して

f_j(x_{true}, y_{true}) - f(x_j, y_{j}) = \frac{\partial f}{\partial x}\Delta{x_j} + \frac{\partial f}{\partial y}\Delta{y_j} 

となる。
この式の左辺は真のfと測定値から計算したfの差を表しているため、これを$\Delta f_j$と置く。
fの統計誤差を知りたいので$\Delta{f}$の二乗の期待値を計算すると

\frac{1}{n}\Sigma_{j=1}^n(\Delta {f_j}^2) = \frac{1}{n}(\Sigma(\frac{\partial f}{\partial x}\Delta{x_j})^2 + \Sigma(\frac{\partial f}{\partial y}\Delta{y_j})^2 +  2\Sigma\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}\Delta{x_j}\Delta{y_j})

ここで$\Delta f, \Delta x, \Delta y$の期待値をそれぞれ$E_f, E_x, E_y$とおき、$\Delta x, \Delta y$の共分散（covariant）を$E_{xy}$とおく。
すると、

E_f = \sqrt{(\frac{\partial f}{\partial x}E_{x})^2 + (\frac{\partial f}{\partial y}E_{y})^2 +  2\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}E_{xy}}

となり、さらにX,Yが独立、あるいは無相関の場合は$E_{xy}=0$となるため

E_f = \sqrt{(\frac{\partial f}{\partial x}E_{x})^2 + (\frac{\partial f}{\partial y}E_{y})^2 }

となる。これを誤差の伝搬法則やデルタ法と呼ぶ。

補足
自分はこの記事を書き始めるまで誤差の伝搬法則とデルタ法を別の手法だと思っていたが、どうやら同じものらしい。
調べてみると、統計の分野ではデルタ法と呼ばれ、数値計算の分野だと誤差の伝搬法則と呼ばれるみたいだ。
機械学習やIT関連の論文だとデルタ法と書くのが主流なのかな？
でもニューラルネットワークで使われる「誤差の逆伝搬」は「逆デルタ法」なんて言わないよね。不思議。

割り算の場合

$f(X,Y)=X/Y$とおけばいい。
微分は

\frac{\partial}{\partial X} (\frac{X}{Y}) = \frac{1}{Y} \\
\frac{\partial}{\partial Y} (\frac{X}{Y}) = -\frac{X}{Y^2} \\

となるので、デルタ法の式に代入すると

E_f = \sqrt{(\frac{1}{Y}E_{x})^2 + (\frac{X}{Y^2}E_{y})^2 -2\frac{X}{Y^3}E_{xy}}\\

が導ける。もしXとYが無相関であれば

E_f = \sqrt{(\frac{1}{Y}E_{x})^2 + (\frac{X}{Y^2}E_{y})^2 }\\

割り算の形になってるメトリクスや上で出てきた%の差分などはこの式を使えば統計誤差が計算できる。

掛け算の場合

$f(X,Y)=XY$とおけばいい。
微分は

\frac{\partial}{\partial X} (XY) = Y \\
\frac{\partial}{\partial Y} (XY) = X \\

となる。XYの相関項を無視してデルタ法の式に代入すると

E_f = \sqrt{(Y E_{x})^2 + (X E_{Y})^2)} \\

となり、最初の長方形の例で用いた式が導けた。

和、差の場合

$f(X,Y)=X\pm Y$とおけばいい。
微分は

\frac{\partial}{\partial X} (X\pm Y) = 1 \\
\frac{\partial}{\partial Y} (X\pm Y) = \pm 1 \\

となる。XYの相関項を無視してデルタ法の式に代入すると

E_f = \sqrt{E_{x}^2 \pm E_{Y}^2} \\

となる。
この式は単純なのでこれくらいは丸暗記しておくと便利かもしれない。

他にも指数が出てきたり3変数以上になったりしても、同じ方法で式が導ける。
参考：http://www.tagen.tohoku.ac.jp/labo/ishijima/gosa-03.html

方法2: bootstrap法

デルタ法を使えば原理上どんなメトリクスでも計算できるが、裏を返せばメトリクスごとにあらかじめ式を計算しておく必要がある。
例えば欲しいメトリクスが複数あるとして、$XY, X/Y, X^2/Y, exp(Y)/XY$ などメトリクスの数だけ上記の式を計算する必要があり
面倒だ。
ここではもう一つbootstrap法という方法を紹介する。
この方法はデルタ法と比べると計算コストがかかるが、どんなメトリクスでもまったく同じ方法で誤差の計算ができる。

そもそも、統計誤差とは何だろうか？
それは、まったく同じシチュエーションで何度も実験した場合にメトリクスがどれくらいばらつくかということだ。
シミュレーションであれば同じ条件何度も実験を行うことができる。
例えばガウス分布からランダムに値をN回発生させれば、N個のサンプルのばらつきから統計誤差を計算できる。
このような乱数を使ったシミュレーションをモンテカルロ法とかモンテカルロシミュレーションとか呼ぶ。

しかし、現実には実験データは一つのデータサンプルが得られるだけだ。
同じ状況で何度も実験を行うのは実験コスト的に難しかったりするし、そもそも"全く同じ"状況というもを作れないケースも多い。

そこで、bootstrap法を使う。
bootstrapでは同一の分布から重複を許してランダムにサンプルを抽出することで、擬似的にモンテカルロ法と同じような状況を作り出す。
（実際bootstrap法はモンテカルロ法の1種と紹介されてたりもする）

この説明だけだと意味がわからないと思うので、具体例を出す。
例えば、以下の5人(A-Eさん)の購入金額のデータから、ユーザーごとの平均購入金額とその誤差を求めたいとする。

A 1200 円
B 1000 円
C 800 円
D 900 円
E 1100 円
平均 1000円

平均値の分散は実データのばらつきから標準偏差を計算し、それをサンプル数で割れば求まる。
標準誤差というやつだ。

StdErr = \frac{\sigma}{\sqrt{N}}

これをbootstrapで計算してみよう。
A-Eさんの中からランダムに"重複を許して"5人選ぶ。
すると例えばこんな感じになるだろう。

E 1100 円
B 1000 円
A 1200 円
D 900 円
E 1100 円
平均 1300円

"重複を許している"というのがポイントで、上の例だとEさんは二回選ばれているが、Cさんは一回も選ばれていない。
平均値も元々の値と微妙に違う値となっている。
この処理をN回行うと、N通りの平均値が計算できるはずだ。
このときの平均値のばらつきは統計的にばらつくはずなので、これを統計誤差として採用するのだ。
Nはbootstrapの回数にあたるわけだが、例えば100回とか200回とか行う。

この方法を使えば、「ユーザーごとの◯◯」にあたるメトリクスはすべて同じ方法で求めることができる。
つまり、デルタ法のようにメトリクスごとに計算式が変わることがない。
デメリットはさきほど述べたように、復元抽出をN回行うという計算コストがかかるということだ。

どちらを採用するかは状況によるが、計算コストに問題がないのであれば個人的にはbootstrap法の方が好きだ。
また、両方計算して本当に統計誤差の値が同じになるかというチェックも、集計の初期段階やA/Aテストでは重要だと個人的に思う。

まとめ

• ログやA/Bテストの集計において、誤差の伝搬はとても大事
• 誤差の伝搬法則（デルタ法） を使えば、さまざまなメトリクスの統計誤差を計算できる
• 復元抽出を用いたbootstrap法という方法もある
• どちらを使うかは計算コストや求めたいメトリクスを考慮して考えるべし
• 両方計算してみて同じになるかチェックするのも大事

補足：テーラー展開は1次まででいいの？

デルタ法の説明で当然のようにテーラー展開を1次で打ち切っていた。
しかし、これはあくまで近似なので「1次で打ち切っていいのか？」という疑問がある人がいるかもしれない。
結論から言うと、ほとんどの場合で問題ない。
なぜかというと、僕たちが考えているような実験の観測値は正規分布のような形をしていることが多いからだ。
正規分布（厳密には正規分布でなくとも）の場合、分布の平均値の真の値（期待値）は上に凸のグラフの頂点である。
そして実際に観測した値はそこから少しずれているものの、直線で十分近似できるからだ。

下の図はイメージだが、わかりやすいように2変数ではなく1変数にしてある。

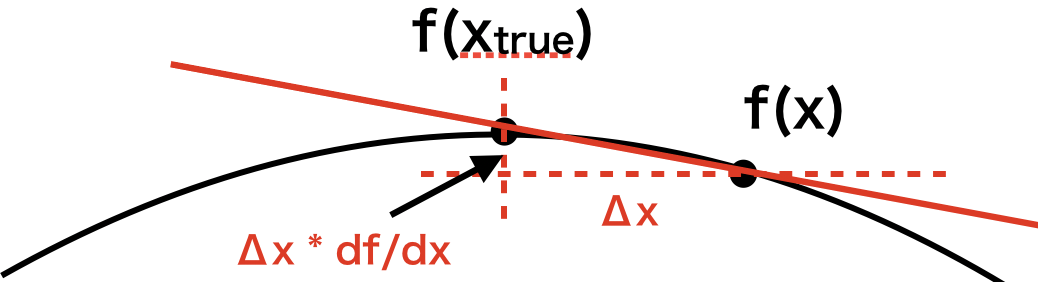
もし平均値周りが変な形をしていれば（めちゃくちゃとんがってて微分不可能とか）、当然この近似は成り立たなくなるが、まぁおおよそ大丈夫だよね？という前提があるわけだ。

A/Bテストの場合、ユーザーごとの平均値などの値をメトリクスとして採用する場合が多い（ユーザーごとのCTRの平均とか）。
平均値の場合はサンプル数が多ければ中心極限定理より分布は正規分布に収束していくため、そのようなメトリクスであればテーラー展開の1次までで十分近似可能(=デルタ法が適用可能)と言えるだろう。

参考文献

webサイト

• 誤差の伝搬法則、デルタ法
  • http://www.tagen.tohoku.ac.jp/labo/ishijima/gosa-02.html
  • https://mathwords.net/gosadenpa
    • 誤差の伝搬法則の数式の導き方が載ってる
  • https://www.szdrblog.info/entry/2018/11/18/154952
    • デルタ法の考え方が載っている

書籍

• A/Bテスト実践ガイド
  • A/Bテスト全般について載っている良書
• 実証のための計量時系列分析
  • bootstrap法について記述あり