この記事は数理物理アドベントカレンダー2018 6日目の記事ですが、技術的な要素多めでお送りします
自動微分とは?
自動微分とはある関数を実装すると、同時にその微分係数を求める関数も実装してくれる技術の事です。
特に合成関数の微分の扱いによってボトムアップ(フォワード)型とトップダウン(リバース)型に分類されます。この節では両者の違いを3つの実数値関数$f, g, h: \mathbb{R} \to \mathbb{R}$の合成関数を例に議論しましょう。
まず二つの場合$f \circ g: x \mapsto f(g(x))$を考えます。$f$の$x$における微分係数を$f^\prime(x)$のように書くとすると合成関数の微分の公式より、
$$
(f \circ g)^\prime(x) = f^\prime (g(x)) g^\prime (x)
$$
あるいは引数を省略して以下のように書けます
$$
(f \circ g)^\prime = (f^\prime \circ g) \cdot g^\prime
$$
ただし "$\cdot$"はかけ算$(f \cdot g)(x) = f(x)g(x)$とします。これを再帰的に適用していけば任意の有限回の関数合成に対して微分係数を計算することが出来ますが、「前」から評価していくか「後」から評価していくかの自由度があります。つまり3つの合成関数$f \circ g \circ h: x \mapsto f(g(h(x)))$に対して以下の二通りの評価順序がありえます:
$$
\begin{align}
(f \circ g \circ h)^\prime &= (f \circ (g \circ h))^\prime \\
&= (f^\prime \circ g \circ h) \cdot (g\circ h)^\prime \\
&= (f^\prime \circ g \circ h) \cdot (g^\prime \circ h) \cdot h^\prime \\
(f \circ g \circ h)^\prime &= ((f \circ g) \circ h)^\prime \\
&= ((f\circ g)^\prime \circ h) \cdot h^\prime \\
&= ((f^\prime \circ g) \cdot g^\prime) \circ h ) \cdot h^\prime
\end{align}
$$
前者のタイプをボトムアップ型、後者のタイプをトップダウン型と呼びます。ボトムアップ型の方がきれいな形をしていますし、$h^\prime$から順番に評価していけばいいので簡単ですが、実はトップダウン型も一度$f(g(h(x))$を評価した時の値を覚えているとまず$f^\prime(g(h(x))$を計算し、$f^\prime(g(h(x))g^\prime(h(x))$を計算し、と順に簡単に計算することができます。一般の計算に対しても同じように計算の過程で得られた中間の値を保持することによってトップダウン型の自動微分が実行できますが、この記憶領域が個々の計算を頂点としたグラフ(実際にはDirected acyclic graph (DAG))になるので計算グラフと呼ばれる構造を管理することになります。
ここでは1次元で説明したのでわかりにくいですが、この二つの方法は引数と値の次元が変化した時の計算量が異なるため、適用する問題にあわせてアルゴリズムを選択する必要があります。例えばニューラルネットワーク(NN)の学習における逆誤差伝搬法はトップダウン型自動微分の一種であり、最近の流行により大くの記事で解説されています。NNから離れて見たとき、これは中間変数を覚えておく事によって深い階層を持つ合成関数の微分を高速に計算するための方法であって、引数の次元が値の次元に比べて大きい場合に相性が良いことが知られています。
cagra: tiny calculation graph library
cagra (CAlculation GRAph library)はRust製の計算グラフライブラリです。この節では実装の技術的な話題を扱います。
このライブラリではRustのパーザーであるsynを用いてfunction-style proc_macroで入力をパースする事で計算グラフを構築します。
let mut g = graph!(f64, { // 計算グラフの定義
let q = 1.0; // 初期値 q = 1.0
let p = 1.0; // p = 1.0
let h = square(q) + square(p); // H = q^2 + p^2
});
このユーザの入力に対してgraph!マクロはコンパイル時に以下のようなコードに展開されて実行時にグラフを構築します:
let mut g = cagra::graph::Graph::new();
let q = g.variable("q", 1.0).expect("Duplicated symbols");
let q = q;
g.set_name(q, "q");
let p = g.variable("p", 1.0).expect("Duplicated symbols");
let p = p;
g.set_name(p, "p");
let h__lhs__arg0 = q;
let h__lhs = g.square(h__lhs__arg0);
let h__rhs__arg0 = p;
let h__rhs = g.square(h__rhs__arg0);
let h__lhs = h__lhs;
let h__rhs = h__rhs;
let h = g.add(h__lhs, h__rhs);
g.set_name(h, "h");
ちなみにこのマクロを実装するのに以下の記事が非常に参考になりました:
グラフの扱いはpetgraphというC++のBoost.GraphやPythonのnetworkxに似たライブラリがあるのでこれを使います。
グラフの各頂点には上でいう$f(g(h(x))$と$f^\prime(g(h(x))$に対応してvalueとderivという量をもたせます。初期化の段階でグラフは次の図のようになっています:
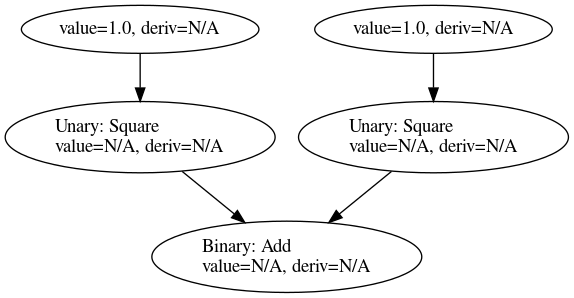
デバッグ用のDOT出力なのでちょっと見辛いですが、左上がq,右上がpでそれらをSquareという単項演算子が2乗して最後にAddという二項演算子で足しあわされています。
続いてハミルトニアンを評価します
let h = g.eval_value(h)?;
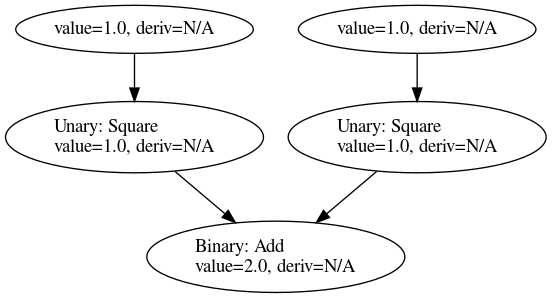
これで順方向にグラフを評価した時の値を各頂点に記憶させる事ができました。ちょうどエネルギーを測ったことになるので、エネルギーが増減してないかのチェックにもなります。最後にこの値を使って微分係数を評価しましょう。
g.eval_deriv(h)?;
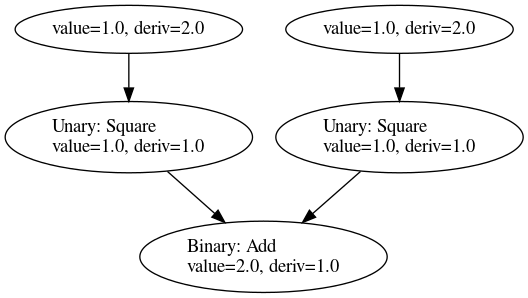
この関数は実際にはハミルトニアンhの頂点からグラフを探査して順に微分係数を評価しています(なので開始の頂点をあげている)。
このように順方向の評価と逆方向の微分係数の評価を順番に繰り返す操作はちょうどハミルトン系の運動方程式を解く操作と似ていますね。次の節は実際に単振動系の初期値問題をcagraを使って解いてみます。
単振動系のシミュレーション
ハミルトニアンを自動微分して時間発展を計算するソフトウェアは先日の記事gloss: 動かして遊んで学ぶHaskellでも紹介されているhamiltonなどがあります。ハミルトニアンはNNと同様に引数の次元が値の次元(必ず1になる)より大きくなるのでトップダウン型の自動微分が向いています。
cagraを用いて $H(q, p) = q^2 + p^2$の単振動系を1次のシンプレクティック法で解いていきます。1次のシンプレクティック法は時刻$t$における座標、運動量をそれぞれ$q^{(t)}, p^{(t)}$と書くと、
$$
\begin{align}
p^{(t+1)} &= p^{(t)} - dt \frac{\partial H}{\partial p}(q^{(t)}, p^{(t)}) \\
q^{(t+1)} &= q^{(t)} + dt \frac{\partial H}{\partial p}(q^{(t)}, p^{(t+1)})
\end{align}
$$
のように簡単な更新で記述できます。この微分係数の計算を順次$q, p$を更新しながらやっていきます。
# [macro_use]
extern crate cagra;
use failure::Error;
fn main() -> Result<(), Error> {
let mut g = graph!(f64, { // 計算グラフの定義
let q = 1.0; // 初期値 q = 1.0
let p = 1.0; // p = 1.0
let h = square(q) + square(p); // H = q^2 + p^2
});
let q = g.get_index("q");
let p = g.get_index("p");
let h = g.get_index("h");
let dt = 0.01;
println!("t,E,q,p"); // csv header
for t in 0..1000 {
let e = g.eval_value(h)?; // ハミルトニアンを評価
g.eval_deriv(h)?; // 自動微分で微分係数を評価
let vp = g.get_value(p)?;
let hq = g.get_deriv(q)?;
g.set_value(p, vp - dt * hq)?; // 運動量(p)の更新
g.eval_value(h)?; // 運動量を更新した状態でハミルトニアンを評価
g.eval_deriv(h)?; // 自動微分で微分係数を評価
let vq = g.get_value(q)?;
let hp = g.get_deriv(p)?;
g.set_value(q, vq + dt * hp)?; // 座標(q)の更新
println!("{:.09},{:.09},{:.09},{:.09}", dt * t as f64, e, vq, vp); // CSVに出力
}
Ok(())
}
Rustの文法は雰囲気で理解してください(無茶振り)。
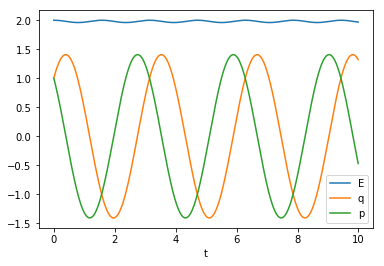
これはCSVを標準出力に生成するので、matplotlibを用いて可視化したものが以下の図です
エネルギーが少し振動しているような気がしますが、単振動がちゃんと計算できていますね!これでハミルトニアンを記述するだけで運動方程式の初期値問題を解くことができました!