More than 5 years have passed since last update.

@lotzin

株式会社FOLIO

gloss: 動かして遊んで学ぶHaskell

Last updated at 2018-11-10Posted at 2018-11-10

1 / 53

自己紹介

趣味はHaskellと人工知能
普段は半蔵門で働くエンジニア

Twitter: @lotz84_（質問があればこちらまで）
GitHub: @lotz84
Qiita: @lotz

Haskell入門のあとにありがちなパターン

by Twitterを巡回していてわかったHaskell初心者が躓きやすいポイント8つ

(lotz調べ)

もっと想像力を刺激するような
実装例が必要なのでは？

gloss: Painless 2D vector graphics, animations and simulations.

出展: glossではじめるグラフィック描画 :: Haskell入門の次に読む記事

gloss

2Dグラフィックを簡単に描画できるライブラリ

アニメーション
シミュレーション
マウスやキーボードのイベント処理

にも対応

目に見えるものがすぐに作れるので楽しい！✌('ω'✌ )三✌('ω')✌三( ✌'ω')✌

今回の目標
Twitterで「glossで作ってみた」報告が
たくさん投稿される

Hello World

gloss: Hello World

import Graphics.Gloss

main :: IO ()
main = display inWindow white message
  where
    inWindow = InWindow "Haskell Day 2018" (640, 480) (100, 100)
    message = text "Hello World"

display

与えられた図形を単純に描画する関数

display :: Display -- 描画モード
        -> Color   -- 背景色
        -> Picture -- 描画する図形
        -> IO ()

-- ウィンドウの表示モードを表す型
data Display = InWindow String (Int, Int) (Int, Int)
             | FullScreen

-- 色を表す型
data Color = ...

-- 図形を表す型
data Picture = ...

glossにおける重要な４つの関数

-- 与えられた図形を単純に描画する関数
display :: Display -- 描画モード
        -> Color   -- 背景色
        -> Picture -- 描画する図形
        -> IO ()


-- 時間変化を伴う図形（アニメーション）を描画する関数
animate :: Display            -- 描画モード
        -> Color              -- 背景色
        -> (Float -> Picture) -- 経過時間を受け取って図形を返す関数
        -> IO ()


-- モデルの時間発展をシミュレーションして描画する関数
simulate :: Display            -- 描画モード
         -> Color              -- 背景色
         -> Int	               -- 1秒あたりのステップ数
         -> model              -- モデルの初期値
         -> (model -> Picture) -- モデルから図形に変換する関数
         -- ビューポートと前ステップからの経過時間を受け取ってモデルを発展させる関数
         -> (ViewPort -> Float -> model -> model)
         -> IO ()


-- キーボードやマウスなどの入力イベントを処理してゲームを描画する関数
play :: Display	-- 描画モード
     -> Color   -- 背景色
     -> Int     -- 1秒あたりのステップ数
     -> world   -- ワールドの初期値
     -> (world -> Picture)        -- ワールドから図形に変換する関数
     -> (Event -> world -> world) -- イベントを元にワールドを更新する関数
     -> (Float -> world -> world) -- 1ステップの経過時間を受け取ってワールドを発展させる関数
     -> IO ()

Picture

Line

線分

line :: [(Float, Float)] -> Picture

Circle

円

circle :: Float -> Picture

circleSolid :: Float -> Picture

Rectangle

長方形

rectangleWire :: Float -> Float -> Picture

rectangleSolid :: Float -> Float -> Picture

Text

文字列

text :: String -> Picture

ただし、フォントの指定や日本語の表示ができない

Pictureを変形する

Translate

図形を移動する

translate :: Float   -- x座標の移動量
          -> Float   -- y座標の移動量
          -> Picture -- 移動させたい図形
          -> Picture

glossの座標系

Scale

拡大縮小させる

scale :: Float -> Float -> Picture -> Picture

Hello World 2

「Hello World」の文字列全体を表示する

import Graphics.Gloss

main :: IO ()
main = display inWindow white message
  where
    inWindow = InWindow "Haskell Day 2018" (640, 480) (100, 100)
    message = translate (-160) 0 . scale 0.5 0.5 $ text "Hello World"

Rotate

図形を時計回りに回転させる。角度は度数法で指定する

rotate :: Float -> Picture -> Picture

Color

図形の色を変える

color :: Color -> Picture -> Picture

black, white, red, green, blue  :: Color

makeColor :: Float -- Red
          -> Float -- Green
          -> Float -- Blue
          -> Float -- Alpha
          -> Color

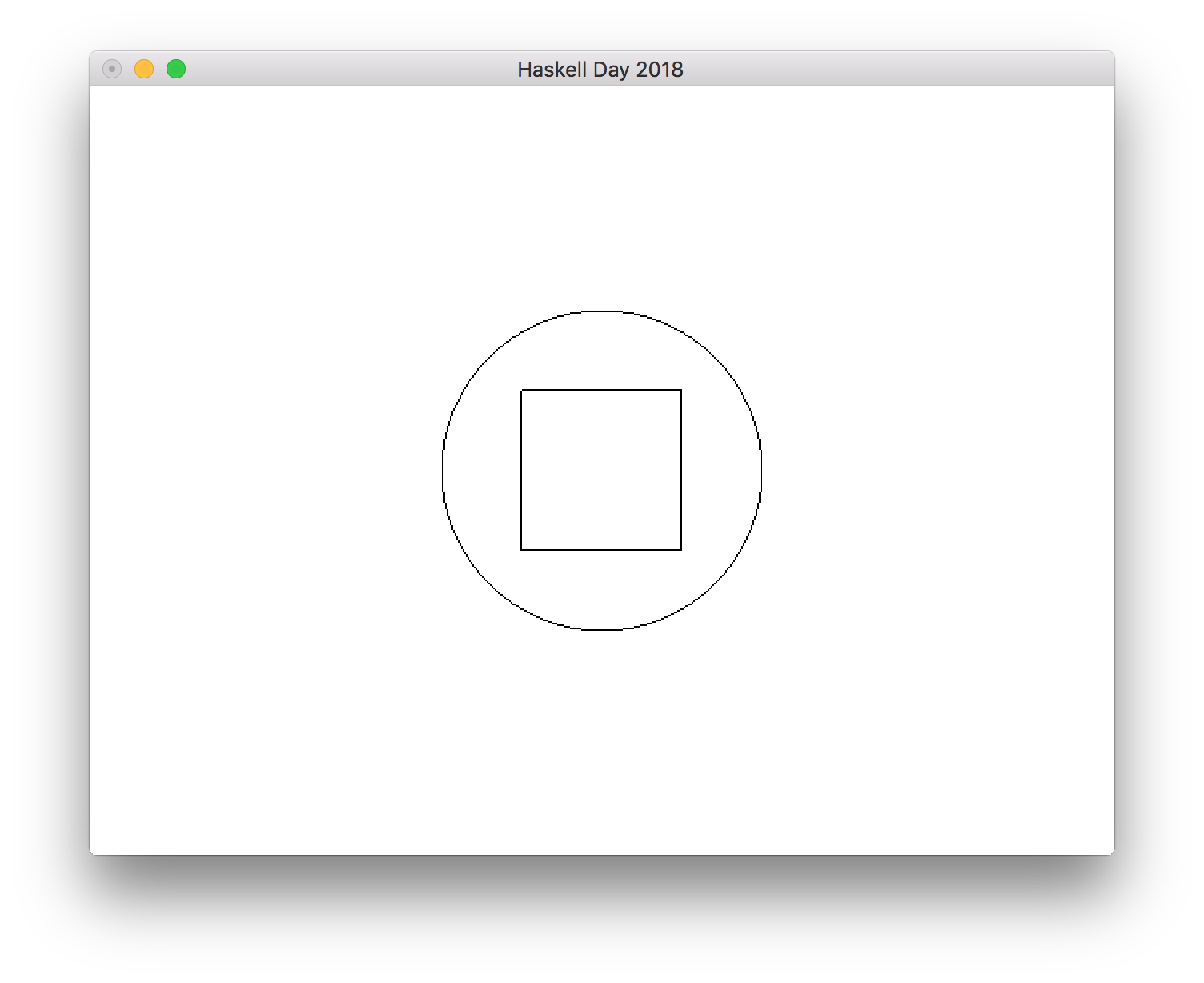
Monoid

PictureはMonoidのインスタンスとなっている
図形を合成するときはモノイドの演算を用いる

circle 50 <> rectangleWire 50 50

物理シミュレーション

二重振り子のシミュレーション

simulateの考え方

-- モデルの時間発展をシミュレーションして描画する関数
simulate :: Display            -- 描画モード
         -> Color              -- 背景色
         -> Int	               -- 1秒あたりのステップ数
         -> model              -- モデルの初期値
         -> (model -> Picture) -- モデルから図形に変換する関数
         -- ビューポートと前ステップからの経過時間を受け取ってモデルを発展させる関数
         -> (ViewPort -> Float -> model -> model)
         -> IO ()

以下の3つの設計が重要

状態を表す抽象的なモデル
モデルの時間発展を記述する関数
モデルを視覚的な情報に変換する関数

モデルと時間発展

二重振り子における状態

運動方程式

(m_1 + m_2)l_1\frac{d^2\theta_1}{dt^2} + m_2l_2\frac{d^2\theta_2}{dt^2}\cos(\theta_1 - \theta_2) + m_2l_2\left(\frac{d\theta_2}{dt}\right)^2\sin(\theta_1 - \theta_2) + (m_1 + m_2)g\sin\theta_1 = 0

l_1l_2\frac{d^2\theta_1}{dt^2}\cos(\theta_1 - \theta_2) + l^2_2\frac{d^2\theta_2}{dt^2} - l_1l_2\left(\frac{d\theta_1}{dt}\right)^2\sin(\theta_1 - \theta_2) + gl_2\sin\theta_2 = 0

この連立方程式を二つの加速度について解けば良い…

参考: 二重振り子 - Wikipedia

hamilton

ハミルトン力学と自動微分を利用して一般化座標系における物理をシミュレーションしてくれるライブラリ

-- m次元のデカルト座標、n次元の一般化座標を持つ系
data System m n = ...

-- 系を作成する関数
mkSystem' :: (KnownNat m, KnownNat n)	 
          => R m                        -- 各デカルト座標系における慣性（質量）
          -> (Vector n a -> Vector m a) -- 一般化座標系からデカルト座標系への変換
          -> (Vector m a -> a)          -- デカルト座標系における位置エネルギー
          -> System m n

-- 相空間の状態を系に従って発展させる関数
stepHam :: (KnownNat m, KnownNat n)
        => Double     -- 微小時間
        -> System m n -- 物理系
        -> Phase n    -- 相空間の状態
        -> Phase n

data Phase n = Phs
  { phsPositions :: R n -- 一般化座標
  , phsMomenta   :: R n -- 一般化運動量
  }

二重振り子におけるSystem

pendulum :: System 4 2
pendulum = mkSystem' mass transform potential
  where
    mass = vec4 1 1 1 1                                     -- 慣性
    transform (V.toList -> [t1, t2]) =                      -- 角度から重りのデカルト座標への変換
      let (x1, y1) = (sin t1, -cos t1)
          (x2, y2) = (sin t1 + sin t2, -(cos t1 + cos t2))
       in fromJust $ V.fromList [x1, y1, x2, y2]
    potential (V.toList -> [_, y1, _, y2]) = y1 + y2        -- 位置エネルギー（y座標の値の合計）

二重振り子の描画

type Model = Phase 2

draw :: Model -> Picture
draw (Phs qs _) =
  let radian   = 180 / pi
      t1       = realToFrac $ qs <.> vec2 1 0
      t2       = realToFrac $ qs <.> vec2 0 1
      l        = 100                                    -- 振り子の見た目の長さ
      stick  = translate 0 (-l/2)  $ rectangleSolid 1 l -- 棒
      weight = translate 0 (-l)    $ circleSolid 10     -- 重り
      (x1, y1) = (l * sin t1, l * (-cos t1))            -- １つ目の振り子の先端位置
      pendulum1 =                   rotate (-t1 * radian) $ stick <> weight
      pendulum2 = translate x1 y1 . rotate (-t2 * radian) $ stick <> weight
   in pendulum1 <> pendulum2

二重振り子のシミュレーション

main :: IO ()
main = simulate inWindow white 24 initModel draw (\_ -> step)
  where
    inWindow  = InWindow "Haskell Day 2018" (640, 480) (100, 100)
    initModel = Phs (vec2 2 2) (vec2 0 0)
    step dt = stepHam (realToFrac dt) pendulum

https://gist.github.com/lotz84/7c784e2fc3c4016960dbe323ae53b4d2

初期値をずらした振り子を50本用意すれば冒頭の動画が作れる
同じ方法でn重振り子も簡単に作れる

コモナドで作るライフゲーム

コモナド

自己関手の圏におけるコモノイド対象
Haskellでは単なる型クラス

class Functor w     => Comonad w where
  extract   :: w a -> a
  duplicate :: w a -> w (w a)

  extend    :: (w b -> a) -> w b -> w a
  extend f = fmap f . duplicate

包まれた値から中身を取り出す extract
包まれた値をさらに包む duplicate

モナド

自己関手の圏におけるモノイド対象
Haskellでは単なる型クラス

class Applicative m => Monad m   where
  pure      :: a -> m a
  join      :: m (m a) -> m a

  (>>=)     :: (a -> m b) -> m a -> m b
  k >>= m = join $ fmap k m

値を包む return
二重に包まれた値を一重にする join

コモナドにまつわる話

コモナドはモナドの圏論的双対
- 有名なモナドの双対
  - Reader ↔ Env
  - Writer ↔ Traced
  - State ↔ Store
Zipperもコモナド
Lensは余状態余モナドの余代数
- つまりStoreコモナドの余代数
画像のフィルタ処理をコモナドで実装できる
- ガウシアンフィルタとか微分フィルタとか

今日はコモナドの詳しい話は割愛します

ライフゲーム

ライフゲームは1970年にイギリスの数学者コンウェイによって考案された
生命の誕生・進化・淘汰のプロセスを再現した簡易的なモデル

平面上に生存セル■と死亡セル□が升目上に並べられており、決められたルールにより時間発展していく

ライフゲームの4つのルール

生

誕生
- 死亡セルに隣接する生存セルがちょうど3つあれば、生存セルとなる
生存
- 生存セルに隣接する生存セルが2つか3つならば、生存セルとなる

死

過疎
- 生存セルに隣接する生存セルが1つ以下ならば、死亡セルとなる
過密
- 生存セルに隣接する生存セルが4つ以上ならば、死亡セルとなる

例: ブロック・ブリンカー・グライダー

ライフゲームのデータ構造

-- | 1点に注目した無限リスト
data Z a = Z [a] a [a]

left, right :: Z a -> Z a
left  (Z (l:ls) c rs    ) = Z ls     l (c:rs)
right (Z ls     c (r:rs)) = Z (c:ls) r rs

ライフゲームのデータ構造

iterate1 :: (a -> a) -> a -> [a]
iterate1 f = tail . iterate f

instance Functor Z where
  fmap f (Z ls c rs) = Z (fmap f ls) (f c) (fmap f rs)

instance Comonad Z where
  -- extract   :: Z a -> a
  extract (Z _ a _) = a

  -- duplicate :: Z a -> Z (Z a)
  duplicate z = Z (iterate1 left z) z (iterate1 right z)

ライフゲームのデータ構造

-- | 1点に注目した無限平面（2重リスト）
newtype Z2 a = Z2 (Z (Z a))

instance Functor Z2 where
  fmap f (Z2 zz) = Z2 (fmap (fmap f) zz)

instance Comonad Z2 where
  -- extract   :: Z2 a -> a
  extract (Z2 zz) = extract (extract zz)

  -- duplicate :: Z2 a -> Z2 (Z2 a)
  duplicate (Z2 zz) = fmap Z2 . Z2 . roll $ roll zz
    where
      roll :: Z (Z a) -> Z (Z (Z a))
      roll zz = Z (iterate1 (fmap left) zz) zz (iterate1 (fmap right) zz)

ライフゲームのデータ構造

True: 生存セル
False: 死亡セル

-- | 注目している点の周りのTrueの数を数える
neighbours :: Z2 Bool -> Int
neighbours (Z2 (Z
  (Z (n0:_) n1 (n2: _):_)
  (Z (n3:_) _  (n4:_))
  (Z (n5:_) n6 (n7: _):_))) =
    length $ filter id [n0, n1, n2, n3, n4, n5, n6, n7]

-- | 注目している点が次のステップで生存するかを判定する
life :: Z2 Bool -> Bool
life z = (a && (n == 2 || n == 3)) || (not a && n == 3)
  where
    a = extract z
    n = neighbours z

-- ライフゲームを時間発展させる
extend life :: Z2 Bool -> Z2 Bool

ライフゲームの描画

wWidth, wHeight :: Num a => a
wWidth  = 640
wHeight = 480

type Model = Z2 Bool

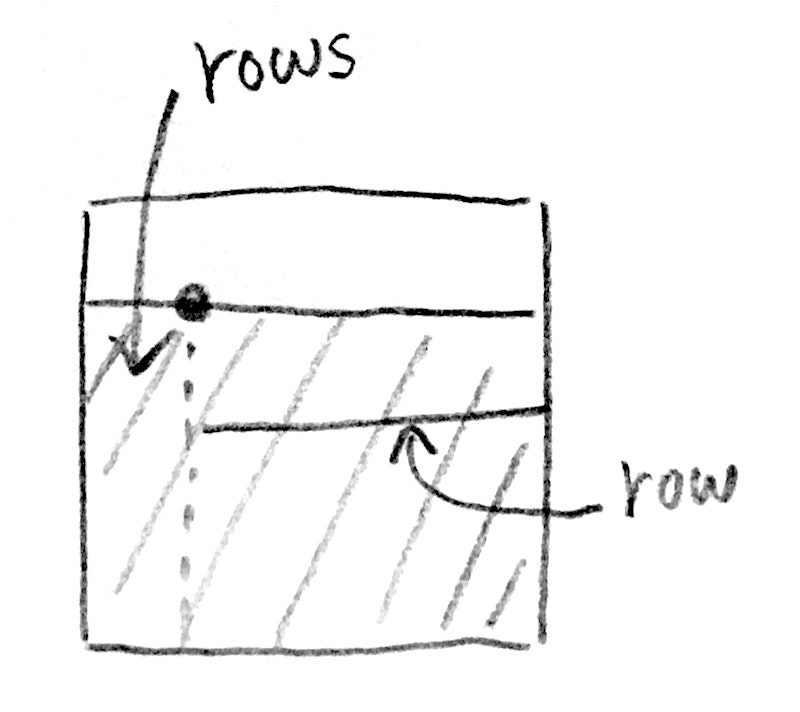
draw :: Model -> Picture
draw (Z2 (Z _ _ rows)) =
  let cSize   = 20 -- セルの大きさ
      -- 基本となるセルの四角形。右下に原点がくる
      cell    = translate (-cSize / 2) (cSize / 2) $ rectangleSolid cSize cSize
      b2c b   = if b then black else white -- Boolから色への変換
      nWidth  = ceiling $ wWidth  / cSize  -- 横方向のセルの個数
      nHeight = ceiling $ wHeight / cSize  -- 縦方向のセルの個数
      cells   = do
        ((Z _ _ row), h) <- zip rows [1..nHeight] -- 縦方向に盤面を走査する
        (b,           w) <- zip row  [1..nWidth]  -- 横方向に行を走査する
        let x = fromIntegral w * cSize - wWidth / 2   -- セルのx座標
            y = wHeight / 2 - fromIntegral h * cSize  -- セルのy座標
            transform = color (b2c b) . translate x y -- セルに施す変形
        pure $ transform cell
   in mconcat cells -- 計算した全てのセルを結合して1つのPictureにする

ライフゲームの実装

toZ :: a -> [a] -> Z a
toZ a xs = Z (repeat a) a (xs ++ repeat a)

toZ2 :: a -> [[a]] -> Z2 a
toZ2 a xss = Z2 $ toZ (toZ a []) (map (toZ a) xss)


main :: IO ()
main = simulate inWindow white 3 initModel draw (\_ _ -> extend life)
  where
    inWindow  = InWindow "Haskell Day 2018" (wWidth, wHeight) (100, 100)
    field = [ " # "
            , "  #"
            , "###"
            ]
    initModel = toZ2 False $ map (map (== '#')) field

https://gist.github.com/lotz84/435630be7ee21cc9b4dfbd004a7cb7fd

遅延評価により描画に必要なデータだけ評価されるのでちゃんと動く
しかし時間がたつにつれ計算量が増えていくのが難点
Z2を平面ではなくトーラス上に実装することはできる？

Graphics.Gloss.Interface.IO

glossの中でIOを使いたい

乱数
ネットワーク通信
セーブデータのファイル出力
FRPライブラリと組み合わせて使いたい
（などなど）

glossのモジュールを眺めてみると…

Graphics.Gloss.Interface.IO

-- モデルの時間発展をシミュレーションして描画する関数
simulateIO :: Display            -- 描画モード
           -> Color              -- 背景色
           -> Int                -- 1秒あたりのステップ数
           -> model              -- モデルの初期値
           -> (model -> IO Picture) -- モデルから図形に変換する関数
           -- ビューポートと前ステップからの経過時間を受け取ってモデルを発展させる関数
           -> (ViewPort -> Float -> model -> IO model)
           -> IO ()

-- キーボードやマウスなどの入力イベントを処理してゲームを描画する関数
playIO :: Display -- 描画モード
       -> Color   -- 背景色
       -> Int     -- 1秒あたりのステップ数
       -> world   -- ワールドの初期値
       -> (world -> IO Picture)        -- ワールドから図形に変換する関数
       -> (Event -> world -> IO world) -- イベントを元にワールドを更新する関数
       -> (Float -> world -> IO world) -- 1ステップの経過時間を受け取ってワールドを発展させる関数
       -> IO ()

Graphics.Gloss.Interface.Pure（比較用）

-- モデルの時間発展をシミュレーションして描画する関数
simulate   :: Display            -- 描画モード
           -> Color              -- 背景色
           -> Int                -- 1秒あたりのステップ数
           -> model              -- モデルの初期値
           -> (model ->    Picture) -- モデルから図形に変換する関数
           -- ビューポートと前ステップからの経過時間を受け取ってモデルを発展させる関数
           -> (ViewPort -> Float -> model ->    model)
           -> IO ()

-- キーボードやマウスなどの入力イベントを処理してゲームを描画する関数
play   :: Display -- 描画モード
       -> Color   -- 背景色
       -> Int     -- 1秒あたりのステップ数
       -> world   -- ワールドの初期値
       -> (world ->    Picture)        -- ワールドから図形に変換する関数
       -> (Event -> world ->    world) -- イベントを元にワールドを更新する関数
       -> (Float -> world ->    world) -- 1ステップの経過時間を受け取ってワールドを発展させる関数
       -> IO ()

例: カオスゲーム

適当な点から始めて多角形の頂点をランダムに選び内分点を取っていくとフラクタル図形ができる（反復関数系）

例えば三角形と中点で内分点を取る操作を繰り返すと シェルピンスキーのギャスケット になる

vertexes :: [Point]
vertexes = [(0, 120), (-160, -120), (160, -120)]

次の点を計算する関数

type Model = [Point]

step :: Model -> IO Model
step [] = pure []                          -- まだ点が無ければ何もしない
step ps@((x, y):_) = do
  gen <- createSystemRandom                -- 乱数のジェネレータを生成
  i   <- uniformR (0, 2) gen               -- ランダムなインデックスを生成
  let (vx, vy) = vertexes !! i             -- ランダムな頂点の座標
  pure $ ((x + vx) / 2, (y + vy) / 2) : ps -- 内分点を計算して追加する

イベントハンドラ

handler :: Event -> Model -> IO Model
-- 最初に左クリックされた点を開始点とする
handler (EventKey (MouseButton LeftButton) Down _ (x, y)) [] = pure $ [(x, y)] 
handler _ model = pure model -- それ以外の時は何もしない

描画処理

draw :: Model -> IO Picture
draw ps =
  let vCircles = map (\(x, y) -> translate x y $ circleSolid 5) $ vertexes
      pCircles = map (\(x, y) -> translate x y $ circleSolid 2) $ ps
   in pure $ mconcat vCircles <> mconcat pCircles

main関数

main :: IO ()
main = playIO inWindow white 24 [] draw handler (\_ -> step)
  where
    inWindow  = InWindow "Haskell Day 2018" (640, 480) (100, 100)

https://gist.github.com/lotz84/492f260bf75588f0eab88b99ee9276d4

まとめ

glossを使えば簡単に2Dグラフィックを扱える
hamiltonを使えば運動方程式も簡単に扱える
コモナドを使えばライフゲームが簡単に作れる
glossにはIOを伴うインターフェースも用意されている

さぁglossで遊びましょう！

ご清聴ありがとうございました

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

gloss: 動かして遊んで学ぶHaskell

自己紹介

Haskell入門のあとにありがちなパターン

もっと想像力を刺激するような実装例が必要なのでは？

gloss: Painless 2D vector graphics, animations and simulations.

gloss

今回の目標Twitterで「glossで作ってみた」報告がたくさん投稿される

Hello World

gloss: Hello World

display

glossにおける重要な４つの関数

Picture

Line

Circle

Rectangle

Text

Pictureを変形する

Translate

Scale

Hello World 2

Rotate

Color

Monoid

物理シミュレーション

二重振り子のシミュレーション

simulateの考え方

モデルと時間発展

hamilton

二重振り子におけるSystem

二重振り子の描画

二重振り子のシミュレーション

コモナドで作るライフゲーム

コモナド

モナド

コモナドにまつわる話

ライフゲーム

ライフゲームの4つのルール

生

死

例: ブロック・ブリンカー・グライダー

ライフゲームのデータ構造

ライフゲームのデータ構造

ライフゲームのデータ構造

ライフゲームのデータ構造

ライフゲームの描画

ライフゲームの実装

Graphics.Gloss.Interface.IO

glossの中でIOを使いたい

Graphics.Gloss.Interface.IO

Graphics.Gloss.Interface.Pure（比較用）

例: カオスゲーム

まとめ

さぁglossで遊びましょう！

ご清聴ありがとうございました

もっと想像力を刺激するような
実装例が必要なのでは？

今回の目標
Twitterで「glossで作ってみた」報告が
たくさん投稿される