[Julia] 行列を高速に更新する

訂正

[2019/03/22] 本文中の LinearIndices(CartesianIndices())p に関する記述は一旦保留とします。
おそらく例2について、意図した結果になりません。追って修正しますが、当該部分の記述とグラフは読み飛ばして頂くようにお願いします。

はじめに

Julia は表現力の豊かな言語で、同じ処理を行うにも、いくつもの書き方があります。

以下のような、行列を更新する計算について、実行時間を調べてみました。

$$W \leftarrow U + \alpha V$$

$U, V, W$ は、同じ寸法の密行列で、要素の型は浮動小数点型 Float64 とします。$U$ と $V$ は壊しません (書き換えません)。$\alpha$ は Float64型のスカラーです。

この計算を行うのに、以下のような方法が考えられます。(なお並列化は考えません)

• 行列の計算
• 行列の要素同士の計算
• 二重ループ
• 単純ループ
  • イテレータ eachindex() を使う
  • イテレータ CartesianIndices() を使う
  • イテレータ LinearIndices(CartesianIndices()) を使う

この他に、

• 対応する BLAS や LAPACK の関数 (があれば。それら)を呼ぶ

という方法もありますが、割愛します ($U$ の値を保存しておいて、BLASの axpy 関数 $y \leftarrow ax + y$ に相当する関数を使うとよさそうです)。

以下に計測結果を紹介しますが、冒頭に実行時間の傾向をまとめておきます。

1. 行列の計算は遅いです。
2. 二重ループは、第1軸を最も内側で回しましょう。
3. イテレータ eachindex(u) や LinearIndices(CartersianIndices(u)) は簡潔に書けて、実行速度も落ちません。

ちなみに、1. と 2. および 3. の前半 eachindex(u)については、Julia Documentation や、過去の記事でも、解説されています。

• Julia Documentation, Perfomance Tips > Access arrays in memory order, along columns
• @bicycle1885 さん Juliaではfor文を使え。ベクトル化してはいけない。

ですが、3. の後半 LinearIndices(CartersianIndices(u)) は、日本語の紹介記事をまだ見たことがありません。

実行環境

Google Colab に興味があるので、Google Colab で実行した結果を、以下に示します。Qiita の記事 Google Colab で Julia を使ってみた の記事の通りに、Julia 1.0 の実行環境を準備しました。GPU は使っていません。

Julia の環境は、以下のようでした。

julia> versioninfo()
Julia Version 1.0.0
Commit 5d4eaca0c9 (2018-08-08 20:58 UTC)
Platform Info:
  OS: Linux (x86_64-pc-linux-gnu)
  CPU: Intel(R) Xeon(R) CPU @ 2.30GHz
  WORD_SIZE: 64
  LIBM: libopenlibm
  LLVM: libLLVM-6.0.0 (ORCJIT, haswell)

この環境を用いて、以下のプログラムを実行した結果を、次のgist に置いておきます。
* https://gist.github.com/hsugawa8651/557a9237653962defeb8f55d9922aedb

参考に、手元の MacBookPro で同じプログラムを実行した結果を示します。
* https://gist.github.com/hsugawa8651/77f0cec335c2ed4b7d11c2db22179552
こちらの実行環境は、以下の通りです。Julia公式ページで配布の Julia 1.1 バイナリを用いました。各例題の末尾にグラフのみ示します。

julia> versioninfo()
Julia Version 1.1.0
Commit 80516ca202 (2019-01-21 21:24 UTC)
Platform Info:
  OS: macOS (x86_64-apple-darwin14.5.0)
  CPU: Intel(R) Core(TM) i5-7267U CPU @ 3.10GHz
  WORD_SIZE: 64
  LIBM: libopenlibm
  LLVM: libLLVM-6.0.1 (ORCJIT, skylake)

例題1

では、具体的に、上の例題を Julia で書いてみます。

行列の計算

Julia は、行列の計算を、そのまま書き表すことができます。

w=u+v*alpha

これを、以下のような、関数として定義しました。

ex1_with_matrix.jl

function ex1_with_matrix(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  w=u+v*alpha
  0
end

行列 u, v, w は、関数の呼び出し側で用意しておき、この関数を呼び出すことにします。nx と ny は行列の寸法 $nx \times ny$ です。

計算時間の計測のため、@assert はコメントアウトしました。
関数は 0 で終わることにしました。w=u+v*alpha で終わってしまうと、関数の戻り値を作るために、余計な計算やメモリ確保が起こり、それが実行時間に含まれる可能性があるからです。

行列 u, v, w を作成する処理も、関数として定義します。

make_uvw.jl

function make_uvw(nx,ny,rng = Random.MersenneTwister(1234))
  u=rand(nx,ny)
  v=rand(Float64, size(u))
  w=similar(u);
  return u,v,w
end

u と v の要素は乱数で満たすことにします。w の中身は未定です。

BenchmarkTools - 実行時間を計測する

BenchmarkTools パッケージを用いて、プログラムの実行時間を計測します。

julia> using Pkg

julia> Pkg.add("BenchmarkTools")

関数の実行に必要なパッケージを読み込んでおきます。

using BenchmarkTools
using Random
using Statistics

早速 ex1_with_matrix の実行時間を計測してみます。

実行時間の計測には、@benchmark マクロを使います。@benchmark マクロの直後に計測したい式を書きます。 setup=() には、計測前に行う準備を書きます。

しばらく、行列の寸法を、nx1=200, ny1=100 とします。@benchmark マクロの中で、 変数 nx1 と ny1 の値を使うため、nx1 と ny1 の前に、$ を付けます。

julia> nx1=200; ny1=100;

julia> rng=Random.MersenneTwister(12345);

julia> # ex1_with_matrix
       @benchmark ex1_with_matrix(u,v,w, $nx1,$ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  312.66 KiB
  allocs estimate:  4
  --------------
  minimum time:     37.794 μs (0.00% GC)
  median time:      51.663 μs (0.00% GC)
  mean time:        66.438 μs (18.64% GC)
  maximum time:     20.115 ms (99.51% GC)
  --------------
  samples:          10000
  evals/sample:     1

まず、BenchmarkTools.Trial: の次の 2行はメモリ確保に関する統計です。memory estimate やalloc estimate: が 0 ではないことで、この計算の実行中に「メモリの確保」が発生したことに注目します。

その後、---- と---- とに囲まれているのが、実行時間の色々な統計値です。
実行時間を互いに比較するための目安として、中央値 median time が、よく用いられます。行列計算の実行時間(の中央値)は 51.663 μs でした。

行列の要素同士の計算

行列の演算の前に @. マクロをつけると、行列の各要素に対する計算を行うことを指示します。

@. w=u+v*alpha

正確には、@. マクロは、配列の要素毎に対する計算を指示する . 演算子を、付けられる演算子や関数の全てに付けることに相当します。この例題では問題ないですが、例えば、行列の積 a*bを含んだ計算に、うっかり @. を適用すると、対応する要素同士の積 a.*b の意味になってしまうので、要注意です (経験者は語る)。

関数として定義します。

ex1_with_dot_matrix.jl

function ex1_with_dot_matrix(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @. w=u+v*alpha
  0
end

実行時間を計測します。

julia> # with_dot_matrix
       @benchmark ex1_with_dot_matrix(u,v,w, $nx1,$ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     10.588 μs (0.00% GC)
  median time:      12.857 μs (0.00% GC)
  mean time:        13.635 μs (0.00% GC)
  maximum time:     503.366 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     4

今度は、メモリ確保は発生しません (allocs estimate: 0) 。

実行時間(の中央値)は、単純な行列計算の　51.663 μs から 12.857 μs へと大幅に (約 1/4 に) 短縮しました。

二重ループによる計算

この例題は、配列の各要素に対する計算としても書けます。

$$\begin{equation*}
w_{i,j} = u_{i,j} + \alpha v_{i,j}
\end{equation*}$$

ここで、$i, j$ は、行列 (2次元配列) の添字であり、全ての要素を巡ります。

この計算は、添字毎に独立しているので、どの順番で計算しても構いません。
添字 i と j を、二重ループで (入れ子の for 文で)回せば、確実に全ての要素を巡ることができます。
この際、内側のループ変数を i にするか、それとも j にするかの、二つの選択があります。

• 第2軸の添字 j を内側で回す二重ループ

配列の要素を a[i,j] と書くとき、最初の添字 i を第1軸 (first axis)の添字、2番目の添字 j を第2軸 (second axis)の添字、といいます

外側のループで第1軸の添字 i を回し、内側のループで第2軸の添字 j を回す書き方です。

for i in 1:nx
  for j in 1:ny
    w[i,j]=u[i,j]+v[i,j]*alpha
  end
end

• 第1軸の添字 i を内側で回す二重ループ

今度は、外側のループで第2軸の添字 j を回し、内側のループで第1軸の添字 i を回す書き方です。

for j in 1:ny
  for i in 1:nx
    w[i,j]=u[i,j]+v[i,j]*alpha
  end
end

それぞれの場合を、関数として定義します。

• 第2軸の添字を内側で回す二重ループ

ex1_double_loop_ij.jl

function ex1_double_loop_ij(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @inbounds for i in 1:nx
    @simd for j in 1:ny
    w[i,j]=u[i,j]+v[i,j]*alpha
    end
  end
  0
end

• 第1軸の添字を内側で回す二重ループ

ex1_double_loop_ji.jl

function ex1_double_loop_ji(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @inbounds for j in 1:ny
    @simd for i in 1:nx
    w[i,j]=u[i,j]+v[i,j]*alpha
    end
  end
  0
end

上に定義した関数では、for 文を高速化するためのマクロを付けました。
- @inbounds を付けると、添字の範囲検査が省略されます。添字が配列の範囲を超えても例外を発生しません。
- @simd を 最も内側の for 文に付けると、CPUが提供する並列計算命令を（可能なら）適用します。

実行時間を計測します。

julia> # 第2軸を内側に
       @benchmark ex1_double_loop_ij(u,v,w, $nx1,$ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     51.452 μs (0.00% GC)
  median time:      63.237 μs (0.00% GC)
  mean time:        66.718 μs (0.00% GC)
  maximum time:     2.000 ms (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     1

julia> # 第1軸を内側に
       @benchmark ex1_double_loop_ji(u,v,w, $nx1,$ny1) setup=(  (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     10.536 μs (0.00% GC)
  median time:      12.498 μs (0.00% GC)
  mean time:        13.228 μs (0.00% GC)
  maximum time:     474.144 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     4

どちらの場合もメモリ確保は起こりませんでした。

実行時間(の中央値)を比較すると、以下のように傾向をまとめられます。
- 第2軸を内側で回した二重ループの実行時間 (63.237 μs) は、行列計算の実行時間 (51.663 μs) よりも長かったです。
- 第1軸を内側で回した二重ループの実行時間 (12.498 μs) は、第2軸を内側で回した二重ループよりも短く (およそ 1/5倍)、行列要素に対する計算の実行時間 (12.857 μs) と同程度でした。

さて、第1軸を内側で回すほうが、第2軸を内側で回すより、速く実行されるのは、冒頭に挙げた Performance tips に解説されている通りです (Julia Documentation, Perfomance Tips > Access arrays in memory order, along columns )

配列の要素は、第1軸が先に回る順番で格納されますから、第1軸の添字を先に増やすと、すぐ隣の配列要素を順で読み書きします。ですので、データの先読みの機能 (キャッシュ)が有効に働く可能性が高くなります。

逆に、第2軸を内側で回すと、飛び飛びに (第1軸の寸法分を増やして)配列要素を読み書きすることになり、キャッシュが失敗する可能性が増えてしまいます。

eachindex で単純ループ

Julia の配列の添字は、連続する整数でも指定できます。「線形の添字 (linear index) 」といいます。

1から配列の長さ (配列全体の数) length(u) まで順番に線形な添字を増やすのは、第1軸を内側で回すのと同じです。

for ij in 1:length(u)
  w[ij]=u[ij]+v[ij]*alpha
end

範囲 1:length(u) で書く代わりに、イテレータ eachindex(u) を使ってスッキリ書けます。

for ij in eachindex(u)
  w[ij]=u[ij]+v[ij]*alpha
end

スッキリ書けただけでなく、実行速度が速くなります (と期待されます)。
軸をまたいで連続した配列の要素が読み書きされるので、キャッシュがさらに有効になりやすくなります。また、繰り返しブロックの最後で実行される繰返しの終了条件の判定が、単純ループにすると少なくなるからです。

@inbounds と @simd のマクロを付けて、関数を定義します。

ex1_eachindex.jl

function ex1_eachindex(u,v,w,  nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @inbounds @simd for ij in eachindex(u)
    w[ij]=u[ij]+v[ij]*alpha
  end
  0
end

実行時間を計測します。

julia> # eachindex
       @benchmark ex1_eachindex(u,v,w, $nx1, $ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     8.945 μs (0.00% GC)
  median time:      10.329 μs (0.00% GC)
  mean time:        10.829 μs (0.00% GC)
  maximum time:     48.689 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     5

eachindex を使った場合の実行時間 (10.329 μs)は、行列要素に対する計算 (12.857 μs) や第1軸を内側で回す二重ループ (12.498 μs) と同程度で、少し短かったです。

CartesianIndices で単純ループ

配列の要素は、CartesianIndex(i,j) を用いても参照できます。CartesianIndex(i,j) は、各軸の添字 i, j を指定します。
すなわち、a[CartesianIndex(i,j)] は a[i,j] と同じ意味です。

関数 CartesianIndices(a) は、配列 a 全体を効率よく回るような CartesianIndex のイテレータを作ります。
eachindex と同じように、第1軸の添字が先に動きます。

ですから、例題は、以下のように書けます。

for ij in CartesianIndices(u)
  w[ij]=u[ij]+v[ij]*alpha
end

計測対象の関数を定義します。

ex1_CartesianIndices.jl

function ex1_CartesianIndices(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @inbounds @simd for ij in CartesianIndices(u)
    w[ij]=u[ij]+v[ij]*alpha
  end
  0
end

実行時間を計測します。

julia> # CartesianIndices
       @benchmark ex1_CartesianIndices(u,v,w, $nx1,$ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     9.372 μs (0.00% GC)
  median time:      11.245 μs (0.00% GC)
  mean time:        11.764 μs (0.00% GC)
  maximum time:     41.984 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     5

CartesianIndicesを使った場合の実行時間 (11.245 μs)は、eachindex による繰返しよりも少し長く、行列要素による計算、第1軸を内側で回す二重ループよりも少し短かったです。

LinearIndices(CartesianIndices()) で単純ループ

関数 LinearIndices(I) は、CartesianIndex のイテレータ I を「線形な添字」のイテレータに変換します。
つまり、以下の書き方は、eachindex(a) を用いた繰返しと同じです。

for ij in LinearIndices(CartesianIndices(u))
  w[ij]=u[ij]+v[ij]*alpha
end

関数を定義します。

ex1_LinearIndices_CartesianIndices.jl

function ex1_LinearIndices_CartesianIndices(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @inbounds @simd for ij in LinearIndices(CartesianIndices(u))
    w[ij]=u[ij]+v[ij]*alpha
  end
  0
end

実行時間を計測します。

julia> # LinearIndices_CartesianIndices
       @benchmark ex1_LinearIndices_CartesianIndices(u,v,w, $nx1, $ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     9.105 μs (0.00% GC)
  median time:      10.437 μs (0.00% GC)
  mean time:        11.001 μs (0.00% GC)
  maximum time:     452.964 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     5

イテレータ LinearIndices(CartesianIndices(...)) を使った場合の実行時間の
中央値は (10.437 μs)は、eachindex による計算と同程度です。

全てを比較してみる。

BenchmarkTools パッケージでは、計測対象を BenchmarkGroup としてまとめておいて、実行時間を一気に計測できます。

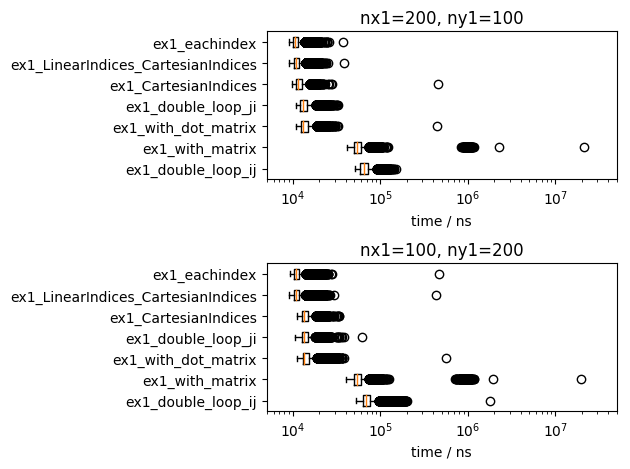
各計測結果には、各計測対象を複数回実行した結果の実行時間の生データが含まれています。これを、boxplot (箱プロット)してみましょう。

行列の寸法が 200x100 の場合、100x200 の場合の二通りについて、グラフで示しました。行列の全体の寸法は変わりませんが、100x200 の方が第1軸の寸法が小さいので、第1軸を内側に回す二重ループが不利になると考えられます。

横軸は、実行時間 (単位 ns) を、対数で表示しました。左ほど実行結果が短いです。実行時間の中央値は、橙色の線で表しました。中央値が短い順に、関数の名前を整列しました。

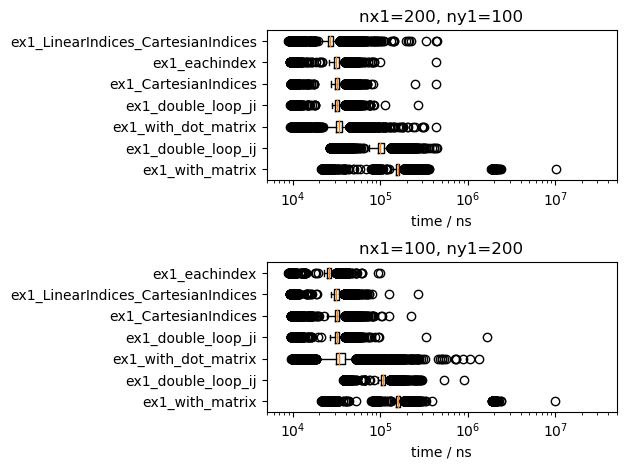
比較として、MacBookProで実行した結果のグラフを示します。この記事の下書きを書くために Jupyter notebook、Google Chrome、Atom エディタを起動していて、それなりに高負荷な環境だと思います。

実行時間の短い方法の順位は、行列の寸法や実行環境で、少し入れ替わっていますが、傾向は変わりません。これまでの説明を復唱しますが、以下のようにまとめられます。

• 単なる「行列の計算」は二重ループより遅く、メモリ確保が発生します。
• 二重ループでは、第1軸を内側で回すほうが速いです
• 単一ループ、すなわち、eachindex(...) と LinearIndices(CartesianIndices(...)) は、第1軸を内側で回すのと同程度に速いです。
• 行列の要素毎の計算も、第1軸を内側で回すのと同程度に速いです。小さいメモリ確保が発生します。

ですので、行列の全ての要素を巡回する場合は、
* 第1軸を内側にした二重ループ
* eachindex(a) を使ったイテレータ
のどちらかで書くのがオススメといえます。

例題2

もう一つの例題は、見かけは、前の例題と同じです。

$$\begin{align*}
w_{i,j} & \leftarrow u_{i+1,j} + \alpha v_{i,j-1}
\end{align*}$$

しかし、添字 i と j は行列全体を巡りません。

• 第1軸の添字 $i$ は、2 から、size(a,1)-1 すなわち、第1軸の寸法から 1 減じた値まで繰返します。
• 第2軸の添字 $j$ は、2 から、size(a,2)-1 すなわち、第2軸の寸法から 1 減じた値まで繰返します。

寸法 4x5 の行列について模式的に書くと、以下のようになります。黒丸 $\bullet$ が読み書きされる要素です。

$$\begin{bmatrix}
\circ & \circ & \circ & \circ & \circ \\
\circ & \bullet & \bullet & \bullet & \circ \\
\circ & \bullet & \bullet & \bullet & \circ \\ \circ & \circ & \circ & \circ & \circ \end{bmatrix} =
%
\begin{bmatrix}
\circ & \circ & \circ & \circ & \circ \\
\circ & \circ & \circ & \circ & \circ \\
\circ & \bullet & \bullet & \bullet & \circ \\
\circ & \bullet & \bullet & \bullet & \circ \end{bmatrix}
+ \alpha
\begin{bmatrix}
\circ & \circ & \circ & \circ & \circ \\
\bullet & \bullet & \bullet & \circ & \circ \\
\bullet & \bullet & \bullet & \circ & \circ \\
\circ & \circ & \circ & \circ & \circ \end{bmatrix}$$

この例題は、離散化した微分方程式を行列方程式として表したときに、時間発展させる場合や、座標変数の境界条件を考慮すべき場合を、模式化したものです。
(この記事は、 @Bimaterial さんの 2次元波動方程式の解の導出と性質 記事への、私のコメント続きも意図しています )。

この計算を行うのには、以下のような方法が考えられます。

• 部分行列の計算
• 部分行列の要素同士の計算
• 二重ループ
• 単純ループ
  • イテレータ CartesianIndices() を使う
  • イテレータ LinearIndices(CartesianIndices())

部分行列の計算

この例題は、行列全体の計算ではなく、添字もズレていますから、単純な行列として書くことはできません。

代わりに、部分配列 (部分行列, サブ行列)を使ってみます。
これは、配列の一部を、部分配列として扱うものです。

例えば、

w_sub=view(w,2:nx-1, 2:ny-1)

とすると、配列 w の部分配列 w_sub が作れます。ここで、部分配列 w_sub は、配列 w において、第1軸の添字が 2 から nx-1 まで、第2軸の添字が 2 から ny-1 までの範囲です。

部分配列は、通常の配列と同じように計算できます。元の配列の複製は作りません。

この例題の核心の部分は、このように書けます。

w_sub=view(w, 2:nx-1, 2:ny-1)
u_sub=view(u, 3:nx,   2:ny-1)
v_sub=view(v, 2:nx-1, 1:ny-2)
w_sub=u_sub+v_sub*alpha

部分配列 u, v, w は、元の配列 u, v, w の異なる部分を指していますが、対応する添字同士で正しく計算されます。

実行時間の計測対象を、関数として定義します。

ex2_view.jl

function ex2_view(u,v,w, nx=size(u,1),ny=size(u,2), alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  w_sub=view(w,2:nx-1, 2:ny-1)
  v_sub=view(v, 2:nx-1, 1:ny-2)
  u_sub=view(u, 3:nx, 2:ny-1)
  w_sub=u_sub+v_sub*alpha
  0
end

例題1と同様に、しばらく、行列の寸法を、nx1=200, ny1=100 とします。
実行時間を計測します。

julia> nx1=200; ny1=100;

julia> # CartesianIndices
       @benchmark ex2_view(u,v,w, $nx1, $ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  303.53 KiB
  allocs estimate:  6
  --------------
  minimum time:     42.012 μs (0.00% GC)
  median time:      52.443 μs (0.00% GC)
  mean time:        103.169 μs (46.16% GC)
  maximum time:     112.921 ms (99.88% GC)
  --------------
  samples:          10000
  evals/sample:     1

例題1の行列計算と同様に、メモリ確保が発生してしました。
実行時間(の中央値)は 52.443 μs でした。例1の行列全体の計算 (51.663 μs) と同程度でした。

部分行列の要素同士の計算

部分配列の計算に @. を前につけると、部分配列の各要素の計算となります。

@. w_sub=u_sub+v_sub*alpha

関数を定義します。

ex2_dot_view.jl

function ex2_dot_view(u,v,w, nx=size(u,1),ny=size(u,2), alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  w_sub=view(w,2:nx-1, 2:ny-1)
  v_sub=view(v, 2:nx-1, 1:ny-2)
  u_sub=view(u, 3:nx, 2:ny-1)
  @. w_sub=u_sub+v_sub*alpha
  0
end

実行時間を計測します。

julia> # dot_view
　　　　@benchmark ex2_dot_view(u,v,w, $nx1, $ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  192 bytes
  allocs estimate:  3
  --------------
  minimum time:     12.832 μs (0.00% GC)
  median time:      15.110 μs (0.00% GC)
  mean time:        16.108 μs (0.00% GC)
  maximum time:     38.263 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     3

例1の行列の全要素に対する計算では発生していなかった「メモリ確保」が、ほんの少し発生しました。
実行時間(の中央値)を比較すると、52.443 μs から 15.110 μs へと大幅に (約 1/3 に) 短縮しました。

二重ループによる計算

この例は、添字を使った二重ループで自然に書くことができます。

第2軸を内側で回す二重ループを関数として用意します。

ex2_double_loop_ij.jl

function ex2_double_loop_ij(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @inbounds for i in 2:nx-1
    @simd for j in 2:ny-1
      w[i,j]=u[i+1,j]+v[i,j-1]*alpha
    end
  end
  0
end

今度は、第1軸を内側で回す二重ループを関数として定義します。

ex2_double_loop_ji.jl

function ex2_double_loop_ji(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @inbounds for j in 2:ny-1
    @simd for i in 2:nx-1
      w[i,j]=u[i+1,j]+v[i,j-1]*alpha
    end
  end
  0
end

実行時間を計測します。

julia> # 第2軸を内側に
       @benchmark ex2_double_loop_ij(u,v,w, $nx1,$ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     54.765 μs (0.00% GC)
  median time:      75.025 μs (0.00% GC)
  mean time:        78.491 μs (0.00% GC)
  maximum time:     949.207 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     1

julia> # 第1軸を内側に
       @benchmark ex2_double_loop_ji(u,v,w, $nx1,$ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     10.918 μs (0.00% GC)
  median time:      13.104 μs (0.00% GC)
  mean time:        13.779 μs (0.00% GC)
  maximum time:     32.241 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     4

実行時間(の中央値)を比較すると、以下のようになります。
- 第2軸を内側で回した二重ループの実行時間 (75.025 μs) は、部分配列(部分行列)の実行時間 (52.443 μs) よりも長かったです。
- 第1軸を内側で回した二重ループの実行時間 (13.104 μs) は、第2軸を内側で回した二重ループよりも短く (およそ 1/5倍)、部分配列行列の要素の実行時間 (15.110 μs) と同程度で、少し短かったです。

CartesianIndices で単純ループ

例2では、添字は行列全体を巡るわけではないので eachindex(a) は使えません。
イテレータ CartesianIndices は、配列の一部を切り出すこともできます。
すなわち、 CartesianIndices((2:nx-1,2:ny-1)) は、

• 第1軸を 1から nx-1 まで、
• 第2軸を 1から ny-1 まで

巡回する CartesianIndex のイテレータです。第1軸の方が内側で回ります。

CartesianIndex(i,j) を関数 Tuple に適用すると、各軸の添字が得られます。
すなわち、計算の主な部分は、以下のように書けます。

for ij in CartesianIndices((2:nx-1,2:ny-1))
  i,j=Tuple(ij)
  w[i,j]=u[i+1,j]+v[i,j-1]*alpha
end

関数として定義します。

ex2_CartesianIndices.jl

function ex2_CartesianIndices(u,v,w, nx=size(u,1),ny=size(u,2),alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  @inbounds @simd for ij in CartesianIndices((2:nx-1,2:ny-1))
    i,j=Tuple(ij)
    w[i,j]=u[i+1,j]+v[i,j-1]*alpha
  end
  0
end

実行時間を計測します。

julia> # CartesianIndices
       @benchmark ex2_CartesianIndices(u,v,w, $nx1,$ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     11.389 μs (0.00% GC)
  median time:      13.550 μs (0.00% GC)
  mean time:        14.200 μs (0.00% GC)
  maximum time:     33.031 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     4

CartesianIndicesを使った場合の実行時間の中央値 (13.550 μs)は、
部分配列の要素に対する計算や第1軸を内側で回す二重ループと同程度で、少し短かったです。

LinearIndices(CartesianIndices()) で単純ループ

CartesianIndices() を LinearIndices に適用すると、「線形な添字」が得られます。

u, v, w に対する線形な添字はズレていますから、各々の行列の要素を指定するイテレータを用意してしましょう。これは、同じ添字で取り出せます。
すなわち、核心の部分は、以下のように書けます。
ここで、
- w_I は w に対する添字のイテレータ
- u_J は u に対する添字のイテレータ
- v_K は v に対する添字のイテレータ
です。

w_I=LinearIndices(CartesianIndices( (2:nx-1, 2:ny-1)))
u_J=LinearIndices(CartesianIndices( (3:nx,   2:ny-1)))
v_K=LinearIndices(CartesianIndices( (2:nx-1, 1:ny-2)))

for m in 1:length(w_I)
  i=w_I[m]
  j=u_J[m]
  k=v_K[m]
  w[i]=u[j]+v[k]*alpha
end

関数として定義します。

ex2_LinearIndices_CartesianIndices.jl

function ex2_LinearIndices_CartesianIndices(u,v,w, nx=size(u,1),ny=size(u,2), alpha=0.3)
  # @assert size(u)==(nx,ny)
  # @assert size(v)==(nx,ny)
  # @assert size(w)==(nx,ny)
  w_I=LinearIndices(CartesianIndices( (2:nx-1, 2:ny-1)))
  u_J=LinearIndices(CartesianIndices( (3:nx, 2:ny-1)))
  v_K=LinearIndices(CartesianIndices( (2:nx-1, 1:ny-2)))
  @inbounds @simd for m in 1:length(w_I)
    i=w_I[m]
    j=u_J[m]
    k=v_K[m]
    w[i]=u[j]+v[k]*alpha
  end
  0
end

実行時間を計測します。

julia> # LinearIndices_CartesianIndices
       @benchmark ex2_LinearIndices_CartesianIndices(u,v,w, $nx1, $ny1) setup=( (u,v,w)=make_uvw($nx1,$ny1, $rng))
BenchmarkTools.Trial:
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     8.906 μs (0.00% GC)
  median time:      10.400 μs (0.00% GC)
  mean time:        10.895 μs (0.00% GC)
  maximum time:     47.163 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     5

LinearIndices(CartesianIndices(...))を使った場合の実行時間 (10.400 μs)は、CartesianIndices(...)を使った場合の実行時間 (13.550 μs) と同程度で、少し短かったです。

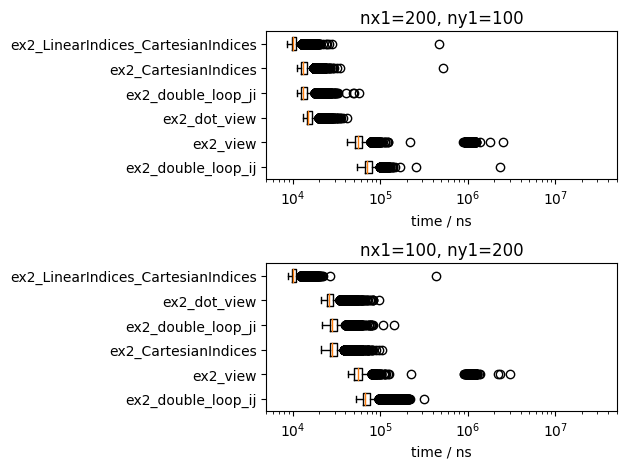
全てを比較してみる

例題1 と同じように、例題2の全ての計測対象を比較してみましょう。

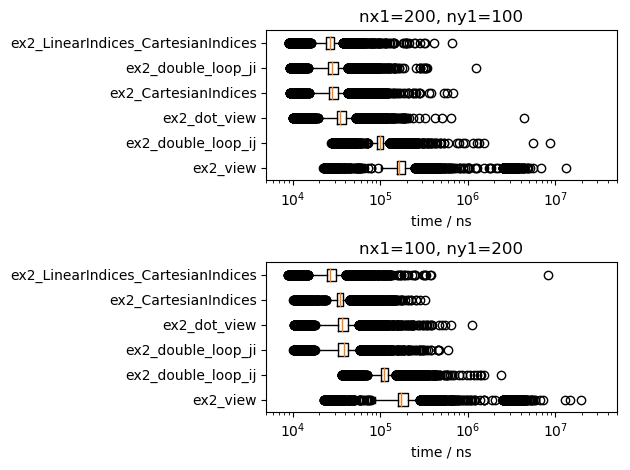
比較として、MacBookProで実行した結果のグラフを示します。

実行時間の短い方法の順位は、行列の寸法や実行環境で、少し入れ替わっています。が、傾向は変わっていません。以下のようにまとめられます。

• 単なる「部分行列の計算」は、二重ループより遅く、メモリ確保が発生します。
• 二重ループでは、第1軸を内側で回すほうが速いです。
• 部分行列の要素毎の計算も、第1軸を内側で回すのと同程度に速いです。小さいメモリ確保が発生します。
• 単一ループ、すなわち、LinearIndices(CartesianIndices(..)) は、第1軸を内側で回すのと同程度に速いです。

ですので、行列の全ての要素を巡回する場合は、まず

• 第1軸を内側にした二重ループ

で書いておいて、計測しながら、LinearIndices(CartesianIndices()) に書き換えるのがオススメといえます。