はじめに
Julia Advent Calendar 2018 の 12日目です。
Julia Advent Calendar 2015 では、Julia言語で、単位付き数値の算術を支援する Physical.jl パッケージを紹介しました。 → 「 Juliaで、単位付き数値の算術 - Physical.jl パッケージ 」 (以後、前記事と書きます)。しかし、このパッケージは、もうメンテナンスされていませんし、Julia 1.0 では動作しません。
本記事では、Julia 1.0 向けに同等以上の機能を提供する Unitful パッケージを紹介します。
インストール
Julia 1.0 で導入された新しいパッケージ・マネージャで導入できます。
Julia の REPLで、] キーを入れると、パッケージ・マネージャが起動します。
(v1.0) pkg> add Unitful
パッケージ・マネージャを抜けるには CTRL+C キーを押します。
簡単な例から
Unitful パッケージを読み込みます。
julia> using Unitful
単位は、ダブル・クォート文字列の前に、英小文字 u を付けて記します。
小文字の m は、長さの単位「メートル」を表します。単位の m の前に、SI単位系の接頭辞 (G, M, d, k, m, μ, n, p など)を一つだけ付けることができます。
julia> u"m"
m
julia> u"mm"
mm
julia> u"μm"
μm
上の最後の例で、$10^{-6}$ を意味する接頭辞 μ は、ギリシャ文字のミューです。Julia の REPLで、バックスラッシュ \ mu と打鍵してから TABキーを押すと μ に変換されます。このような Unicode 文字の TAB補完入力についても以前紹介しました。 → [Julia] UTF-8 表記の演算子たち > Unicode の TAB入力補完
小文字の s は、時間の単位「秒」です。
小文字の g は、質量の単位「グラム」です。
これらにも、接頭辞をつけることができます。
julia> u"s"
s
julia> u"μs"
μs
julia> u"g"
g
julia> u"kg"
kg
数字の直後に単位を書いたものが「量」です。
数字の直後に単位がないと(例えば空白が入っていると)、例外が発生します。
数に、後から単位を付けるには、単位を乗じるとよいでしょう。
julia> 1u"m"
1 m
julia> 1 u"m"
ERROR: syntax: extra token "u" after end of expression
julia> 1 * u"m"
1 m
比較演算子 == や近似比較関数 isapprox を用いて、量同士を比較できます。
単位は異なっても同じ量であれば真 true と判定されます。
異なる量であれば偽 false と判定されます。
julia> 1.0u"m" == 1000.0u"mm"
1.0 m
julia> 1.0u"m" == 1000.0u"mm"
true
julia> 0.9u"m" == 1000.0u"mm"
false
julia> isapprox(1.0u"m", 1000.00001u"mm")
true
比較演算子 == で、単位を比較できます。
単位は完全に一致するときに限り、真 true です。次元が等しくても接頭辞が異なれば、偽 false です。
julia> u"m" == u"m"
true
julia> u"m" == u"mm"
false
次元が異なる量を比較した場合も 偽 false になります ( Physical.jl では例外を発生していました)。
julia> u"m" == u"s"
false
「量」と「単位」を比較しても 偽 false になります。
julia> u"m" == 1u"m"
false
量の加減算
同じ次元の量は、加減算できます。
同じ次元で接頭辞が異なる単位を持つ量を加減算すると、2つ目以降の量の単位が、最初の量の単位に変換されます。
julia> 1.0u"m" + 0.1u"m"
1.1 m
julia> 1.0u"m" + 0.001u"m"
1.001 m
julia> 1.0u"m" + 1.0u"mm"
1.001 m
julia> 1.0u"m" + 1.0u"cm" + 1.0u"mm"
1.011 m
次元が異なる量を加減算すると、例外が発生します。
julia> 1u"m" + 1u"s"
ERROR: DimensionError: 1 m and 1 s are not dimensionally compatible.
Stacktrace:
[1] +(::Quantity{Int64,𝐋,Unitful.FreeUnits{(m,),𝐋,nothing}}, ::Quantity{Int64,𝐓,Unitful.FreeUnits{(s,),𝐓,nothing}}) at /Users/hs/.julia/packages/Unitful/b6IPw/src/quantities.jl:87
[2] top-level scope at none:0
単位や量の乗除
単位同士を乗除すると、単位も乗除されます。同じ単位の冪(べき)乗も計算されます。
julia> u"m" / u"s"
m s^-1
julia> 1u"m^3" / 1u"m"
1.0 m^2
量を単位で乗除したり、量同士を乗除できます。単位は一つにまとめられます。
julia> 1u"m" / u"s"
1 m s^-1
julia> 1u"m" / 1u"s"
1.0 m s^-1
同じ単位同士で割って単位が相殺すると、数 ( Float64, Int64, Complex{Float64} などの型) になります。
julia> 1u"m" / 1u"m"
1.0
しかし、量を、同じ次元の接頭辞が異なる単位や量で割っても、単位は相殺せず残ります。単位を消して数にするには、単位 NoUnits に変換します。
julia> (1u"m" / 1u"mm")
1.0 m mm^-1
julia> 1u"mm" / 1u"m" |> NoUnits
1000.0
次元
関数 dimension(x) は、単位x の次元を返します。量 x を引数にすると、x の単位の次元を返します。
𝐋, 𝐌, 𝐓 は、それぞれ長さ、質量、時間の次元です。
julia> dimension(u"g")
𝐌
julia> dimension(u"m")
𝐋
julia> dimension(u"s")
𝐓
julia> dimension( 1u"J" )
𝐋^2 𝐌 𝐓^-2
上で紹介したように、単位の比較は、完全一致を判定します。
次元の一致を判定するには、それぞれを次元に判定してから、比較します。
julia> dimension( 1u"m" ) == dimension( 1u"mm" )
true
julia> dimension( 1u"m" ) == dimension( 1u"s" )
false
julia> dimension( 1u"m" ) == dimension( 1u"inch" )
true
julia> dimension( u"Pa" ) == dimension( u"dyn/cm^2")
true
数を取り出す
量の数字部分を取り出すには ustrip 関数を使います。
julia> ustrip( 1.2u"m" )
1.2
単位を取り出す
量の単位を取り出すには unit 関数を使います。
julia> unit( 1u"mm" )
mm
julia> typeof(ans)
Unitful.FreeUnits{(mm,),𝐋,nothing}
julia> typeof( dimension( 1u"mm"))
Unitful.Dimensions{(Unitful.Dimension{:Length}(1//1),)}
関数 unitで返される単位や、関数 dimensionで返される次元は、FreeUnits 、Dimensions, Dimension などの型であり、文字列ではありません。
量、単位、次元の文字列が欲しい場合には、関数 sprintf と関数showを組み合わせるとよいでしょう。
julia> sprint( show, 1u"m/s^2" )
"1 m s^-2"
julia> sprint( show, u"m/s^2" )
"m s^-2"
julia> sprint( show, dimension(u"m/s^2") )
"𝐋 𝐓^-2"
単位の変換
ある量の単位を、同じ次元の別の単位に変換するには、関数 uconvert(u, x) を用います。第二引数 x の単位や量を、第一引数u の単位に変換します。
既に使っていますが、中置き形式の演算子 |> を用いることもできます。すなわち、 |> の左に単位や量 x を、右に単位 u をおくと、uconvert(u,x) を呼び出したのと同じになります (対話形式で計算するのに、便利な記法です)。
julia> uconvert( u"mm", 1u"m")
1000//1 mm
julia> 1u"m" |> u"mm"
1000//1 mm
julia> float(ans)
1000.0 mm
julia> 1u"Pa" |> u"N" / u"m^2"
1//1 N m^-2
julia> float(ans)
1.0 N m^-2
関数 uconvert で単位が変換できない場合には、例外が発生します。
julia> 1u"m" |> u"s"
ERROR: DimensionError: s and m are not dimensionally compatible.
SI 単位系
SI単位系が定義されています。
すでに説明した長さ、質量(重さ)、時間に加えて、電流、温度、物質量、光度の基本単位が定義されています。
julia> u"A"
A
julia> u"K"
K
julia> u"mol"
mol
julia> u"cd"
cd
更に、SI単位系の主要な組立単位も定義されています。これらにも、SI単位系の接頭辞をつけることができます。
julia> u"N"
N
julia> u"J"
J
julia> u"Pa"
Pa
julia> u"C"
C
julia> u"V"
V
julia> u"F"
F
julia> u"H"
H
エネルギーの単位
J (joule, ジュール)はエネルギーの単位です。 J に等価な組立単位が複数あります。
julia> 1u"kg" * (1u"m/s")^2 |> u"J"
1//1 J
julia> 1u"C" * 1u"V" |> u"J"
1//1 J
julia> 1u"A/m" * u"T"|> u"J/m^3"
1//1 J m^-3
最初の例は運動エネルギー、2つ目の例は、コンデンサに蓄積されたエネルギーです。
3つ目の例は、磁性体の $BH$ 積がエネルギーの体積密度に相当することを表しています。
定義済の定数
Unitful パッケージの pkgdefaults.jl ファイルに、たくさんの単位や定数が定義されています。
長さや圧力
julia> # 重力加速度
1u"gn"
9.80665 m s^-2
julia> # インチ
1u"inch"
1 inch
julia> 1u"inch" |> u"mm"
127//5 mm
julia> # 小数で表す
float(ans)
25.4 mm
julia> # 気圧
1u"atm" |> u"hPa"
4053//4 hPa
julia> # pounds per square inch
1u"psi"
1 psi
julia> ans |> u"Pa"
6894.757293168361 Pa
julia> 1u"atm" |> u"psi"
14.695948775513449 psi
cgs単位
julia> dimension( u"dyn") == dimension( u"N" )
true
julia> 1.0u"dyn" |> u"N"
1.0e-5 N
julia> dimension( u"erg") == dimension( u"J" )
true
julia> 1.0u"erg" |> u"J"
1.0e-7 J
電磁気学
julia> # 素電荷 (1つの電子の電荷)
1u"q"
1.6021766208e-19 C
julia> # 電子ボルト
u"eV"
eV
julia> 1u"eV" |> u"J"
1.6021766208e-19 J
$\sqrt{\dfrac{1}{\epsilon_0\mu_0}}=c$
ϵ は \ epsilon で TAB補完入力できます。 → [Julia] UTF-8 表記の演算子たち > Unicode の TAB入力補完
julia> # 光速
1.0u"c" |> u"m/s"
2.99792458e8 m s^-1
julia> # 真空の透磁率
1u"μ0"
1.2566370614359173e-6 H m^-1
julia> # 真空の誘電率。
1u"ϵ0"
795774.7154594767 m H^-1 c^-2
julia> ( 1u"ϵ0" * 1u"μ0" )^(-1//2)
1.0 c
量子力学
波長 $\lambda$ の単色光の光子(フォトン)エネルギーは $\dfrac{hc}{\lambda}$ です。
julia> # プランク定数
1u"h"
6.62607004e-34 J s
julia> # hc を計算しておく。エネルギーは電子ボルト(eV)、波長は nm で表示する
hc=1u"h" * 1u"c" |> u"eV*nm"
1239.841973964072 nm eV
julia> # 波長 550nm 緑色単色光のフォトンエネルギー
hv= hc/ 550u"nm"
2.2542581344801307 eV
julia> # 1 mW パワーの単色光の光子束 (1s当たりの光子数)
1u"mW" / hv |> u"s^-1"
2.768764158112999e15 s^-1
$\dfrac{\hbar^2}{2m_e}\left(\dfrac{\pi}{a}\right)^2$
ħ は \hbar で、TAB補完入力できます。
julia> # 電子の静止質量
1u"me"
9.10938356e-31 kg
julia> # Planck定数 を 2pi で割った値
1u"ħ"
1.0545718001391127e-34 J s
julia> 1u"ħ" |> u"eV*s"
6.582119514467407e-16 s eV
julia> 1u"ħ"^2 / (2u"me") *(pi / 1u"nm")^2 |> u"eV"
0.37603015907078846 eV
新しい単位を定義する
定義済の単位や量を使って、新しい単位を定義するには、関数 @unit を使います。
ただし、新しい単位を定義しただけでは u"単位" の形式では用いることはできません。u"単位" の形式では用いることができるように「登録」する必要があります。
REPLで作業している場合には Main モジュールに新しい単位が定義されるので、予め Unitful.register(Main) を実行しておきます。
関数 @unit は、5つの引数を取ります。
第一引数は、新しい単位のシンボル、第二引数は、新しい単位の文字列、第三引数は、新しい単位に対応する型の名前(の一部)になります。
第四引数は、定義済みの単位や量による新しい単位の定義です。
最後の第五引数は、SI単位系の接頭辞を使うか否かを指定します。
前記事にならい、尺 (しゃく)、閒 (けん)、坪 (つぼ) の単位を作ってみましょう。
julia> Unitful.register(Main);
julia> @unit 尺 "尺" Shaku (10//33)u"m" false
尺
julia> @unit 閒 "閒" KenJP 6u"尺" false
閒
julia> @unit 坪 "坪" Tsubo (1u"閒")^2 false
坪
julia> 30u"坪" |> u"m^2"
12000//121 m^2
julia> float(ans)
99.17355371900827 m^2
30坪は、100平米弱ですね。
モジュール内で、新しい単位を定義する方法は少し面倒なので、割愛します。
Unitful のドキュメントや、Unitful を元にしたパッケージのソースを読むことを勧めます。
範囲や配列に単位をつける
範囲 (Range)や配列に、単位をつけることができます。
型を調べると、量を要素とするRangeや、量を要素とする配列になっています。
julia> LinRange(0,2,50)*u"s"
50-element LinRange{Quantity{Float64,𝐓,Unitful.FreeUnits{(s,),𝐓,nothing}}}:
0.0 s,0.0408163 s,0.0816327 s,…,1.87755 s,1.91837 s,1.95918 s,2.0 s
julia> rand(3)*u"s"
3-element Array{Quantity{Float64,𝐓,Unitful.FreeUnits{(s,),𝐓,nothing}},1}:
0.7882976213775315 s
0.8501422312233349 s
0.4281156627121119 s
単位を変換するには .|> を、数を取り出すには、ustrip.() を使います。ピリオド . を忘れないように。
Range型
julia> LinRange(0,2,50)*u"s" .|> u"ms"
50-element Array{Quantity{Float64,𝐓,Unitful.FreeUnits{(ms,),𝐓,nothing}},1}:
0.0 ms
40.816326530612244 ms
81.63265306122449 ms
122.44897959183673 ms
163.26530612244898 ms
204.08163265306123 ms
244.89795918367346 ms
285.7142857142857 ms
326.53061224489795 ms
367.34693877551024 ms
⋮
1673.4693877551022 ms
1714.2857142857142 ms
1755.1020408163265 ms
1795.9183673469388 ms
1836.734693877551 ms
1877.5510204081634 ms
1918.3673469387754 ms
1959.1836734693877 ms
2000.0 ms
julia> ustrip.( ans )
50-element Array{Float64,1}:
] 0.0
40.816326530612244
81.63265306122449
122.44897959183673
163.26530612244898
204.08163265306123
244.89795918367346
285.7142857142857
326.53061224489795
367.34693877551024
⋮
1673.4693877551022
1714.2857142857142
1755.1020408163265
1795.9183673469388
1836.734693877551
1877.5510204081634
1918.3673469387754
1959.1836734693877
2000.0
Array型
julia> rand(3)*u"s" .|> u"ms"
3-element Array{Quantity{Float64,𝐓,Unitful.FreeUnits{(ms,),𝐓,nothing}},1}:
306.0519390349252 ms
774.9537090727616 ms
229.87662378240236 ms
julia> ustrip.( ans )
3-element Array{Float64,1}:
306.0519390349252
774.9537090727616
229.87662378240236
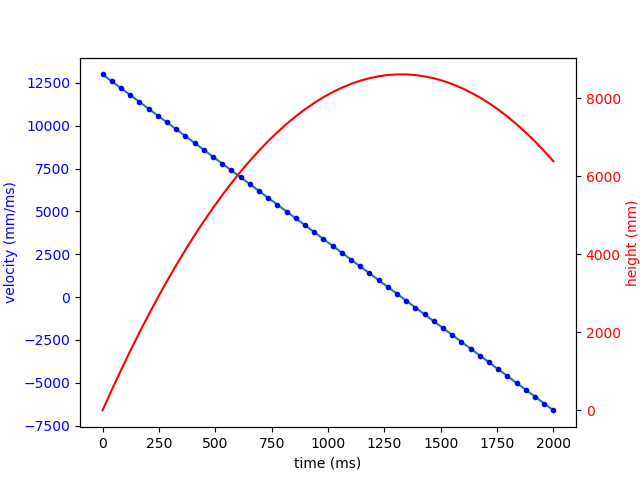
鉛直上向きに投げた球の速度と高さ
鉛直上向きに投げた球の速度と高さのグラフを描く例を、前の記事で紹介しました。 → 単位付き数値ベクトルの計算
同じことを Unitful で書いてみます。量を要素とする Range型が活躍します。
using Unitful
v0= 13u"m/s"
ts= LinRange(0,2,50)*u"s"
vs= v0 .- 1u"gn" *ts
ys=v0*ts .- 1u"gn" *ts.^2/2
ts= ts .|> u"ms"
vs= vs .|> u"mm/s"
ys= ys .|> u"mm"
長さは mm 単位で、時間は ms単位で表示してみます。
using PyPlot
plot( ustrip.(ts), ustrip.(vs), label="velocity")
using PyPlot
plot( ustrip.(ts) , ustrip.(vs), "b.")
ax1 = gca()
ax1[:set_xlabel]("time (ms)")
ax1[:set_ylabel]("velocity (mm/ms)", color="b")
for t1 in ax1[:get_yticklabels]()
t1[:set_color]("b")
end
ax2 = ax1[:twinx]()
ax2[:plot]( ustrip.(ts), ustrip.(ys), "r-")
ax2[:set_ylabel]("height (mm)", color="r")
for tl in ax2[:get_yticklabels]()
tl[:set_color]("r")
end
Gauss単位系を、少し体験する
SI単位系では電磁気の量を表すために、次元を一つ (電流) 用意しています。
これに対して、電磁気量の次元を用意せず、長さ、質量、時間の次元のみで表す単位系があります。複数の表記がありますが、Gauss単位系がよく整備されています。
電磁気学・高エネルギー・物性の文献では、Gauss単位系で書かれたものが多くあります。SI単位系との換算は慣れないと難しいと思います。
Unitful パッケージを用いて、Gauss単位とSI単位系との対応を少しだけ体験してみます。なお、Gauss単位系では、長さ、質量、時間を cm, g, s で表します (cgs単位系)。
電荷
まず、電荷の単位に着目します。
二つの点電荷 $Q_1, Q_2$ に働く力 $f$ を表すクーロン Coulomb の法則から出発します。
SI単位系のクーロンの法則は
$$f = \dfrac{1}{4\pi\epsilon_0}\dfrac{Q_1Q_2}{r^2}$$
です。上式から、電荷 $Q$ の次元を求めると、$[\mathrm{C}] = [\mathrm{A}] \cdot[\mathrm{s}]$ を確認できます。
julia> dimension( sqrt(1u"N"*1u"ϵ0"*1u"m"^2) )
𝐈 𝐓
julia> 1u"A" * 1u"s" |> u"C"
1//1 C
これに対して、Gauss単位系のクーロンの法則は
$$f = \dfrac{Q_1Q_2}{r^2}$$
です。この式から、電荷 $Q$の次元を求めると、
julia> sqrt(1u"dyn"*1u"m"^2)
1.0 dyn^1/2 m
julia> dimension( sqrt(1u"dyn"*1u"m"^2) )
𝐋^3/2 𝐌^1/2 𝐓^-1
すなわち、Gauss単位系の電荷の単位は、以下のように決めます。
$$[\mathrm{dyn}^{\frac{1}{2}}\cdot\mathrm{s}] = [\mathrm{g}^{\frac{1}{2}}\mathrm{cm}^{\frac{3}{2}}\mathrm{s}^{-1}]$$
これを、C_gs という単位で定義しましょう。
julia> C_gs=1u"cm^(3//2)*g^(1//2)*s^(-1)"
1g^1/2 cm^3/2 s^-1
julia> dimension(C_gs)
𝐋^3/2 𝐌^1/2 𝐓^-1
SI単位系の $1~\mathrm{C}$ に相当する、Gauss単位系の電荷 $Q_{gs}$ を求めてみます。
$Q_1=Q_2=1~\mathrm{C}, r=1~\mathrm{m}$ として、同じ力を、二つの単位系で表記します。
$$f = \dfrac{1}{4\pi\epsilon_0}\dfrac{\left(1~\mathrm{C}\right)^{2}}{\left(1~\mathrm{m}\right)^{2}}= \dfrac{\left(Q_{gs}\right)^{2}}{\left(1~\mathrm{m}\right)^{2}}$$
$Q_{gs}$ を解いてみます。 m と cm との換算などは、Unitful に任せます。
julia> # 力
f=1/(4pi*u"ϵ0")*(1u"C")^2/(1u"m")^2 |> u"dyn"
8.987551787368176e14 dyn
julia> # Q_gs を求める
Q_gs=sqrt( f * (1u"m")^2 )
0.00031622776601683794 C H^1/2 c m^-1/2
julia> # 「変換係数」
Q_gs / C_gs |> NoUnits
2.99792458e9
julia> c0=ustrip( 1u"c" |> u"cm/s" )
29979245800//1
julia> c0 / 10.
2.99792458e9
最後の一つ前に定義した変数 c0 は、光速を cm/s単位で表した量の数の部分で、$\{c\}$ と書かれることがあります。
最後の結果は、SI単位系の $1~\mathrm{C}$ と、Gauss単位系の$1~\mathrm{C_{\mathrm{gs}}}$ との対応を表します。
$$1~\mathrm{C} = \dfrac{\{c\}}{10}~\mathrm{C}_{\mathrm{gs}}$$
電流
次に、電流の単位に着目します。
十分に長い平行に置かれた2本の線に電流が流れているときに働く、単位長当たりの力 (Ampere 力)は、SI単位系では、以下のように表されます。
$$ f = \dfrac{2\mu_0}{4\pi}\dfrac{I_1I_2}{r} $$
上式から電流の次元が確かに得られます。
julia> dimension( sqrt( 1u"N/m" / (2u"μ0"/u"m") ))
𝐈
Gauss単位系での Ampere力は、以下のように表されます。
$$ f = \dfrac{2}{c^2}\dfrac{I_1I_2}{r} $$
電流の次元を求めてみると、
julia> dimension( sqrt( 1u"dyn/cm" * u"c"^2 * u"cm" ) )
𝐋^3/2 𝐌^1/2 𝐓^-2
Gauss単位系の電流の単位は、以下のようになります。
$$[\mathrm{dyn}^{\frac{1}{2}}\cdot\mathrm{cm}\cdot\mathrm{s}^{-1}] = [\mathrm{g}^{\frac{1}{2}}\mathrm{cm}^{\frac{3}{2}}\mathrm{s}^{-2}]$$
これを、A_gs という単位で定義しましょう。
julia> A_gs=1u"cm^(3//2)*g^(1//2)*s^(-2)"
1 g^1/2 cm^3/2 s^-2
SI単位系の $1~\mathrm{A}$ に相当する、Gauss単位系の電流 $I_{gs}$ を求めてみます。
$I_1 = I_2 = 1~\mathrm{A}, r=1~\mathrm{m}$, 線の長さを $l = 1~\mathrm{m}$ として、線に働く力を、二つの単位系で表記します。
$$ f l = \dfrac{2\mu_0}{4\pi}\dfrac{\left(1~\mathrm{A}\right)^2}{1~\mathrm{m}} \times 1~\mathrm{m} = \dfrac{2}{c^2}\dfrac{I_{gs}^2}{1~\mathrm{m}} \times 1~\mathrm{m} $$
$I_{gs}$ を解くと
julia> fl=2u"μ0"/(4pi)*(1u"A")^2*1u"m"/1u"m" |> u"N"
2.0000000000000002e-7 N
julia> I_gs=sqrt(fl*(1u"c")^2*1u"m"/1u"m"/2)
0.00031622776601683794 N^1/2 c
julia> I_gs / A_gs |> NoUnits
2.99792458e9
電荷と同じ「変換係数」が、電流でも得られます。
$$1~\mathrm{A} = \dfrac{\{c\}}{10}~\mathrm{A}_{\mathrm{gs}}$$
実は、電流は電荷の時間変化ですが、二つの単位系で同じ式 (連続の式)
$$I + \dfrac{dQ}{dt} = 0 $$
で表されることにあることに着目すると、電流の次元を電荷の次元から直ちに導いたり、電荷と電流の「変換係数」が等しいことも、すぐに分かるのでした。
静電ポテンシャル
今度は、静電ポテンシャルの単位です。電荷 $q$ に静電ポテンシャル $\Phi$ を乗じたものが静電エネルギー $U=q\Phi$ です。この式は、SI単位系とGauss単位系で共通ですが、電荷の次元か異なるので、静電ポテンシャルの次元も異なります。
julia> # SI単位系の静電ポテンシャルの次元
dimension( u"V" )
𝐋^2 𝐌 𝐈^-1 𝐓^-3
julia> # cgs単位系の静電ポテンシャルの次元
dimension( 1u"erg" / C_gs )
𝐋^1/2 𝐌^1/2 𝐓^-1
Gauss単位系の静電ポテンシャルの単位 V_gs を、以下のように決めます。
julia> V_gs=1u"g^(1//2)*cm^(1//2)*s^(-1)"
1 g^1/2 cm^1/2 s^-1
julia> 1u"J" / Q_gs / V_gs |> NoUnits
0.00333564095198152
julia> 1e8/c0
0.0033356409519815205
$$1~\mathrm{V} = \dfrac{10^{8}}{\{c\}}~\mathrm{V}_{\mathrm{gs}}$$
電気抵抗など
Gauss単位系で、電磁気量の次元が、力学量の次元と一致してしまうことがあります。
例えば、電気抵抗 $R$ の単位は、オームの法則 $V = RI$ から決まります。
電気抵抗の逆数は、コンダクタンス $G = 1/R$ です。 オームの法則は $I=GV$ となります。
julia> # 電気抵抗の単位
V_gs / A_gs
1.0 s cm^-1
julia> # コンダクタンスの単位
A_gs / V_gs
1.0 cm s^-1
電気抵抗の単位は「速度」の単位の逆数となり、コンダクタンスの単位は「速度」の単位と一致してしまいました。
別の例として、電気容量 $C$ の単位は、コンデンサに蓄積される電荷 $Q = CV$ から決まります。
julia> # 電気容量の単位
C_gs / V_gs
1.0 cm
「長さ」の単位と一致してしまいました。
すなわち、Gauss単位系では、単位や次元から物理量を区別することができないのです。どの物理量に着目しているかは、使う人なら分かっているね、という立場ですね。
終わりに
以上、Unitful パッケージを使って、単位付き数字を扱う例を駆け足で紹介しました。
dBなどの対数表示の単位や、セ氏温度 (°C)・華氏温度(°F) の単位と変換もできるそうですが、試していませんので割愛しました。