Juliaで、単位付き数値の算術 - Physical.jl パッケージ

[2018/01/19 コメント] 3年前の記事に「いいね」を頂きましたので最新事情を手短かに補足します。
Physical.jlパッケージはJulia 0.6以降動作しません。同様の機能を持つものとして Unitful.jl パッケージが公開されています。http://ajkeller34.github.io/Unitful.jl/stable/
Physical.jlと似た感じで利用できます。

[2018/12/12] Unitfulパッケージの紹介記事を書きました。→ Julia 1.0で単位付き数値の算術 - Unitful パッケージ

はじめに

単位付きの数値を (物理)量 ((Physical) Quantity)といいます。
私たち技術者は日々、たくさんの量と付き合っていて、量の単位を変換したり、異なる単位で表された量同士を計算したりしています。しかし、算法言語 programming language の「数」は単位を持たない数値のみなので、算譜 program は数同士の計算の記述に留め、単位はコメントやノートに書いておくことが多いのではないでしょうか？ 量をそのまま扱う手法があれば、見通しがよくなりなるはずです。

ここでは、Julia言語で、量の算術を支援する Physical パッケージを紹介します。

インストール

Physical.jl パッケージの本家は https://github.com/ggggggggg/Physical.jl です。
Julia言語の公式パッケージではないので、直接 github からインストールします。

Pkg.clone("https://github.com/ggggggggg/Physical.jl.git")

パッケージを使うには using で読み込みます。

julia> using Physical

簡単な例から

本パッケージでも、単位付き数値(量)は、数値と単位を掛け算したものです。接頭辞 (Micro, Milli, Kilo など) をつける場合は、接頭辞と単位を括弧 () で囲みます。

julia> 1.0 * Meter
1.0 m 

julia> 1000.0 * (Milli*Meter)
1000.0 mm 

比較演算子 == や近似比較関数 isapprox を用いて、量同士を比較できます。
単位は異なっても同じ量であれば真と判定されます。次元が異なる量を比較すると例外が発生します。

julia> 1.0 * Meter == 1000.0 * (Milli*Meter)
true

julia> 0.9 * Meter == 1000.0 * (Milli*Meter)
false

julia> (1.0 + 1e-8) * Meter == 1000.0 * (Milli*Meter)
false

julia> isapprox( (1.0 + 1e-8) * Meter , 1000.0 * (Milli*Meter) )
true

julia> 1.0 * Second == 1000.0 * (Milli*Meter)
ERROR: AssertionError:
 in == at C:\Users\ ___ \.julia\v0.4\Physical\src\Quantities.jl:122

量の大きさ(数字)と単位を取り出すには .value と .unit をそれぞれ用います。
.unit の結果は、文字列型ではなく PUnits.Unit 型です。

julia> (1.0 * Meter).value
1.0

julia> (1.0 * Meter).unit
m 

julia> typeof(ans)
PUnits.Unit

julia> (1000.0 * (Milli*Meter)).value
1000.0

julia> (1000.0 * (Milli*Meter)).unit
mm 

julia> (1.0 * Meter).unit == (1000.0 * (Milli*Meter)).unit
false

同じ次元の量は加減算できます。次元が異なる量を加減算すると、例外が発生します。

julia> 1000.0*(Milli*Meter) + 0.1*Meter
1100.0 mm 

julia> 1000.0*(Milli*Meter) + 0.1*Gram
ERROR: incompatible base units kg  and m 
 in error at error.jl:21

基本単位として、質量(重さ)、長さ、時間、電流、温度、物質量を知っておけばよいでしょう。単位はフルスペルで書きます。Julia の流儀に従い、定数の頭文字は大文字にします。

julia> Kilogram
1 kg  

julia> Gram
1 g  

julia> Meter
1 m  

julia> Second
1 s  

julia> Ampere
1 A  

julia> Kelvin
1 K  

julia> Mole
1 mol  

組立単位

単位同士を乗除すると組立単位を作れます。

julia> 1.0 * Meter / Second
1.0 s⁻¹m  

量同士は乗除できます。単位も含めて計算できます。結果が無次元になると、数字型 Float や Complex になります。

julia> (1.0*Meter) / (1.0*Second)
1.0 s⁻¹m 


julia> v=(1.0*Meter)^3
1.0 m³

julia> v^(1/3)
1.0 m  

julia> v^(2/3)
1.0 m²

julia> (1.0*Meter)/(1.0*Meter)
1.0

julia> typeof(ans)
Float64

julia> Complex(1.0,1.0)*Meter / (1.0*Meter)
1.0 + 1.0im

julia> typeof(ans)
Complex{Float64}

単位の変換

単位の変換には as を用います。第二引数が変換先の単位です。変換先は組立単位でも構いません。
変換できない単位を指定すると例外が発生します。

julia> as( 1000.0 * (Milli*Meter), Meter)
1.0 m 

julia> as( 1000.0 * (Milli*Meter), Second)
ERROR: incompatible base units m  and s 
 in error at error.jl:21

エネルギーの単位

$\textrm{J}$ (joule, ジュール)はエネルギーの単位です。joule に等価な組立単位が複数あります。

julia> (1.0 * KiloGram)* (1.0*Meter/Second)^2
1000.0 g s⁻²m²

julia> as( ans, Joule )
1.0 J 

julia> (1.0*Volt)*(1.0*Coulomb)
1.0 V C 

julia> as( ans, Joule )
1.0 J 

定義済の単位や型

本パッケージには、多数の単位や定数が定義されています。定義ファイルは、data / default ディレクトリ (github のソースでは https://github.com/ggggggggg/Physical.jl/tree/master/data/default ) にあります。
以下の、4つのファイルがインクルードされているので、中身を見てみるとよいでしょう　(なお b_english.jl の定義は、現在 exportされていないので使えません)。

julia> Physical.loaded_files
4-element Array{ByteString,1}:
 "a_prefix.jl"
 "a_si_plus.jl"
 "b_english.jl"
 "c_physics.jl"

エネルギーの単位: 電子ボルト

電磁気学や電気電子工学では、エネルギーを電子ボルト(electron volt) で表示する場合があります。

Julia> 1.0 * ElectronVolt
1.0 eV 

Julia> as( ans, Joule)
1.602176565e-19 J 

新しい派生単位の作成

新しく派生単位を定義するには、DerivedUnit を用います。第一変数は、新しい派生単位の文字列表現です。例で説明しましょう。

日本の長さの単位

日本の尺貫法の長さ・面積の単位を作ってみましょう。

julia> const Shaku = DerivedUnit( "尺", 10 // 33 * Meter)
1 尺

julia> const KenJp = DerivedUnit( "閒", 6. * Shaku)
1 閒

julia> const Tsubo = DerivedUnit( "坪", KenJp ^2 )
1 坪 

julia> as( 30.* Tsubo, Meter^2 )
99.17355371900828 m²

体積の単位 リットル

体積の単位 リットル (liter) を定義しましょう。
1リットルは 一辺 $10~\textrm{cm}$ の立方体(サイコロ)の体積です。 $1~\textrm{dm} = 10^{-1}~\textrm{m} = 10~\textrm{cm}$ 。
$1~\textrm{L} = 1~\textrm{dm}^3 = (1~\textrm{dm})^3$ 。

julia> const Liter = DerivedUnit( "L", (Deci*Meter)^3 )
1 L 

julia> (10.*(Centi*Meter))^3
1000.0 cm³

julia> as( ans, Liter)
1.0 L 

圧力の単位

$\textrm{Pa}$ (pascal, パスカル)は圧力の単位です。
圧力とは、単位面積当たりに加わる力です。$\textrm{Pa}=\frac{\textrm{N}}{\textrm{m}^2}$

1気圧を定義してみましょう。1気圧は 1013.25 hPa (ヘクトパスカル)です。

julia> const Atmosphere = DerivedUnit("atm", 1013.25 (Hecto*Pascal) )

julia> 1.0 * Atomsphere
1.0 atm

julia> as( ans, Pascal)
101325.0 Pa  

julia> as(ans, Mega*Pascal)
0.101325 MPa  

psi という圧力の単位を知っていますか？ pound-force per square inch の頭文字を取ったもので、「一辺 1 inch の正方形に 1 pound の荷重が印加された」圧力に対応します。米国はヤードポンド法を使っているので、米国発祥の科学技術分野 (特に航空宇宙分野)に関わると慣れざるをえません。
1 inch = 25.4 mm、1 pound = 453 g　(ハンバーガーなどの、クォーターパウンダーは $\frac{1}{4}$ pound = 113 g)。 g_earth_gravityは、地上における重力加速度です ( c_physics.jl に定義されています)。

julia> const Inch = DerivedUnit("in", 254//10000*Meter)
1 in 

julia> const Pound = DerivedUnit("lb", 453.59237*Gram)
1 lb 

julia> as(0.25*Pound, Gram)
113.3980925 g 

julia> const Psi = DerivedUnit("psi", Pound * g_earth_gravity / Inch^2)
1 psi 

julia> as( 1.0*Psi, Pascal )
6894.757293168362 Pa 

1気圧は何psi かな？

julia> 1.0 * Atomsphere
1.0 atm

julia> as( ans, Psi)
14.695948775513449 psi 

単位付き数値ベクトルの利用

数値のコレクションに単位を付与できます。数値ベクトルや linspace 型に使えます。

julia> [ 0., 1., 2. ] * Meter
[0.0,1.0,2.0] m 

単位付き数値ベクトルの計算

一次元運動の数値解を求めてみましょう。

球を鉛直上向きに放り投げたとき、その球が鉛直下向きの重力のみを感じて運動するとします。
球の速度 $v$ と高さ $y$ は、以下の式で表されます ($g$ は重力加速度)。
$$ v = v_0 - g t ，$$
$$ y = v_0 t - \frac{1}{2}g t^2 ．$$
ただし、時刻 $t=0~\textrm{s}$における速度を $v_0$、高さを $y = 0~\textrm{m}$ としました。

$v$ と $y$ を算出する時刻 $t$ のベクトルを作ります。

julia> ts = linspace(0,2)  * Second
linspace(0.0,2.0,50) s 

初速度を、次のようにしました。

julia> v0=13.* Meter/Second
13.0 s⁻¹m 

時刻 $t$ における速度 $v$ と高さ $y$ を計算します。上の式をそのまま書けばよいですね。$.*$ は、ベクトルの要素同士の乗算です。

julia> vs = v0 - g_earth_gravity .* ts
linspace(13.0,-6.613299999999999,50) s⁻¹m 

julia> ys = v0 .* ts - g_earth_gravity * ts .* ts / 2.
[0.0,0.522443,1.02855,1.51832,1.99175,2.44884,2.8896,3.31401,3.72209,4.11384  ……
  8.1544,8.02334,7.87594,7.71221,7.53213,7.33572,7.12297,6.89389,6.64846,6.3867]
 m 

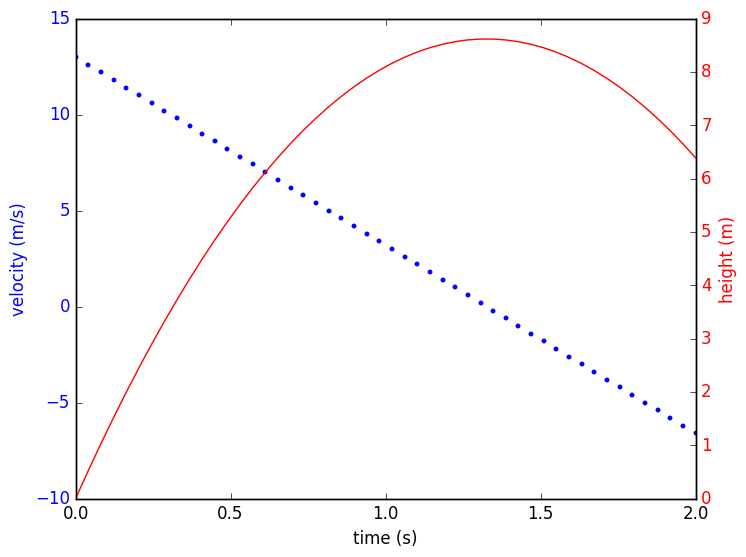
PyPlot を用いて $v(t)$, $y(t)$ をグラフに描きましょう。
PyPlot は、Python の 2次元プロットライブラリ matplotlibを Juliaから使うためのパッケージです。
matplotlibでダブルYグラフ (x軸が共通で、y軸が左右にあるグラフ)を描くサンプルプログラムが api example code: two_scales.py にあります。
これを Juliaで実装しましょう。量の数字部分を取り出すには .value を使うのでした。

using PyPlot
plot( ts.value ,vs.value, "b.")
ax1 = gca()
ax1[:set_xlabel]("time (s)")
ax1[:set_ylabel]("velocity (m/s)", color="b")
for t1 in ax1[:get_yticklabels]()
    t1[:set_color]("b")
end
ax2 = ax1[:twinx]()
ax2[:plot](ts.value, ys.value, "r-")
ax2[:set_ylabel]("height (m)", color="r")
for tl in ax2[:get_yticklabels]()
    tl[:set_color]("r")
end

なお、PyPlotで matplotlib の任意の関数を呼ぶ方法は、拙文で紹介しました。

• Qiita: 決定版？「Juliaでジュリア集合を描く」http://qiita.com/tenfu2tea/items/6bcbdd7586ea070cc25d
• Drawing Julia sets in Julia language matplotllib, APIの呼出し http://nbviewer.ipython.org/gist/tenfu2tea/fb8741db797aa42b6585#matplotllib-API%E3%81%AE%E5%91%BC%E5%87%BA%E3%81%97

まとめ

以上、Physical パッケージの機能を紹介しました。
本パッケージは、Julia のコマンドライン (REPL)を、量の電卓として使うのに十分な機能を提供します。ぜひ試してみてください。