はじめに
Julia Advent Calendar 2019 の 10日目です。
今年のプレゼントは、Grassmann.jl パッケージです。これを用いて、Juliaを外積代数の電卓にしましょう。外積代数を用いると、多次元空間の量を首尾よく記述できます。
ベクトルと行列
ベクトルと行列を、数学と似た記法で書けるのが、Julia の利点の一つです。
列ベクトルを作るには、[ ] の中に、カンマ , または改行で区切って、数(要素)を列挙します(関数 vcat() が内部で呼ばれます)。結果は、要素が縦に並んで印字されます。
julia> u=[2,1]
2-element Array{Int64,1}:
2
1
julia> w=[1
-2]
2-element Array{Int64,1}:
1
-2
julia> c=vcat(2,-1)
2-element Array{Int64,1}:
2
-1
ベクトルの要素は、ベクトルの直後に、 [ ] で囲んで添字を書いて指定します。添字は、1 から数え始めます。
julia> u[1]
2
julia> w[2]
-2
行列を作るには、同じ行の要素を空白で区切って列挙します。行を変えるには、セミコロン , または改行を挿入します。結果は、要素が縦横に並んで印字されます。
julia> u1=[2 0; 0 1]
2×2 Array{Int64,2}:
2 0
0 1
julia> w1=[0 1
2 0]
2×2 Array{Int64,2}:
0 1
2 0
行列の要素を指定するのも、ベクトルと同様に、数学と似た書き方です。
julia> u1[1,2]
0
julia> u1[1,1]
2
julia> w1[2,1]
2
縦ベクトルを水平方向に連結して、行列 $\begin{bmatrix} \mathbf{u} & \mathbf{w} \end{bmatrix}$ を作るには、[u w] または hcat(u,w) と書けばよいのです。
julia> uw=[u w]
2×2 Array{Int64,2}:
2 1
1 -2
julia> hcat(u,w)
2×2 Array{Int64,2}:
2 1
1 -2
「線形結合」を、どう書くか
線形結合は、複数のベクトルにそれぞれ係数を乗じて加えた式
$$c_1 \mathbf{u} + c_2 \mathbf{w}\tag{1}$$
です。上の式も、Julia で、そのまま書けます。
julia> c[1]*u .+ c[2]*w
2-element Array{Int64,1}:
3
4
ベクトル同士の加算には、演算子 .+ を使うことに注意します。
線形結合は、複数の書き方がありえます。(1)式は、係数ベクトル
\mathbf{c} = \begin{bmatrix}c_1 \\ c_2\end{bmatrix}
を用いて、次のようにも書けます。
\begin{bmatrix} \mathbf{u} & \mathbf{w} \end{bmatrix} \begin{bmatrix}c_1 \\ c_2\end{bmatrix} = \begin{bmatrix} \mathbf{u} & \mathbf{w} \end{bmatrix} \mathbf{c} \tag{2}
この (2) 式も、Julia で、そのまま書けます。
julia> [u w] * c
2-element Array{Int64,1}:
3
4
行列とベクトル(行列)の積を、Julia では演算子 * で書き表します。
(1)式は、係数ベクトル $c$ を使って、以下のように書いてもよいでしょう。
julia> sum(c.*(u,w))
2-element Array{Int64,1}:
3
4
演算子 .* は、配列(ベクトルや行列)の対応する要素の積からなる配列を計算します。(u,w) はタプルですから、この計算は sum(c[1]*u,c[2]*w) したがって、(1)式と同じです。
この簡潔な表現は、線形代数を広く扱う場合に、おすすめです。
例えば、$2\times 2$ 行列は、線形性を満たすので「ベクトル」です。さて、ひとつ上の書き方で、$2\times 2$ 行列を水平に連結しようとして [m1 m2] と書くと、2x2 ではなく 2x4の行列が作られてしまい、そのあと「ベクトルを連結した行列」と係数ベクトルの積が計算できません。
julia> m1=[2 0; 0 1]
2×2 Array{Int64,2}:
2 0
0 1
julia> m2=[0 1; 2 0]
2×2 Array{Int64,2}:
0 1
2 0
julia> [m1 m2]
2×4 Array{Int64,2}:
2 0 0 1
0 1 2 0
julia> [m1 m2] * c
ERROR: DimensionMismatch("matrix A has dimensions (2,4), vector B has length 2")
しかし、(1)式に基づく書き方なら、線形結合を、正しく計算できます。
julia> c[1]*m1 .+ c[2] * m2
2×2 Array{Int64,2}:
4 -1
-2 2
julia> sum(c.*(m1,m2))
2×2 Array{Int64,2}:
4 -1
-2 2
外積代数
外積代数するために、Grassmann.jl パッケージを導入しましょう。
REPLのパッケージ・マネージャで導入できます。
(v1.1) pkg> add Grassmann
using Grassmann
2次元の外積代数
外積代数は、くさび積(wedge product) $\wedge$ を導入します。
2次元の単位ベクトルを
\mathbf{v}_1 = \begin{bmatrix} 1 \\ 0\end{bmatrix}, \mathbf{v}_2 = \begin{bmatrix} 0 \\ 1\end{bmatrix}
と書きましょう(数学では 文字 $\mathbf{e}$ を当てることが多いですが、Grassmann.jl パッケージに合わせます)。
くさび積 $\wedge$ は、以下の性質を持ちます。(以下、ベクトルの bold font が意図通りに指定できなかった箇所があります。)
■ v1 または v2 と スカラー $1$ とのくさび積は、それ自身です。
\mathbf{v}_1 \wedge 1 = \mathbf{v}_1, \\
\mathbf{v}_2 \wedge 1 = \mathbf{v}_2
■ v1 または v2 と自身とのくさび積は スカラー $0$ です。
\mathbf{v}_1 \wedge \mathbf{v}_{1} = \mathbf{v}_2 \wedge \mathbf{v}_{2} = 0
■ くさび積の左右の入れ替えは、符号が変わります。
\mathbf{v}_1 \wedge \mathbf{v}_2 = -\mathbf{v}_2 \wedge \mathbf{v}_1 \equiv \mathbf{v}_{12} (\textrm{と名付けます})
■ v1 または v2 と v12 とのくさび積は $0$ です。
\mathbf{v}_1 \wedge \mathbf{v}_{12} = \mathbf{v}_1 \wedge (\mathbf{v}_1 \wedge \mathbf{v}_{2}) = 0, \\
\mathbf{v}_2 \wedge \mathbf{v}_{12} = \mathbf{v}_2 \wedge (\mathbf{v}_1 \wedge \mathbf{v}_{2}) = 0
■ ■
さて、2次元の外積代数の「枠」(frame, 枠の順序を無視したものが「底」basis です)は、以下の4つです。
1, \mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_{12}
すなわち、2次元の外積代数の元は、上の線形結合となります。
c_1 1 + c_2 \mathbf{v}_1 + c_3 \mathbf{v}_2 + c_4 \mathbf{v}_{12}
2次元空間のベクトル
\mathbf{u} = \begin{bmatrix} u_1 \\ u_2\end{bmatrix}, \mathbf{w} = \begin{bmatrix} w_1 \\ w_2\end{bmatrix}
を外積代数の元とみなしましょう。
\mathbf{u} = u_1 \mathbf{v}_1 + u_2 \mathbf{v}_2, \\
\mathbf{w} = w_1 \mathbf{v}_1 + w_2 \mathbf{v}_2
$\mathbf{u}$ と $\mathbf{w}$ のくさび積 $\mathbf{u}\wedge\mathbf{w}$ は
\mathbf{u}\wedge\mathbf{w} = (u_1 w_2 - u_2 w_1) \mathbf{v}_{12} \tag{3}
のように計算されます。 $(u_1 w_2 - u_2 w_1)$ は、ベクトル $\mathbf{u}$ と $\mathbf{w}$ で張られる平行四辺形の面積です($\mathbf{u}$ を反時計方向に回転すると $\mathbf{w}$ の向きになるときは正、逆のときは負の値になります)。$\mathbf{v}_{12}$ は面積要素を意味する記号とも読めます。
上のくさび積は、3次元空間ベクトルの外積(クロス積 cross product)と同等です。
3次元空間の$xy$平面に、ベクトルを
\mathbf{u} = \begin{bmatrix} u_1 \\ u_2 \\ 0\end{bmatrix},
\mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \\ 0\end{bmatrix}
のように埋め込むと、ベクトル $\mathbf{u}$ と $\mathbf{w}$ の外積(クロス積)は
\mathbf{u}\times\mathbf{w} = (u_1 w_2 - u_2 w_1) \mathbf{v}_{3} \tag{4}
と計算されます。ここで
\mathbf{v}_3 = \begin{bmatrix} 0 \\ 0 \\ 1\end{bmatrix}
は $z$ 方向の単位ベクトルです。
(3)式の $v_{12}$ が、(4)式では $v_{3}$ に置き換わっています。
2次元の外積代数:Juliaで書く
2次元の外積代数は、Λ(2) で作成できます (Λ は、ギリシャ文字のラムダの大文字です。Julia のREPLや Jupyter notebook入力セルで入力するには、(バックスラッシュ) \ Lambda の後にTABキーを押します。(このような Unicode入力補間について、小記事を以前書きました。→
[Julia] UTF-8 表記の演算子たち )
julia> G2=Λ(2)
Grassmann.Algebra{⟨++⟩,4}(v, v₁, v₂, v₁₂)
外積代数 G2 の枠は、v, v₁, v₂, v₁₂ と表されます。 v は、スカラー 1 に対応します。
julia> G2.v
v
julia> G2.v1
v₁
julia> G2.v2
v₂
julia> G2.v12
v₁₂
くさび積の記号 ∧ を入力するには、\ wedge の後にTABキーを押します。ギリシャ文字のラムダの小文字 λ とは異なります。(こちらを入力するには、 \ lambda の後にTABキー押します)
くさび積を用いて、平行四辺形の面積を求めてみます。
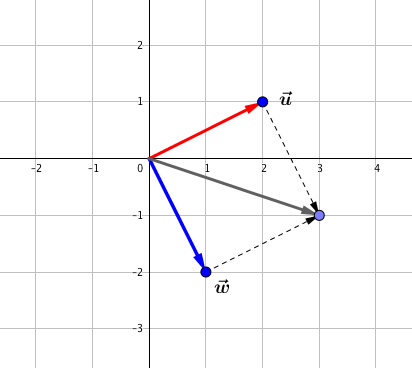
冒頭のベクトル u と w を例にします。
冒頭の u と v を、Grassmann.jl の元にしましょう。G2.v1 と G2.v2 で線形結合すればよいです。
julia> u2=[2,1]
2-element Array{Int64,1}:
2
1
julia> w2=[1
-2]
2-element Array{Int64,1}:
1
-2
julia> u=sum(u2.*(G2.v1,G2.v2))
2v₁ + 1v₂
julia> w=sum(w2.*(G2.v1,G2.v2))
1v₁ - 2v₂
w と u のくさび積を求めましょう。
julia> w∧u
5v₁₂
julia> norm(w∧u)
5.0
平行四辺形の面積は 5 と算出されました。
実は、u と w は直交しており(内積が 0)、ノルムは等しく $\sqrt{5}$ です。
julia> u2⋅w2
0
julia> @show norm(u2), norm(w2)
(norm(u), norm(w)) = (2.23606797749979, 2.23606797749979)
(2.23606797749979, 2.23606797749979)
前節末尾で触れたように、3次元空間の $xy$ 平面に埋め込んで、ベクトル積を計算しても同じ結果が得られることを確かめましょう。
$\mathbf{u}, \mathbf{w}$ の $z$成分に 0 を付け加えます。
julia> u3=[u2;0]
3-element Array{Int64,1}:
2
1
0
julia> w3=[w2;0]
3-element Array{Int64,1}:
1
-2
0
ベクトルの外積(クロス積)は、演算子 × を使います (× を入力するには、(バックスラッシュ) \ times の後にTABキーを押します)。LinearAlgebra パッケージを予め読み込んでおきます。
julia> using LinearAlgebra
julia> w3×u3
3-element Array{Int64,1}:
0
0
5
同じ面積が得られました。
ところで、昨年(2018年)の Julia Advent Calendar で、単位付き数字を扱う Unitful パッケージを紹介しました(→ Julia 1.0で単位付き数値の算術 - Unitful パッケージ )。
G2 代数は、単位付き数字でも使えます。
長さの単位 u"m" を、ベクトルに与えてみましょう。
julia> using Unitful
julia> u=sum((u2*1u"m").*(G2.v1,G2.v2))
2v₁ + 1v₂ m
julia> w=sum((w2*1u"m").*(G2.v1,G2.v2))
1v₁ - 2v₂ m
julia> w∧u
0 + 5v₁₂ m^2
julia> norm(w∧u)
5.0v m^2
くさび積は、面積の単位 $\mathrm{m}^{2}$を持ちました。
ノルム norm をとると、スカラー v が出てきました。
3次元の外積代数
3次元の単位ベクトルを
\mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \\ 0\end{bmatrix}, \mathbf{v}_2 = \begin{bmatrix} 0 \\ 1 \\ 0\end{bmatrix}, \mathbf{v}_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix}
と書きましょう。
これらのくさび積のうち、非零の値を持つのは、次の 3つだけです($\wedge$ の左右を交換すると、符号が変わりますが、独立な値としては、以下の3つを選べばよろしいです)。
\mathbf{v}_1 \wedge \mathbf{v}_2 \equiv \mathbf{v}_{12}, \\
\mathbf{v}_1 \wedge \mathbf{v}_3 \equiv \mathbf{v}_{13}, \\
\mathbf{v}_2 \wedge \mathbf{v}_3 \equiv \mathbf{v}_{23}
また、3つのベクトルのくさび積のうち、非零の値を持つのは
\mathbf{v}_1 \wedge \mathbf{v}_2 \wedge \mathbf{v}_3 \equiv \mathbf{v}_{123}
のみです (ベクトルを入れ替えると符号が変わる場合がありますが、上の値を選んでおけばよろしいです)。
さて、3次元の外積代数の「枠」は、以下の 8つとなります。
1, \\
\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3, \\
\mathbf{v}_{12}, \mathbf{v}_{13}, \mathbf{v}_{23}, \\
\mathbf{v}_{123}
すなわち、3次元の外積代数の元は、上の線形結合となります。
3次元ベクトル $\mathbf{s}, \mathbf{t}, \mathbf{u}$ を、外積代数の元とみなしましょう。
$\mathbf{s}$ と $\mathbf{t}$ とのくさび積は、ベクトル $\mathbf{s}$ と $\mathbf{t}$ で張られる平行四辺形の面積を表します。同様に、$\mathbf{s}$ と $\mathbf{u}$ とのくさび積、$\mathbf{t}$ と $\mathbf{u}$ とのくさび積も、同様に、それらが張る平行四辺形の面積を表します。
3つのベクトル $\mathbf{s}$, $\mathbf{t}$, $\mathbf{u}$ のくさび積 $\mathbf{s} \wedge \mathbf{t} \wedge \mathbf{u}$ は $\mathbf{v}_{123}$ のスカラー倍になります。
その倍数は、$\mathbf{s}$, $\mathbf{t}$, $\mathbf{u}$ で張られる平行六面体の体積を表します。この体積は、3次元空間ベクトルの外積(クロス積)と内積を使って使、$(\mathbf{s}×\mathbf{t})⋅\mathbf{u}$ と計算されます。
3次元の外積代数:Julia で書く
3次元の外積代数は、Λ(3) で作成できます。
julia> G3=Λ(3)
Grassmann.Algebra{⟨+++⟩,8}(v, v₁, v₂, v₃, v₁₂, v₁₃, v₂₃, v₁₂₃)
枠が、v, v₁, v₂, v₃, v₁₂, v₁₃, v₂₃, v₁₂₃ で表されます。
以下のような、3次元ベクトル $\mathbf{s}, \mathbf{t}, \mathbf{u}$ を例にします。
julia> s3=[2, 1, 0]
3-element Array{Int64,1}:
2
1
0
julia> t3=[-2, 2, 1]
3-element Array{Int64,1}:
-2
2
1
julia> u3=[2, 0, 2]
3-element Array{Int64,1}:
2
0
2
これらを、Λ(3) の元にしましょう。G3.v1, G3.v2, G3.v3 で線形結合します。
julia> s=sum(s3.*(G3.v1,G3.v2,G3.v3))
2v₁ + 1v₂ + 0v₃
julia> t=sum(t3.*(G3.v1,G3.v2,G3.v3))
-2v₁ + 2v₂ + 1v₃
julia> u=sum(u3.*(G3.v1,G3.v2,G3.v3))
2v₁ + 0v₂ + 2v₃
■ 3つのうちの2個のくさび積と、ベクトルの外積(クロス積)を両方計算しましょう。
julia> s∧t
6v₁₂ + 2v₁₃ + 1v₂₃
julia> norm(s∧t)
6.4031242374328485
julia> s3×t3
3-element Array{Int64,1}:
1
-2
6
julia> norm(s∧t)
6.4031242374328485
julia> s∧u
1v₁₂ + 2v₁₃ + 2v₂₃
julia> s3×u3
3-element Array{Int64,1}:
2
-2
1
julia> t∧u
-4v₁₂ - 6v₁₃ + 4v₂₃
julia> t3×u3
3-element Array{Int64,1}:
4
6
-4
ベクトルの外積(クロス積 cross product)$\times$ とくさび積 $\wedge$ との間で、以下のような対応が読み取れます。
\mathbf{v}_{23} \longleftrightarrow \begin{bmatrix} 1 \\ 0 \\ 0\end{bmatrix} = \mathbf{v}_1, \\
\mathbf{v}_{13} \longleftrightarrow \begin{bmatrix} 0 \\ -1 \\ 0\end{bmatrix} = -\mathbf{v}_2, \\
\mathbf{v}_{12} \longleftrightarrow \begin{bmatrix} 0 \\ 0 \\ 1\end{bmatrix} = \mathbf{v}_3
■
実は、外積代数の世界では、 くさび積を含まない値
\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}
と、くさび積を1個だけ含む値
\mathbf{v}_{12}, \mathbf{v}_{13}, \mathbf{v}_{23}
は、異なる種類に属します。
ベクトルの外積(クロス積)は、この違いを無視し、外積の結果を 3次元空間に落とし込んでいます。
そのため、3次元空間の代数で閉じますが、線分(ベクトル)と面積要素が、同じ見かけに混在するという居心地が悪いものになっています。
■ 次に、$\mathbf{s}$, $\mathbf{t}$, $\mathbf{u}$ で張られる平行六面体の体積を求めましょう。
julia> s∧t∧u
0 + 14v₁₂₃
julia> norm(s∧t∧u)
14.0
julia> (s3×t3)⋅u3
14
体積要素 $\mathbf{v}_{123}$ がスカラー $1$ に対応しました。
終わりに
以上、Julia を、外積代数の電卓にする方法を、駆け足で紹介しました。2次元、3次元しか紹介していませんが、4次元以上も同様に展開できます。
上に紹介したのは、Grassmann.jl パッケージの、ごく小さい機能です。
このパッケージの対象は、微分幾何学です。微分幾何の対象は、微小な線要素 $\mathrm{d}x$、微小な面積要素 $\mathrm{d}x\wedge\mathrm{d}y$ 、微小な体積要素 $\mathrm{d}x\wedge\mathrm{d}y\wedge\mathrm{d}z$ などからなる世界です。
物理で扱う物理量を微分幾何の言葉で書くと、その性質が明確に表現できます。物理量を外積代数で扱う方法を解説した日本語の書籍が続々と出版されるようになりました。単に数式表現だけではなく、微分幾何の対象のまま数値計算することも日常になることでしょう。
最後に思わせぶりを。
julia> G3=Λ(3)
Grassmann.Algebra{⟨+++⟩,8}(v, v₁, v₂, v₃, v₁₂, v₁₃, v₂₃, v₁₂₃)
Λ(3) を定義したときに出現した ⟨+++⟩ は計量を表しています。物理の場の理論では色々な計量(たとえば、4次元の (-+++) )を扱います。Grassmann.jl は、これら計量を自由に扱える柔軟性を持っています。興味のある方は、Grassmann.jl の README や、JuliaCon 2019 の発表 Geometric algebra in Julia with Grassmann.jl 、Youtube を覗いてみるとよいでしょう。
とても1回の解説では収まりません。また、別の機会に書きたいと思います。