前書き
本記事では、Quantum Katas の GHZ game について解説します。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。
前回から引き続き、今回も同じような設定の GHZ ゲームを学んでいきます。CHSH ゲームをやっていない方は、先にこちらを参照してください。
GHZ ゲームとは
CHSH ゲームに引き続き、Quantum katas からもリンクされている この資料 (Waterloo 大学の Watrous 教授のページ) を見るのが良さそうです。GHZ ゲームをまとめると以下になります。
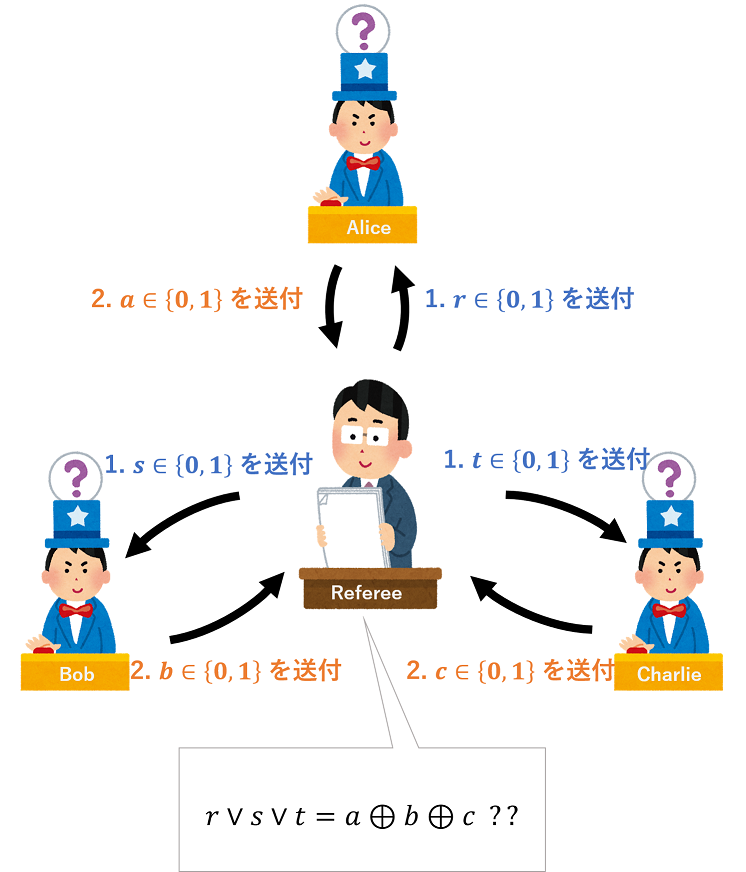
- 登場人物は、アリス、ボブ、チャーリー、審判の 4 名。
- アリス、ボブ、チャーリーが協力し、審判と対決する。
- 審判はアリスに値 $r \in \{0, 1\}$、ボブに値 $s \in \{0, 1\}$、チャーリーに $t \in \{0, 1\}$ を送る。
- ただし、$rst = \{000,011,101,110\}$ を満たす。
- アリス、ボブ、チャーリーはそれぞれ回答 $a, b, c \in \{0, 1\}$ を審判に送る。
- $a \oplus b \oplus c= r \lor s \lor t$ が満たされればアリス、ボブ、チャーリーの勝利。満たされなければ審判の勝利。
- 審判が値を送る前は、アリス、ボブ、チャーリーはあらゆる情報を共有可能。
- 値送付後はアリス、ボブ、チャーリー間のあらゆる通信は禁止される。
事前にどんな情報を共有すればアリスとボブ、チャーリーは審判に勝てるか、を考える問題ですね。プレーヤーの数や審判の質問に制限がある点が差異となっていますが、それ以外の大筋は CHSH ゲームと同じです。加えて、CHSH と同じく GHZ も著者の名字をつなげたものとなっています。Kata を発表順に問いてきた人には、GHZ 状態のほうが馴染みがあるかもしれませんね。
古典的に GHZ ゲームを考えてみよう
まずは古典的にこのゲームを考えてみましょう。何も考えずに全員がオウム返しをしたらどうなるでしょうか。このときは $000$ のときだけ勝利なので、確率は $1/4$ となります。一方、全員なにも考えずに 1 を返した場合は、勝利確率は $3/4$ になります。
もっと改善できるか考えてみましょう。アリスが $r=i$ を受け取ったときの回答を $a_i$ とします。ボブとチャーリーも同じように記載すると、以下の式が全てみたされればアリス達は 100 % 勝利できそうです。
\begin{cases}
a_0 \oplus b_0 \oplus c_0 &= 0 \\
a_0 \oplus b_1 \oplus c_1 &= 1 \\
a_1 \oplus b_1 \oplus c_0 &= 1 \\
a_1 \oplus b_0 \oplus c_1 &= 1
\end{cases}
大変残念なことに、この 4 つの方程式を全て足すと、$0=1$ が得られます。矛盾しちゃっているので、これは成り立たないわけですね、残念。その他の妙案もなく、このゲームを古典的に勝利するための最善策は CHSH ゲームと同様確率 3/4 しか得られないことが知られています。
量子的に GHZ ゲームを考えてみよう
続いて量子的に GHZ ゲームを改善する方法を考えます。流れは CHSH ゲームと同じなのですが、どんな差が出てくるか楽しみですね。
GHZ ゲームでは、アリス、ボブ、チャーリーは事前に以下のような 量子ビットを生成して共有します。(余談ですが、これも GHZ 状態ということがあるそうです。以前の Kata では、GHZ 状態って全部 0 と 全部 1 の重ね合わせと習ったと思うのですが…)
$$
|\psi\rangle = |\psi_{\text{Alice}}\rangle \otimes |\psi_{\text{Bob}}\rangle \otimes |\psi_{\text{Charlie}}\rangle = \frac{1}{2}(|000\rangle - |011\rangle - |101\rangle - |110\rangle )
$$
上記量子ビットを利用した、アリス/ボブ/チャーリーの戦略は以下のようなものです。全員同じ戦略を取ります。
戦略
- 受け取った値 $r$ (もしくは $s$, $t$) が 0 なら、自分の量子ビットを観測した結果をそのまま回答する。
- 受け取った値 $r$ (もしくは $s$, $t$) が 1 なら、自分の量子ビットをアダマール ゲートで処理したあとで観測した結果を回答する。
CHSH ゲームと比べると、戦略もシンプルですね。さて、どのくらいの確率で勝利できるのか考えてみましょう。審判は $rst = \{000,011,101,110\}$ の 4 つのうちからいずれかを選択するので、この 4 通りを順番に考えていけば良さそうですね。
パターン 1: $rst = 000$
まずは審判が全員に 0 を送った場合です。このときは $a \oplus b \oplus c = 0$ なら勝利です。審判から受け取った値が $0$ なら各プレーヤーは自分の量子ビットをそのまま観測した結果を返しますが、現在の状態が $\frac{1}{2}(|000\rangle - |011\rangle - |101\rangle - |110\rangle )$ を思い出すと、どの状態が観測されても上記の $a \oplus b \oplus c = 0$ は満たされることがわかります。すなわち、$000$ が来たときはアリスたちは 100 % 勝利することが可能です。
パターン 2: $rst = 011$
続いて、審判がアリスにだけ 0 を、それ以外のプレーヤーには 1 を送った場合です。このときは $a \oplus b \oplus c = 1$ なら勝利です。さて、どうなるでしょうか。このときはアリスの量子ビットだけは変わらず、それ以外のビットはアダマールで処理されることとなります。式で書けば、
$$
(I\otimes H \otimes H)|\text{GHZ}\rangle = \frac{1}{ 2}\Big(|0\rangle(H \otimes H)(|00\rangle - |11\rangle) - |1\rangle(H \otimes H)(|01\rangle + |10\rangle) \Big)
$$
となります。それぞれの項を計算すると
\begin{aligned}
|00\rangle - |11\rangle
\xrightarrow{H(0)}& \frac 1 {\sqrt 2}(|00\rangle + |01\rangle - |10\rangle + |11\rangle) = \frac {|0\rangle - |1\rangle}{\sqrt 2}|0\rangle + \frac {|0\rangle + |1\rangle}{\sqrt 2}|1\rangle \\
\xrightarrow{H(1)}& |10\rangle + |01\rangle \\
\end{aligned}
\begin{aligned}
|01\rangle + |10\rangle
\xrightarrow{H(0)}& \frac 1 {\sqrt 2}(|00\rangle - |01\rangle + |10\rangle + |11\rangle) = \frac {|0\rangle + |1\rangle}{\sqrt 2}|0\rangle - \frac {|0\rangle - |1\rangle}{\sqrt 2}|1\rangle \\
\xrightarrow{H(1)}& |00\rangle - |11\rangle \\
\end{aligned}
となるので、結果として変換後の状態は以下のように記述されます。
\begin{aligned}
(I\otimes H \otimes H)|\text{GHZ}\rangle
&= \frac{1}{ 2}\Big(|0\rangle(|10\rangle + |01\rangle) - |1\rangle(|00\rangle - |11\rangle) \Big) \\
&= \frac{1}{ 2}(|010\rangle + |001\rangle -|100\rangle + |111\rangle)
\end{aligned}
一見して分かる通り、各量子状態は 1 となる状態が 1 つもしくは 3 つ含まれていることがわかります。要するに、この量子状態はいずれが観測されたとしても、$a \oplus b \oplus c = 1$ を満たします。驚きですね。言い換えると、$rst = 011$ が審判から与えられたときは、ボブとチャーリーがアダマールゲートで処理すれば、プレーヤー達は必ずゲームに勝利することができます。文字通り完全勝利です。
パターン 3: $rst = 101, 110$
他のパターンも見ていきましょう、と言いたいところですが、その必要はありません。ここまで式変形を追った方ならすぐに分かるかも知れませんが、この GHZ 状態と問題設定は対称性があるので、ボブだけが 0 を受け取るとき、およびチャーリーだけが 0 を受け取るときのゲームの様子はアリスだけが 0 を受け取ったときと変わりません。そのため、いずれの場合もプレーヤー達は先に記した戦略を利用して必ずゲームに勝利することができます。
GHZ ゲームのまとめ
明らかではありますが、いずれの場合も 100 % 勝利することができるので、GHZ ゲームではプレーヤー達は必ず勝利することができます。よかったですね。
というわけで Task の解説に移りましょう。
Task 1.1. Win condition
問題
入力: アリス、ボブ、チャーリーが与えられる値 $rst$ 及びアリス、ボブ、チャーリーの提示する値 $abc$
出力: アリス達が勝利する ($r \lor s \lor t = a\oplus b\oplus c\oplus$ が成り立つ) なら True を、そうでないなら False を返す。
解説
CHSH ゲームのときと同じく、そのまんまですね。特に難しくありません。
function WinCondition (rst : Bool[], abc : Bool[]) : Bool {
return (rst[0] or rst[1] or rst[2]) == XOR(abc[0], XOR(abc[1], abc[2]));
}
Task 1.2. Random classical strategy
問題
入力: アリス達が受け取る値 $r, s, t \in \{0, 1\}$
出力: 古典的な戦略として、ランダムに出力値 $a, b, c \in \{0, 1\}$ を返せ。このときは 50 % の確率でアリスたちは勝利できる。
解説
まずは古典コンピューターの場合です。今回のお題はランダムに値を返せ、というものになります。これもあまり難しいものではありません。乱数については、量子ビットを使ってみました。(これはもはや量子アルゴリズムなのかも知れませんが笑)
operation RandomClassicalStrategy (input : Bool) : Bool {
body(...) {
mutable result = false;
using(q = Qubit()) {
H(q);
if(M(q) == Zero) {
set result = true;
}
Reset(q);
}
return result;
}
}
Task 1.3. Best classical strategy
問題
入力: アリス達が受け取る値 $r, s, t \in \{0, 1\}$
出力: 古典的な戦略として、最も望ましい戦略に基づき出力値 $a, b, c \in \{0, 1\}$ を返せ。このときは 75 % の確率でアリスたちは勝利できる。
解説
引き続き古典コンピューターの場合です。先の解説でも記載したとおり、何も考えずに全員が 1 を返せば 75 % で勝利できます。
operation BestClassicalStrategy (input : Bool) : Bool {
return true;
}
Task 1.4 Referee classical GHZ game
問題
入力: 各プレーヤーが取る戦略
strategyと各入力値
出力: 各プレーヤーの出力値を Array で返せ。
解説
これもそのまま返せばいいだけです。
operation PlayClassicalGHZ (strategy : (Bool => Bool), inputs : Bool[]) : Bool[] {
return [strategy(inputs[0]), strategy(inputs[1]), strategy(inputs[2])];
}
Task 2.1. Entangled triple
問題
入力: 3 つの量子ビット $|000\rangle$
ゴール: GHZ 状態 $|\psi\rangle = \frac{1}{2}(|000\rangle - |011\rangle - |101\rangle - |110\rangle )
$ を作る。
解説
続いて量子的な GHZ ゲームに入ります。まずは状態の生成ですが、結構面倒です。初期の Kata を彷彿とさせる問題ですが、位相以外の係数を省略しつつ地道に考えてみましょう。GHZ 状態から 000 に収束させるためには、
\begin{aligned}
\begin{matrix}
000 \\
-011 \\
-101 \\
-110
\end{matrix}
&\xrightarrow{\text{CNOT}(0, 2)}
\begin{matrix}
000 \\
-011 \\
-100 \\
-111
\end{matrix}
\xrightarrow{\text{H}(0)}
\begin{matrix}
100 \\
-011
\end{matrix}
\xrightarrow{\text{CNOT}(\bar 0, 1),\text{CNOT}(\bar 0, 2)}
\begin{matrix}
100 \\
-000
\end{matrix} \\
&\xrightarrow{\text{H}(0)}
-100
\xrightarrow{\text{Z}(0)}
100
\xrightarrow{\text{X}(0)}
000
\end{aligned}
みたいなプロセスを踏めば良さそうです。もっとエレガントにできる気もしますが、どうなんでしょうね。問題としては 000 から GHZ 状態を生成する問題なので、上記を逆順に処理していけば良さそうです。回答は以下です。
operation CreateEntangledTriple (qs : Qubit[]) : Unit {
body(...) {
X(qs[0]);
Z(qs[0]);
H(qs[0]);
X(qs[0]);
CNOT(qs[0], qs[1]);
CNOT(qs[0], qs[2]);
X(qs[0]);
H(qs[0]);
CNOT(qs[0], qs[2]);
}
}
Task 2.2. Quantum strategy
問題
入力: 審判から受け取る値
inputと量子もつれ状態となっている量子ビットqubit
出力: $input=0$ なら計算基底で、$input=1$ なら X 基底に対して観測を行い、結果を出力する。
解説
タイトル通り、アリス達が取る量子的な戦略です。CHSH ゲームとは異なり、全員が同じ戦略を取るので、実装も楽ですね。問題設定が X 基底で観測せよ、となっているのは CHSH ゲームでもやったとおり、Measure を使えば良さそうですね。回答は以下です。
operation QuantumStrategy (input : Bool, qubit : Qubit) : Bool {
if(input) {
return BoolFromResult( Measure([PauliX],[qubit]));
} else {
return BoolFromResult( M(qubit));
}
}
Task 2.3. Play the GHZ game using the quantum strategy
問題
入力: アリス達が量子的な戦略に従って
Bool値を出力するオペレーションの配列strategies。アリス達は既に質問 $r, s, t$ を受け取っている。
出力: アリス達の回答 $a, b, c$
解説
CHSH ゲームと同様、ゲーム自体を自分で回すのではなく、与えられた戦略に基づき出力を返すだけのオペレーションを作るという問題です。これも戦略が与えられるので、あとは呼び出した結果を返してあげれば終了です。これもタスク自体は難しくないですね。
operation PlayQuantumGHZ (strategies : (Qubit => Bool)[]) : Bool[] {
mutable result = [false, false, false];
using(qs = Qubit[3]) {
// GHZ 状態の生成
CreateEntangledTriple(qs);
for(i in 0..Length(strategies)-1) {
// 結果の代入
set result w/= i <- strategies[i](qs[i]);
}
ResetAll(qs);
}
return result;
}
まとめ
この記事では、GHZ ゲームとゲームの実装である Kata について解説しました。CHSH ゲームと同様に、量子的な戦略に基づき古典戦略ではなしえない勝利確率の向上を行うという内容でした。あとから知ったのですが、CHSH ゲームや GHZ ゲームが有名になったのはベルの不等式が破られるからで、局所性を持つ隠れた変数理論によって量子的な振る舞いを記述することが困難であることがわかる一つの実例になったから、ということのようです。こうした物理学の歴史上も意味がある内容も学べるんですねー。隠れた変数理論やベルの不等式なんかは、EMANの物理学・量子力学・ベルの不等式 が詳しいです。