Quantum Katas で始める量子コンピュータ入門 |13⟩: CHSH game

前書き

本記事では、Quantum Katas の CHSH game について解説します。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。

今回は量子力学の不思議な性質である量子もつれを利用して、審判とプレーヤー間で行われるゲームについて考えていきます。ここでいうゲームとは、いわゆるゲーム理論のゲームです。各プレーヤーは与えられた条件下で戦略を決定する、というものです。早速見ていきましょう。

CHSH ゲームとは

詳しくは Quantum katas からもリンクされている この資料 (Waterloo 大学の Watrous 教授のページ) を見るのが良さそうです。CHSH ゲームをまとめると以下になります。

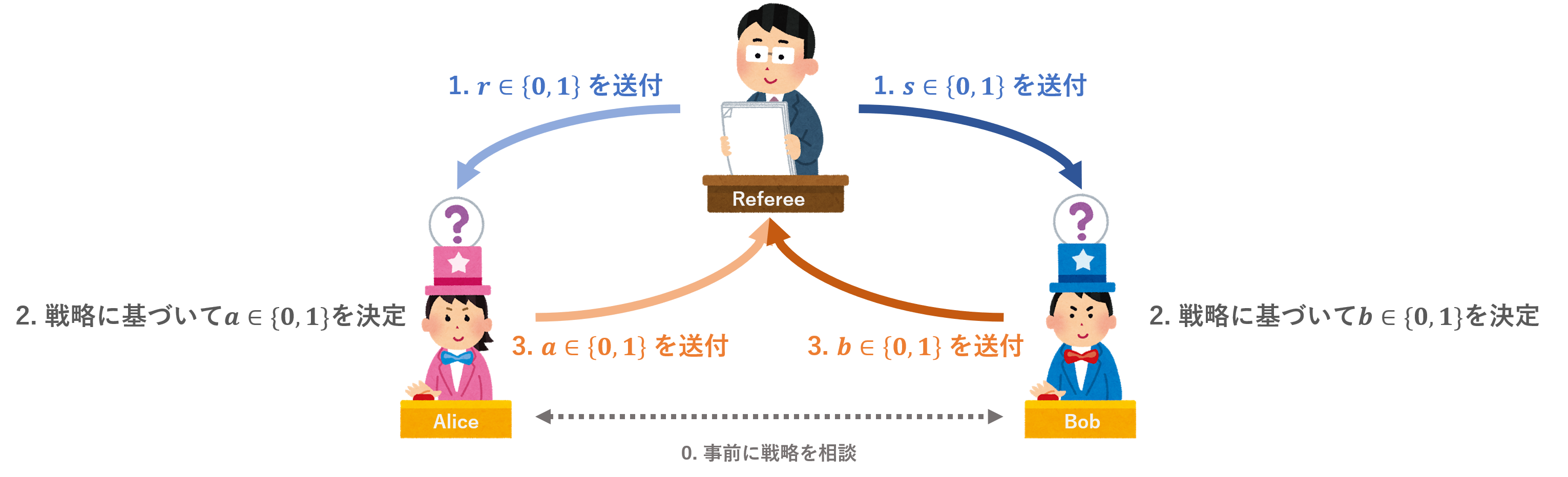
• 登場人物は、アリス、ボブ、審判の 3 名。
• アリスとボブが協力し、審判と対決する。
• 審判はアリスに値 $r \in \{0, 1\}$、ボブに値 $s \in \{0, 1\}$ を送る。
• アリスとボブはそれぞれ回答 $a, b \in \{0, 1\}$ を審判に送る。
• $a \oplus b = r \land s$ が満たされればアリスとボブの勝利。満たされなければ審判の勝利。
• 審判が値を送る前は、アリスとボブはあらゆる情報を共有可能。
• 値送付後はアリスとボブ間のあらゆる通信は禁止される。

図にするとこんな感じです。

事前にどんな情報を共有すればアリスとボブは審判に勝てるか、を考える問題ですね。ちなみに CHSH というのは 原著論文 - Proposed Experiment to Test Local Hidden-Variable Theories の著者の名字をつなげたものです。なんと出版は 1969 年…！古すぎて(？) arXiv には無いようですが、ResearchGate でダウンロードできるようなので興味がある方はぜひどうぞ。

古典的に CHSH ゲームを考えてみよう

まずは古典的にこのゲームを考えてみましょう。勝利できるパターンは以下の通りです。

表1 勝利パターン

r	s	a$\oplus$ b
0	0	0
0	1	0
1	0	0
1	1	1

例えば、アリスもボブも質問と同じ値をオウム返しするという戦略をとった場合は、勝利確率は 1/4 になりますが、アリスだけ質問を反転して返すという戦略をとった場合は、3/4 で勝利することができます。また、そんなめんどくさいことを考えずとも、真理値表上で 0 となる確率が 3/4 なのだから、アリスもボブも常に 0 を返した場合でも勝利確率は 3/4 となります。(審判はランダムに質問を生成すると仮定しています。)その他の妙案もなく、このゲームを古典的に勝利するための最善策でも確率 3/4 しか得られないことが知られています。

量子的に CHSH ゲームを考えてみよう

続いて量子的に CHSH ゲームを改善する方法を考えます。これもこれまでやってきた各アルゴリズムと同じで、私を含めた一般人にとっては自分で考えてどうにかなるものではないので、先の PDF 資料をもとに進めていきましょう。

まず、アリスとボブは事前に量子ビットでベル状態を作成し、1 ビットずつ共有しておきます。

$$
|\psi\rangle = |\psi_{\text{Alice}}\rangle \otimes |\psi_{\text{Bob}}\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)
$$

加えて、角度 $\theta \in [0, 2\pi)$ を使って状態 $|\phi_0(\theta)\rangle$ と $|\phi_1(\theta)\rangle$ を

\begin{align}
    |\phi_0(\theta)\rangle &= \cos \theta |0\rangle + \sin \theta |1\rangle \\
    |\phi_1(\theta)\rangle &= -\sin \theta |0\rangle + \cos \theta |1\rangle
\end{align}

と定義します。

この定義を用いてアリスとボブが取る戦略は以下の通りです。

アリスの戦略

• アリスが受け取った値 $r$ が 0 なら、アリスは $\{|\phi_0(0)\rangle, |\phi_1(0)\rangle\}$ を基底とした観測を行った結果 $a$ を返す。
• アリスが受け取った値 $r$ が 1 なら、アリスは $\{|\phi_0(\pi/4)\rangle, |\phi_1(\pi/4)\rangle\}$ を基底とした観測を行った結果 $a$ を返す。

ボブの戦略

• ボブが受け取った値 $s$ が 0 なら、アリスは $\{|\phi_0(\pi/8)\rangle, |\phi_1(\pi/8)\rangle\}$ を基底とした観測を行った結果 $b$ を返す。
• ボブが受け取った値 $s$ が 1 なら、アリスは $\{|\phi_0(-\pi/8)\rangle, |\phi_1(-\pi/8)\rangle\}$ を基底とした観測を行った結果 $b$ を返す。

うーん、この時点ではそーなんだくらいにしか思えませんね。そうは言われても、というのが個人的な感想でした。上記のような戦略で本当に勝利できるのでしょうか？ また、その勝利確率はどのくらいになるのでしょうか。確かめてみましょう。

勝利する条件を地道に計算する

アリスとボブが勝利できる組み合わせの条件は表 1 に示したとおり、4 パターンがあります。勝利する確率は、表1に示した勝利条件が満たされる確率を足し算したものになるので、順番に考えてみましょう。また、計算のために各基底の角度を $\theta_{a0} = 0,\theta_{a1} = \frac \pi 4, \theta_{b0} = \frac \pi 8, \theta_{b1} = -\frac \pi 8$ と置きます。

パターン 1: $r= 0, s=0$

まずは $r= 0, s=0$ の場合を考えます。このときは $a \oplus b = 0$ で勝利なので、$a= 0, b=0$ か $a=1, b=1$ で勝利になります。

$$
P(\text{win} | r = 0, s=0) = P(a = 0, b=0| r = 0, s=0) + P(a = 1, b=1| r = 0, s=0)
$$

1 つずつ見ていきましょう。$P(a = 0, b=0| r = 0, s=0)$ となる確率は

\begin{aligned}
P(a = 0, b=0| r = 0, s=0) 
&= 
    \left|
        \left\langle
        \phi_0(\theta_{a0}) \otimes \phi_0(\theta_{b0}) | \psi
        \right\rangle
    \right|^2 \\
&= 
    \left|
            (\cos \theta_{a0}\langle 0 | + \sin \theta_{a0}\langle 1 |) \otimes
            (\cos \theta_{b0}\langle 0 | + \sin \theta_{b0}\langle 1 |)  | \psi \rangle
    \right|^2 \\
&=
    \left|
        \begin{pmatrix}
            \cos\theta_{a0}\cos\theta_{b0} & 
            \cos\theta_{a0}\sin\theta_{b0} &
            \sin\theta_{a0}\cos\theta_{b0} & 
            \sin\theta_{a0}\sin\theta_{b0}
        \end{pmatrix}
        \begin{pmatrix}
            \frac 1 {\sqrt 2} \\
            0 \\
            0 \\
            \frac 1 {\sqrt 2}
        \end{pmatrix}
    \right|^2 \\
&=
    \frac 1 2
    \left|
        \cos\theta_{a0}\cos\theta_{b0} + 
        \sin\theta_{a0}\sin\theta_{b0}
    \right|^2 \\
&=
    \frac 1 2
    \left|
        \cos(\theta_{a0} - \theta_{b0})
    \right|^2 \\
&=
    \frac 1 2 \cos^2(\theta_{a0} - \theta_{b0})
\end{aligned}

やっと出ました。$r=0, s= 0$ が与えられた時に $a = 0, b=0$ を提示することで勝利する確率は $\frac 1 2 \cos^2(\theta_{a0} - \theta_{b0})$ であることがわかります。先にも記載したとおり、$r=0, s= 0$ が与えられたときの勝利条件は $a =1, b=1$ の場合もあるので、同様に計算しましょう。

\begin{aligned}
P(a = 1, b=1| r = 0, s=0) 
&= 
    \left|
        \left\langle
        \phi_1(\theta_{a0}) \otimes \phi_1(\theta_{b0}) | \psi
        \right\rangle
    \right|^2 \\
&= 
    \left|
            (-\sin \theta_{a0}\langle 0 | + \cos \theta_{a0}\langle 1 |) \otimes
            (-\sin \theta_{b0}\langle 0 | + \cos \theta_{b0}\langle 1 |)  | \psi \rangle
    \right|^2 \\
&=
    \left|
        \begin{pmatrix}
             \sin\theta_{a0}\sin\theta_{b0} & 
            -\sin\theta_{a0}\cos\theta_{b0} &
            -\cos\theta_{a0}\sin\theta_{b0} & 
             \cos\theta_{a0}\cos\theta_{b0}
        \end{pmatrix}
        \begin{pmatrix}
            \frac 1 {\sqrt 2} \\
            0 \\
            0 \\
            \frac 1 {\sqrt 2}
        \end{pmatrix}
    \right|^2 \\
&=
    \frac 1 2
    \left|
        \cos\theta_{a0}\cos\theta_{b0} + 
        \sin\theta_{a0}\sin\theta_{b0}
    \right|^2 \\
&=
    \frac 1 2
    \left|
        \cos(\theta_{a0} - \theta_{b0})
    \right|^2 \\
&=
    \frac 1 2 \cos^2(\theta_{a0} - \theta_{b0})
\end{aligned}

見て分かる通り、まったく同じ値になりました。まとめると、

\begin{aligned}
P(\text{win} | r = 0, s=0) 
    &= P(a = 0, b=0| r = 0, s=0) + P(a = 1, b=1| r = 0, s=0) \\
    &= \cos^2(\theta_{a0} - \theta_{b0})
\end{aligned}

となることがわかりました。今回は $\theta_{a0} = 0, \theta_{b0} = \frac \pi 8$ なのでだいたい $0.8536$ くらいの確率となります。$r=0, s=0$ であれば、85 % くらいの確率で勝利できることがわかりました。他の場合もどうなるか確かめてみましょう。

パターン 2: $r= 0, s=1$

パターン 1 は長々と計算しましたが、他の場合もやることは同じです。変わるのは基底に含まれた角度 $\theta$ だけなので、もう計算する必要もありませんね。

\begin{aligned}
P(a = 0, b=0| r = 0, s=1) 
&= 
    \left|
        \left\langle
        \phi_0(\theta_{a0}) \otimes \phi_0(\theta_{b1}) | \psi
        \right\rangle
    \right|^2 \\
&=
    \frac 1 2 \cos^2(\theta_{a0} - \theta_{b1})
\end{aligned}

\begin{aligned}
P(a = 1, b=1| r = 0, s=1) 
&= 
    \left|
        \left\langle
        \phi_1(\theta_{a0}) \otimes \phi_1(\theta_{b1}) | \psi
        \right\rangle
    \right|^2 \\
&=
    \frac 1 2 \cos^2(\theta_{a0} - \theta_{b1})
\end{aligned}

なので

\begin{aligned}
P(\text{win} | r = 0, s=1) 
    &= P(a = 0, b=0| r = 0, s=1) + P(a = 1, b=1| r = 0, s=1) \\
    &= \cos^2(\theta_{a0} - \theta_{b1})
\end{aligned}

となります。この場合も 85 % くらいで勝利できます。

パターン 3: $r= 1, s=0$

これも明らかですね。さらに飛ばしましょう。

\begin{aligned}
P(\text{win} | r = 1, s=0) 
    &= P(a = 0, b=0| r = 1, s=0) + P(a = 1, b=1| r = 1, s=0) \\
    &= \cos^2(\theta_{a1} - \theta_{b0})
\end{aligned}

となります。$\theta_{a1}$ が出てきますが、$\cos$ の中身は $\frac \pi 8$で変わりません。なので、これも 85% くらいですね。

パターン 4: $r= 1, s=1$

これも明らかと言いたいところですが、この場合は勝利条件が異なることに注意が必要です。すなわち、これまでは $a, b$ が共に 0 もしくは 1 の場合に勝利だったのですが、今回は $a$ と $b$ がそれぞれ異なる場合が勝利条件となります。順番に見ていきましょう。まずは $a = 0, b=1$ となる確率です。

\begin{aligned}
P(a = 0, b=1| r = 1, s=1) 
&= 
    \left|
        \left\langle
        \phi_0(\theta_{a1}) \otimes \phi_1(\theta_{b1}) | \psi
        \right\rangle
    \right|^2 \\
&= 
    \left|
            ( \cos \theta_{a1}\langle 0 | + \sin \theta_{a1}\langle 1 |) \otimes
            (-\sin \theta_{b1}\langle 0 | + \cos \theta_{b1}\langle 1 |)  | \psi \rangle
    \right|^2 \\
&=
    \left|
        \begin{pmatrix}
            -\cos\theta_{a1}\sin\theta_{b1} & 
             \cos\theta_{a1}\cos\theta_{b1} &
            -\sin\theta_{a1}\sin\theta_{b1} & 
             \sin\theta_{a1}\cos\theta_{b1}
        \end{pmatrix}
        \begin{pmatrix}
            \frac 1 {\sqrt 2} \\
            0 \\
            0 \\
            \frac 1 {\sqrt 2}
        \end{pmatrix}
    \right|^2 \\
&=
    \frac 1 2
    \left|
        \sin\theta_{a1}\cos\theta_{b1} - 
        \cos\theta_{a1}\sin\theta_{b1}
    \right|^2 \\
&=
    \frac 1 2
    \left|
        \sin(\theta_{a1} - \theta_{b1})
    \right|^2 \\
&=
    \frac 1 2 \sin^2(\theta_{a1} - \theta_{b1})
\end{aligned}

今度は $\sin$ になりました。続いて $a = 1, b=0$ となる確率です。

\begin{aligned}
P(a = 1, b=0| r = 1, s=1) 
&= 
    \left|
        \left\langle
        \phi_1(\theta_{a1}) \otimes \phi_0(\theta_{b1}) | \psi
        \right\rangle
    \right|^2 \\
&= 
    \left|
            (-\sin \theta_{a1}\langle 0 | + \cos \theta_{a1}\langle 1 |) \otimes
            ( \cos \theta_{b1}\langle 0 | + \sin \theta_{b1}\langle 1 |)  | \psi \rangle
    \right|^2 \\
&=
    \left|
        \begin{pmatrix}
            -\sin\theta_{a1}\cos\theta_{b1} & 
            -\sin\theta_{a1}\sin\theta_{b1} & 
             \cos\theta_{a1}\cos\theta_{b1} &
             \cos\theta_{a1}\sin\theta_{b1}
        \end{pmatrix}
        \begin{pmatrix}
            \frac 1 {\sqrt 2} \\
            0 \\
            0 \\
            \frac 1 {\sqrt 2}
        \end{pmatrix}
    \right|^2 \\
&=
    \frac 1 2
    \left| -(
        \sin\theta_{a1}\cos\theta_{b1} - 
        \cos\theta_{a1}\sin\theta_{b1}
    ) \right|^2 \\
&=
    \frac 1 2
    \left| -(
        \sin(\theta_{a1} - \theta_{b1})
    ) \right|^2 \\
&=
    \frac 1 2 \sin^2(\theta_{a1} - \theta_{b1})
\end{aligned}

こちらも同じ値となります。まとめると、

\begin{aligned}
P(\text{win} | r = 1, s=1) 
    &= P(a = 0, b=1| r = 1, s=1) + P(a = 1, b=0| r = 1, s=1) \\
    &= \sin^2(\theta_{a1} - \theta_{b1})
\end{aligned}

上記の確率を計算すると、これもまた 85% くらいとなります。

全パターン合わせた勝利確率は？

全部 85 % だったんだから 85 % だろと思われるのは当然かもしれませんが、審判がランダムに $r$ と $s$ を選択する場合、アリスとボブが勝利する確率は

\begin{aligned}
P(\text{win}) 
&= \frac 1 4 
    \left(
        \cos^2(\theta_{a0} - \theta_{b0}) + 
        \cos^2(\theta_{a0} - \theta_{b1}) +
        \cos^2(\theta_{a1} - \theta_{b0}) +
        \sin^2(\theta_{a1} - \theta_{b1})
    \right) \\
&= \frac 1 4
    \left(
        3\cos^2\frac \pi 8 + 
         \sin^2\frac {3\pi} 8
    \right) \\
& \approx 0.85
\end{aligned}

というわけで、アリスとボブは量子コンピュータを利用した先の戦略をとることで、**およそ 85%**の確率で審判に勝利することができることがわかりました。古典アルゴリズムの場合は 75% しか勝利できなかったので、約 10 % 改善されたことになります。やったね！これを高いととるか低いととるかは人の感性によるかもしれませんが、できないことができるというのはいずれにしても価値があるかな、と個人的には思います。

また、意味ありげに 審判がランダムに $r$ と $s$ を選択する と書きましたが、上記の基底を利用する場合は全パターンの勝利確率が同じになるので、確率に偏りがある場合でも勝利確率は変わりません。

というわけで解説を全部済ませたあとになりますが、Task の解説に移ります。

Task 1.1. Win condition

問題

入力: アリスとボブが与えられる値 $x$, $y$ 及びアリスとボブの提示する値 $a$, $b$

出力: アリスとボブが勝利する ($a \oplus b = x \land y$ が成り立つ) なら True を、そうでないなら False を返す。

解説

まんまですね。特に難しくありません。

function WinCondition (x : Bool, y : Bool, a : Bool, b : Bool) : Bool {
    return (x and y) == XOR(a,b);
}

Task 1.2. Alice and Bob's classical strategy

問題

入力: アリスが受け取る値 $x \in \{0, 1\}$ とボブが受け取る値 $y\in \{0, 1\}$

出力: 古典アルゴリズムに基づき、アリスとボブが最適と考えられる値 $a, b\in \{0, 1\}$ を出力する。

解説

まずは古典コンピューターの場合です。先の解説でも記載したとおり、アリスとボブは何も考えずに False を返した場合でも確率 0.75 で勝利することができます。回答は以下となります。

operation AliceClassical (x : Bool) : Bool {
    return false;
}

operation BobClassical (y : Bool) : Bool {
    return false;
}

余談ですが、なんでオペレーションなんでしょうね。。。1.1 と同様、Function でいいじゃんと思ってしまいました。

Task 2.1. Entangled pair

問題

入力: 2つの量子ビット $|00\rangle$

ゴール: ベル状態 $|\phi^+\rangle = (|00\rangle + |11\rangle)/\sqrt 2$ を作る。

解説

続いて量子的な CHSH ゲームに入ります。まずはベル状態の生成ですが、これも楽勝ですね。これまで何度も何度もやってきたとおりです。

operation CreateEntangledPair (qs : Qubit[]) : Unit {
    EqualityFactI(Length(qs), 2, "The array should have exactly 2 qubits.");
    H(qs[0]);
    CNOT(qs[0],qs[1]);
}

Task 2.2. Alice's quantum strategy

問題

入力: アリスが受け取る値 $x$ とボブとの間で量子もつれ状態となっている量子ビット

出力: $x=0$ なら計算基底で、$x=1$ なら X 基底に対して観測を行い、結果を出力する。

解説

タイトル通り、アリスが取る戦略です。問題設定が X 基底で観測せよ、となっているのはなぜでしょうか。若干 Mesurement や Joint Measurement の Kata の復習となりますが、パウリの X 基底

X = \begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}

は明らかに固有値 $\pm 1$ を持ち、それぞれの固有ベクトルは

\begin{aligned}
|\psi_{\lambda = 1} \rangle &= \frac 1 {\sqrt 2}
    \begin{pmatrix}
        1 & 1
    \end{pmatrix}^T \\
|\psi_{\lambda = -1} \rangle &= \frac 1 {\sqrt 2}
    \begin{pmatrix}
        -1 & 1
    \end{pmatrix}^T
\end{aligned}

となり、解説に記載した定義 $|\phi_0(\theta)\rangle, |\phi_1(\theta)\rangle$ で $\theta = \frac \pi 4$ したときと同じになっていることが確認できます。要は、このベクトル対を基底として観測を行うということは、パウリの X 基底で観測を行うことだという事がわかります。回答自体は記載どおりに観測すれば終了なのでとくにつまるところもないのですが、個人的には最初あれっと思いました。というわけで回答は以下となります。

operation AliceQuantum (bit : Bool, qubit : Qubit) : Bool {
    if(bit) {
        return ResultAsBool( Measure([PauliX],[qubit]));
    } else {
        return ResultAsBool( M(qubit));
    }
}

Task 2.3. Rotate Bob's qubit

問題

入力: 回転方向が時計まわりか否かを示す Bool 値と、回転される量子ビット

ゴール: 与えられた量子ビットを Bool 値に従って $\frac \pi 8$ もしくは $-\frac \pi 8$ だけ $Y$ 軸周りに回転せよ。

解説

先程のアリスが $\frac \pi 4$ 回転した基底による観測を行いたい際には X 基底で実現できたのですが、ボブの場合はそんな便利な基底がないので、観測前に自分で回転する必要があります。ただ Ry で回転すれば終了なので、これも特に難しくはないかな、と思います。回答は以下です。

operation RotateBobQubit (clockwise : Bool, qubit : Qubit) : Unit {
    if(clockwise) {
        Ry(-PI()/8.0 * 2.0, qubit);
    } else {
        Ry(PI()/8.0 * 2.0, qubit);
    }
}

Task 2.4. Bob's quantum strategy

問題

入力: ボブが受け取る値 $y$ とアリスとの間で量子もつれ状態となっている量子ビット

出力: $x=0$ なら基底 $|\phi_0(\frac \pi 8)\rangle, |\phi_1(\frac \pi 8)\rangle$ で、$x=1$ なら基底 $|\phi_0(-\frac \pi 8)\rangle, |\phi_1(-\frac \pi 8)\rangle$ で観測を行い、結果を出力する。

解説

先程のタスクで回転する処理をつくったので、あとは回転させてから M オペレーションで計算基底に対する観測を行えば終了ですね。これもタスク自体は難しくないかと思います。回答は以下です。

operation BobQuantum (bit : Bool, qubit : Qubit) : Bool {
    RotateBobQubit(not bit, qubit);
    return ResultAsBool( M(qubit));
}

Task 2.5. Play the CHSH game using the quantum strategy

問題

入力: アリスとボブが量子的な戦略に従って Bool 値を出力するオペレーション askAlice と askBob。アリスとボブは既に質問 $x, y$ を受け取っている。

出力: アリスとボブの回答 $a, b$

解説

正直、よくわかんない問題だなと思いました。今まで Operation を作ってきたのだから、審判から $x, y$ が与えられた際に $a, b$ を出力する全体の Operation を作るものとばかり思っていましたが、この最後の問題はアリスとボブがとる戦略の実装が与えられ、それを呼び出せば終了というものになっています。(実際には、テストから先の Task で作成した AliceQuantum などが呼び出されているので使われてはいるのですが。) そこは自分たちでやるんじゃないんですね、という感じに思えてしまうのは私だけでしょうか。

戦略が与えられるので、あとは呼び出した結果を返してあげれば終了です。これもタスク自体は難しくないですね。

operation PlayQuantumCHSH (askAlice : (Qubit => Bool), askBob : (Qubit => Bool))
        : (Bool, Bool) {
    body(...) {
        mutable result = new Bool[2];
        using(qs = Qubit[2]) {
            CreateEntangledPair(qs);
            set result w/= 0 <- askAlice(qs[0]);
            set result w/= 1 <- askBob(qs[1]);
            ResetAll(qs);
        }
        return (result[0], result[1]);
    }

}

配列に結果を代入する際には、QDK 0.6 でサポートされた copy-and-update-expressions を利用してみました。

まとめ

この記事では、CHSH ゲームとゲームの実装である Kata について解説しました。タスクや実装自体は難しくないものの、概念やアプローチがこれまでの Kata で学んだ量子アルゴリズムとは一線を画す内容であり、新鮮だなと感じました。そして、Quantum Katas をやっているだけで量子情報のあらゆる分野の勉強ができるなんて、本当に素敵な教材ですね。

次回は GHZ ゲームをまとめる予定です。