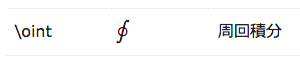注意:これは下記を引用した私的メモです。
Qiitaの数式チートシート
QiitaではMathJaxというライブラリを使っていて、ブラウザ上で美しい数式を見ることができます。
MathJaxにおける数式の記述方法はTeX記法に則っています。
以下Qiitaにおける数式を書くためのチートシートです。
数式の記述方法
コードブロックの言語指定に math を指定することでTeX記法を用いて数式を記述することができます。
```math
e^{i\pi} = -1
```
e^{i\pi} = -1
また、$$で囲むことで独立した段落として記述することもできます。
$$ e^{i\theta} = \cos\theta + i\sin\theta $$
$$ e^{i\theta} = \cos\theta + i\sin\theta $$
その他にも数式を$で囲むことで埋め込み形式として記述できます
$ e^{\pi i}= -1 $はオイラーの等式として知られています
$ e^{\pi i}= -1 $はオイラーの等式として知られています
改行(\\)
数式の行末に\\(バックスラッシュ2つ)をつけることによって改行をすることができます。
四則演算
```math
1 + 2 = 3 \
2 - 3 = 5 \
3 \times 2 = 6 \
6 \div 3 = 2
```
1 + 2 = 3 \\
2 - 3 = 5 \\
3 \times 2 = 6 \\
6 \div 3 = 2
分数
```math
\frac{1}{2} - \frac{1}{3} = \frac{1}{6} \
\frac{a+b}{2ab}
```
\frac{1}{2} - \frac{1}{3} = \frac{1}{6} \\
\frac{a+b}{2ab}
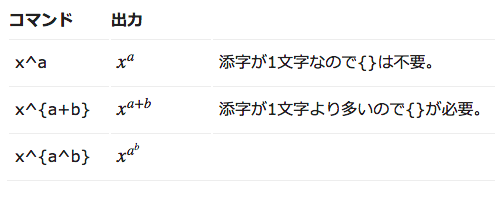
上付き・下付き文字
上付き文字
```math
ax^2 + bx + c = 0 \
y = x^{\frac{1}{2}}
```
ax^2 + bx + c = 0 \\
y = x^{\frac{1}{2}}
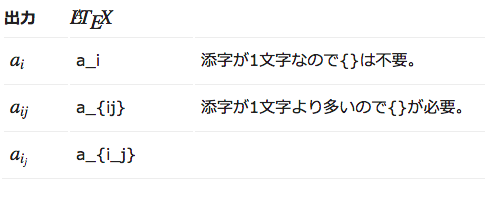
下付き文字
```math
x_{n+1} = rx_n(1-x_n)
```
x_{n+1} = rx_n(1-x_n)
イコール(=)を揃える
begin{align}とend{align}と&を用いることによってブロック内で改行前後の位置を揃える
```math
\begin{align}
f(x) &= x^2+3x+2 \
&= (x+1)(x+2)
\end{align}
```
\begin{align}
f(x) &= x^2+3x+2 \\
&= (x+1)(x+2)
\end{align}
文字の間隔
一般的なスペース
```math
y \quad = ax \qquad + b
```
y \quad = ax \qquad + b
調整可能なスペース
```math
a \hspace{50pt} b \hspace{1cm} c
```
a \hspace{50pt} b \hspace{1cm} c
小さなスペース
```math
a ! b , c : d ; e \
a !! b ,, c :: d ;; e
```
a \! b \, c \: d \; e \\
a \!\! b \,\, c \:\: d \;\; e
括弧の大きさ
下に行くほど括弧が大きくなる
左括弧
\bigl
\Bigl
\biggl
\Biggl
右括弧
\bigr
\Bigr
\biggr
\Biggr
丸括弧()・角括弧[]・波括弧{}を使いたいときは、それぞれの括弧の後ろにつける
```math
a \Biggl(
b \biggl(
c \Bigl(
d \bigl(
e ( f + g )
\bigr)
\Bigr)
\biggr)
\Biggr)
```
a \Biggl(
b \biggl(
c \Bigl(
d \bigl(
e ( f + g )
\bigr)
\Bigr)
\biggr)
\Biggr)
極限(lim)
```math
\lim_{x \to \infty} f(x) \
\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \
\lim_{\substack{x \to \infty \ y \to \infty}} f(x,y)
```
\lim_{x \to \infty} f(x) \\
\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\
\lim_{\substack{x \to \infty \\ y \to \infty}} f(x,y)
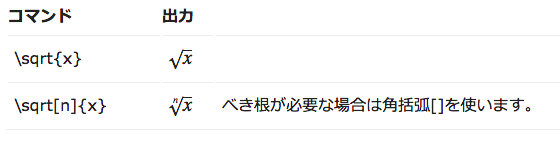
平方根(sqrt)
```math
\sqrt{a^2+b^2} \
\sqrt[3]{a}
```
\sqrt{a^2+b^2} \\
\sqrt[3]{a}
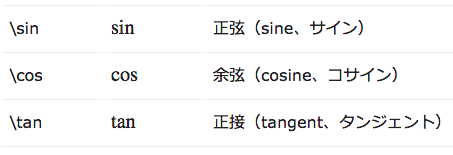
三角関数(sin, cos, tan)
```math
\sin^2 x + \cos^2 x = 1
```
\sin^2 x + \cos^2 x = 1
指数関数(e, exp)
```math
e^{i\pi} = -1 \
e^{i\theta} = \cos \theta + i \sin \theta
```
e^{i\pi} = -1 \\
e^{i\theta} = \cos \theta + i \sin \theta
対数関数・自然対数(log, ln)
```math
\log_a \frac{x}{y} = \log_a x - \log_a y \
\ln \frac{x}{y}
```
\log_a \frac{x}{y} = \log_a x - \log_a y \\
\ln \frac{x}{y}
積分・重積分・周回積分(∫)
積分
```math
\int f(x)dx \
\int_{a}^{b}f(x)dx
```
\int f(x)dx \\\
\int_{a}^{b}f(x)dx
重積分
```math
\iint f(x,y)dxdy
```
\iint f(x,y)dxdy
周回積分
```math
\oint_C \frac{1}{z}dz
```
\oint_C \frac{1}{z}dz
和・総和(シグマΣ)
```math
\sum_{k=1}^{n} k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} \
\sum_{k=1}^{n} k^2 = 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}
```
\sum_{k=1}^{n} k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} \\
\sum_{k=1}^{n} k^2 = 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}
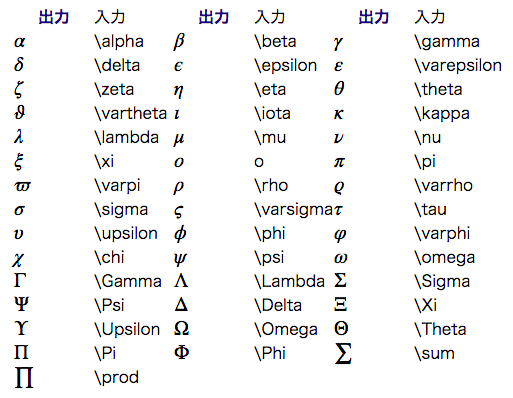
ギリシャ文字
```math
i \hbar \frac{\partial \psi}{\partial t} = H \psi(x,t)
```
i \hbar \frac{\partial \psi}{\partial t} = H \psi(x,t)
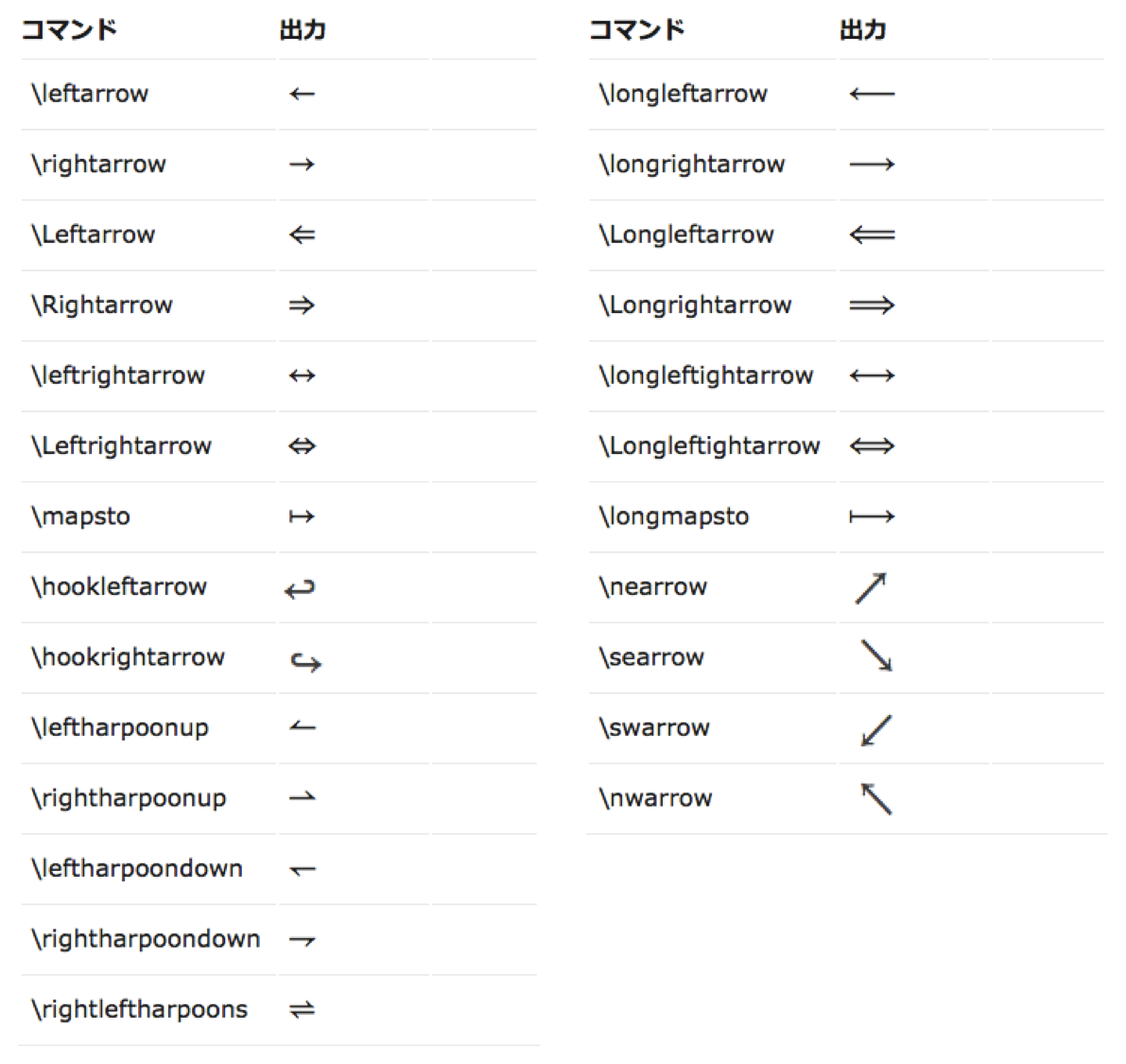
等号、不等号、演算子、集合
矢印記号
```math
\begin{align}
\qquad &ax^2+bx+c = 0 \
\Leftrightarrow &\quad x^2 + \frac{b}{a}x = - \frac{c}{a} \
\Leftrightarrow &\quad x^2 + \frac{b}{2a} x + \frac{b^2}{4a^2} = \frac{b^2}{4a^2} - \frac{c}{a} \
\Leftrightarrow &\quad (x + \frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2} \
\Leftrightarrow &\quad x + \frac{b}{2a} = \pm \frac{\sqrt{b^2-4ac}}{2a} \
\therefore &x = \frac{-b \pm \sqrt{b^2-4ac} }{2a}
\end{align}
```
\begin{align}
\qquad &ax^2+bx+c = 0 \\
\Leftrightarrow &\quad x^2 + \frac{b}{a}x = - \frac{c}{a} \\
\Leftrightarrow &\quad x^2 + \frac{b}{2a} x + \frac{b^2}{4a^2} = \frac{b^2}{4a^2} - \frac{c}{a} \\
\Leftrightarrow &\quad (x + \frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2} \\
\Leftrightarrow &\quad x + \frac{b}{2a} = \pm \frac{\sqrt{b^2-4ac}}{2a} \\
\therefore &x = \frac{-b \pm \sqrt{b^2-4ac} }{2a}
\end{align}
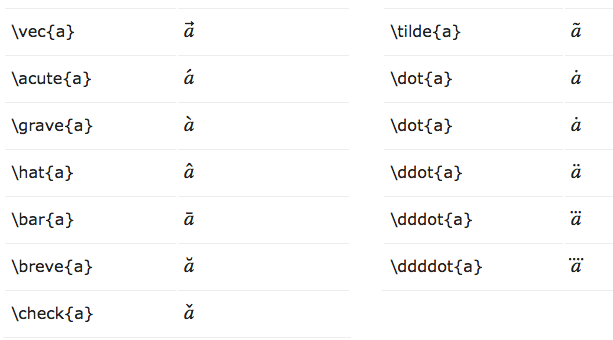
アクセント記号(ベクトルなど)
```math
\vec{A} = \vec{B} + \vec{C} \
F = m\ddot{x}
```
\vec{A} = \vec{B} + \vec{C} \\
F = m\ddot{x}
ドット(3点リーダー)
```math
\left(
\begin{array}{ccccc}
a_{11} & \cdots & a_{1i} & \cdots & a_{1n}\
\vdots & \ddots & & & \vdots \
a_{i1} & & a_{ii} & & a_{in} \
\vdots & & & \ddots & \vdots \
a_{n1} & \cdots & a_{ni} & \cdots & a_{nn}
\end{array}
\right)
```
\left(
\begin{array}{ccccc}
a_{11} & \cdots & a_{1i} & \cdots & a_{1n}\\
\vdots & \ddots & & & \vdots \\
a_{i1} & & a_{ii} & & a_{in} \\
\vdots & & & \ddots & \vdots \\
a_{n1} & \cdots & a_{ni} & \cdots & a_{nn}
\end{array}
\right)
行列と行列式
```math
\begin{matrix}
a & b \
c & d
\end{matrix}
```
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
```math
\begin{pmatrix}
a & b \
c & d
\end{pmatrix}
```
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
```math
\begin{bmatrix}
a & b \
c & d
\end{bmatrix}
```
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix}
```math
\begin{vmatrix}
a & b \
c & d
\end{vmatrix}
```
\begin{Vmatrix}
a & b \\
c & d
\end{Vmatrix}
```math
\begin{pmatrix}
a & b \
c & d
\end{pmatrix}
\times
\begin{vmatrix}
e & f \
g & h
\end{vmatrix}
```
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\times
\begin{vmatrix}
e & f \\
g & h
\end{vmatrix}
場合分け
```math
f(x) = \left\{
\begin{array}{ll}
1 & (x \geq 0) \
0 & (x \lt 0)
\end{array}
\right.
```
f(x) = \left\{
\begin{array}{ll}
1 & (x \geq 0)\\
0 & (x \lt 0)
\end{array}
\right.