はじめに
統計検定2級の範囲で勉強したことを簡単にですがまとめてみました。すべてを網羅しているわけではないので参考程度に活用していただければと思います。
分散・期待値・相関係数
E[X+Y] = E[X] + E[Y]\\
E[X-Y] = E[X] - E[Y]\\
E[aX+b] = aE[X]+b\\
分散は係数の2乗倍\\
V[aX+b] = a^2V[X]\\
V[X+Y] = V[X]+V[Y]+2Cov[X,Y]\\
V[X-Y] = V[X]+V[Y]-2Cov[X,Y]\\
X,Yが独立、または無相関だと\\
V[X+Y] = V[X]+V[Y]\\
V[X-Y] = V[X]+V[Y]\\
V[X] = E[X^2] - {E[X]}^2\\
r = \frac{Cov[X,Y]}{\sqrt{V[X]V[Y]}}
共分散
Cov[X+Y, Z] = Cov[X,Z]+Cov[Y,Z]\\
Cov[aX,Y]= aCov[X,Y]\\
Cov[X,Y] = E[XY]-E[X]E[Y]\\
Cov[X+Y,X-Y]=Cov[X,X]- Cov[X,Y]+Cov[X,Y]-Cov[Y,Y]\\
共分散・相関係数
- 2種類のデータに対し、片方のデータの値に定数を足しても共分散・相関係数は変わらない
- 両方のデータに定数を足しても共分散・相関係数は変わらない
- 片方のデータをa倍すると、共分散はa倍され、相関係数は $ \frac{a}{|a|} $ 倍
- 両方のデータをa倍すると、共分散は$a^2$倍、相関係数は変わらない
標本平均の分散
V[\bar{X}] = V[\frac{1}{n} \sum_{i=1}^n X_i]\\
= \frac{1}{n^2}V[\sum_{i=1}^n X_i]\\
= \frac{1}{n^2} \sum_{i=1}^n \sigma^2 \\
= \frac{1}{n^2}(n\sigma^2)\\
= \frac{\sigma^2}{n}\\
ベルヌーイ試行(1回の試行)
試行結果が「○か☓」や「成功か失敗」のように2種類しかない試行を、ベルヌーイ試行という。
E[X] = p \\
V[X] = p(1-p) = pq \\
二項分布(n回の試行)
「互いに独立したベルヌーイ試行をn回行った時にある事象が何回起こるかの確率分布」のことを二項分布という
$ B(n, p)$ で表される。
P(X = k) = {}_{n} C _{k}p^k(1-p)^{n-k}\\
E[X] = np \\
V[X] = np(1-p) \\
nがある程度大きいときは、中心極限定理によって、$B(n, p)$ は正規分布$N(np, np(1-p))$ に近似できる。これによってXが二項分布$B(n,p)$に従う場合、Xを標準化した値はnが十分に大きいときにはZは標準正規分布$N(0,1)$ に従う。
Z = \frac{X - np}{np(1-p)} \\
また、標本比率$\hat{p}$は、 $\hat{p} = \frac{X}{n}$ から求められる。よって
Z = \frac{X - np}{\sqrt{np(1-p)}} = \frac{\frac{X}{n}-p}{\sqrt\frac{\hat{p}(1-p)}{n}} \\
となり、次の式もnが十分に大きいとき標準正規分布$N(0,1)$に従う。また、$\hat{p}$は近似的に正規分布$N(p, \frac{p(1-p)}{n})$に従う。
パラメータpの推定量 $\bar{Y_n} = \frac{Y_n}{n}$の分散は、
V[Y_n] = \frac{p(1-p)}{n} \\
となり、分散を最大にするのは確率が50%のときである。
ポアソン分布(まれな試行)
ある期間に平均$λ$回起こる現象が$k$回起こる確率.
ある期間に起こる回数に関する分布。
P(X = k) = \frac{e^{-λ}λ^k}{k!} \\
\\
E[X] = λ \\
V[X] = λ \\
λ = np \\
幾何分布
成功確率がpである独立なベルヌーイ試行を繰り返すとき、初めて成功するまでの試行回数Xが従う確率分布。
離散的待ち時間分布とも言われる。
無記憶性:ある事象が発生する確率は、その事象が発生する前の情報の影響を受けない
P(X = k) = (1 - p)^{k-1}p \\
E[X] = \frac{1}{p} \\
V[X] = \frac{1-p}{p^2} \\
[例]
サイコロを投げて1が出る確率は、$\frac{1}{6}$, 3投目で初めて1が出る確率。
P(X = 3) = (1 - \frac{1}{6})^{3 - 1}* \frac{1}{6} = 0.116 \\
指数分布
機械が故障してから次に故障するまでの期間のように、次に何かが起こるまでの期間が従う分布。ある期間に平均して$λ$回起こる現象が、次に起こるまでの期間Xが指数分布に従うとき、X=xとなる確率密度関数はつぎの式になる。
f(x) = λe^{-λx} (x>0) \\
E[X] = \frac{1}{λ} \\
V[X] = \frac{1}{λ^2} \\
ある期間に平均してλ回起こる現象が次に起こるまでの期間をXとしたとき、「期間Xがx以下となる確率」、すなわち「xまでの累積分布関数F(x)」はつぎのようになる。
F(x) = P(X<=x)=1 - e^{-λx} \\
標本の抽出法
1. 単純無作為抽出法
母集団の要素から、どの要素も同じ確率となるよう無作為に抽出
+)理論的に単純であり、誤差の計算が楽
-)母集団を見るリストが必要
2.クラスター(集団)抽出法
母集団を分割してクラスターを作った上で複数のクラスターを抽出して、抽出されたクラスターの要素についてはすべて調査する。
+)単純無作為抽出法よりコストが少ない
-)単純無作為抽出と比べて精度は落ちる傾向がある
3.多段抽出法
クラスター抽出して抽出した集団から無作為に抽出
+) 抽出のコスト減少
-) 段数が増えるほど推定の精度が落ち、偏りが生じやすい(調査するものが少なくなるから)
-) 局所的なところしか反映できていない
4. 層別(層化)抽出法
母集団に関する補足情報を活かして、母集団をできるだけ均質な構成要素から構成される層に分割して各層から標本を抽出することで精度を上げようとする方法。母集団をあらかじめいくつかの層(グループ)に分けておき、各層の中から必要な数の調査対象を無作為に抽出する方法とも言える。
+) 単純無作為抽出法よりも精度は高い
-)層を構成する比率について事前情報が必要
5.系統抽出法(等間隔抽出法)
要素全てに番号を振り、1つ目の要素は無作為に抽出し、2つ目以降は等間隔の番号で抽出。規則性をもって抽出するイメージ。
+)抽出がかんたんで間違いが少ない
+)母分散全体に散らばらせることができる
-)母集団の並び方に規則性があると精度が落ちる
価格に関する指標
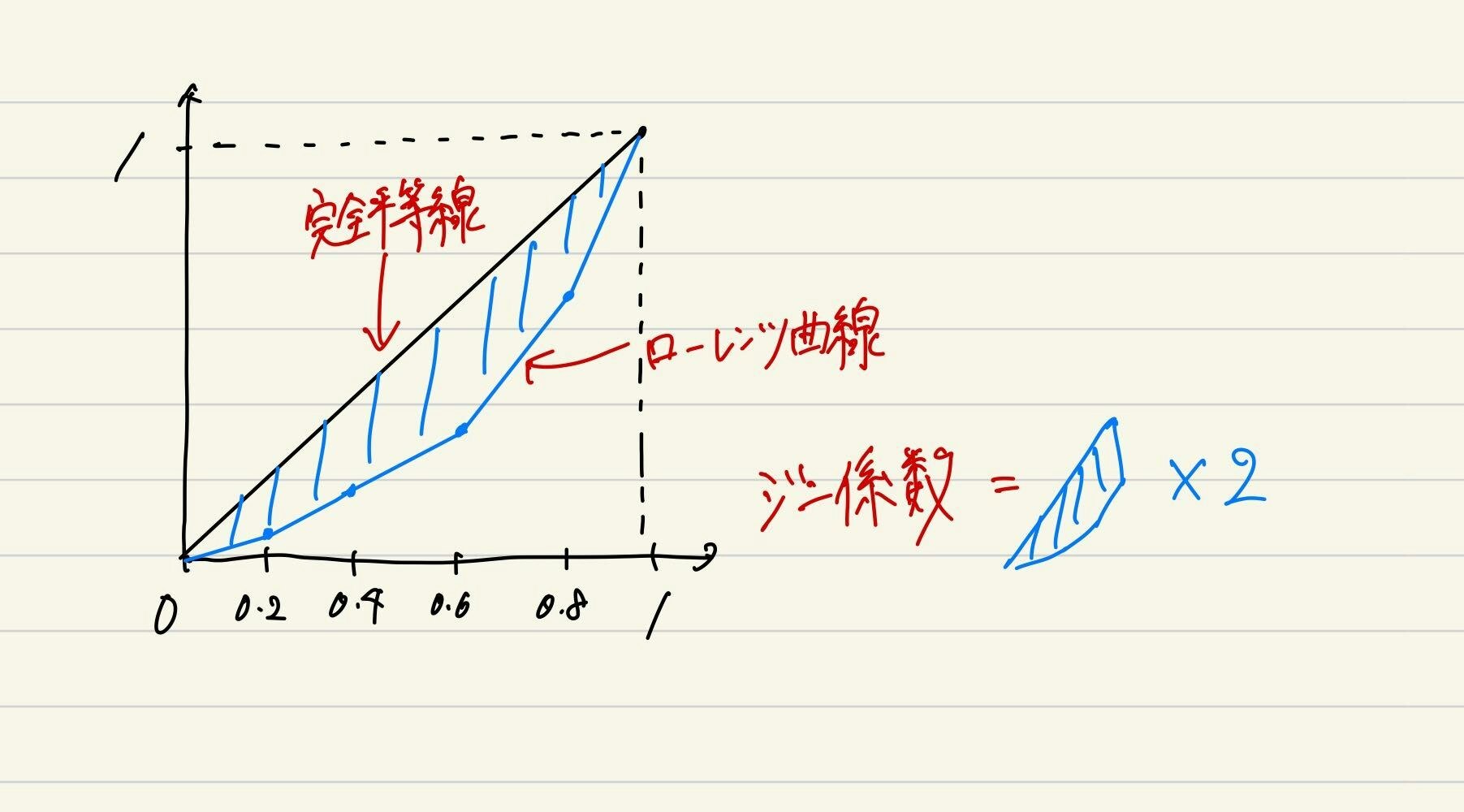
1. ローレンツ曲線
分布を持つような事象がどの程度あるか。
ジニ係数 -- ローレンツ曲線と完全平等線の間の面積の2倍
ジニ係数は0-1の間を取り、0だと偏りがない。1に近いと偏りが生じている。
2.ラスパイレス指数
物価の変動を表す時によく使われる
基準年の購入量や取引量等を重みとして算出した価格指数
\ P_L = \frac{\sum_{} P_t * Q_0}{\sum_{} P_0 *Q_0}
$ {P_0} $: 基準年の価格, $ {Q_0} $: 基準年の数量,
$ {P_t} $: 比較年の価格, $ {Q_t} $: 比較年の数量,
3.パーシェ指数
比較年の購入量や取引量を重みとして算出した価格指数のこと
\ P_P = \frac{\sum_{} P_t * Q_t}{\sum_{} P_0 *Q_t}
4.フィッシャー指数
ラスパイレス指数とパーシェ指数の幾何平均によって算出
\sqrt{P_L*P_P}
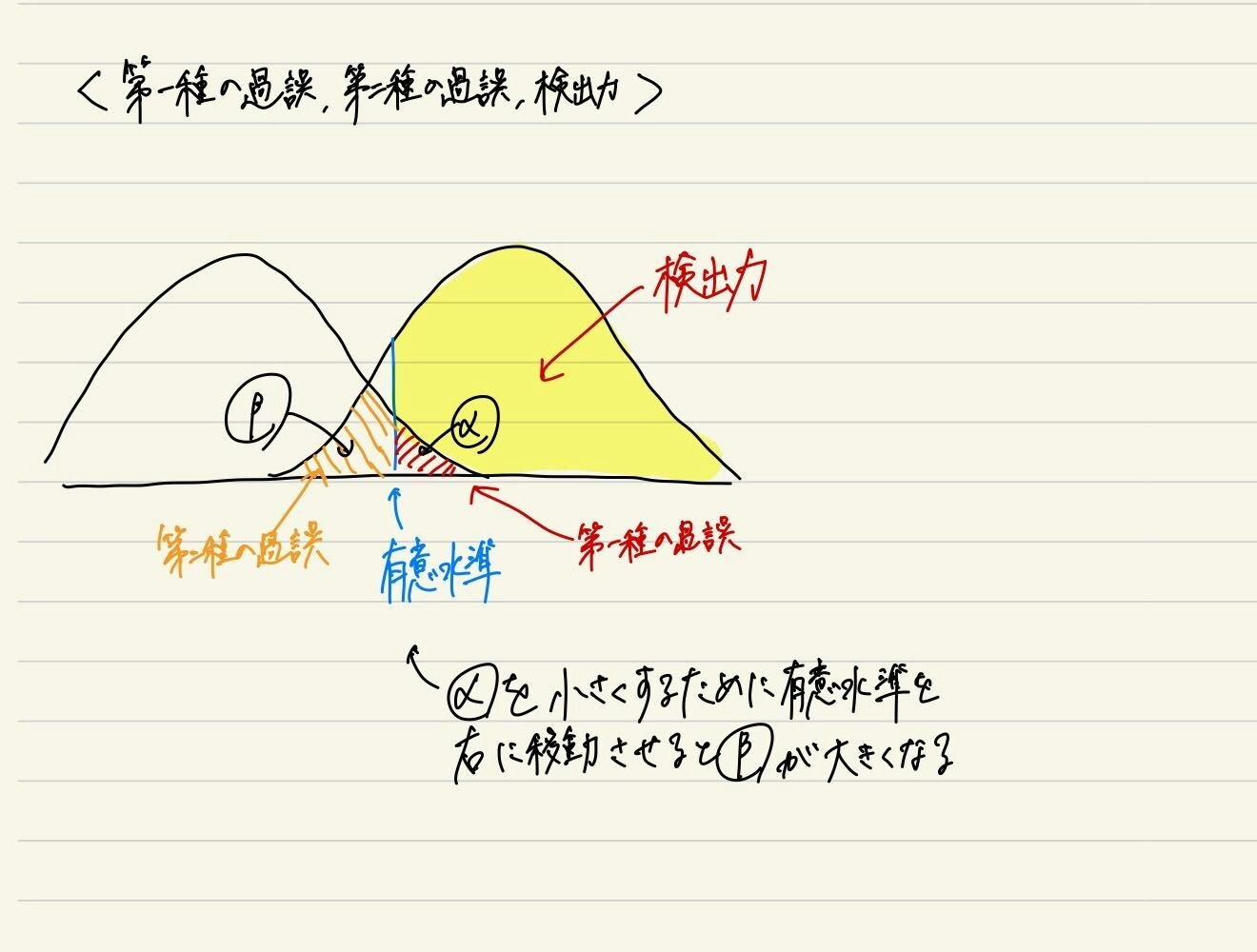
判定
第一種の過誤 : 帰無仮説が真であるのに帰無仮説を棄却する
第二種の過誤 : 対立仮説が真であるのに帰無仮説を棄却しない
検出力 : 対立が真のとき、帰無仮説を正しく棄却する確率
用語
フィッシャーの3原則
目的は、誤差(偶然誤差、系統誤差)を小さくすること。
-
反復(繰り返し)
1回の実験だけだと誤差がどの程度の大きさかわからない
偶然誤差を評価できる -
無作為化
実験を行うときは、位置や順番によって実験者が気がついていない何らかの影響があるかもしれない。系統誤差(ある一定の傾向がある誤差)の影響は小さくする。水準以外の系統誤差を偶然誤差に転化させるために用いる。 -
局所管理
ブロック内でのバックグランドとなる条件を極力同じようにする。局所管理を行うことができれば「無作為化」以上に系統誤差を小さくできる。一部の系統誤差をブロック間変動として除去するために用いる。
誤差論
絶対誤差 = 測定値 - 真値
相対誤差 = 誤差 / 真値
誤差は大きく2つに分けることができる
①系統誤差
- 毎回同じ値
- 測定者の癖や機械固有の特性
- 平均値をずらす形で影響を与える
- 誤差の存在に気づくのが困難
- 誤差の原因がわかれば取り除くことが可能
➁偶然誤差
- 毎回異なる値
- あとから理論的に補正できない
- 測定値のばらつきとして目に見える形で現れる。発見が容易
決定係数
- 回帰によって導いたモデルの当てはまりの良さを表現する値で、モデルによって予測した値が実際の値とどの程度一致しているか表現
- 説明変数がどのくらい目的変数を説明できているか。
- 0-1の範囲、値が大きいほどモデルが適切にデータを表現できている
自由度調整済み決定係数
- $R^2$ が説明変数の数が多くなるにつれて大きくなる(1に近づく)という欠点を補うためのもの
- 説明変数の数の影響を取り除き、見かけ上の当てはまりの良さを差し引いた
- 重回帰式の当てはまりの良さ
F-statistic
帰無仮説 : 「切片を除く、すべての係数が0である」
対立仮説 : 「切片を除く、少なくとも1つの係数は0でない」
偏相関係数
2つの変数の相関が第3の変数によって高められる、または低められる場合に、2変数から第3の変数の影響を取り除いて求めた相関係数。
歪度
分布の非対称性を表現
\frac{E[(x-μ)^3]}{\sigma^3}
尖度
分布の尖度と裾の長さを表す指標
- 正規分布の歪度と尖度が0であることを利用し、正規分布からの離れ具合を評価できる
- 一様分布は左右対称で裾が短い分布なので、歪度=0, 尖度<0 と予想がつく
- t分布は左右対称で裾が長い分布なので、歪度=0, 尖度>0
- 自由度が大きくなると正規分布に近づくことから、自由度が大きいほど尖度の値は小さくなる
\frac{E[(x-μ)^4]}{\sigma^4} -3
変動係数
変動係数 = 標準偏差/平均値
中心極限定理
標本を抽出する母集団が平均 $μ$、分散 $σ^2$の正規分布に従う場合でも従わない場合でも抽出するサンプルサイズnが大きくなるにつれて標本平均の分布は正規分布 $ N(μ, \frac{σ^2}{n})$ に近づく。
大数の法則
母平均が$μ$である集団から標本を抽出する場合、サンプルサイズが大きくなるにつれて標本平均は母平均$μ$に近づく
疑似相関
データの見かけ上は相関関係があっても、実は関係ないもの
回帰分析、t値
t = \frac{傾きの推定値(偏回帰係数)}{標準誤差}
##分布について
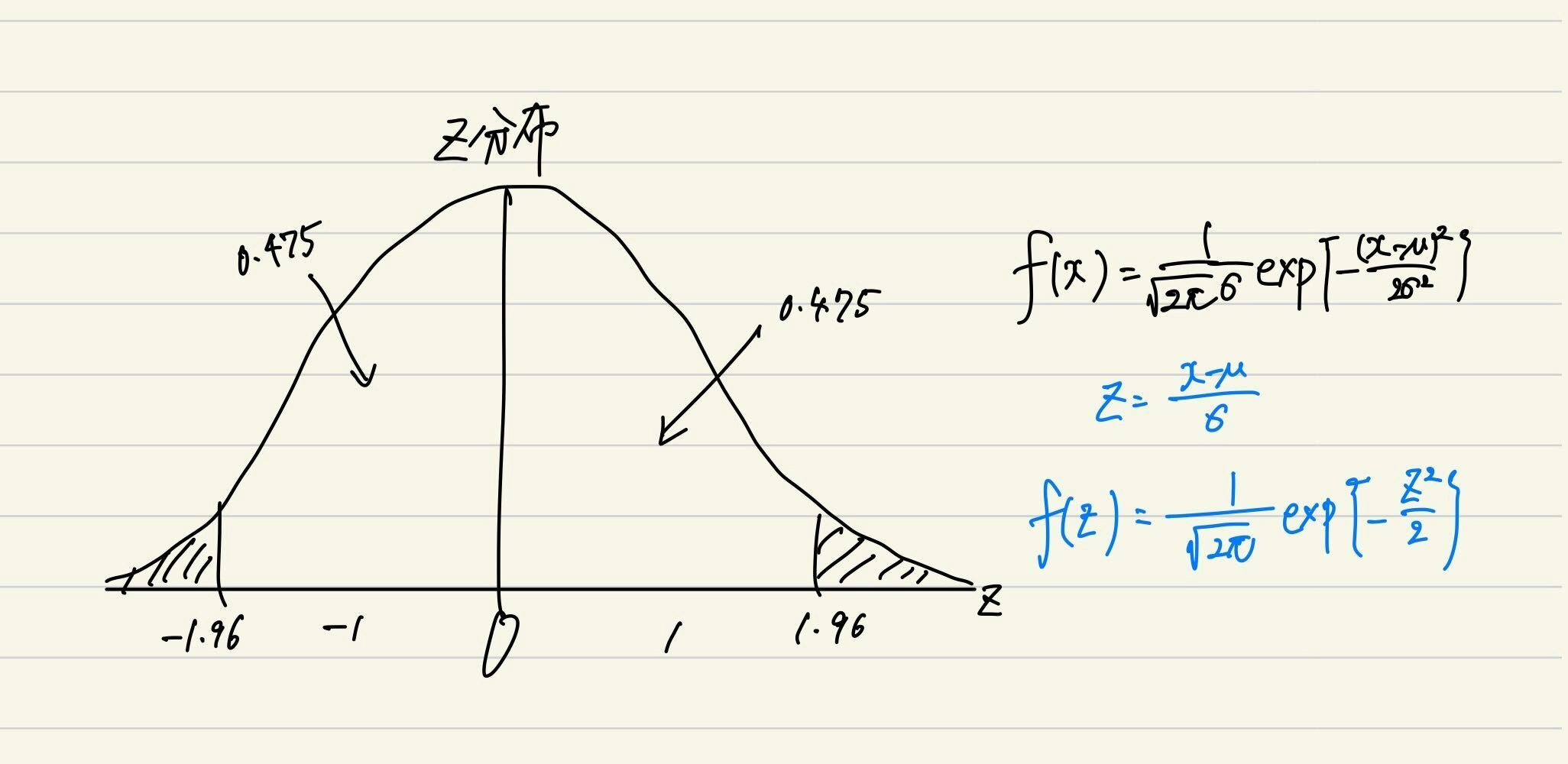
####[1].Z分布(標準正規分布)
正規分布を標準化する
平均0、分散1, N(0,1)
N(μ,σ^2)をN(0,1)のz分布に変換することによって、どのような確率事象に対しても確率分布表を使用し、簡単に正規分布の確率が求められる。
Z分布表は、特定のZから∞までの確率、つまりf(z)の全面積に占める割合を示している
z検定の棄却限界値
| z | S(z) | 1-2S(z) |
|---|---|---|
| 1.64 | 0.050503≒0.05 | 0.90 |
| 1.94 | 0.024998≒0.025 | 0.95 |
| 2.58 | 0.004940≒0.005 | 0.99 |
[使用場面]
- 母分散が既知のときや、未知でも大標本のときの母平均の推定や検定
- 母比率の検定や推定
[2].t分布
z分布と同じで平均は0だが、その形状は、自由度fが小さいとz分布に比べて広がりが大きく、自由度fが大きくなるにしたがってz分布に近づき、自由度が∞のときz分布と一致する。
- 主にサンプル数が小さく、σが未知のときに用いられる。
- 自由度f(n-1)
- 間推定のときは同じ信頼度では、z分布よりt分布のほうが信頼区間が広くなります
[3].カイ二乗分布
カイ二乗分布は、$ Z_1, Z_2, ,,, , Z_k $ が互いに独立で標準正規分布 $ N(0,1)$ に従う、確率変数であるときに、自由度kのカイ二乗が従う確率分布である。
χ^2 = Z_1^2 + Z_2^2 + ・・・ + Z_k^2
- 主に、➀母分散の検定や推定、➁適合度や➂独立性の検定に用いられる
- 上側確率が小さくなるほど $ χ^2$ 値は大きくなります
[4].F分布
- 母分散の比の検定や推定
- F値は1以上なので、数値の大きい方は分子にする
仮説検定
母集団について設定した仮説の採否を、誤差を含んだ標本の結果をもとに、一定の確率水準で判定すること。
帰無仮説 :あらかじめ棄却(reject)されることを目的としている
対立仮説 : 帰無仮説を棄却して、目的とする命題が採択されることを前提
*帰無仮説は棄却することはできるが、帰無仮説が正しいことを証明することはできない
有意水準 : 仮説が正しいときに、検定統計量Tが棄却域内に入る確率。
「有意である」とは、調査結果には通常起こりそうにない異常が認められ、帰無仮説は偽であるとして否定して良いことを意味している
<両側検定をする場合>
①分析者が両側の偏りに関心がある場合
➁調査結果の方向性が想定できない
➂具体的に「AとBに違いがあるか」問われているとき
<片側検定をする場合>
①分析者が特定の方向に関心がある場合
➁具体的に「AはBより大きいか」、「AはBより小さいか」問われているとき
*質問に特別な指定がない場合、両側検定をしておくのがよい
→両側検定のほうが帰無仮説が棄却域に落ちる確率が低くなり、棄却されにくくなるから
標準化したデータの使い方
ある確率変数Xが平均μ、分散σ^2の正規分布に従うとき、Xから平均μを引いて標準偏差σで割った値をzとおくと、zは**「平均0、分散1の標準正規分布」**に従う。
標準化を行うことで、単位や平均値が異なるデータ同士を単純に比較可能
回帰
推定された直線回帰式がどの程度現実のデータに適合しているかを調べる
y_i = a + bx_i+e_i,\\
e_i ~ N(0, \sigma^2)\\
$e_i$ は誤差、残差で、直線回帰式で説明がつかない部分を表す
誤差の大きさが大きいときは、直線回帰式ではデータが説明できないと考える。
回帰で説明がつかない残差平方和$S_e$は、
S_e = \sum_{i} (y_i - y)^2 = \sum_{i}(y_i-a-bx_i)^2
で求められる。これの自由度はn-2(2つの回帰係数分の自由度を除く)であるので、回帰の残差の分散は
se^2 = \frac{S_e}{n-2}
と表現できる。
検定・推定
検定 : パラメトリック検定
(1)母平均の比較値との差のz検定
母平均と比較値が異なるかどうか
\ T = \frac{\bar{x}-μ_0}{\frac{\sigma}{\sqrt{n}}}
- σが既知、または
- σが不明でも大標本
- z分布、大標本(n>=100)
(2)母平均の比較値との差のt検定
母平均と比較値が異なるかどうか
\ T = \frac{\bar{x}-μ_0}{\frac{s}{\sqrt{n}}}
- t分布(自由度=n-1)、σが不明で小標本(n<100)
(3)2つの母平均の差のz検定(対応のないデータ)
標本平均の差をもとに、2つの母平均の差の検定
\ T = \frac{\bar{x_1}-\bar{x_2}}{\sqrt{ \frac{ \sigma_1^2}{n_1} + \frac{ \sigma_2^2}{n_2} }}
- σが既知、または、
- σが不明でも大標本(n1 + n2 >= 100)
(4)2つの母平均の差のt検定(対応のないデータ)
標本平均の差をもとに、2つの母平均の差の検定
\ T = \frac{\bar{x_1}-\bar{x_2}}{\sqrt{ \frac{1}{n_1} + \frac{1}{n_2}} \sqrt{\frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1 + n_2 - 2}}}
- 小標本(n1 + n2 < 100)かつ
- 等分散(母分散の比のF検定)
- 自由度 $ f = n_1 + n_2 -2 $
(5)2つの母平均の差のz検定(対応のあるデータ)
対応のあるデータの差をもとに、2つの母平均に差があるかどうか判定
T = \frac{\bar{d}}{\frac{s_d}{\sqrt{n}}}
- z分布、大標本(n>100)
(6)2つの母平均の差のt検定(対応のあるデータ)
対応のあるデータの差をもとに、2つの母平均に差があるかどうか判定
T = \frac{\bar{d}}{\frac{s_d}{\sqrt{n}}}
- t分布、小標本(n<100)
(7) 母分散の比較値との差のχ二乗検定
カイ二乗分布を活用して、標本分散があらかじめ与えられた比較値と異なるかどうか判定
T = \frac{(n-1)s^2}{\sigma_0^2},
s^2 : 標本分散
\sigma_0^2 : 比較値
- 自由度 f = n-1
(8) 母分散の比のF検定
母分散が異なるかどうか
T = \frac{s_A^2}{s_B^2}
- F分布表の数値が「1」以上の場合、小さい方を分子へ
(9)ピアソンの積率相関係数の無相関のt検定
母相関係数がゼロであるかどうか
\ T = \frac{|r| \sqrt{n - 2}}{\sqrt{1 - r^2}}
- 自由度 $ f = n - 2$ のt分布
検定 : ノンパラメトリック検定
[1]母比率の比較値との差の検定
母比率と比較値が異なるかどうか判定
T = \frac {p - P_0}{ \sqrt{ \frac{ P_0(1-P_0)}{n}}}
- 大標本(n>=30)の時、z分布を活用
[2]2つの母比率の差のz検定(対応のないデータ)
標本比率を差をもとに2つの母比率の差を判定
\ T = \frac {p_1 - p_2}{ \sqrt{ (\frac{1}{n_1} + \frac{1}{n_2})p(1-p)}}\\
\ p = \frac{n_1p_1+n_2p_2}{n_1+n_2}
統合比率を使用する理由
- z検定は正規近似を行っているため、標本サイズが小さいと適切な結果が得られないから
適合度の検定
事象の分布を仮定している
自由度 f = 列数-1のカイ二乗分布
T = \sum_{}\frac{(観測値-期待度数)^2}{期待度数}
独立性の検定
各セルの生起確率が独立な事象の積に分解できると仮定
自由度 = (列数-1) x (行数-1)
T = \sum_{}\frac{(観測値-期待度数)^2}{期待度数}
推定
####[1] 母平均のz推定
標本平均から母平均を推定
\ μ 〜 \bar{x} ±z(α/2) \frac{\sigma}{\sqrt{n}}
- σが既知、または
- σが不明でも大標本(n>=100)
[2] 母平均のt推定
標本平均から母平均を推定
\ μ 〜 \bar{x} ±t(n-1,α/2) \frac{s}{\sqrt{n}}
- σが不明で小標本(<100)
[3] 2つの母平均の差のz推定
\ (μ_1 - μ_2) 〜 (\bar{x_1} - \bar{x_2}) ±z(α/2) \sqrt{ \frac{ \sigma_1^2}{n_1} + \frac{ \sigma_2^2}{n_2} }
- 分散が既知
- 分散が不明でも大標本(n>=100)
[4] 2つの母平均の差のt推定
\ (μ_1 - μ_2) 〜 (\bar{x_1} - \bar{x_2}) ±t(n_1 + n_2 - 2, α/2)\sqrt{ (\frac{1}{n_1} + \frac{1}{n_2} ) \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1 + n_2 - 2} }
- 分散が不明で小標本(n < 100)
[5] 母分散のカイ二乗推定
\frac{S}{χ_{α/2}^2(n-1,α)} <= σ^2 <= \frac{S}{χ_{α/2}^2(n-1,1-α)}
$S$ : 偏差平方和, $S = (n-1)s^2$
- 自由度n-1のカイ二乗分布に従うことを用いて信頼区間を計算
[6] 母比率のz推定
標本比率から母比率を推定
\ P 〜 p ±z(α/2) \sqrt{ \frac{p(1-p)}{n}}
- z分布を活用
- サンプルサイズがn>=30
[7] 2つの母比率の差の検定
\ (P_1 - P_2) 〜 (p_1 - p_2) ±z(α/2) \sqrt{ \frac{p_1(1-p_1)}{n_1} +\frac{p_2(1-p_2)}{n_2} }
- サンプルサイズ大小問わずにz分布を活用
+α
必要なサンプルサイズ(母比率の区間推定)
信頼区間の幅は、
2 * 1.96 * \sqrt{\frac{p(1-p)}{n}}
[例]
推定値 $p = 0.1$, 信頼区間を5%以下にしたい
2 * 1.96 * \sqrt{\frac{0.1(1-0.1)}{n}} <= 0.05
*推定値が求められないときは、0.5を使う
*信頼区間の幅が最も大きくなるのが0.5のときなので
メモ
- 分散分析、独立性の検定、適合度の検定は、片側検定
- 母平均95%信頼区間 -- 母集団から標本を取ってきて、その平均から95%信頼区間を求めるという作業を100回やった時に95回はその区間の中に母平均が含まれる
- 信頼区間の幅は、$\sqrt{n}$ に反比例。よってサンプルサイズがk倍になると、信頼区間の幅は $\frac{1}{\sqrt{k}}$ 倍となる
- 分散分析>>母平均の差の検定:すべての母平均が等しい
- カイ二乗分布は自由度が大きくなると正規分布に近づく
- 重相関係数 >> 回帰式と予測値の相関係数。回帰式の当てはまりを評価。