統計検定2級の過去問を参考に、最低限に必要な定義や式をまとめたものです!
比較的問題になる傾向が多いところについて扱っていて、 全く網羅的ではないです
[追記]統計検定2級、おかげさまで合格しました。
※筆者が2級取得前にまとめたものであるため間違いがあればお手数ですがご指摘願います
※2017年11月までの過去問を参考にしているのですが、統計検定は毎年新しい形式の問題を出してきます
グラフとデータの扱い
分散や期待値、標準偏差と共分散はどれも必須の式
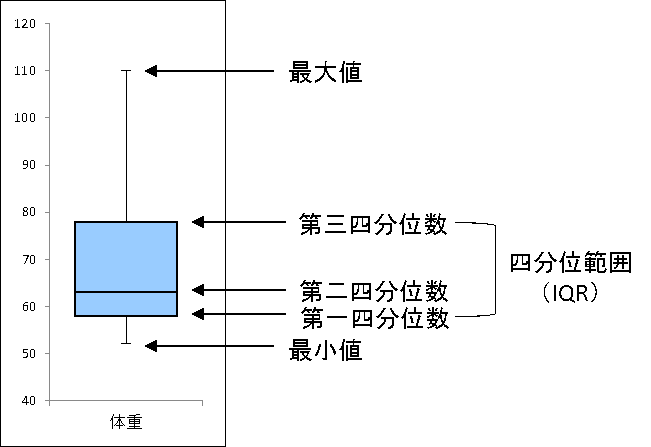
箱ひげ図
箱ひげは大雑把に言えば、データを小さい順に並べてだいたい同じデータ数になるように4つに分けた図のこと
あくまで どの変にデータが集まっている かがわかる
また、最低値と最大値、中央値もパッと見でわかるが、正確な平均値はわからない(よって分散などもわかるわけない)
用語については以下の図の通りで、「最大値」、「最小値」、「第一四分位数」、「第二四分位数」、「第三四分位数」を併せて5数要約というらしい
標準化
対象とするデータを$x$、全体の平均を$\overline x$、標準偏差を$s$として
標準化得点は
標準化得点=\frac{x-\overline x}{s}
分散
分散は データのばらつきの大きさ を示す。分散の式は、
V(x)=\frac{1}{n}\sum_{i=1}^n(x_i-\overline x)^2
例えば{5,3,7,8,12}なら平均が7で、平均との差を二乗して足し、最後にデータ数でわる
$(2^2+4^2+0^2+-1^2+-5^2)/5=46/5=9.2$
{6,6,9,7,7}なら平均は同じく7だが、
$(1^2+2^2+-2^2+0^2+0^2)/5=9/5=1.8$
なので後者のデータの方がばらつきが小さいことがわかる
また分散の式は以下のように 展開が可能
どちらかも足し算になってるところがミソ
V[aX+bY]=a^2V[X]+b^2V[Y]+2abCov[X,Y]\\
V[aX-bY]=a^2V[X]+b^2V[Y]-2abCov[X,Y]\\
(Cov(X,Y)は共分散)
標準偏差
基本的には分散の平方根である
ちなみに分散=$σ^2$と表すので、標準偏差は問題の中で求めやすいことが多い
標準偏差=\sqrt{分散}
二項分布における検定で用いられる場合は以下のような形にもなる
標準偏差=\sqrt{\frac{p(1-p)}{n}}
共分散
共分散の式は以下のよう、分散と違い平均との差を二乗するのではなくかけるところに注目
Cov(x,y)=\frac{1}{n}\sum_{i=1}^n(x_i-\overline x)(y_i-\overline y)
共分散、以下のように展開ができる
Cov[X+Y,X-Y]\\
= Cov[X,X]-Cov[X,Y]+Cov[Y,X]-Cov[Y,Y]\\
(ここでXとYが互いに独立な確率変数である場合は共分散は0)
= Cov[X,X]-0+0-Cov[Y,Y]
確率変数の共分散
また2つの確率変数の共分散を求める式は以下になる
Cov[X,Y]=E[(X-μ_x)(Y-μ_y)]
以下の式を使うと楽になる
Cov[X,Y]=E[XY] - μ_x μ_y
相関係数
すごくよく使う公式 の1つ、分子に共分散がいる
r=\frac{Cov(X,Y)}{\sqrt{V(X)}\sqrt{V(Y)}}
期待値と分散
これも覚えていないと解けない問題がよく出る
V(X)=E(X^2)-\{E(X)\}^2
期待値
期待値自体は高校で習った通りであって、例えばサイコロの出る目の期待値は3.5
期待値の式の展開、例えばx=0~1の範囲で$F(x)=X^2$の場合は
E(X)=\int_0^1x\cdot f(x)dx=\int_0^1x\cdot 2xdx\\
E(X^2)=\int_0^1x^2\cdot f(x)dx=\int_0^1x^2\cdot 2xdx\\
不偏分散
検定のタイミングで登場してくる不偏分散
$u^2$ = 不偏分散
u^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i-\overline x)^2
検定
検定が2級のメインになるし、統計学としても実用に近いところ
全体の5~7割は検定の問題 になる
帰無仮説の棄却
検定の基本となる用語たち
帰無仮説 = 検定するための仮説、現状で妥当な方を置くことが多い
対立仮説 = 帰無仮説に対する仮説、 本来証明したいこと を置くことが多い
棄却 = 仮説を捨てること、基本的には帰無仮説を棄却しようとする試みが検定である
有意水準 = 帰無仮説を棄却する基準(XX%とかで示される)
正規分布
統計学的に一番よくある分布で、左右対称のベルカーブをしている
平均を$μ$、分散を$σ^2$とすると
$N(μ,σ^2)$ と表せる
問題の例としては、統計量を導き出してから、その統計量を用いて付録として付いてくる 標準正規分布の上側確率の表 を用いて確率を導く問題が多い
例えば、「$N(50,100)$の分布に従うデータにおいて個体の値が60より大きくなる確率は?」という問題
P(X)=\frac{X-μ}{\sqrt{σ^2}}\\
P(X=60)=\frac{60-50}{\sqrt{100}}\\
= 1.0
これで1.00が統計量となるため、表を読むと0.1587が上側確率であるということがわかる
ちなみに、正規分布は左右対称であるため、上側確率だけで「以下」の方も求められる
また別の例として「サンプルサイズが100の標本平均が52以上になる確率は?」みたいに 標本平均 をテーマにした問題においては
サンプルサイズを加味した分散を用いることで同じ式で解ける
P(X)=\frac{X-μ}{\sqrt{\frac{σ^2}{n}}}\\
P(X=60)=\frac{52-50}{\sqrt{100/100}}\\
= 2.0
これで2.00が統計量となるため、表を読むと0.0228が上側確率であるということがわかる
母平均の信頼区間(95%)
母平均の推定と母比率の推定は実用的なのでよく問題にも使われる
1.96は上側確率0.025の値
\overline X -1.96 \times\frac{σ}{\sqrt{n}}
≦
μ
≦
\overline X +1.96 \times\frac{σ}{\sqrt{n}}
母分散の信頼区間(95%)
\frac{(n-1)S^2}{\chi^2_{0.025}(n-1)}
≦
σ^2
≦
\frac{(n-1)S^2}{\chi^2_{0.975}(n-1)}
母比率σの信頼区間(95%)
母平均の推定と母比率の推定は実用的なのでよく問題にも使われる
1.96は上側確率0.025の値
\overline p -1.96\times\sqrt{\frac{\overline p (1-\overline p)}{n}}
≦
p
≦
\overline p +1.96\times\sqrt{\frac{\overline p (1-\overline p)}{n}}
標本誤差と統計量
$\hat μ$ = 推定平均
$μ$ = 母平均
P \geq \frac{\hat μ-μ}{標本誤差}\\
標本標準偏差と標準誤差
標本標準偏差はその名の通り標本の標準偏差
ただし、n-1でわるので注意
s=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n} (x_i-\overline x)^2}
標準誤差は標本標準偏差をサンプルサイズの平方根で割る
標準誤差 = \frac{標準偏差}{\sqrt{サンプルサイズn}}
これを踏まえて母比率の区間推定の式を見ると何か見えてくる
二項分布の性質
$Y_n$が二項分布$B(n,p)$に従う場合、
E[Y_n]=np\\
V[Y_n]=np(1-p)\\
が成り立ち、パラメータ$p$の推定量$\overline Y_n=\frac{Y_n}{n}$の分散は
V[Y_n]=\frac{p(1-p)}{n}\\
となる
この式を見ると、分散を最大にするのは確率が50%(p=0.5)の時だということがわかる
ポアソン分布
二項分布において期待値をnp=λとして固定して試行回数をn→∞、p→0として、「ごく稀にしか起きない現象」とする場合に利用できる分布である
「ある期間に平均λ回起こる現象が、ある期間にk回起きる確率の分布」とも言い換えることができる
$λ$ = 期待値、今回であれば「全体の平均」として使うことができる
$X$ = 試行回数,(X=kとして利用)
P(X=k)=\frac{e^{-λ}λ^k}{k!}
例として、平均2.1回起こる事象(ポアソン分布に従う)が3回起こる確率は
P(X=2)=\frac{e^{-2.1}2.1^3}{3\cdot2\cdot1}=0.189
ポアソン分布でポイントになるのは、パラメータが$λ$の時、平均も分散も$λ$になるというこも
t検定
$s^2$ = 不偏分散
$μ_0$ = 平均(試行前)
$\overline X$ = 検定対象の平均(試行後)
$t$ = 統計量
$n$=サンプルサイズ
t=\frac{\overline X- μ_0}{\frac{s}{\sqrt{n}}}
t値
回帰分析において
t = \frac{傾きの推定値(偏回帰係数)}{標準誤差}
誤差分散の推定値
\hat σ^2=\frac{1}{n-2}\sum_{i=1}^n e_i^2=\frac{1}{n-2}\sum_{i=1}^n (y_i-\hat y_i)^2
変動係数
$d$ = 変動係数
$μ$ = 母平均
$σ$ = 標準偏差
$n$ = サンプルサイズ
d=\frac{\sqrt{\frac{σ^2}{n}}}{μ}
問題によっては全体の変動係数ではなく1つのサンプルの変動係数を求めさせる時がある
その場合は $n=1$ で計算することになる
クロス集計表の相関関係
| 人数 | $y_i=0$ | $y_i=1$ | 合計 |
|---|---|---|---|
| $x_i=0$ | a | b | a+b |
| $x_i=1$ | c | d | c+d |
| 合計 | a+c | b+d | n |
上記の場合に以下が成り立つ
r=\frac{ad-bc}{\sqrt{a+b}\sqrt{c+d}\sqrt{a+c}\sqrt{b+d}}
χ二乗の統計量
まずは期待度を求める、
例えば以下の例があった場合に
| はい | いいえ | |
|---|---|---|
| 男 | 80 | 40 |
| 女 | 40 | 60 |
| 合計 | 120 | 100 |
「全体の比率と同じ比率で分布する、性別での相関が何もない場合の数値が期待度になる
今の例だと全体で 「はい」:「いいえ」=120:100 の比率なので
男の「はい」を選択する期待度は65.5、「いいえ」を選択する期待度は54.5
女の「はい」を選択する期待度は54.5、「いいえ」を選択する期待度は45.5
| はい | いいえ | |
|---|---|---|
| 男 | 65.6 | 54.5 |
| 女 | 54.5 | 45.5 |
| 合計 | 120 | 100 |
以上の場合に、以下の式で求められる
\chi^2=\frac{(80-65.5)^2}{65.5}+\frac{(40-54.5)^2}{54.5}+\frac{(40-54.5)^2}{54.5}+\frac{(60-45.5)^2}{45.5}
F分布
確率変数$W_1$,$W_2$が$\chi$二乗分布に従い、自由度がそれぞれ$m_1$,$m_2$である場合に下記は自由度$(m_1,m_2)$のF分布に従う
\frac{\frac{W_1}{m_1}}{\frac{W_2}{m_2}}
詳細に書くと自由度$(m_1,m_2)$のF分布は次の式で表される
f(x)=\frac
{\Gamma(\frac{m_1+m_2}{2})(\frac{m_1}{m_2})^{\frac{m_1}{2}}x^{\frac{m_1}{2-1}}}
{\Gamma(\frac{m_1}{2})\Gamma(\frac{m_2}{2})(1+\frac{m_1}{m_2}x)^{\frac{m_1+m_2}{2}}}
\space\space\space\space\space(0<x<\infty)
またF値は以下のようにして求められる
F=\frac{\frac{水準間平方和}{水準間自由度}}{\frac{残差平方和}{残差自由度}}
検出力
帰無仮説が間違っていた時にちゃんと帰無仮説を棄却できる確率のこと
「第二種の過誤」の確率がβなら検出力は1-β
不偏定数量と一致推定量
不偏推定量 とは大雑把に、 平均的には、真の値を正しく予測できるような推定量 である
例えば標本の平均の期待値が母平均と等しい場合はその標本平均は不偏推定量である
一致推定量 とは大雑把に、 サンプル数をどんどん増やしていくとほぼ確実に、真の値を正しく予測できるような推定量 です。
標本平均は不偏推定量であり、一致推定量でもある。そのため、標本平均の値を母平均の推定量として使うことができる
第一種の過誤・第二種の過誤
1,2問は出てくるので言葉の意味・定義を覚えておく必要がある
第一種の過誤(α): 帰無仮説が真であるのにもかかわらず、帰無仮説を偽として 棄却してしまう 誤りのこと
第二種の過誤(β): 帰無仮説が偽であるのにもかかわらず、帰無仮説を 棄却しない 誤りのこと
回帰分析
毎年最後の3問くらいは回帰分析の出力結果からの出題が多い
回帰モデル
いくつかの例を並べる
基本的に左上の数値を右下の数値で割れば欲しい数値が求められる
平均平方であれば $\frac{平方和}{自由度}$、F値であれ$\frac{要因の平均平方}{残差の平均平方}$
| 因子 | 平方和 | 自由度 | 平均平方 | F値 |
|---|---|---|---|---|
| 要因 | 1108.25 | 6 | 184.71 (平方和÷自由度) | 0.926 (要因の平均平方÷残差の平均平方) |
| 残差 | 7976.86 | 40 | 199.42 (平方和÷自由度) | - |
| 全体 | 9085.11 | 46 | - | - |
| 要因 | 平方和 | 自由度 | 平均平方 | F値 | Pr(>F) |
|---|---|---|---|---|---|
| 地域 | 0.2204 | 3 | 0.07347 | 3.488 | 0.0405 |
| 残差 | 0.3370 | 16 | 0.02106 | - | - |
| 全体 | 0.5574 | 19 | - | - | - |
| 推定値 | 標準誤差 | t値 | P-値 | |
|---|---|---|---|---|
| 切片 | 452.011 | 2.147 | 210.56 | 0.00 |
| 時間変数 | 0.937 | 0.0429 | 21.86 | 0.00 |
確率
加法定理はそんなに問題として取り上げらない
条件付き確率はよく出る
確率の加法定理
$P(A)$ = Aが起こる確率
$P(B)$ = Bが起こる確率
$P(A\cup B)$ = AもしくはBが起こる確率
$P(A\cap B)$ = AとBが同時に起こる確率
$P(A\cup B)= P(A)+P(B)-P(A\cap B)$
条件付き確率
$P(B|A)$ = Aが起こるという条件の元でBが起こる確率は
P(B|A)=\frac{P(A\cap B)}{P(A)}
参考
(参考)二項分布の統計量を求める式と正規分布の統計量を求める式の比較
$p(1-p)$ = 二項分布において2パターンそれぞれの確率をかけてる
$n$ = サンプルサイズ
$X$ = 確率変数
似てる
\frac{X-np}{\sqrt{np(1-p)}}≒\frac{\hat p-p}{\sqrt{\frac{p(1-p)}{n}}}