はじめに
この記事はHappy Elements Advent Calendar 2020の22日目の記事になります。
データアナリストとしての立場で書かせていただきます。
本記事の内容
Happy Elements株式会社では「Make The World Happy!」というスローガンを掲げ、「ゲーム」を通じた喜びや感動をお届けすることで、沢山の人々にほんの少しでも幸せを感じてもらうことを目指しています。
そういった活動の中で、データ分析チームは、ゲームの「現状を知り、お客様に盛り上がっていただくためのボトルネックを解消する」ための分析を日々しています。
本記事では、そんな分析の中から、一番最初に行う「現状を知る」ための手法を一つご紹介させていただこうと思います。
内容としては「ベイズ推論によるイベント参加率の比較」です。
作業はGoogle Colab上で行い、主なツールとしてPyMC3を使います。
PyMC3は2020年12月7日に、JAXを使ったNUTSサンプリングが可能となったver3.10.0がリリースされています。
今回はそのver3.10.0を使い、噂のJAXを使った場合の処理時間の改善具合なども見ていきたいと思います。
処理時間比較は本記事の最後に記載していますので、興味がある方は下の方を御覧ください。
問題設定
A = pd.DataFrame(np.random.choice([0,1],10000, p=[0.3,0.7]), columns=["flag"])
B = pd.DataFrame(np.random.choice([0,1],16000, p=[0.25,0.75]), columns=["flag"])
C = pd.DataFrame(np.random.choice([0,1],13000, p=[0.305,0.695]), columns=["flag"])
| イベント | アクティブ数 | 参加数 | 参加率 |
|---|---|---|---|
| A | 10,000 | 7,028 | 70.28% |
| B | 16,000 | 12,016 | 75.10% |
| C | 13,000 | 8,962 | 69.45% |
このようなデータを用意しました。
このデータを元に、イベントA・B・Cの参加率に差があるのか、またその差がどの程度なのかをベイズ推定を用いて見ていきます。
PyMC3.10.0の準備
Google Colabで下記を実行することで必要なモノが揃います。
必要に応じてimportしてください。
!pip uninstall theano -y
!pip install theano-pymc
!pip install pymc3==3.10.0
!pip install numpyro
!pip install tfp-nightly
モデルの設計
特に凝ったことはせず、シンプルに設計して行きます。
事前分布を一様分布とし、ベルヌーイ分布で表します。
\begin{align}
p\quad&\sim \quad Unifrom(\,\,0\,,\,\,1\,) \\
obs\quad &\sim\quad Bernoulli(\,\,p\,\,)
\end{align}
これをA~C分Colab上での記述します。
with pm.Model() as model:
p_A = pm.Uniform('p_A', 0, 1.0)
p_B = pm.Uniform('p_B', 0, 1.0)
p_C = pm.Uniform('p_C', 0, 1.0)
obs_A = pm.Bernoulli("obs_A", p_A, observed=A.flag)
obs_B = pm.Bernoulli("obs_B", p_B, observed=B.flag)
obs_C = pm.Bernoulli("obs_C", p_C, observed=C.flag)
事前分布を一様分布の0~1で表していますが、これはベルヌーイ分布の共役事前分布であるベータ分布のα=1、β=1と同様になります。
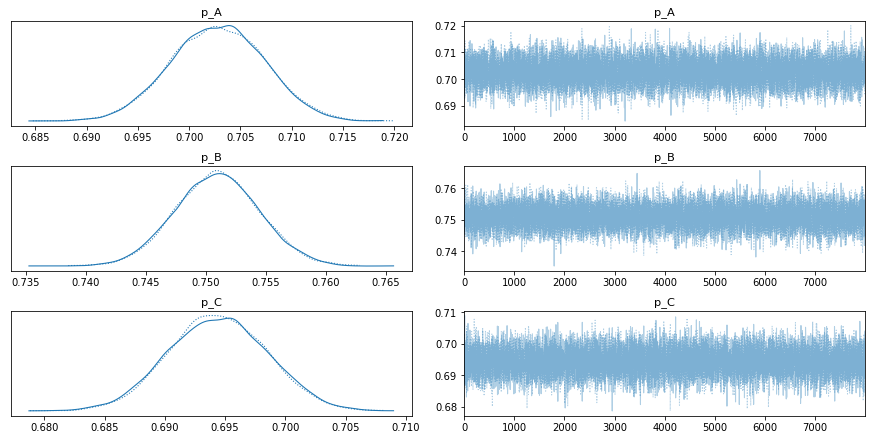
サンプリング
%%time
with model:
trace_nuts = pm.sample(8000, tune=2000, chains=2, target_accept=0.8)
> Wall time: 1min 27s
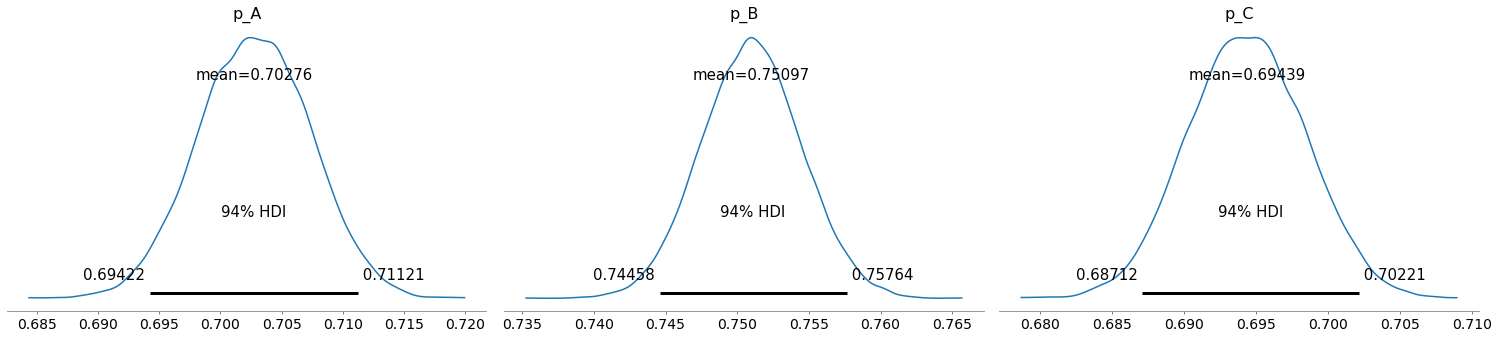
期待値mean=確率もある程度いい感じに合っていそうですね。
確率分布の比較
plt.figure(figsize=[20,10])
plt.hist(trace_nuts.p_A,bins=200, alpha=0.3, label="A",density=True)
min_ylim, max_ylim = plt.ylim()
plt.axvline(trace_nuts.p_A.mean(), color='k', linestyle='dashed', linewidth=1)
plt.text(trace_nuts.p_A.mean()+0.001, max_ylim*0.9, 'Mean: {:.3f}'.format(trace_nuts.p_A.mean()),fontsize=20)
plt.hist(trace_nuts.p_B,bins=200, alpha=0.3, label="B",density=True)
plt.axvline(trace_nuts.p_B.mean(), color='k', linestyle='dashed', linewidth=1)
plt.text(trace_nuts.p_B.mean()+0.001, max_ylim*0.8, 'Mean: {:.3f}'.format(trace_nuts.p_B.mean()),fontsize=20)
plt.hist(trace_nuts.p_C,bins=200, alpha=0.3, label="C",density=True)
plt.axvline(trace_nuts.p_C.mean(), color='k', linestyle='dashed', linewidth=1)
plt.text(trace_nuts.p_C.mean()+0.001, max_ylim*0.8, 'Mean: {:.3f}'.format(trace_nuts.p_C.mean()),fontsize=20)
plt.legend(loc='upper right', borderaxespad=1, fontsize=18)
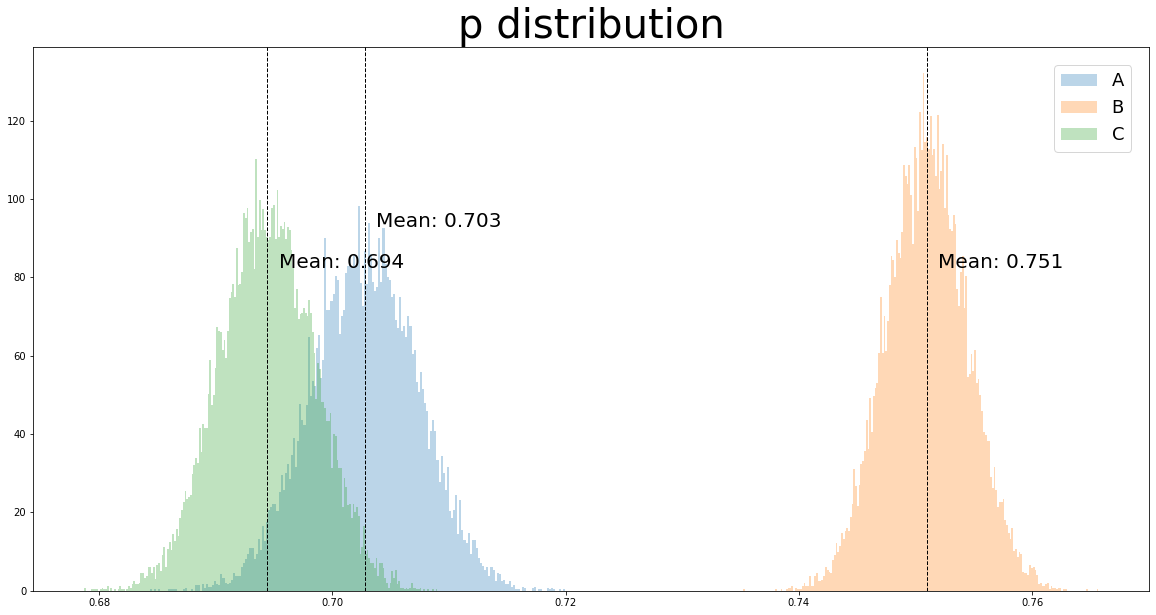
plt.title("p distribution",fontsize=40)
Bは他の2つと比べて明確に参加率が高そうです。
AとCに関しては一部被っており、どの程度の差があるのか計算が必要です。
ベイズ推定により確率分布で求めたメリットが生きてきます。
plt.figure(figsize=[20,10])
plt.hist(trace_nuts.p_A - trace_nuts.p_C,bins=200, alpha=0.3, label="delta A-C",density=True,color="r")
min_ylim, max_ylim = plt.ylim()
plt.axvline(0, color='k', linestyle='dashed', linewidth=1)
plt.text(0+0.01, max_ylim*0.5, 'A: {:.3f}%'.format((trace_nuts['p_A'] - trace_nuts['p_C'] > 0).mean()*100),fontsize=30)
plt.text(0-0.01, max_ylim*0.5, 'C: {:.3f}%'.format(100-(trace_nuts['p_A'] - trace_nuts['p_C'] > 0).mean()*100),fontsize=30)
plt.legend(loc='upper right', borderaxespad=1, fontsize=18)
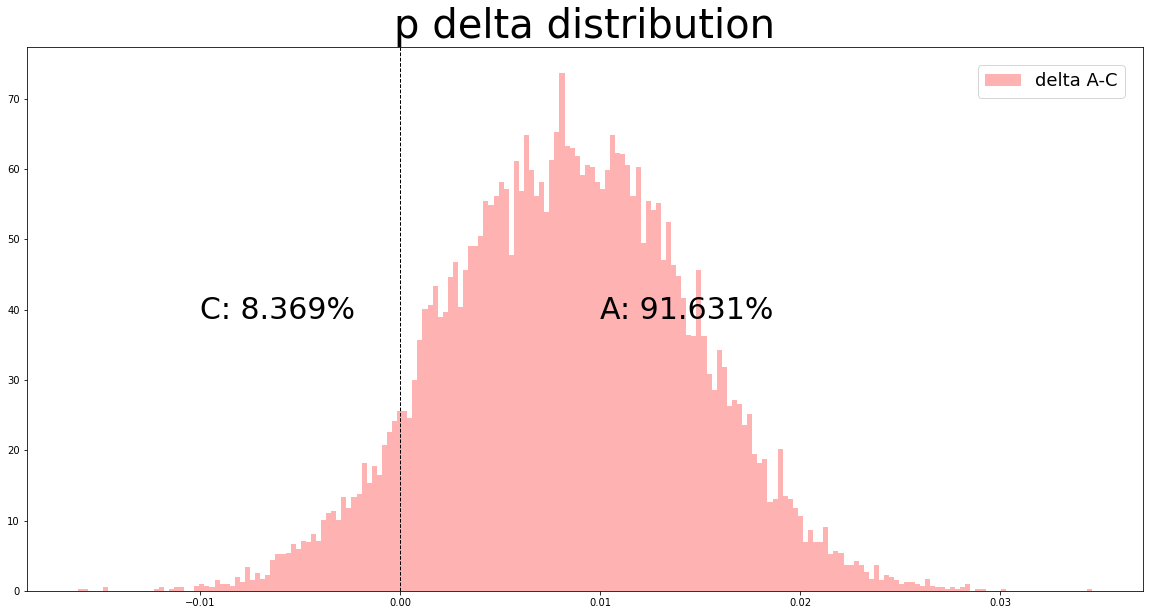
plt.title("p delta distribution",fontsize=40)
Cに対するAの勝率は91.63%であることがわかりました。
90%を超えていればまあ勝ち、80%台だと大負けすることは無いが明確に勝ちとは言えない程度、として扱っています。
このように勝率で差を語れることが確率分布での比較のメリットだと感じています。
簡単な注意ですが、「差がある」「勝率で語れる」というのは、現実世界の話ではなくあくまで数学的な統計モデル間の話であることを注意してください。
最後に
ここまでイベントA・B・Cの参加率に差があるのかをベイズ推定で試す流れを見てきました。
やっていること、していること自体は非常に単純なものですが、ここはまだまだデータ分析の入り口です。
各イベントの相対的な差がわかったところで、なぜ差が出来るのか、何が要因で参加率が上がるのかといった課題の解明に取り組んで行きます。
影響がありそうな説明変数を切り出していき、階層ベイズモデルなどで表してみたりしています。
簡単に正解がわかるようなモノではありませんが、やりがいのある楽しい仕事です。
これからも、弊社のゲームを通しお客様に今まで以上に盛り上がっていただくために、仲間のゲームクリエーター達と励んでいきたいと思います。
PyMC+JAXの時間比較
ここがメインまである、PyMC純正NUTSとnumpyroのNUTS、TFPのNUTSの処理時間比較のコーナーです。
■PyMC
%%time
with model:
trace_nuts = pm.sample(8000,tune=2000,chains=2,target_accept=0.8)
> Wall time: 1min 27s
■numpyro_nuts
%%time
with model:
trace_jax_numpyro = pm.sampling_jax.sample_numpyro_nuts(8000, tune=2000, chains=2,target_accept=0.8)
> Wall time: 19.9 s
■tfp_nuts
%%time
with model:
trace_jax_tfp = pm.sampling_jax.sample_tfp_nuts(8000, tune=2000, chains=2,target_accept=0.8)
> Wall time: 35 s
87 / 19.9
> 4.371859296482413
PyMCとnumpyro_nutsを比べると約4.37倍の速度になっています。
素晴らしいですね。
JAXを使ったsliceサンプリングなども用意が進んでいるようですので、今後の開発が楽しみです。
メンバー募集
Happy Elements株式会社 カカリアスタジオでは、いっしょに【熱狂的に愛されるコンテンツ】をつくっていただけるメンバーを大募集中です!
もし弊社にご興味持っていただけましたら、是非一度下記採用サイトをご覧ください。