要約
紙の端を利用して自炊画像が何度傾いてるか検知できたというお話。
緑色の線が紙の端として検知した直線です。この直線の傾きが画像の傾きそのものです。
最下部にソース(Java)を掲載しています。
【追記】
この記事の手法で検知できるのはスキャン時の「紙の傾き」です。「印刷の傾き」は検知できません。
印刷の傾きを検出するにはもう少し高度な画像処理手法(特徴抽出とか)が必要になると思います。
背景
最近、自炊(本のほう)をはじめました。が、どうも傾きが気になることがあります。スキャナの本体、もしくは読み取りソフトに傾き補正機能がついているのですが、精度がいまいちな気がします。そこで、自分で傾き検知用のプログラムを書いてみたのでメモします。
手順
(1)紙の端を走査
(2)最小二乗法で直線近似
(3)誤差の集計
(4)誤差平均が許容範囲内なら(7)へ
(5)誤差の大きい点を除去
(6)(2)に戻る
(7)近似直線から傾きを求める
手順の説明
このアルゴリズムの基本的な発想は紙の端の検知です。本はもともと綺麗な長方形であるはずなので、端の直線を検知できれば画像の傾きが求められるはずです。
ここでは以下の様な画像を例に手順を追って説明します。(わかりやすいように極端に傾けています)
走査
紙の左端を検出します。
左から右、上から下という方向で走査し、白色になった座標を左端の座標ということにします。

(赤色の点が走査した点)
「ということにする」というのは、「本当に紙の左端だかわからないけどとりあえず左端だということにしておく」ということです。画像を見ても分かる通り、左端以外の点も含まれてしまっていますが、この時点ではそれでよしとします。
最小二乗法で直線近似
上記の方法で集まった座標に対して、とりあえず最小二乗法で直線を近似します。特に難しいこともなくy = ax + bが求まります。
正しいかどうかわからない座標に対して直線を近似しても仕方ないと思われるかもしれません。確かに、上の画像でも全く見当違いの直線を近似してしまっています。
二乗誤差の集計
しかし、もちろん無意味ではありません。なぜなら、正しい直線を走査できていれば近似線と走査座標は重なるからです。逆にいうと、近似線と走査座標が重なっていないのなら、誤った座標を元に近似しているからだと判断できるのです。
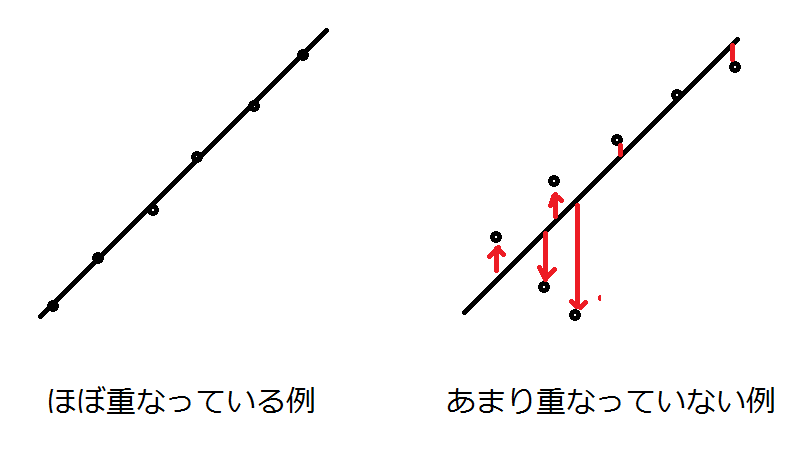
この「近似直線と走査座標の重なり具合」は、以下の式で求めます
\sqrt{\frac{\sum_{i=1}^n \left(走査座標_iのy座標-近似直線のy座標\right)^2} {n}}
この値が大きければ大きく離れているし、0に近ければほぼ重なっているため正しい直線を検出できたと判断できます。
ちなみに、上の式は、要するに近似直線と走査座標が平均してどれくらい離れているかということを求めています。「Σ」とか使ってますが基本は「誤差の合計/要素数」という平均を求める式です。誤差を2乗しているのは、誤差には正負があるので普通に総和すると打ち消し合ってしまうからです。平方根を取っているのは、「2乗したんだから元に戻さないとね」程度の理由だと思います1。
誤差の大きい点を除去
誤差平均が大きかった場合、誤差が大きかった点を除去します。近似直線から離れた座標は外れ値である可能性が高いからです。
除去した座標で再近似
外れ値を除去した座標を利用して再度直線を近似します。最初の図より少しだけ実際の先に近づきましたね。
繰り返し
これを繰り返すと、最終的に近似線と左端はほぼ重なって行くのがわかると思います。
誤差平均が許容誤差以下になったところで、紙の端を検知できたと判断して計算を打ち切ります。
近似直線から傾きを求める
直線が求まれば、その直線の傾きがそのまま紙の傾きです。この例の場合、直線の傾きは-45度でした。
適用例
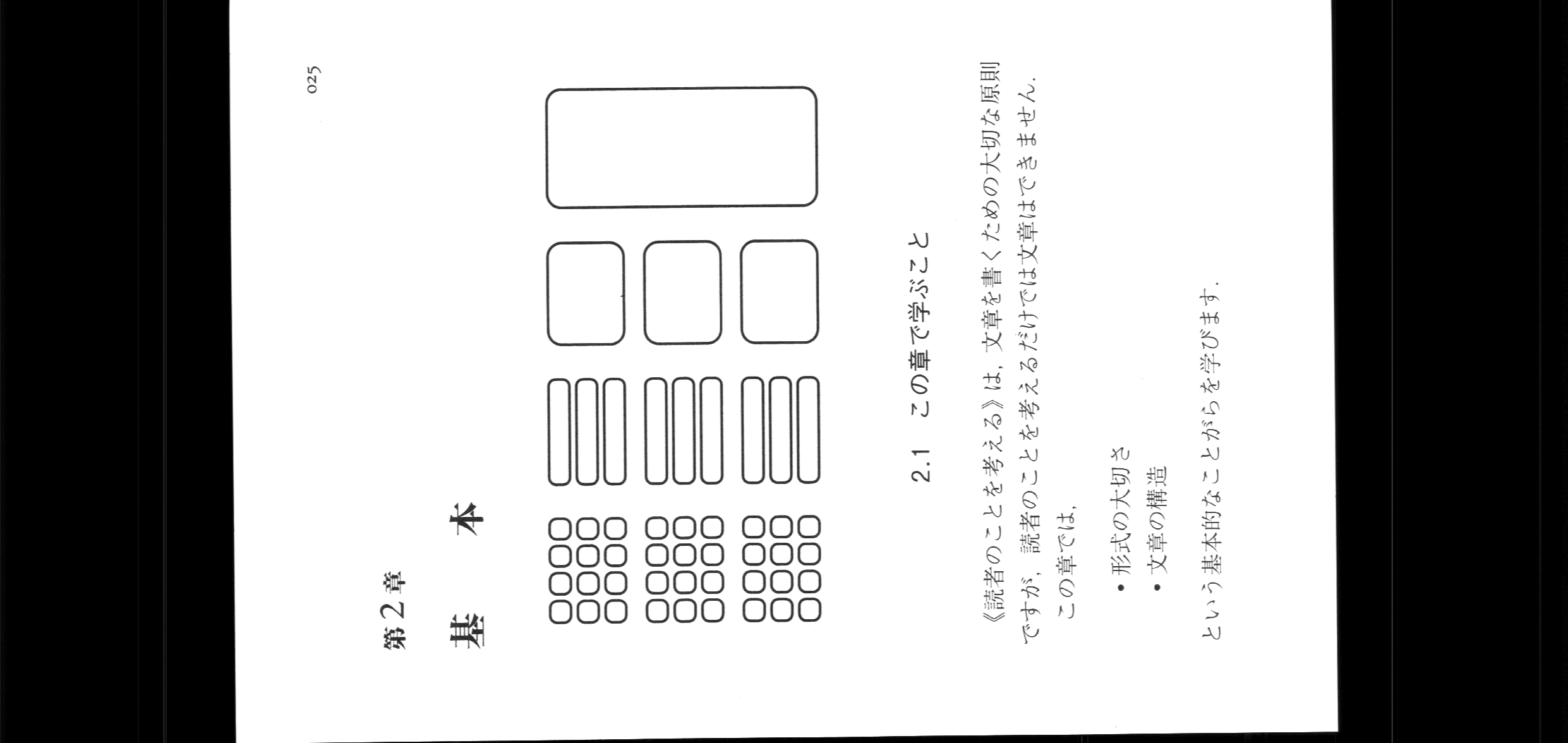
せっかくなので、実際の自炊画像をつかって試してみます。ここでは結城浩さんの「数学文章作法 基礎編」を例にしてみます。
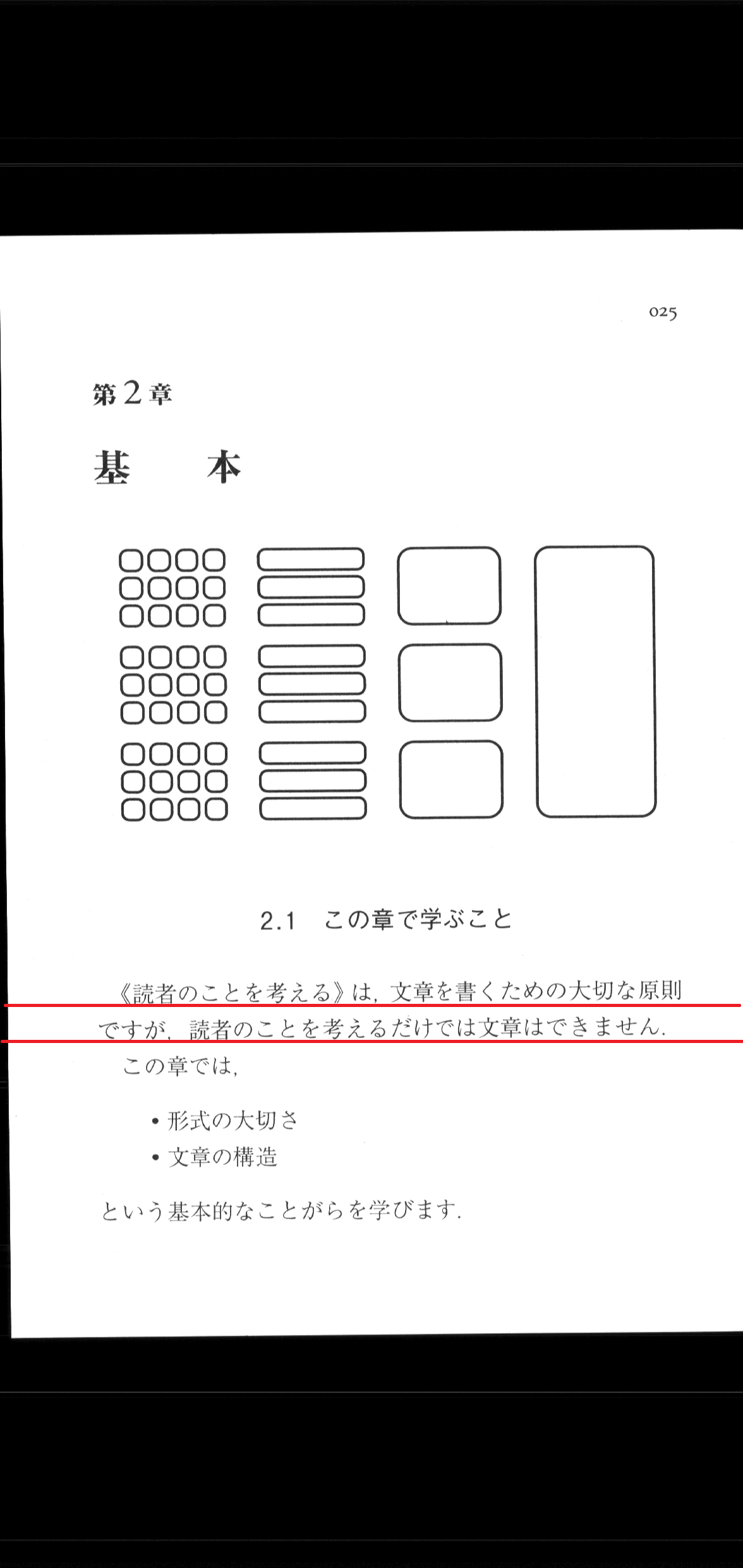
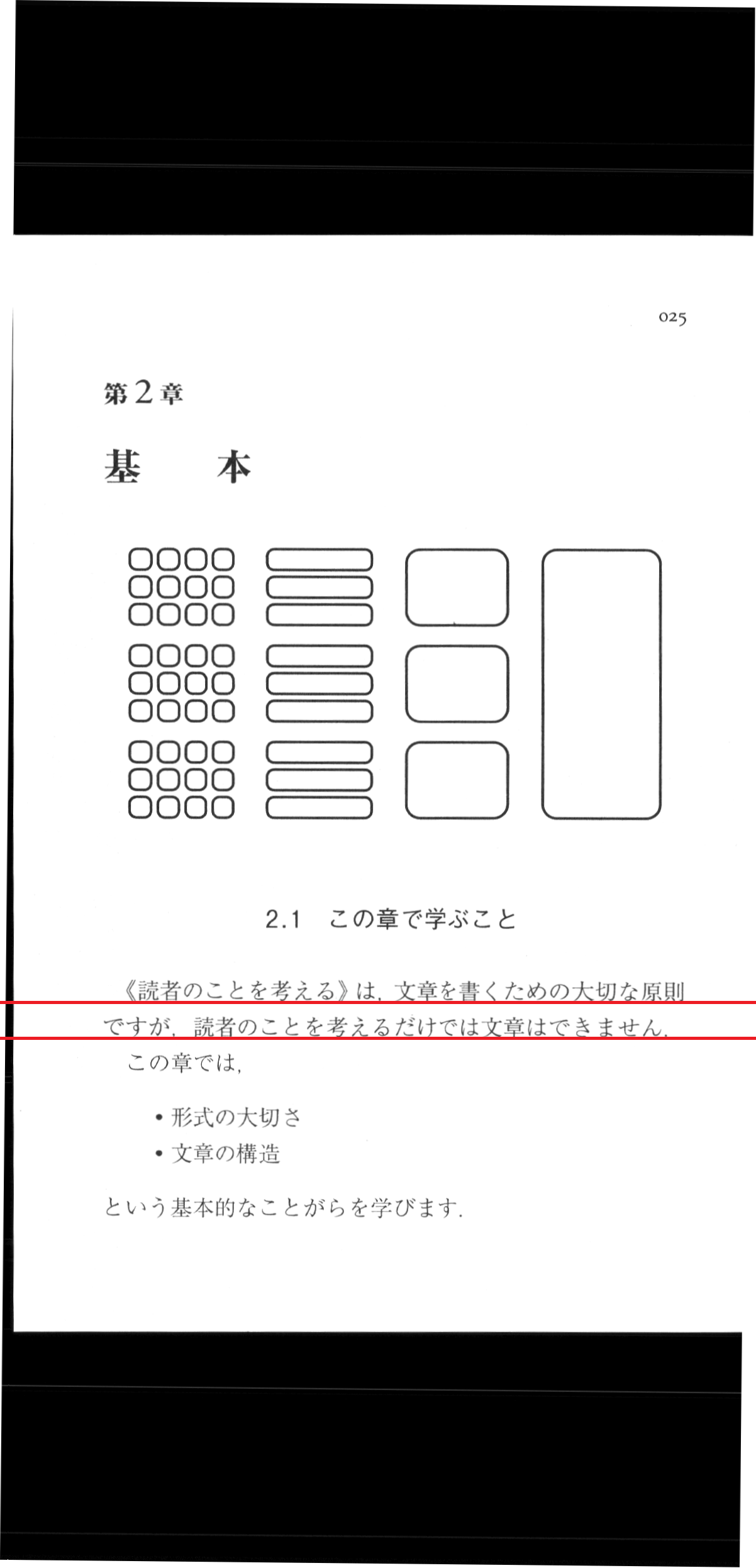
この画像を先ほどの手順通りに実行したところ0.58度の傾きという結果がでました。ではこの画像を90度、90.58度回転させた結果を比べてみます。
左が90度、右が90.58度回転させたものです。
本当に微妙な差ですが、90度の方はほんの少しだけ右上がりになっているのに対し、90.58度の方は傾きがほとんどなくなっているのがわかりますでしょうか??
(赤い補助線は補正後に書き足しています。)
終わりに
反復法で誤差を収束させるアルゴリズムなので速度面では不利ではありますが、ほとんどパラメータのチューニングなしにそれなりの精度が出るので結構使えるのではないでしょうか。
それにしても、理論ではわかっても実装して動かしてみると感動するもんですね。
ソース
※このソースは傾きを求めるところまでしか行いません。画像の回転は別途行う必要があります。
※また、上の画像のような赤の点や緑の線は出力しません。
import java.awt.image.BufferedImage;
import java.io.File;
import javax.imageio.ImageIO;
/**
* スキャン画像の傾きを求める
*/
public class TiltCorrector {
/**
* サンプリング個数。50程度で充分な精度が出る
*/
private static final int SAMPLING_NUM = 50;
/**
* 許容二乗誤差平均平方根
*/
private static final double ALLOWABLE_ERROR = 0.01;
/**
* 画像ファイルのパス
*/
private static final String IMAGE_PATH = "c:\\temp\\input.png";
/**
* メイン関数
*/
public static void main(String[] args) {
try {
// 画像読み込み
BufferedImage img = ImageIO.read(new File(IMAGE_PATH));
// 紙の左端を走査する
Point[] point = new Point[SAMPLING_NUM];
scanPoints(img, point);
// 反復法のループ
Line line = null;
int iterate = 0;
while (true) {
iterate++;
// 最小二乗法で直線(x = ay + b)を近似
line = lineSt(point);
// 近似直線と走査値を比較
ErrorInfo errorInfo = getErrorInfo(point, line);
// 許容誤差の範囲に収まったらループ終了
if (errorInfo.average <= ALLOWABLE_ERROR) {
break;
}
// 最も誤差が大きい座標を無視する
point[errorInfo.maxErrorIndex].isIgnore = true;
// 残り3点になっても収束しなければエラー
if ((SAMPLING_NUM - iterate) <= 3) {
throw new Exception("誤差が収束しない");
}
}
// 角度を表示
System.out.println(line.getDegree());
} catch (Exception e) {
e.printStackTrace();
}
}
/**
* 紙の左端を求める。
*/
private static void scanPoints(BufferedImage img, Point[] point) {
// yの間隔を求める
double dy = (img.getHeight() / (double) point.length);
// y軸方向スキャン
for (int i = 0; i < point.length; i++) {
int y = (int) Math.round(i * dy);
// x軸方向スキャン
for (int x = 0; x < img.getWidth(); x++) {
int rgb = img.getRGB(x, y);
if (isWhite(rgb, 200)) {
// 二値化した時に白色ならその座標を紙の端と判断する
point[i] = new Point(x, y, false);
break;
}
}
// 端を検知できなければ無視ポイントとしておく
if (point[i] == null) {
point[i] = new Point(-1, -1, true);
}
}
}
/**
* 最小二乗法で直線を求める。
*/
private static Line lineSt(Point[] point) {
int n = 0;
double sum_x = 0;
double sum_y = 0;
double sum_xy = 0;
double sum_x2 = 0;
for (int i = 0; i < point.length; i++) {
if (point[i].isIgnore) {
continue;
}
n++;
sum_xy += point[i].x * point[i].y;
sum_x += point[i].x;
sum_y += point[i].y;
sum_x2 += Math.pow(point[i].x, 2);
}
double a = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - Math.pow(sum_x, 2));
double b = (sum_x2 * sum_y - sum_xy * sum_x) / (n * sum_x2 - Math.pow(sum_x, 2));
return new Line(a, b);
}
/**
* 誤差を集計する
*/
private static ErrorInfo getErrorInfo(Point[] point, Line line) {
ErrorInfo errorInfo = new ErrorInfo();
int n = 0;
double maxError = Double.NEGATIVE_INFINITY;
double errorSum = 0.0;
for (int i = 0; i < point.length; i++) {
if (point[i].isIgnore) {
continue;
}
n++;
// y座標だと垂直に近い場合に誤差が大きいので代わりにx座標の差を求める
int xe = (int) Math.round((point[i].y - line.b) / line.a);
int xs = point[i].x;
double error = Math.pow(xe - xs, 2);
errorSum += error;
if (maxError < error) {
maxError = error;
errorInfo.maxErrorIndex = i;
}
}
errorInfo.average = Math.sqrt(errorSum / n);
return errorInfo;
}
/**
* 画素が白であるなら trueを返す
*/
public static boolean isWhite(int rgb, int threshold) {
int r = (rgb & 0x00FF0000) >> 16;
int g = (rgb & 0x0000FF00) >> 8;
int b = rgb & 0x000000FF;
int average = (r + g + b) / 3;
return threshold <= average;
}
/**
* 誤差を記録するためのValueObject
*/
private static class ErrorInfo {
double average;
int maxErrorIndex = -1;
}
/**
* 座標を記録するためのValueObject
*/
private static class Point {
int x, y;
boolean isIgnore;
Point(int x, int y, boolean isIgnore) {
this.x = x;
this.y = y;
this.isIgnore = isIgnore;
}
}
/**
* 直線を表すValueObject
*/
private static class Line {
double a, b;
Line(double a, double b) {
this.a = a;
this.b = b;
}
private double getDegree() {
return Math.atan(1 / a) * 180 / Math.PI;
}
}
}
-
機械学習とか、統計などの分野ではこのような2乗誤差の平均平方根をよく見ます。多分ですが、この形だと微分できるから数式で理論をこねくりまわせて便利なんだと思います。 ↩