RevComm の裏側で動くアルゴリズム [二分探索編]

はじめに

この記事は 2020 年の RevComm アドベントカレンダー 14 日目の記事です。 13 日目は @shintaromatsudo さんの 「Python × Elasticsearchで検索と集計をしてみよう」 でした。

こんにちは、 RevComm で web アプリケーション、解析システムの開発をしている @tatakahashi です。
学生時代、競技プログラミングにハマっていたのですが、そこで身に付けた技が業務に役立ったのでその事例を紹介します。
私は競プロでは c++ を使いますが、今回は業務でよく書く python を使います。( c++ も業務で使います)

今回は二分探索編です。
界隈では「にぶたん」なんて呼んだりしますが、ここでは「二分探索」と表記することにします。

探索

探索とは「条件に合う何か」を探すことです。
探索アルゴリズムをうまく使うことで探しているものを見つけることができます。(見つからないかもしれません)

問題設定として、長さ $ N $ のソート済み配列 $ A $ が与えられた時、配列の中にある値 $ X $ の添字を知りたいというシチュエーションを考えます。

線形探索

まずは線形探索からです。一番素朴なのは前から順番に見ていく方法でしょう。
こんな感じです。

for i in range(N):
    if A[i] == X:
        print(f'index: {i}')
        break

しかしこれでは、配列の後ろの方に $ X $ がある場合に時間がかかってしまいます。だったら後ろから見ればいいじゃないかと思いますが、 $ X $ がどこにあるかは分からないので、見る順番をあれこれ試してもいろんなパターンには対応できません。
乱数を利用するのも同様です。配列の中に当たりは 1個という状況でサイコロ振るのは得策ではなさそうです。

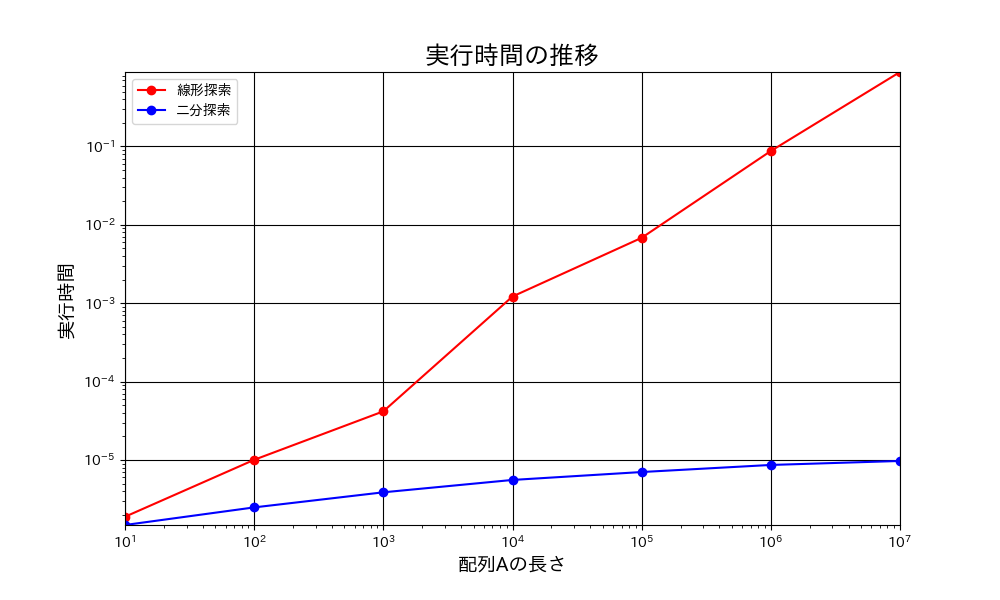
線形探索と二分探索の実行時間の比較

非常にシンプルに書けるというメリットの一方で、配列サイズが大きいと時間がかかるデメリットがあります。
高速化したくなりますね！

二分探索

二分探索は、見つけたいものが配列内のどこにあっても高速に見つけられるアルゴリズムです。

「二分探索」という言葉は聞き慣れないかもしれませんが、実生活では使ったことがあるはずです。
辞書を引くのを思い出してください。最近はあまり目にしなくなりましたが、紙の辞書です。

「でんわ」という単語を探すとき、

1. 真ん中あたりをテキトーに開く
2. 「セールス」のページだったので、少し後ろを開く
3. 「トーク」のページだったので、少し前を開く
   と繰り返し、最終的に「でんわ」のページにたどり着くと思います。

1ページ目から順にめくったりしないですよね？

辞書引きでは、辞書全体の大体真ん中にあるだろう。というところからスタートし、雑に開いた後は、今のページより前の方にあるか後ろの方にあるかを確認することで「でんわ」が載っている範囲を絞り込みました。
配列から数字を探すのも同じです。テキトーに真ん中あたりを調べて、数値の大小によって前半にあるか、後半にあるかを絞り込んでいきます。

二分探索を利用して添字探しを実装するとこんな感じになります。

left = 0 # 配列の先頭の添字
right = N # 配列の末尾の次の添字
while left < right:
    mid = (left + right) // 2 # 現在の探索範囲の真ん中の添字
    if A[mid] < X:
        # 確認したところが X より小さい => X は確認したところより大きい側にある
        left = mid # 探索範囲を狭める
    elif A[mid] > X:
        # 確認したところが X より大きい => X は確認したところより小さい側にある
        right = mid # 探索範囲を狭める
    else:
        print(f'index: {mid}')
        break

実行時間は 線形探索と二分探索の実行時間の比較 のようになります。
少し複雑になりましたが、この方法だと配列の長さが長くなっても高速に調べることができます。

注意点は事前にソートする必要があることです。大小関係の比較により範囲を絞り込んでいくので、ソート済みでないとおかしなことが起こります。
辞書の時はソートされている前提があったので、特に気にしてませんでした。

一例として「配列内にある値の添字を探す」問題を取り上げましたが、二分探索の応用範囲は広く、「ソートされているものから何かを探す」場合には適用できることが多いです。

RevComm での応用

「配列の中で欠けている複数の番号の中で一番最小のものを求めよ」

内線電話

弊社で開発している MiiTel Analytics は解析機能のついた電話のサービスです。
スマホのように遠くにいる人と通話する外線通話の他に、会社や学校のように 1つの組織内で利用する内線通話という機能があります。
内線通話には外線通話とは別の電話番号を利用します。(グローバル IP とプライベート IP みたいなもんですね)
通常、電話番号というと 080, 0120, 03 などから始まるユニークな番号ですが、内線番号は組織内でユニークであれば、外部の組織とはかぶっていても問題ありません。

内線番号の発番

MiiTel Analytics は会社のような組織が利用することを想定した設計になっており、1つのグループに複数のユーザを作成することができます。
内線番号はユーザを新規作成したタイミングで発番されます。作成後、ユーザは自分の内線番号を (グループ内でユニークな範囲で) 自由に変更できるので、次にユーザ作成する時にはどの内線番号が空いているかを確認する必要があります。

MiiTel Analytics では、空いている番号のうち最小のものを初期値として設定しています。¹
さて、ソート済みの使用中の内線番号が与えられたとして、新規作成するユーザの内線番号はどのように求めれば良いでしょうか。

方針1: 使われている番号を線形探索する

• 次の番号との差がちょうど 1 かどうかを確認し、空いている番号を求める
• 前から順に調べる

# used_internal_numbers: 使用中の内線番号
# initial_internal_number: 求めた内線番号の初期値
N = len(used_internal_numbers)

if N == 0:
    # 使用中の番号なし
    initial_internal_number = 0
elif N == 1 and used_internal_numbers[0] == 0:
    # 使用中の番号は 0 のみ
    initial_internal_number = 1
elif used_internal_numbers[0] > 0:
    # 最小の番号が使える
    initial_internal_number = 0
else:
    for i in range(N-1):
        if used_internal_numbers[i] + 1 < used_internal_numbers[i+1]:
            initial_internal_number = used_internal_numbers[i] + 1
            break
    else:
        # 使用中の番号は連続
        initial_internal_number = used_internal_numbers[-1] + 1

方針2: 使われている番号を二分探索する

• i と used_internal_numbers[i] の差は単調非減少で、使われてない番号までは 0 が続くことを利用する
• used_internal_numbers[i] - i を 1つの配列とみなし、初めて 0 より大きくなる i (used_internal_numbers[i]) を二分探索によって求める

# used_internal_numbers: 使用中の内線番号
# initial_internal_number: 求めた内線番号の初期値
N = len(used_internal_numbers)

if N == 0:
    # 使用中の番号なし
    initial_internal_number = 0
elif N == 1 and used_internal_numbers[0] == 0:
    # 使用中の番号は 0 のみ
    initial_internal_number = 1
elif used_internal_numbers[0] > 0:
    # 最小の番号が使える
    initial_internal_number = 0
else:
    # left: ぎりぎり差が 0 の添字
    # right: ぎりぎり差が 0 より大きくなる添字
    # となるように二分探索する
    left = 0
    right = N
    while left + 1 < right:
        mid = (left + right) // 2
        if used_internal_numbers[mid] - mid == 0:
            # 差が 0 なら、境目は大きいところにある
            left = mid
        elif used_internal_numbers[mid] - mid > 0:
            # 差が 0 より大きいなら、境目は小さいところにある
            right = mid
    initial_internal_number = used_internal_numbers[left] + 1

方針3: 使われてない番号の一覧を求める

• 使用中番号の最大値までの範囲で使われてない番号の一覧を求める
• 使われてない番号があればその最小値、なければ 使われている番号の最大値 + 1

# used_internal_numbers: 使用中の内線番号
# initial_internal_number: 求めた内線番号の初期値
free_internal_numbers = set(range(used_internal_numbers[-1])) - set(used_internal_numbers) # 使われてない番号一覧
if len(free_internal_numbers) == 0:
    # 使われている番号が連続している場合
    initial_internal_number = used_internal_numbers[-1] + 1
else:
    initial_internal_number = min(free_internal_numbers)

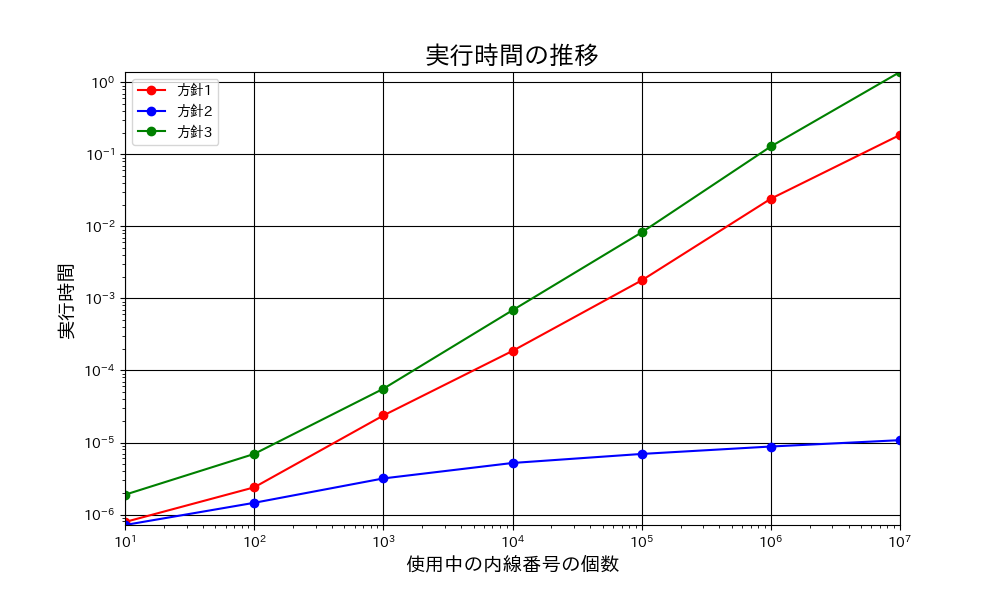
各方針の実行時間の比較

今回作成したテストケースは少々作為的ですが、方針1 や方針3 と比較して方針2 は高速なのが分かります。
内線番号の個数の最大値は約 $ 10^{9} $ 個ですが、実用の範囲では線形探索でも十分高速なので、よりシンプルな実装の方がいいんじゃないかと思ったりもします。
ただレスポンス速度は UX に直結するため、より速い方を採用しています。

最後に

最後まで読んでいただきありがとうございました。
このタスクは私が RevComm に入社した頃に @series さんから振られたもので、思い出深いものです。競プロのこと知らないと言ってたのにこの形式で出てきたことにびっくりしたのを覚えています。

「配列の中で欠けている複数の番号の中で一番最小のものを求めよ」

本記事では RevComm の裏側で動くアルゴリズムと題して二分探索を紹介しました。
探索アルゴリズムの中には「三分探索」なるものもあります。それについてはまた次回紹介しましょう。

明日は @kyogom さんの 「ファイルシステムをCase-sensitiveに設定しておこう for Mac」 です。

1. 他にもありますが今回はこの条件にしておきます。また、頭に0がつく番号は考慮せず、整数値として扱いました。 ↩