Shorのアルゴリズムを解説してみた

はじめに

本記事では素因数分解問題の多項式時間アルゴリズムとして有名な、Shorのアルゴリズムをできるだけ分かりやすく解説します。私（量子ゲート歴1年未満の素人）がShorのアルゴリズムを理解するときに詰まったポイントについて少し深堀りながら説明を行っていきます。必要とあらば（少なくとも私には必要でした）量子や数学の基礎から振り返っていきます。

なお、本記事はまだまだ「完全に理解した」状態である筆者が書いたものです。内容に誤りが含まれる可能性がありますので予めご容赦下さい。ぜひコメント等でご指摘いただけますと幸いです。
より専門的な解説は、偉大な先人の書籍・記事をご覧下さい。本記事はそんな先人の説明さえ理解できなかった過去の私に向けた記事です。

• 『量子コンピューティング: 基本アルゴリズムから量子機械学習まで』嶋田
• 『量子コンピュータ入門(第2版)』宮野、古澤
• ショアのアルゴリズム(Qiskitテキストブック)
• Shorのアルゴリズム(gyu-don)

$$ \def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} \def\coloneqq{\mathrel{\mathop:}=} $$

冪剰余

早速Shorのアルゴリズムを説明していきたいところですが、このアルゴリズムを理解するためには冪剰余について知っておく必要があります。

f(x)_{a,N} = a^x\bmod N

整数$N$、定数$a$が与えられたとき、$a$の冪乗を$N$で割った余りを冪剰余と呼びます。この数式には一方向性があり、$x$から$f(x)$を求めるのは容易ですが$f(x)$から$x$を求めるのは一般に困難とされています。$f(x)$から$x$を求める問題を離散対数問題と呼び、暗号技術の基礎として活用されています。厳密には離散対数問題の一例らしいのですが、取っ付きやすさから冪剰余を元にした説明が多く見かけられます^{1 2}。

この冪剰余には「$x$を1ずつ増やすと、$f(x)$が周期的に変化する」という面白い性質があります。$N=35$、$a=2$ の場合で眺めてみましょう。

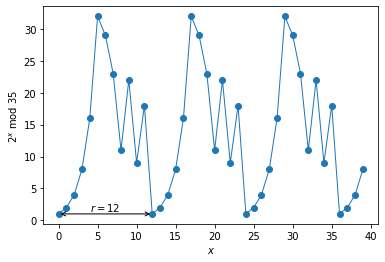
このように12を1サイクルとして周期的に変化していることが分かります。この波長を位数と呼び、以降$r$で表記します。また、冪剰余を段階的に求めるために剰余乗算が使われることもあります。
$$g(y)_{a,N} = y \cdot a \bmod N$$

\begin{align}
g^{x-1}(a)_{a,N} &= a^x\bmod N \\
&= f(x)_{a,N}
\end{align}

次の章からはこの冪剰余を活用してShorのアルゴリズムの理解を進めていきます。

Shorのアルゴリズム

Shorのアルゴリズムは一言で言えば、素因数分解の古典アルゴリズムのサブルーチン部分（冪剰余の位数発見問題）を量子計算で代替したアルゴリズム、と説明できます。
Shorのアルゴリズムが着目する素因数分解アルゴリズムは以下の通りです。

1. 素因数分解したい整数$N$と互いに素な整数$a(<N)$を用意する。
2. $N$を法とする$a$の冪剰余 $f(x)_{a,N} = a^x\bmod N$ の位数$r$を見つける。
3. $r$が奇数ならばステップ1へ戻る。
4. $\gcd(a^{r/2}+1,N)$と$\gcd(a^{r/2}-1,N)$を計算すると、$N$の素因数が得られる。

ステップ2に示した位数発見問題は古典計算で解くことも可能です。ですが2021年現在、位数発見問題を多項式時間で解く古典アルゴリズムは存在しません。Shorのアルゴリズムの見どころは、位数発見問題を量子計算で短縮するところです。そのため本記事では以降、冪剰余の位数発見問題について重点的に解説します。

なお、ステップ1では$\gcd(a,N)=1$となる$a$を用意すれば良く、位数発見問題以外は$\gcd()$が主要な計算対象です。$\gcd()$はユークリッドの互除法によって$O(\log N)$で計算できることが知られています。位数発見問題の高速化がアルゴリズム全体の高速化につながるという訳です。

冪剰余は周期をもつのか

ところで、すべての冪剰余は本当に周期を持つのでしょうか。すべてでは無いものの、Shorのアルゴリズムが着目する冪剰余は特定の周期を有するようです³。
感覚的な説明になりますが以下。

• $N$を法とする整数は$[0, N-1]$の範囲に収まっている。
• もっというと割り切れる$a^x$は取らないため、$[1, N-1]$の範囲に収まっている。
• $a^x \bmod N$から$a^{x+1} \bmod N$への遷移が必ず異なる値になるため、いずれ$a^x \bmod N =　a^{x+r} \bmod N $となる$r$が見つかる。

量子計算による位数発見

それでは、量子計算を用いて位数発見問題を解く方法を見ていきましょう。
Shorが提案した位数発見手法は一言で言えば、剰余乗算回路$U_{a,N}$と「かしこい」固有ベクトルを用意して固有値を求める手法、と説明できます。求めた固有値が位数$r$の情報を含むため、最後に位数を取り出す手順も必要となっています。

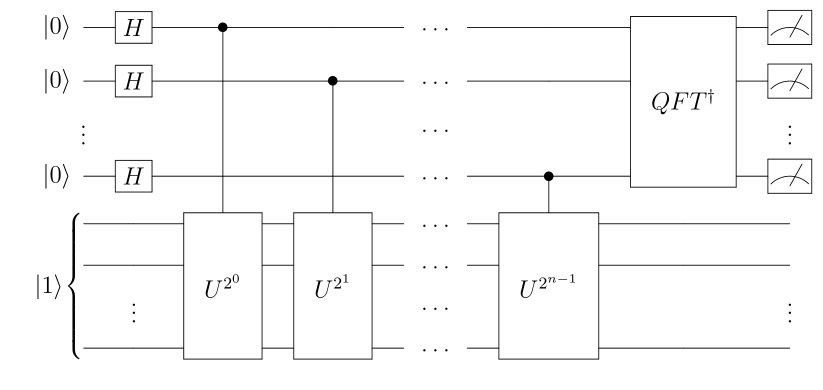
これが位数発見を行う量子回路です。大枠は量子位相推定であり、量子位相推定回路に剰余乗算回路$U_{a,N}$と$\ket{1}$を設定するのが重要なポイントです。

量子位相推定はユニタリ行列と固有ベクトルを与えると固有値の位相を求めてくれます。今回のアドベントカレンダーでも紹介していますので、詳細はこちらの記事をご覧ください。

ちなみに、量子位相推定はこちらもこちらで理解が難しかった印象があるので、次の事実を抑えてから理解を進めることをおすすめします。

• 量子ゲート操作はユニタリ行列で表現できる。
• ユニタリ行列の固有値の絶対値は1となる⁴。つまり固有値は$e^{i2\pi\phi}$（$0\leq\phi\lt1$）の形式で表現できる。$\phi$を位相という。
• 量子回路の表記法は不完全である。位相キックバックによって制御〇〇ゲートの制御ビットは変化することがある。

剰余乗算演算

まずは、剰余乗算演算をユニタリ行列としてどう表現するか見てみましょう。

U_{a,N} \ket{y} = \ket{y \cdot a\bmod N}

ブラケット記法ではこのような変換として表すことができます。。できるんですが、多くの方々がこの数式やこの後の固有値の導出に苦しんでいる姿が目に浮かんできました。Shorのアルゴリズムが有名すぎる所為か、これまでパウリゲートやアダマールゲートぐらいしか見たことない方々（過去の私）でも、いきなりShorに出会っているのではないでしょうか。ともあれそんな方々を救うために一旦、ブラケット記法の基底エンコーディングと基底エンコード中の演算について説明を挟みます（もちろん量子位相推定も理解しておく必要があるので、初学者はいますぐ引き返してください！）。

基底エンコーディング

基底エンコーディングとは、10進数を量子ビット列（基底ベクトル）に対応づけることを指します。4量子ビットを扱う場合、次のように対応付けられます。

\ket{0} \coloneqq \ket{0000}, \ket{1} \coloneqq \ket{0001}, \ket{2} \coloneqq \ket{0010}, \ket{3} \coloneqq \ket{0011}, \ldots

また、エンコード済みのブラケット記法では、ケットの外側と内側で記号の意味が異なります。例えば、+記号はケットの外側では重ね合わせ状態を意味します。

\ket{\psi} = \frac{1}{\sqrt{2}}(\ket{3} + \ket{4})

一方、+記号はケットの内側では足し算を意味します。4を加算する量子回路を$A_4$とすると、
$$A_4\ket{3} = \ket{3+4} = \ket{7}$$

A_4\ket{\psi} = \frac{1}{\sqrt{2}}(\ket{3+4} + \ket{4+4}) = \frac{1}{\sqrt{2}}(\ket{7} + \ket{8})

なお、エンコード済みの$\ket{0}$と$\ket{1}$は、1量子ビットの基底ベクトルと間違いやすいので注意してください。違いが分かるように、1量子ビットの基底ベクトルを太字で$\ket{\mathbf{0}}$と$\ket{\mathbf{1}}$と表記すると、4量子ビットは次のように対応付けられます。

\ket{0} \coloneqq \ket{\mathbf{0}}\otimes\ket{\mathbf{0}}\otimes\ket{\mathbf{0}}\otimes\ket{\mathbf{0}}, \ket{1} \coloneqq \ket{\mathbf{0}}\otimes\ket{\mathbf{0}}\otimes\ket{\mathbf{0}}\otimes\ket{\mathbf{1}}, \ldots

また、数式を扱うときはあまり意識しませんが、$n$個の量子ビットでエンコード可能な数は$\ket{0}$から$\ket{2^n -1}$までです。いざ量子回路に乗せたときに$2^n$以上の数値を扱ってしまうとバグるため注意が必要です。

再チャレンジ：剰余乗算演算

基底エンコーディングを理解したのでもう一度、剰余乗算演算を見てみましょう。ケットの中身はエンコード済みです。

U_{a,N} \ket{y} = \ket{y \cdot a\bmod N}

ぱっと見、このような量子回路を組めるのか疑問に思われるかもしれません。お察しのとおり、剰余乗算回路を作るにはある程度手間がかかります⁵。しかし作れることは確かです。
以下の論文などで剰余乗算回路を組むための研究がなされています。我々は彼らの功績に感謝しつつ、Shorのアルゴリズムの理解を進めましょう。

• V. Vedral, A. Barenco and A. Ekert(1995), "Quantum Networks for Elementary Arithmetic Operations"
• S. Beauregard(2003), "Circuit for Shor’s algorithm using 2n+3 qubits"

さて剰余乗算回路が用意できることが分かったので、次は剰余乗算演算の固有値、固有ベクトルについて見ていきましょう。興味深いことに剰余乗算演算の固有値、固有ベクトルは、位数$r$を含む形となっています。

$r$個の固有値はそれぞれ以下のとおりであり、

e^{i2\pi\frac{s}{r}} \quad (s=0,1,\ldots,r-1)

固有値に対応する固有ベクトルはそれぞれ以下のとおりです。

\ket{u_s} = \frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}e^{-i2\pi\frac{s}{r}j}\ket{a^j \bmod N} \quad (s=0,1,\ldots,r-1)

細かな導出はQiskitテキストブックに譲ります。具体例が多くて分かりやすいです。

「かしこい」固有ベクトル

さて固有ベクトルが明らかになったものの、まだ位数$r$が分からないためこのままでは固有ベクトルを用意することはできません。そこで考え出されたのが固有ベクトルの重ね合わせ状態でした。不思議なことに固有ベクトルの重ね合わせは$\ket{1}$になります。

\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s} = \ket{1}

量子計算では重ね合わせ状態を入力すると、重ね合わせ状態で結果が返ってきます。
つまり$\ket{1}$について量子位相推定を行うと、固有値の位相$s/r$の重ね合わせ状態が得られます。

求めた固有値（位相）から位数を取り出す

最後に、得られた位相$s/r$の重ね合わせ状態から位数$r$を取り出す方法を説明します。
まず$N=35$、$a=2$ の場合で考えると、位相$s/r$の重ね合わせ状態から測定される値はこのようになります。

0,\frac{1}{12},\frac{2}{12},\frac{3}{12},\frac{4}{12},\frac{5}{12},\frac{6}{12},\frac{7}{12},\frac{8}{12},\frac{9}{12},\frac{10}{12},\frac{11}{12}

実際には$r=12$を知りえないので、測定結果を次のように捉えるはずです。

0,\frac{1}{12},\frac{1}{6},\frac{1}{4},\frac{1}{3},\frac{5}{12},\frac{1}{2},\frac{7}{12},\frac{2}{3},\frac{3}{4},\frac{5}{6},\frac{11}{12}

$s/r = 0$が得られた場合は再度測定します。$r = 2,3,4,6$が得られた場合も$2^r \bmod 35 = 1$を満たさないため再度測定します。$r = 12$が得られた場合は見事位数を発見したことになります。測定し直しが多いと思われるかもしれませんが、$x$から$a^x \bmod N$を求める検算は容易であるため、比較的やり直しが容易です。

ただし素直に位数を求められない場合には、連分数展開をもちいて$s/r$の近似値を利用します⁶。例えば、量子位相推定の出力結果が10量子ビットで返ってきたとすると、$\ket{0/2^{10}}$から$\ket{1023/2^{10}}$までの値を取りえます。$s/r = 1/12$の状態は、$85/1024$などのように測定されます。

連分数展開はこのようになるので、

85/1024 = \frac{1}{12+\frac{1}{21+\frac{1}{4}}}

$s/r$の近似精度を徐々にあげながら、$1/12$、$1/253$、$85/1024$といった具合に$r$を探すことが可能です。

まとめ

ここまでの話をまとめると、量子計算による位数発見手法は以下の通りとなります。

1. 与えられた整数$N$と$a$から剰余乗算回路$U_{a,N}$を用意する。
2. 固有ベクトルに$\ket{1}$を、制御ユニタリ行列に$U_{a,N}$を設定し量子位相推定を行う。
3. 得られた結果$s/r = 0$ならばステップ2へ戻る。
4. $s/r$から$r$を取り出し、$a^r \bmod N = 1$を満たすならば終了、満たさないならばステップ2へ戻る。

以上で解説を終わります。皆さんの量子勉強の足しになればと思います。

1. https://hazm.at/mox/security/public-key/discrete-logarithm-problem/index.html ↩

2. http://herumi.in.coocan.jp/crypt/crypt01.html ↩

3. https://speakerdeck.com/gyudon/shorfalsearugorizumu?slide=5! の注釈 ↩

4. https://ja.wikipedia.org/wiki/%E3%83%A6%E3%83%8B%E3%82%BF%E3%83%AA%E8%A1%8C%E5%88%97 ↩

5. https://qiita.com/SamN/items/fc350338c2222561488b ↩

6. https://ja.wikipedia.org/wiki/%E3%83%87%E3%82%A3%E3%82%AA%E3%83%95%E3%82%A1%E3%83%B3%E3%83%88%E3%82%B9%E8%BF%91%E4%BC%BC#%E3%83%87%E3%82%A3%E3%83%AA%E3%82%AF%E3%83%AC%E3%81%AE%E5%AE%9A%E7%90%86 に一部記載あり。連分数展開はユークリッドの互除法と同様の手順で導出可能。 ↩