Qiskit pulseを用いて状態操作

前回，Qutipでpulse操作のシミュレーションを行ったので，今回はQiskitを用いて実際にパルス操作を行なってみたいと思います．参考にした文献は最後に記しました．

qiskit pulse

まず，ガウシアンパルスの振幅の設定（前回の$\Omega(t)$に対応）を行います．

from qiskit import IBMQ
import numpy as np
from qiskit import pulse                  
from qiskit.circuit import Parameter      
from qiskit.circuit import QuantumCircuit, Gate


#IBMQ.save_account("") # 最初はtokenの入力が必要
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('') # 使えるbackendを選んでください

backend_config = backend.configuration()
backend_defaults = backend.defaults()

GHz = 1.0e9 # Gigahertz
MHz = 1.0e6 # Megahertz
us = 1.0e-6 # Microseconds
ns = 1.0e-9 # Nanoseconds

dt = backend_config.dt
print(f"Sampling time: {dt * 1e9} ns") 
# Sampling time: 0.5 ns

granularity = backend_config.timing_constraints['granularity']
print(granularity)
# 8

# value を base_number の倍数に丸める関数
def get_closest_multiple_of(vaule, base_number):
    return int(vaule + base_number/2) - (int(vaule + base_number/2) % base_number)

# num を granularity の倍数に丸める関数
def get_closest_multiple_of_granu(num):
    return get_closest_multiple_of(num, granularity)


# ガウシアンパルスのパラメータ
drive_sigma_sec = 15 * ns  # ガウシアンの幅
drive_duration_sec = 120 * ns  # 全体の時間幅
drive_amp = 0.05 #振幅

ここで，granularityは「時間粒度」，つまり操作できる最小の単位時間を表しています．上記の例だと，sampling timeが$0.5\mathrm{ns}$であり，これが粒度の単位になっています．今回 granularity$=8$なので，時間粒度は$4\mathrm{ns}$となります．全ての操作は$4\mathrm{ns}$の倍数の時間で操作しなければなりません．よって，

# ベーススケジュールを作成
freq = Parameter('freq')
with pulse.build(backend=backend, default_alignment='sequential', name='Frequency sweep') as sweep_sched:
    drive_duration = get_closest_multiple_of_granu(pulse.seconds_to_samples(drive_duration_sec))
    drive_sigma = pulse.seconds_to_samples(drive_sigma_sec)
    drive_chan = pulse.drive_channel(qubit)
    pulse.set_frequency(freq, drive_chan)
    # Drive pulse samples
    pulse.play(pulse.Gaussian(duration=drive_duration,
                              sigma=drive_sigma,
                              amp=drive_amp,
                              name='freq_sweep_excitation_pulse'), drive_chan)

のようにガウシアンパルスを設定すると，以下のような，$4$nsの倍数の時間だけ作用するパルスを作ることができます．

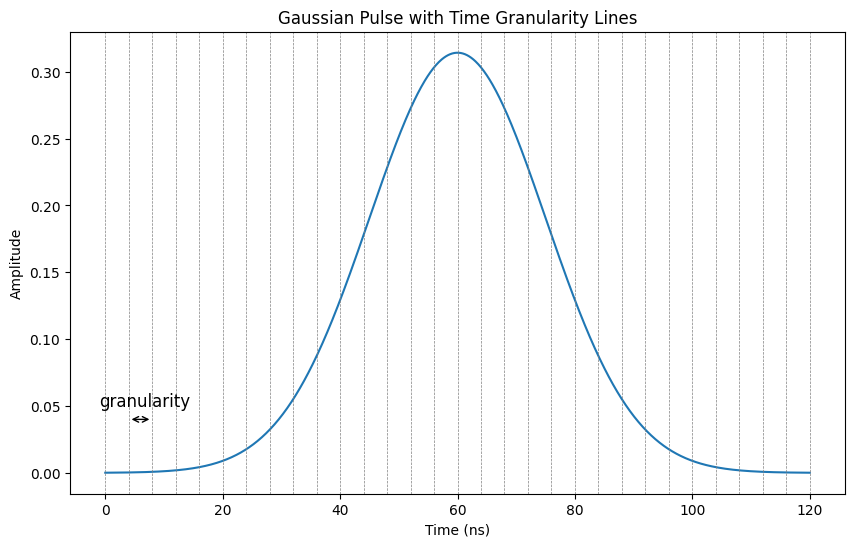
ちなみに，seconds_to_samplesでは，秒で与えた時間を，サンプル数に変換しています．例えば，全体の時間幅は$120\mathrm{ns}$なので，サンプル数は$240$となっています（sampling timeが$0.5\mathrm{ns}$）¹．

さて，次にガウシアンパルスの周波数（前回の$\omega_d$に対応）の設定を行います．ここでは，量子ビットのエネルギー差に対応する周波数$\omega_q$のおおよその値が与えられており，パルスの周波数$\omega_d$を量子ビットの周波数$\omega_q$周辺で変化させていくことにより，測定結果がどのように変わるかを見ていきます．

# 周波数を探索する量子ビット
qubit = 0

# デフォルトの推定周波数を中心値としてスイープを行う
center_frequency_Hz = backend_defaults.qubit_freq_est[qubit] 
print(f"量子ビット {qubit} の推定周波数は {center_frequency_Hz / GHz} GHz")
#量子ビット 0 の推定周波数は 4.908828173067439 GHz

# 推定周波数を中心に100MHzの間でスイープする
frequency_span_Hz = 100 * MHz
frequency_step_Hz = 1 * MHz
frequency_min = center_frequency_Hz - frequency_span_Hz / 2
frequency_max = center_frequency_Hz + frequency_span_Hz / 2

# 周波数の配列をGHz単位で作成
frequencies_GHz = np.arange(frequency_min / GHz,
                            frequency_max / GHz,
                            frequency_step_Hz / GHz)
print(f"スイープは {frequency_min / GHz} GHz から {frequency_max / GHz} GHz まで、{frequency_step_Hz / MHz} MHz のステップで行われる")
#スイープは 4.858828173067439 GHz から 4.958828173067439 GHz まで、1.0 MHz のステップで行われる

これで準備は全て終わりました．ガウシアンパルスのゲートを作り，それを作用させていきます．

sweep_gate = Gate("sweep", 1, [freq]) #"1"は1量子ビットゲートという意味

qc_sweep = QuantumCircuit(1, 1)
qc_sweep.append(sweep_gate, [0])
qc_sweep.measure(0, 0)
qc_sweep.add_calibration(sweep_gate, (0,), sweep_sched, [freq])

frequencies_Hz = frequencies_GHz*GHz
exp_sweep_circs = [qc_sweep.assign_parameters({freq: f}, inplace=False) for f in frequencies_Hz]

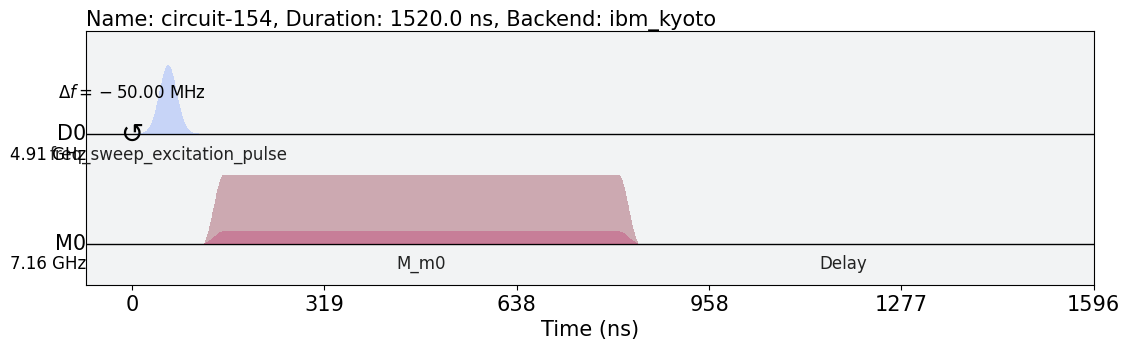
このスケジュールを図示すると，次のようになります．

from qiskit import schedule

sweep_schedule = schedule(exp_sweep_circs[0], backend)
sweep_schedule.draw(backend=backend)

これを実行してみます．

import matplotlib.pyplot as plt

num_shots_per_frequency = 1024

job = backend.run(exp_sweep_circs,
                  meas_level=1,
                  meas_return='avg',
                  shots=num_shots_per_frequency)

# 結果
frequency_sweep_results = job.result(timeout=120) 

# データを見やすくするスケーリング
scale_factor = 1e-7

sweep_values = []
for i in range(len(frequency_sweep_results.results)):
    #　i番目の周波数での実験結果
    res = frequency_sweep_results.get_memory(i)*scale_factor
    sweep_values.append(res[qubit])

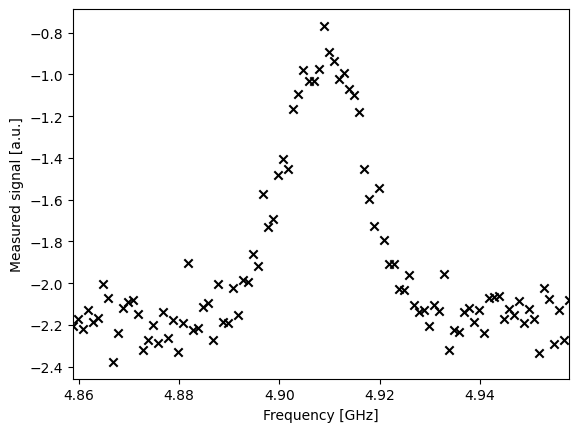
plt.scatter(frequencies_GHz, np.real(sweep_values), marker='x', color='black') # plot real part of sweep values
plt.xlim([min(frequencies_GHz), max(frequencies_GHz)])
plt.xlabel("Frequency [GHz]")
plt.ylabel("Measured signal [a.u.]")
plt.show()

前回のシミュレーション結果と似たような結果が得られました．

参考文献

• QiskitのOpenPulseでパルス制御【共鳴周波数の測定】
• Qiskit Pulseによる量子ビットの較正

1. 振幅はdrive_amp=0.05としましたが，これの単位が不明なため，シミュレーション結果とどの程度一致するのかどうかは分かりません． ↩