Qutipで量子ビットのパルス操作シミュレーション

Qiskitのパルスで遊ぶ前に，２準位系のシミュレーションをQutipを用いて行います．

様々な近似後の量子ビット

量子コンピュータは量子ビットから成り立っていますが，例えば超伝導量子ビットは，物理的には２準位系ではなく，多準位系となっています．２準位系として扱うためにJJを加え非線形性を加え，様々な近似を適用し，その低準位だけに着目することによって２準位系として扱えます¹．ここでは，その２準位系のシミュレーションを行います．

さて，ここでは次の２準位系を考えます．
$$
\begin{align}
H(t)=-\frac{1}{2} \hbar (\omega_q-\omega_d) \sigma^z-\hbar \Omega(t) \sigma^x
\end{align}
$$

ここで，$\hbar\omega_q$がtransmonの基底エネルギーと第１励起エネルギーの差，$\omega_d$が加えるマイクロ波の角周波数，$\hbar\Omega(t)$が加えるマイクロ波とtransmonの双極子相互作用の大きさを表しています．最後の項が時間に依存しているのは，マイクロ波の振幅が時間に依存していることを表しています．

マイクロ波の波形

マイクロ波の波形は，Qiskitではいくつか指定できます．代表的なものを以下に紹介します．

$$
\begin{aligned}
\text{Constant: }&\hbar\Omega(t)=
\begin{cases}
A \exp (i \theta)& 0\leq t<T \\
0& \text { others }
\end{cases}\\
\text{Gaussian: }&\hbar\Omega(t)=
\begin{cases}
A \frac{f(t)-f(-1)}{1-f(-1)}& 0\leq t<T \\
0& \text { others }
\end{cases}\\
& \quad f(t)= \exp \left(-\frac{1}{2} \frac{(t-\frac{T}{2})^2}{\sigma^2}\right)\\
\text{Gaussian square: }&\hbar\Omega(t)=
\begin{cases}
A \frac{g(t)-g(-1)}{1-g(-1)}& 0\leq t<T \\
0& \text { others }
\end{cases}\\
& \quad g(t)=
\begin{cases}
\exp \left(-\frac{1}{2} \frac{(t-\frac{T-w}{2})^2}{\sigma^2}\right)& 0\leq t<\frac{T-w}{2} \\
1& \frac{T-w}{2}\leq t<\frac{T+w}{2} \\
\exp \left(-\frac{1}{2} \frac{(t-\frac{T+w}{2})^2}{\sigma^2}\right)&\frac{T+w}{2}\leq t<T
\end{cases}
\end{aligned}
$$
これらは以下のような波形になっています．

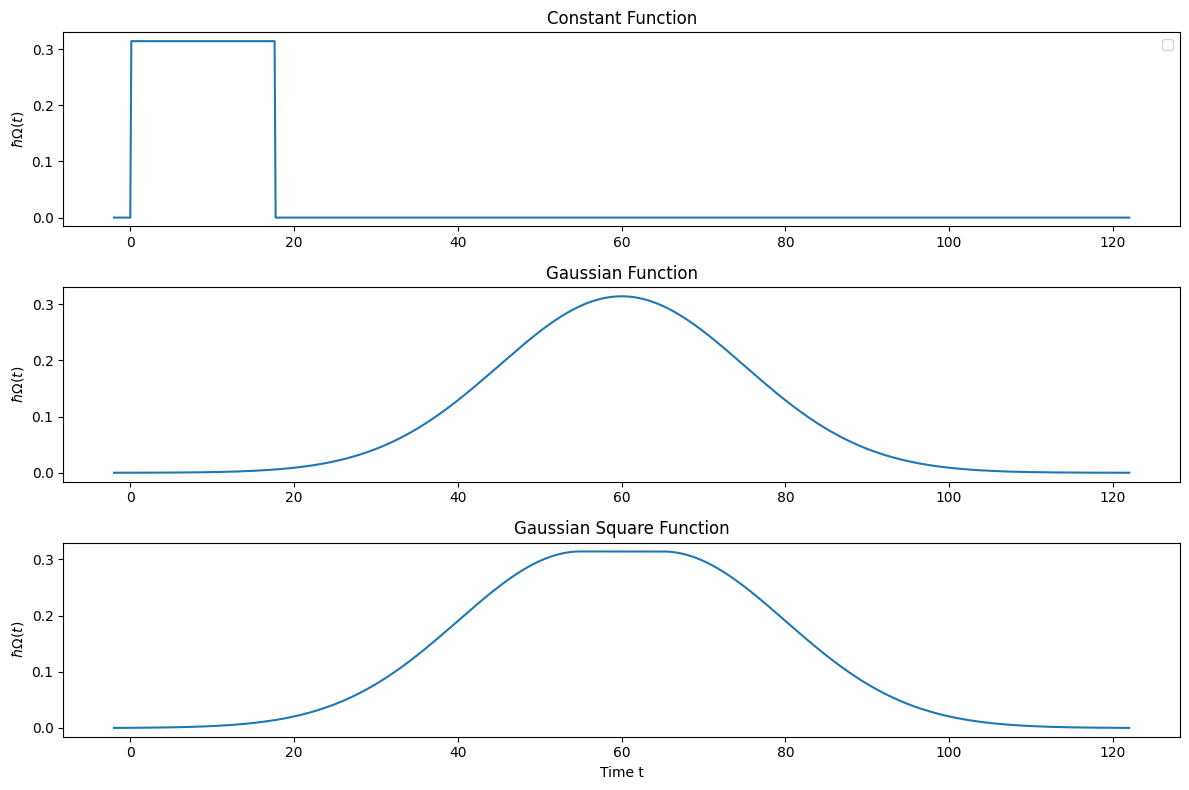
ここで，Constant pulseにおける$T$は，Gaussian pulseのHWHMとしました．

他にもいろいろあるので，ぜひ見てみてください．

Qutipでシミュレーション

次にConstant pulseとGaussian pulseを用いて，Qutipでシミュレーションします．Qutipでは

$$
\begin{align}
i\frac{d}{dt}\ket{\psi(t)}&=\frac{H(t)}{\hbar}\ket{\psi(t)}\\
&=\left(-\frac{1}{2} (\omega_q-\omega_d) \sigma^z- \Omega(t) \sigma^x\right)\ket{\psi(t)}
\end{align}
$$

をsesolveでシミュレートできます．この最後の右辺をハミルトニアンとして定義し，シミュレートしてみましょう．

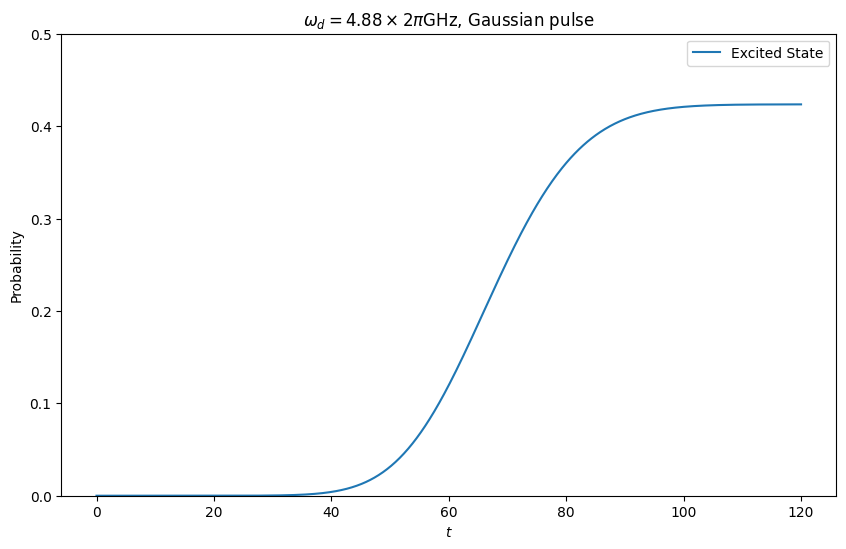
以下，$\omega_q=4.91\times 2\pi \mathrm{GHz}, \ \Omega(t)\leq 0.05\times 2\pi \mathrm{GHz}, \ \sigma = 15\mathrm{ns}$とします．また，まずは$\omega_d=4.88\times 2\pi \mathrm{GHz}$としてみましょう．

from qutip import basis, sesolve, sigmax, sigmaz
import numpy as np

# 角周波数
omega_q = 4.91 * 2 * np.pi
omega_d = 4.88 * 2 * np.pi
Delta_q = omega_q - omega_d # [GHz]

# Hamiltonian
H0 = - Delta_q * sigmaz() / 2 

# 時間の設定
time_steps = 1000
T0 = 120
times = np.linspace(0, T0, time_steps) # [ns]


# 初期状態 (基底状態)
psi0 = basis(2, 0)

# Gaussian pulse
def gaussian_pulse(t, args):
    amp = args['amp'] # [1/ns]
    sigma = args['sigma'] # [ns]
    center = args['center']
    return amp * np.exp(-(t - center) ** 2 / (2 * sigma ** 2))

# Gaussian pulse parameters
gaussian_args = {'amp': 0.003 * np.pi * 2, 'sigma': 15.0, 'center': times[time_steps // 2]}

# 時間依存Hamiltonian
H = [H0, [-sigmax(), gaussian_pulse]]

# Simulation
result = sesolve(H, psi0, times, e_ops=[], args=gaussian_args)

# 結果
final_state = result.states[-1]
ground_state_probabilities = [abs(state[1, 0])**2 for state in result.states]

例えばGaussian pulseの場合，初期状態を$\ket{0}$とした際の$\ket{1}$に遷移する確率は次のような時間依存性を持ちます．

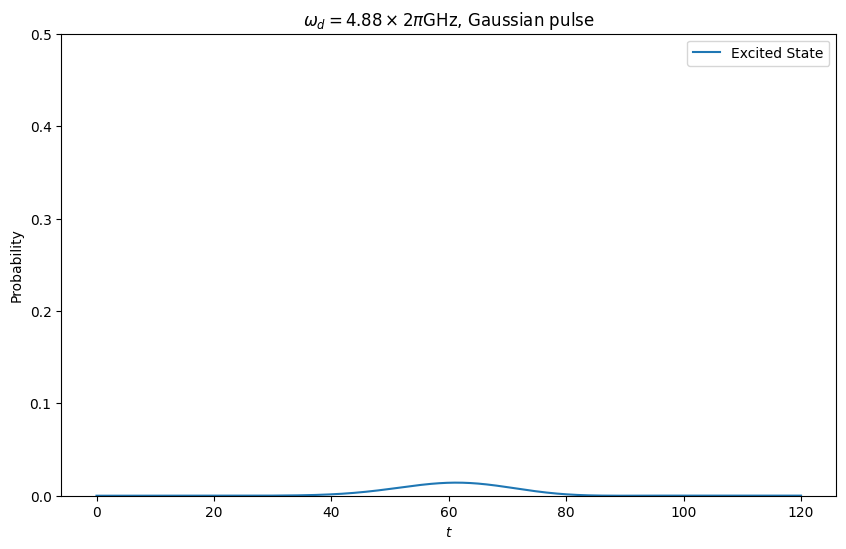
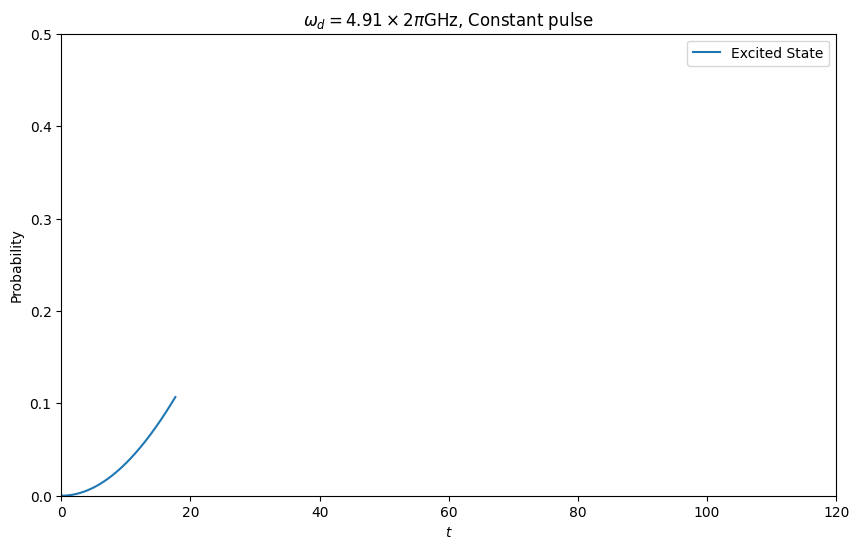
一方，Constant pulseの場合，次のような時間発展を示します．

また，共鳴している場合は，

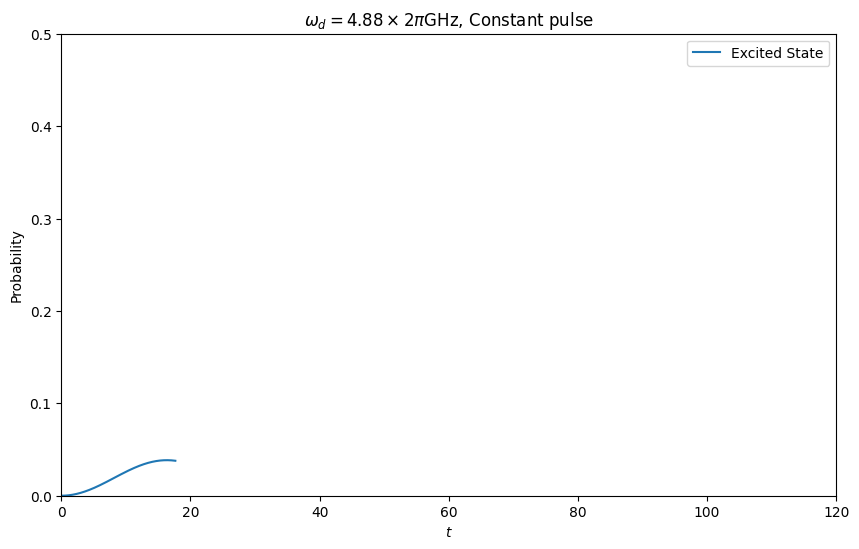
となります．

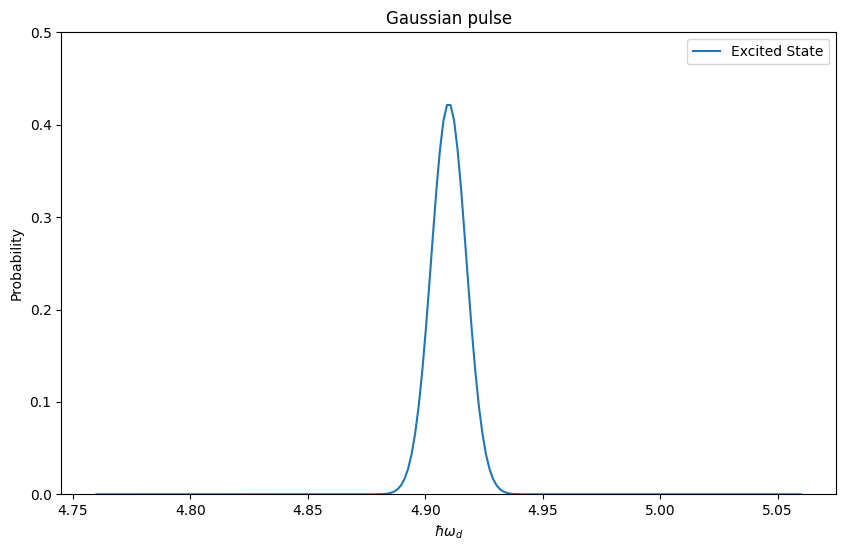
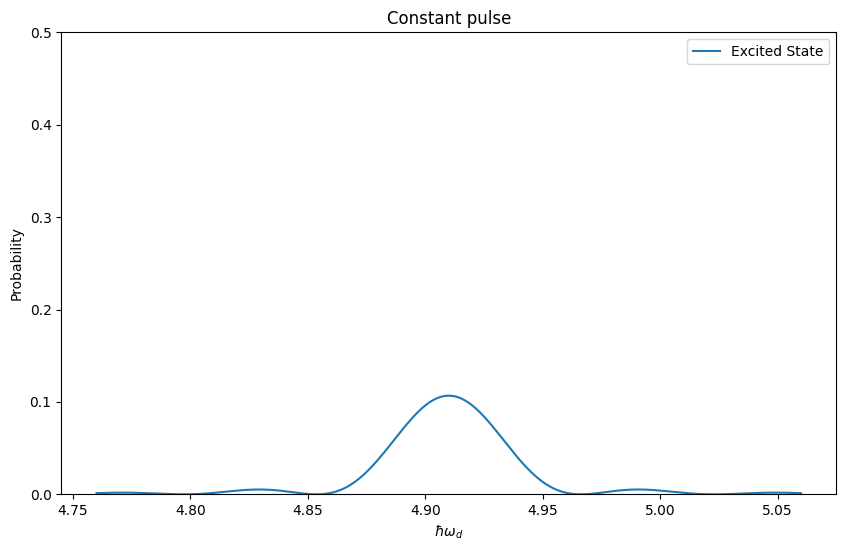
様々な$\omega_d$についてプロットしたのが以下の図です．

Gaussian pulseでは共鳴しているときに特異な振る舞いを示すのに対し，Constant pulseでは，その前後でも励起される確率があることが分かります．これより，$\omega_p$を求めたい場合にはGaussian pulseを用いると良いことが分かりました．

なぜGaussianは共鳴の際のみ遷移が起きるのか

共鳴していない場合のGaussian pulseにおける遷移確率の図を見てもらうと，これもGaussianに似た振る舞いになっていることが分かります．これより，断熱的な過程になっていることが推測できます²．しかし，共鳴条件を満たしている場合は，断熱条件を満たしていたとしても断熱過程にならないことが知られています．この性質をうまく利用した結果と言えるでしょう．

Appendix: 解析的な計算

Constant pulseの場合は解析的な計算が可能なので，気が向いた時に計算しようと思います．

1. これについては今後詳しく説明するつもりです． ↩

2. 断熱条件を満たしているかどうかは時間があったら確認します． ↩