はじめに
こんにちは!
僕は研究を行いながら、長期インターンでデータサイエンティストとして働く大学院生です!
学部時代から長期インターンを始め、現在まで4社経験してきました。
この経験から、プログラミングの学習を始めたばかりの人や、長期インターンを行う勇気が出ない人に、学習サポートやデータ分析の実績作り支援、さらにはKaggle人材マッチングサービスなどを行わせてもらっています!
僕自身、プログラミングの習得や長期インターン探しに苦労したので、その経験をお伝えすることで、より多くの人が挫折せずデータサイエンティストになるまで成長して欲しいです!
以下でサポートを行なっているのでご興味ある方はご連絡ください!学生・社会人問わず専攻も問わずサポートいたします!
X(Twitter)
これまで機械学習アルゴリズムやデータサイエンティストに内定するまでに行ったこと、統計学実践ワークブックの解説などQiitaで記事にしているので、興味ある方はぜひ読んでみてください!
今回は、深層学習の登竜門、ニューラルネットワークに関して解説します👍
ニューラルネットワークとは
ニューラルネットワークは、脳の神経細胞ネットワークを模倣して設計された計算システムです。これは、機械学習の一分野であり、特にディープラーニングの核心技術として位置づけられています。複数の層から構成され、各層は多数のニューロン(またはノード)で構成されています。これらのニューロンは人間の脳のニューロンの働きを模倣したもので、入力信号を受け取り、加工して次のニューロンに送信します。
入力層はデータを受け取り、一連の隠れ層を経由して、最終的に出力層へと情報を渡します。隠れ層では、非線形変換が入力データに適用され、問題の複雑さに応じてネットワークを深くすることができます。ニューラルネットワークの訓練は、通常、大量のデータを使用して行われ、モデルは特定のタスク(例えば画像の分類、テキストの生成等)において高い性能を発揮するように調整されます。
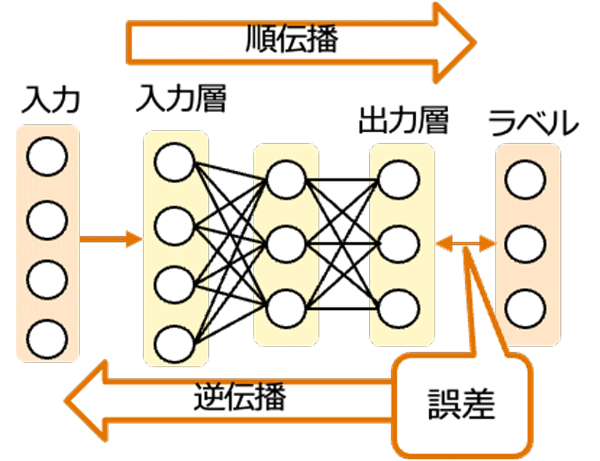
引用元:https://xtrend.nikkei.com/atcl/contents/technology/00007/00053/
順伝播アルゴリズム
順伝播は、入力データがネットワークの初めから終わりまで一方向に流れるプロセスです。データは入力層から始まり、隠れ層を通過し、最終的に出力層で予測や分類結果を生成します。各ニューロンでは以下の計算が行われます。
a^{(l)}_j = \sigma\left(\sum_{i} w^{(l)}_{ij} a^{(l-1)}_i + b^{(l)}_j\right)
ここで、$a_j^{(l)}$は層$l$のニューロン$j$の活性化出力、$σ$は活性化関数、$w_{ij}^{(l)}$は層$l$の重み、$b_j^{(l)}$はバイアス、$a_j^{(l-1)}$は前層$l-1$のニューロン$i$の出力です。
活性化関数
活性化関数はニューロンの出力を決定する重要な要素であり、非線形性をネットワークに導入する役割があります。以下にいくつかの一般的な活性化関数を紹介します。
1. シグモイド関数(Sigmoid Function)
\sigma(x) = \frac{1}{1 + e^{-x}}
シグモイド関数は、出力を0から1の間に制限します。これは、特に二値分類問題の出力層でよく使用されます。
2. ReLU(Rectified Linear Unit)
\text{ReLU}(x) = \max(0, x)
ReLUは、負の入力に対しては0を出力し、正の入力に対してはそのままの値を出力します。計算が効率的であり、多くの場合で優れた性能を発揮します。
3. tanh(ハイパボリックタンジェント関数)
\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}
tanh関数は出力を-1から1の間に制限します。これは、出力の平均を0に近づけることで学習の速度を向上させることができるため、隠れ層でよく使用されます。
これらの活性化関数は、ニューラルネットワークが複雑な非線形関係を学習するのを助けます。各関数は特定の用途に適しており、問題に応じて適切な関数を選択することが重要です。
順伝播プロセスでは、これらの活性化関数が各層のニューロンに適用され、最終的な出力に至るまでの各ステップで非線形変換を提供します。これにより、ネットワークは線形モデルでは捉えられない複雑なデータのパターンを学習する能力を得ます。
逆伝播アルゴリズム
逆伝播は、ネットワークを通じて誤差を後方に伝播させ、各重みの勾配を計算することでネットワークを学習させる方法です。このアルゴリズムは、出力層から入力層へと逆方向に作用し、勾配降下法(またはその変種)を使用して各重みを更新します。誤差は予測と実際のラベルとの差として計算され、この情報を使って重みを調整します。連鎖律を使用して各重みに対するコスト関数の勾配を計算することができます。
連鎖律
連鎖律は、合成関数の微分に関するルールです。合成関数とは、2つ以上の関数が組み合わさってできる関数のことを指します。例えば、ある関数が$f(g(x))$の形をしているとき、$f$と$g$は合成関数の関係にあります。
ニューラルネットワークでは、多くの合成関数が連なっており、一つの層の出力が次の層の入力になっています。このようなネットワーク全体を通じて、最終的なコスト(損失)関数までどのように各重みが影響しているかを知るために、連鎖律を用います。
連鎖律を使うと、ある関数の局所的な微分(勾配)を他の関数の局所的な微分と掛け合わせることで、複数の関数が組み合わさった全体の微分を計算できます。具体的には、次のような形式で表されます。
\frac{d}{dx} [f(g(x))] = f'(g(x)) \cdot g'(x)
この式は、$f(g(x))$の$x$に対する導関数は、$f$の$g(x)$に対する導関数と、$g$の$x$に対する導関数の積であることを示しています。
ニューラルネットワークの文脈では、コスト関数$C$の重み$w$に関する偏微分は、連鎖律を使って以下のように計算されます。
\frac{\partial C}{\partial w^{(l)}_{ij}} = \frac{\partial z^{(l)}_j}{\partial w^{(l)}_{ij}} \cdot \frac{\partial a^{(l)}_j}{\partial z^{(l)}_j} \cdot \frac{\partial C}{\partial a^{(l)}_j}
ここで、$a$は活性化関数の出力、$z$はその層の重み付き入力です。この式は、コスト関数の変化率(偏微分)が、活性化関数の出力に対するコストの変化率、活性化関数の勾配、および重みに対する重み付き入力の変化率の積であることを示しています。
この連鎖律によって、ネットワークのどの部分が最終的な誤差に最も影響を与えているかを特定でき、それに基づいて重みを効果的に調整することが可能になります。各層を逆方向に進みながら、重みを更新するための勾配を計算し、これによりネットワーク全体が期待する出力に近づくように学習が進んでいきます。
この連鎖律は、ニューラルネットワークが複雑な関数を学習できるようにするための基礎となるものであり、逆伝播アルゴリズムを理解する上で非常に重要です。連鎖律を通じて、ネットワークの各重みが最終的な出力にどのように影響を及ぼしているかを効率的に計算し、ネットワークの性能を最適化することができます。
実装例
データセットはscikit-learnからインポートし、モデルの実装はPyTorchを使用します。ここでは、MNISTデータセットを使用して、手書き数字の分類モデルを訓練します。
まず、scikit-learnからMNISTデータセットをロードします。
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
# MNIST データセットをロード
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
次に、PyTorchでネットワークを構築し、訓練します。
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import TensorDataset, DataLoader
import numpy as np
# データをPyTorchのテンソルに変換
X_train_tensor = torch.tensor(X_train.values.astype(np.float32))
y_train_tensor = torch.tensor(y_train.values.astype(np.int64))
train_dataset = TensorDataset(X_train_tensor, y_train_tensor)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
class SimpleNN(nn.Module):
def __init__(self):
super(SimpleNN, self).__init__()
self.fc1 = nn.Linear(784, 128)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.relu(self.fc1(x))
x = self.fc2(x)
return x
model = SimpleNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 訓練ループ
for epoch in range(10): # エポック数
for data, target in train_loader:
optimizer.zero_grad()
output = model(data)
loss = criterion(output, target)
loss.backward()
optimizer.step()
訓練プロセス
モデルを訓練するには、エポック数とバッチサイズを定義する必要があります。エポック数は、訓練データセットを何回繰り返して学習させるかを示し、バッチサイズは、一度にネットワークに供給するサンプルの数です。
-
エポック数(Epochs)
モデルが訓練データセット全体を通過する回数。多くのエポックを実行すると、モデルは訓練データからより多くを学ぶことができますが、過学習(トレーニングデータに過剰に適合すること)のリスクも高まります。 -
バッチサイズ(Batch size)
一度にネットワークに供給されるデータの数。バッチサイズが大きいと、各エポックの計算速度は速くなりますが、メモリ使用量も増加し、訓練の精度が低下する可能性があります。
このコードでは、PyTorchのデータローダーを使用して訓練データをモデルに供給し、損失関数と最適化アルゴリズムを使用してモデルを訓練しています。各エポックで全ての訓練データがモデルによって一度処理され、バッチサイズに基づいてデータが小分けにされてネットワークに供給されます。
さいごに
最後まで読んでいただきありがとうございました!
少しでもデータサイエンスを学ぶ方の一助となればと思います。
いいなと思った方は「いいね」お願いいたします。
もし僕の活動にもご興味を持っていただけたら、X(Twitter)もフォローしていただけると嬉しいです!
X(Twitter)