はじめに
こんにちは!
僕は研究を行いながら、長期インターンでデータサイエンティストとして働く大学院生です!
学部時代から長期インターンを始め、現在4社経験してきました。
この経験から、プログラミングの学習を始めたばかりの人や、長期インターンを行う勇気が出ない人に、学習サポートやデータ分析の実績作り支援などを行わせてもらっています!
僕自身、プログラミングの習得や長期インターン探しに苦労したので、その経験をお伝えすることで、より多くの人が挫折せずデータサイエンティストになるまで成長して欲しいです!
以下でサポートを行なっているのでご興味ある方はご連絡ください!学生・社会人問わず専攻も問わずサポートいたします!
X(Twitter)
今回は、実務や研究でもよく利用される決定木手法について解説します👍
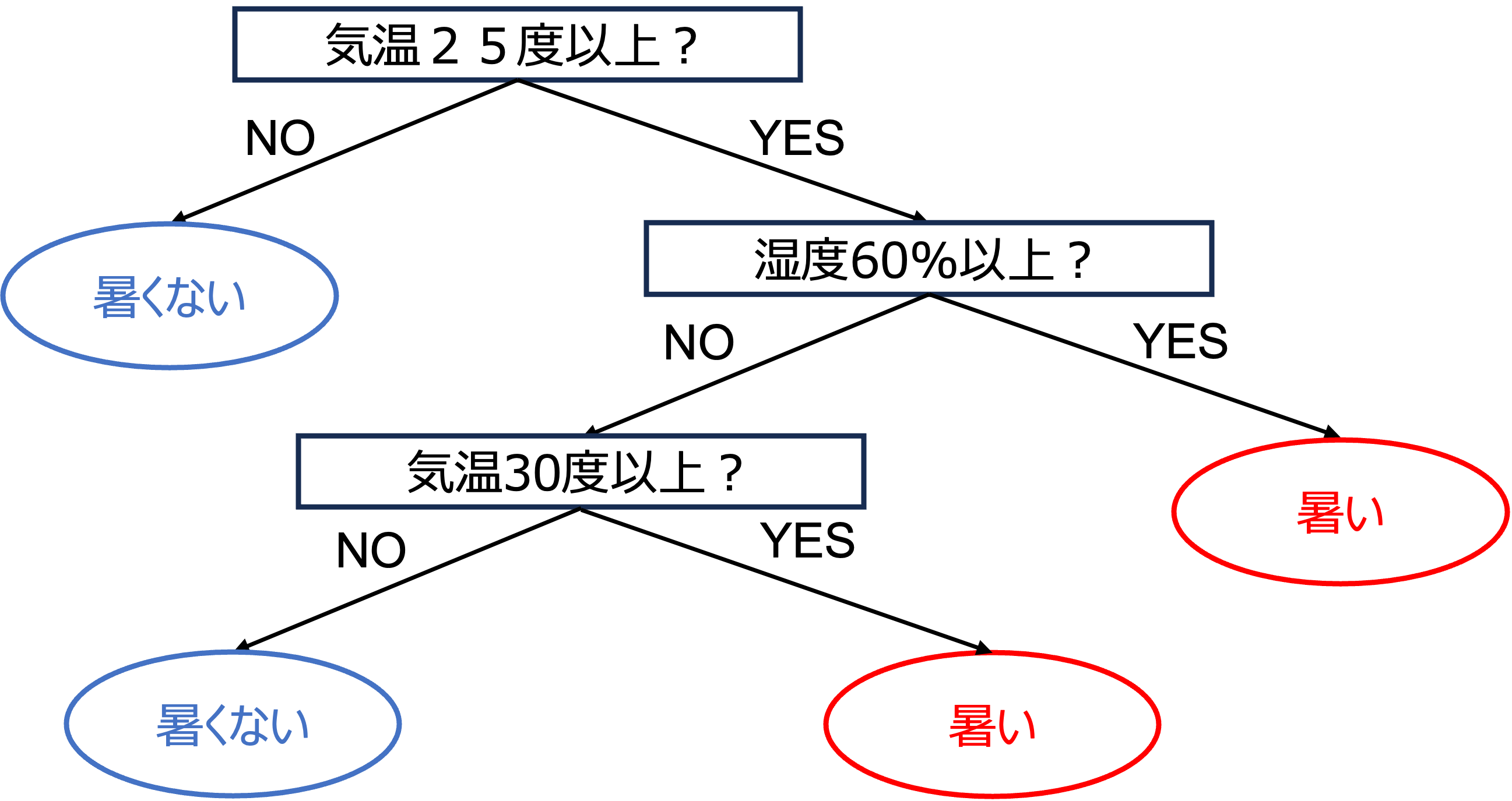
決定木とは
決定木は、データを分類するための機械学習アルゴリズムであり、同時に回帰タスクにも用いられる柔軟なツールです。このアルゴリズムは、分岐する木構造を通じて、データセットをより単純なサブセットに分割し、最終的に分類または連続値の予測を行います。
使用される具体的な場面
決定木は、その直感的な理解と可視化の容易さから、さまざまな場面で広く使用されています。例えば、医療分野では病気の診断、金融ではクレジットスコアリング、マーケティングでは顧客セグメンテーション、製造業では品質管理などに利用されます。特に、データの特徴や関係性を明確に示す必要がある場合、決定木は非常に有効です。
学習アルゴリズム
決定木のアルゴリズムは、トレーニングデータを分割して分析する方法で、データセットをより単純なサブセットに分解することで、最終的にはデータを分類または回帰するために使用されます。このプロセスは、ジニ不純度または情報利得といった特定の指標に基づいて行われます。
ジニ不純度(Gini Impurity)
ジニ不純度は、ランダムに選んだ要素が誤って分類される確率を測定します。これは、ノード(決定木の各分岐点)の「純度」を評価するために使用され、値が低いほど、そのノードは純粋になります(つまり、同じクラスの要素が多く含まれます)。ジニ不純度は以下の式で計算されます:
I_G(p)=1-\sum_{j=1}^{J}p_j^2
ここで$p_j$はクラス$j$に属する要素の割合です。
たとえば、あるノードに2つのクラスが等しく分割されている場合、ジニ不純度は $1-(0.5^2+0.5^2)=0.5$となります。これはそのノードが完全に不純であることを意味します。
情報利得(Information Gain)
情報利得は、分割によってどれだけ情報が得られたかを測定します。具体的には、分割前のノードの不純度から、分割後のすべての子ノードの不純度を差し引いた値です。情報利得が大きいほど、その分割はデータセットをより良く分割しています。情報利得は以下の式で計算されます:
IG(D_p,f)=I(D_p)-\sum_{j=1}^m\frac{N_j}{N_p}I(D_j)
ここで、$IG$は情報利得、$D_p$は親ノードのデータセット、$D_j$は$j$番目の子ノードのデータセット、$N_p$は親ノードのデータ点数、$N_j$は子ノードのデータ点数、$I$は不純度指標(例えばジニ不純度)です。
決定木の構築
決定木の構築は、以下のステップに従って行われます:
- 最適な分割を見つける: データセットを分割する最良の方法を選ぶために、すべての特徴量とその可能な分割点について、情報利得またはジニ不純度を計算します。
- ノードの分割: 最も情報利得が高い、またはジニ不純度が最も低い特徴量とその閾値を選択してノードを分割します。
- 終了条件のチェック: 木の深さの制限、ノード内の最小データ数、情報利得の最小改善など、事前に設定された終了条件を確認します。
- 再帰的分割: 上記のプロセスを各子ノードに対して再帰的に繰り返し、終了条件に達するまで続けます。
決定木は、その直観的な理解や可視化の容易さから、分類とデータ探索の両方に有用です。しかし、過学習の傾向があるため、モデルの複雑さに注意深くアプローチする必要があります。
注意点
特徴量の重要度
決定木では、各特徴量が分類や回帰タスクにおいてどれだけ重要かを算出できます。これは特徴量の重要度として知られており、特徴量が分割に使用される頻度とその分割で得られる情報利得の平均を基に計算されます。算出方法は以下の通りです:
- 特徴量ごとの情報利得の算出:各特徴量が使われる際の情報利得を計算します。
- 特徴量の重要度の算出:すべてのノードでその特徴量を使って得られた情報利得の平均を求め、それを正規化して各特徴量の重要度とします。
これにより、モデルがどの特徴量を重視しているかを理解し、特徴量の選択やモデルの改善に役立てることができます。
過学習
決定木は過学習(オーバーフィッティング)する傾向があります。これを防ぐための方法はいくつかあります:
- 木の深さの制限: 決定木の深さを制限することで、モデルが訓練データに過剰に適合するのを防ぎます。
- 枝刈り(Pruning): 木が完全に成長した後、情報利得が最小限の閾値未満のノードを削除します。
- ランダムフォレスト: 複数の決定木を組み合わせることで、個々の決定木の過学習を相殺します。
- クロスバリデーション: データセットを複数のサブセットに分割し、それぞれでモデルのトレーニングと検証を行います。これにより、モデルの一般化能力を評価できます。
- グリッドサーチ(Grid Search): ハイパーパラメータ(例:木の深さ、枝刈りの閾値など)の最適な組み合わせを見つけるために、様々な値の組み合わせでモデルをトレーニングし、最良の組み合わせを選択します。
これらの手法を適用することで、決定木の過学習を効果的に減少させ、より一般化された予測モデルを構築することができます。
実装例
Pythonを用いて決定木の例を示します。ここでは、scikit-learnライブラリを使用して、決定木のモデルをトレーニングし、特徴量の重要度を算出・可視化し、モデルの精度も評価します。
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
# データセットのロード
iris = load_iris()
X = iris.data
y = iris.target
# トレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 決定木のトレーニング
tree = DecisionTreeClassifier(max_depth=3, random_state=42)
tree.fit(X_train, y_train)
# テストデータでのモデル評価
y_pred = tree.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"モデルの精度: {accuracy:.2f}")
# 特徴量の重要度
feature_importance = tree.feature_importances_
# 決定木の可視化
plt.figure(figsize=(12, 8))
plot_tree(tree, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()
このコードでは、まずアイリスデータセットをロードして、トレーニングセットとテストセットに分割します。次に、決定木モデルをトレーニングセットでトレーニングし、テストセットで精度を評価します。また、特徴量の重要度を算出し、決定木を可視化しています。このプロセスは、決定木の基本的な使い方と、モデルの評価方法を理解するのに役立ちます。
さいごに
最後まで読んでいただきありがとうございました!
少しでもデータサイエンティストを目指す方の一助となればと思います。
もし僕の活動にもご興味を持っていただけたら、X(Twitter)もフォローしていただけると嬉しいです!
X(Twitter)
参考文献
- 「決定木アルゴリズム徹底解説:基本概念、歴史、メリット・デメリット、実用例、プログラミング言語での実装方法」
https://reinforz.co.jp/bizmedia/5369/
+「[入門]初心者の初心者による初心者のための決定木分析」
https://qiita.com/3000manJPY/items/ef7495960f472ec14377 - 「決定木について分かりやすく解説!PythonとRで実装してみよう!」
https://toukei-lab.com/%E6%B1%BA%E5%AE%9A%E6%9C%A8