機械学習とは何か(ついでにsin(θ)を人工知能で計算)
「機械学習」についての私の理解を示します。ついでにsin(θ)を「人工知能」を使って計算してみたいと思います。
機械学習とは何か
私の理解
機械学習は、人工知能を実現する手段の一つです。
従来の人工知能(=シンボリックAI)は、説明可能性を重視し、演繹的(論理学的)アプローチを取っていました。しかし、そのアプローチは、限界にぶつかっていました。シンボリックAIでは、コンピュータにアルゴリズムやルールを教える必要がありますが、対象分野によっては、アルゴリズムやルールを見つけることが難しいためです。
それに対し、機械学習は、説明可能性を一定程度あきらめ、帰納的(統計学的)アプローチを取り入れました。すなわち、コンピュータにデータ(=サンプルデータ)を与え、データの統計学的処理(=訓練)を重ねさせ、経験的に妥当なモデルを作らせることにしたのです。
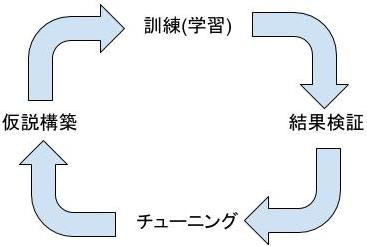
人間は、データを用意し、学習効果を測定する基準を考え、モデルの枠組み(=仮説)を構築します。仮説が構築できたら、コンピュータに訓練を実行させ、モデルを完成させます。訓練が終わったら、基準に照らし、学習効果(=モデルがどれだけ表現力を身に付けたか)を測定します。測定結果を検証し、パラメータのチューニングを行います。モデルが十分な表現力を得るまで、リソースと相談しつつ、一連のサイクルを繰り返します。
モデルが十分な表現力を得たと判断できたら、アプリケーションに組み込み、現実世界の問題を解くのに利用します。
なお、機械学習には、線形回帰、ロジスティック回帰、サポートベクターマシン、ランダムフォレスト等の技術があります。それらのクラシカルな機械学習と比べ、より説明可能性をあきらめた(=帰納的アプローチの度合いを高めた)のが、ディープラーニングです。ディープラーニングは、機械学習の対象分野を広げることに成功しました。
機械学習は、帰納的アプローチをとる関係上、多くのリソースを必要とします。訓練では、データ量と訓練回数、モデルの複雑さに応じ、消費するリソースが増大します。仮説の検証を何度も繰り返せば、さらにリソースが増大します。すなわち、多くのマシンパワー(空間)を使うか、多くの時間を使うかとなります。
ディープラーニングでは、特に多くのリソースを消費します。クラシカルな機械学習で済むなら済ませるべきだし、そもそも、本当にアルゴリズムやルールを見つけることができないか、一度は考えてみるべきです。
反省
以上のように理解しましたが、以下の点を反省します。
- 統計学は、むしろ説明のための学問である。説明可能性をあきらめて統計学的アプローチを取り入れた、という表現には違和感を感じる。単に、統計学で利用している数学とアルゴリズムを、取り入れただけではないか。
- 果たして、ディープラーニングは説明可能性をあきらめてしまったのか。それは2018年夏現在の状況を示しているだけで、近い将来、説明可能性を獲得するのではないか。
参考文献、参考サイト
- François Chollet著(2017)、クイーブ訳(2018)『PythonとKerasによるディープラーニング』マイナビ出版
- Drew Conway(2010)『The Data Science Venn Diagram』
- 丸山宏『演繹から機能へ 〜新しいシステム開発パラダイム〜』
- 丸山宏「機械学習工学に向けて」『機械学習型システム開発へのパラダイム転換』国立研究開発法人科学技術振興機構 研究開発戦略センター
-
Tom Mitchell(1998)による定義
- コンピュータプログラムが、ある種のタスクTと評価尺度Pにおいて、経験Eから学習するとは、タスクTにおけるその性能をPによって評価した際に、経験Eによってそれが改善されている場合である
- 佐伯竜輔(2018)『AIブームを支える「機械学習」~AIの現実的な始め方とは?』DB Press
-
Arthur Samuel(1959)による定義
- 機械学習とは「明示的にプログラムしなくても学習する能力をコンピュータに与える研究分野」である
- Wikipedia『Symbolic artificial intelligence』
sin(θ)を人工知能に計算させる
さて、それでは、以下四つのアプローチで、sin(θ)を計算させてみたいと思います。
- 幾何学的計算
- 解析学的計算
- クラシカルな機械学習による計算
- ディープラーニングによる計算
動作確認は、以下環境で行なっています。
- Python 3.6.4
- tensorflow 1.9.0
- Keras 2.2.0
また、以下の記事に従い、毎回%matplotlib inlineと書かなくて良いように設定済みであるとします。
幾何学的計算
従来の人工知能(=シンボリックAI)のアプローチで、sin(θ)を計算させてみましょう。そのためにはコンピュータにアルゴリズムを教える必要があります。アルゴリズムは、プログラミングすることにより、教えることができます。
sin(θ)は、幾何学的には「x軸との角度がθとなるような直線と単位円の交点のy座標」として定義されます。コンピュータにsin(θ)を計算させるためには、どうプログラミングすればよいでしょう。
ゆるゆるプログラミングというサイトでは、x軸とy軸に単位ベクトルを配置し、目的の角度に十分近づくまで、両側から「挟み撃ち」していくようなアルゴリズムが紹介されています。アルゴリズムの詳しい説明はサイトをご参照ください。サイトに記載のJavaプログラムをPythonに移植の上、手を加えたものを、以下に記載します。
from math import pi, radians, sqrt
from numpy import absolute, frompyfunc, sin
import matplotlib.pyplot as plt
from statistics import mean, stdev
def _sin1(θ):
# 角度θを0.0~359.999...の範囲に直す
while True:
if θ < 0.0:
θ += 2.0 * pi
continue
if 2.0 * pi <= θ:
θ -= 2.0 * pi
continue
break
# 180度を超える場合、x軸に関して対称とする
if pi < θ:
return -1 * _sin1(2.0 * pi - θ)
# 90〜180度の場合、y軸に関して対称とする
if 0.5 * pi < θ:
return _sin1(pi - θ)
# 結果の初期化
ans_sin = 0.0
# 角度に応じて分岐する
if θ == 0:
ans_sin = 0.0
elif θ == 0.5 * pi:
ans_sin = 1.0
else:
θ1, θ2 = 0.0, 0.5 * pi
x1, y1 = 1.0, 0.0
x2, y2 = 0.0, 1.0
delta = 0.0000000000000001
loopnumber = 0
# l = []
# s = []
# 無限ループ
while True:
# ループ回数
loopnumber += 1
# l.append(loopnumber)
# 角度、座標の中間値を計算
θm, xm, ym = (θ1 + θ2) / 2.0, (x1 + x2) / 2.0, (y1 + y2) / 2.0
# 原点(0,0)と(xm,ym)を結ぶ線の単位ベクトル(new_x, new_y)を計算
d = sqrt(xm ** 2 + ym ** 2)
new_x, new_y = xm / d, ym / d
# s.append(new_y)
# 角度の差がdelta未満で終了
if absolute(θm - θ) < delta:
ans_sin = new_y
'''
# 収束状況を表示
print("ループ回数:" + str(loopnumber))
plt.plot(l, s, marker='.')
plt.grid()
plt.xlabel('ループ回数')
plt.ylabel('sin(θ)')
plt.show()
'''
break
# 角度を狭める
if (θ > θm):
x1, y1, θ1 = new_x, new_y, θm
else:
x2, y2, θ2 = new_x, new_y, θm
return ans_sin
def sin1(θ):
return frompyfunc(_sin1, 1, 1)(θ)
deg = 30.0
rad = radians(deg)
x = sin1(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
deg = 45.0
rad = radians(deg)
x = sin1(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
deg = 60.0
rad = radians(deg)
x = sin1(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
rads = [radians(i) for i in range(0, 359)]
h = sin1(rads)
y = sin(rads)
e = absolute(y - h)
print("誤差最大値 :" + str(max(e)))
print("誤差最小値 :" + str(min(e)))
print("誤差平均値 :" + str(mean(e)))
print("誤差標準偏差:" + str(stdev(e)))
独自関数によるsin(30.0):0.5000000000000004
組込関数によるsin(30.0):0.49999999999999994
独自関数によるsin(45.0):0.7071067811865475
組込関数によるsin(45.0):0.7071067811865475
独自関数によるsin(60.0):0.8660254037844387
組込関数によるsin(60.0):0.8660254037844386
誤差最大値 :5.551115123125783e-16
誤差最小値 :0.0
誤差平均値 :1.386164670430837e-16
誤差標準偏差:1.1688186600394947e-16
高精度な値が得られています。コンピュータが、sin(θ)に関して知能を獲得したと言えます。また、プログラムの内容が説明可能であるところに、好感がもてます。説明可能なツールは、安心して利用できるためです。
解析学的計算
さて、数学の世界には、テイラー展開と呼ばれる技法があります。テイラー展開を用いることにより、以下の等式が得られます。
$$
sin(\theta) = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + \frac{\theta^9}{9!} + ...
$$
オイラーの等式:$e^{i\pi} + 1 = 0$にもつながる、美しい等式です。この等式の右辺を用いてコンピュータにsin(θ)を計算させることもできるわけですが、そもそも、この右辺はいったい何をしているのでしょうか。
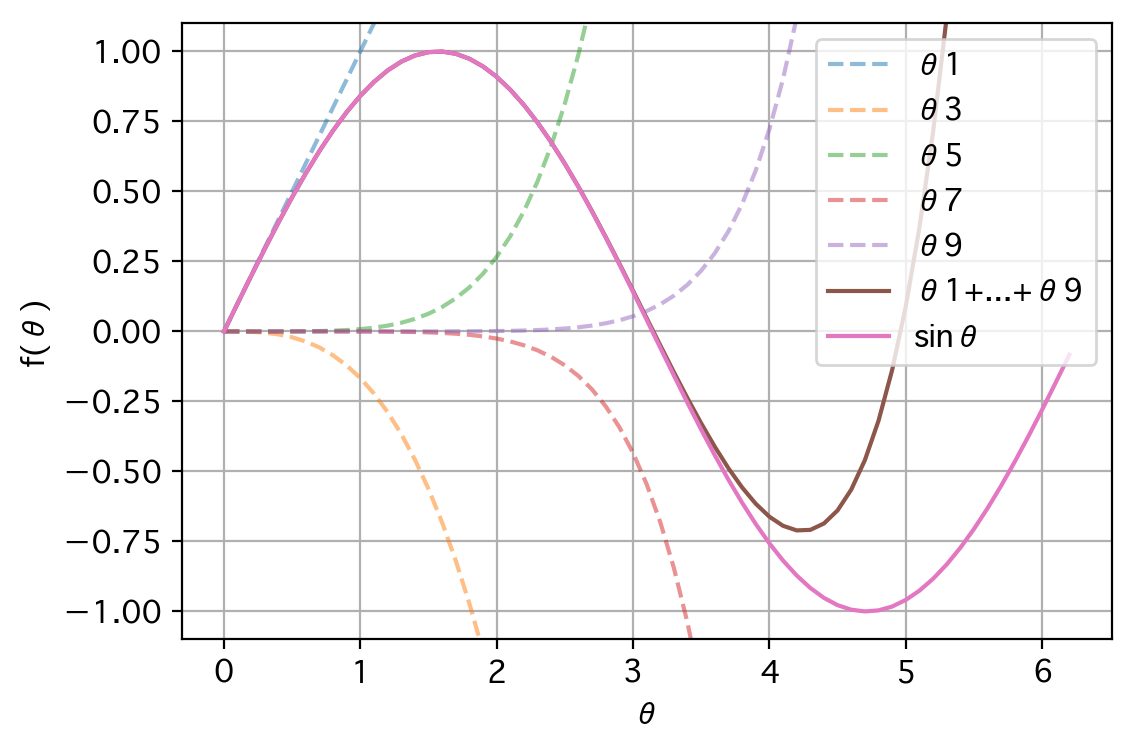
実は、この右辺は、いくつもの曲線を合成することで、サインカーブを再現しようとしています。
from math import factorial, pi
from numpy import arange, sin
import matplotlib.pyplot as plt
θ = arange(0, 2.0 * pi, 0.1)
θ1 = θ
θ3 = -θ**3 / factorial(3)
θ5 = θ**5 / factorial(5)
θ7 = -θ**7 / factorial(7)
θ9 = θ**9 / factorial(9)
θall = θ1 + θ3 + θ5 + θ7 + θ9
sinθ = sin(θ)
plt.figure()
plt.plot(θ, θ1, label='θ1', linestyle='--', alpha=0.5)
plt.plot(θ, θ3, label='θ3', linestyle='--', alpha=0.5)
plt.plot(θ, θ5, label='θ5', linestyle='--', alpha=0.5)
plt.plot(θ, θ7, label='θ7', linestyle='--', alpha=0.5)
plt.plot(θ, θ9, label='θ9', linestyle='--', alpha=0.5)
plt.plot(θ, θall, label='θ1+...+θ9')
plt.plot(θ, sinθ, label='sinθ')
plt.legend()
plt.ylim([-1.1, 1.1])
plt.grid()
plt.xlabel('θ')
plt.ylabel('f(θ)')
plt.show()
たった5つの曲線の合成でも、θ=3.5あたりまでは、それらしく再現できていることがわかります。
では、これをふまえて、解析学的にsin(θ)を計算するアルゴリズムを、コンピュータに教えることにしましょう。
from math import factorial, pi, radians
from numpy import absolute, frompyfunc, sin
from statistics import mean, stdev
def _sin2(θ):
# 角度θを0.0~359.999...の範囲に直す
while True:
if θ < 0.0:
θ += 2.0 * pi
continue
if 2.0 * pi <= θ:
θ -= 2.0 * pi
continue
break
# 180度を超える場合、x軸に関して対称とする
if pi < θ:
return -1 * _sin2(2.0 * pi - θ)
# 90〜180度の場合、y軸に関して対称とする
if 0.5 * pi < θ:
return _sin2(pi - θ)
return sum([(-1)**(i-1) * θ**(2*i-1) / factorial(2*i-1) for i in range(1, 12)])
def sin2(θ):
return frompyfunc(_sin2, 1, 1)(θ)
deg = 30.0
rad = radians(deg)
x = sin2(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
deg = 45.0
rad = radians(deg)
x = sin2(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
deg = 60.0
rad = radians(deg)
x = sin2(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
rads = [radians(i) for i in range(359)]
h = sin2(rads)
y = sin(rads)
e = absolute(y - h)
print("誤差最大値 :" + str(max(e)))
print("誤差最小値 :" + str(min(e)))
print("誤差平均値 :" + str(mean(e)))
print("誤差標準偏差:" + str(stdev(e)))
独自関数によるsin(30.0):0.49999999999999994
組込関数によるsin(30.0):0.49999999999999994
独自関数によるsin(45.0):0.7071067811865475
組込関数によるsin(45.0):0.7071067811865475
独自関数によるsin(60.0):0.8660254037844385
組込関数によるsin(60.0):0.8660254037844386
誤差最大値 :3.3306690738754696e-16
誤差最小値 :0.0
誤差平均値 :1.1695900013687744e-16
誤差標準偏差:9.066751491381523e-17
またしても、高精度な値が得られています。コンピュータが、sin(θ)に関してさらなる知能を獲得したと言えます。しかし、テイラー展開を知らない人間に対しては、説明のしようのないプログラムではあります。でも、それは仕方ないでしょう。以下等式が成り立つことは数学的事実なのです。それゆえ、ツールの妥当性は担保されており、安心して利用できると言えます。
$$
sin(\theta) = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + \frac{\theta^9}{9!} + ...
$$
さて、sin(θ)の計算方法を二つ、コンピュータに教えたわけですが、両者の性能を比較してみましょう。
from math import radians
deg = 30.0
rad = radians(deg)
%timeit x = sin1(rad)
%timeit x = sin2(rad)
64.1 µs ± 502 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
9.16 µs ± 62.9 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
解析学的な計算方法の方が約7倍速いという結果となりました。数学者ブルック・テイラーは偉大ですね。
クラシカルな機械学習による計算
クラシカルな機械学習による手法(重回帰分析)で、コンピュータにsin(θ)を計算させてみましょう。まず「sin(θ)がθのn次の多項式で表現できる」という仮説を立てます。
$$sin(\theta) = b_1\theta^1 + b_2\theta^2 + b_3\theta^3 ...$$
次に、0から0.5πの間に無数に存在する実数の内、300個をサンプルデータとして与えます。そして、統計学的処理(=訓練)を実行させ、回帰係数(=重み)bを推定させます。最後に、そうしてできたモデルをつかって、sin(θ)を計算するという流れです。
from os import mkdir
from os.path import exists
from sys import exc_info
from math import pi, radians
from numpy import absolute, array, arange, frompyfunc, sin
from pandas import DataFrame
from sklearn.externals.joblib import dump, load
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from statistics import mean, stdev
class MregSin:
# モデル
modeldir = './data'
modelfile = './data/MregSin.pkl'
# データに関するパラメータ
number_of_train_data = 300
start_of_train_data = 0.0 * pi
stop_of_train_data = 0.5 * pi
# モデルに関するパラメータ
number_of_features = 11
# 訓練に関するパラメータ
# 特になし
def __init__(self, recycle=True):
if recycle and exists(MregSin.modelfile):
try:
print('訓練済みモデルを読み込みます。')
self.__model = load(MregSin.modelfile)
except:
print('訓練済みモデルの読み込み中にエラーが発生しました。')
print('Unexpected error:', exc_info()[0])
raise
else:
print('訓練を行うので、お待ちください。')
# データ
feature_names = [str(i) for i in
range(1, MregSin.number_of_features + 1, 1)]
x = arange(MregSin.start_of_train_data, MregSin.stop_of_train_data,
(MregSin.stop_of_train_data - MregSin.start_of_train_data)
/ MregSin.number_of_train_data)
data = [[i**j for j in
range(1, MregSin.number_of_features + 1, 1)] for i in x]
target = sin(x)
# モデル
self.__model = LinearRegression()
# 訓練
self.__model.fit(data, target)
# 訓練状況の可視化
print('回帰係数')
coefficient = DataFrame({'feature' : feature_names
, 'coefficient' : self.__model.coef_})
print(coefficient)
print('切片')
print(self.__model.intercept_)
# 予測
x2 = [x[i] for i in
range(0, len(x), round(0.02 * MregSin.number_of_train_data))]
data2 = [[i**j for j in
range(1, MregSin.number_of_features + 1, 1)] for i in x2]
target2 = [target[i] for i in
range(0, len(target), round(0.02 * MregSin.number_of_train_data))]
predicted = self.__model.predict(data2)
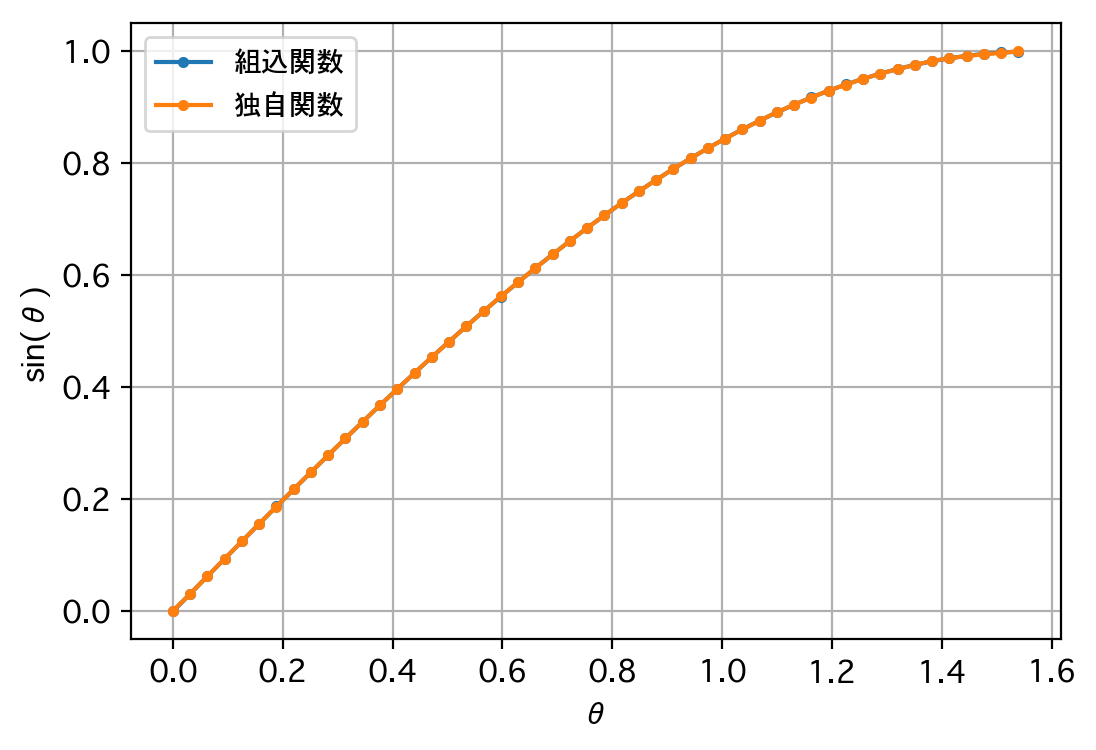
plt.figure()
plt.plot(x2, target2, marker='.', label='組込関数')
plt.plot(x2, predicted, marker='.', label='独自関数')
plt.legend(loc='best', fontsize=10)
plt.grid()
plt.xlabel('θ')
plt.ylabel('sin(θ)')
plt.show()
# モデルの保存
if not exists(MregSin.modeldir):
try:
mkdir(MregSin.modeldir)
except:
print('モデル保存フォルダの作成中にエラーが発生しました。')
print('Unexpected error:', exc_info()[0])
raise
try:
dump(self.__model, MregSin.modelfile)
except:
print('モデルの保存中にエラーが発生しました。')
print('Unexpected error:', exc_info()[0])
raise
def __sin(self, θ):
# 角度θを0.0~359.999...の範囲に直す
while True:
if θ < 0.0:
θ += 2.0 * pi
continue
if 2.0 * pi <= θ:
θ -= 2.0 * pi
continue
break
# 180度を超える場合、x軸に関して対称とする
if pi < θ:
return -1 * self.sin(2.0 * pi - θ)
# 90〜180度の場合、y軸に関して対称とする
if 0.5 * pi < θ:
return self.sin(pi - θ)
data = [[θ**i for i in range(1, MregSin.number_of_features + 1, 1)]]
return self.__model.predict(data)[0]
def sin(self, θ):
return frompyfunc(self.__sin, 1, 1)(θ)
ds = MregSin(recycle=False)
deg = 30.0
rad = radians(deg)
x = ds.sin(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
deg = 45.0
rad = radians(deg)
x = ds.sin(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
ds = MregSin()
deg = 60.0
rad = radians(deg)
x = ds.sin(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
rads = [radians(i) for i in range(359)]
h = ds.sin(rads)
y = sin(rads)
e = absolute(y - h)
print("誤差最大値 :" + str(max(e)))
print("誤差最小値 :" + str(min(e)))
print("誤差平均値 :" + str(mean(e)))
print("誤差標準偏差:" + str(stdev(e)))
訓練を行うので、お待ちください。
回帰係数
feature coefficient
0 1 1.000000e+00
1 2 -2.602449e-10
2 3 -1.666667e-01
3 4 -1.611588e-08
4 5 8.333389e-03
5 6 -1.227027e-07
6 7 -1.982343e-04
7 8 -1.720502e-07
8 9 2.863353e-06
9 10 -4.069894e-08
10 11 -1.754363e-08
切片
-8.915090887740007e-14
独自関数によるsin(30.0):0.5000000000000134
組込関数によるsin(30.0):0.49999999999999994
独自関数によるsin(45.0):0.7071067811865207
組込関数によるsin(45.0):0.7071067811865475
訓練済みモデルを読み込みます。
独自関数によるsin(60.0):0.8660254037844507
組込関数によるsin(60.0):0.8660254037844386
誤差最大値 :1.6620038678638593e-13
誤差最小値 :2.55351295663786e-15
誤差平均値 :2.1351626923889052e-14
誤差標準偏差:1.5984259514679425e-14
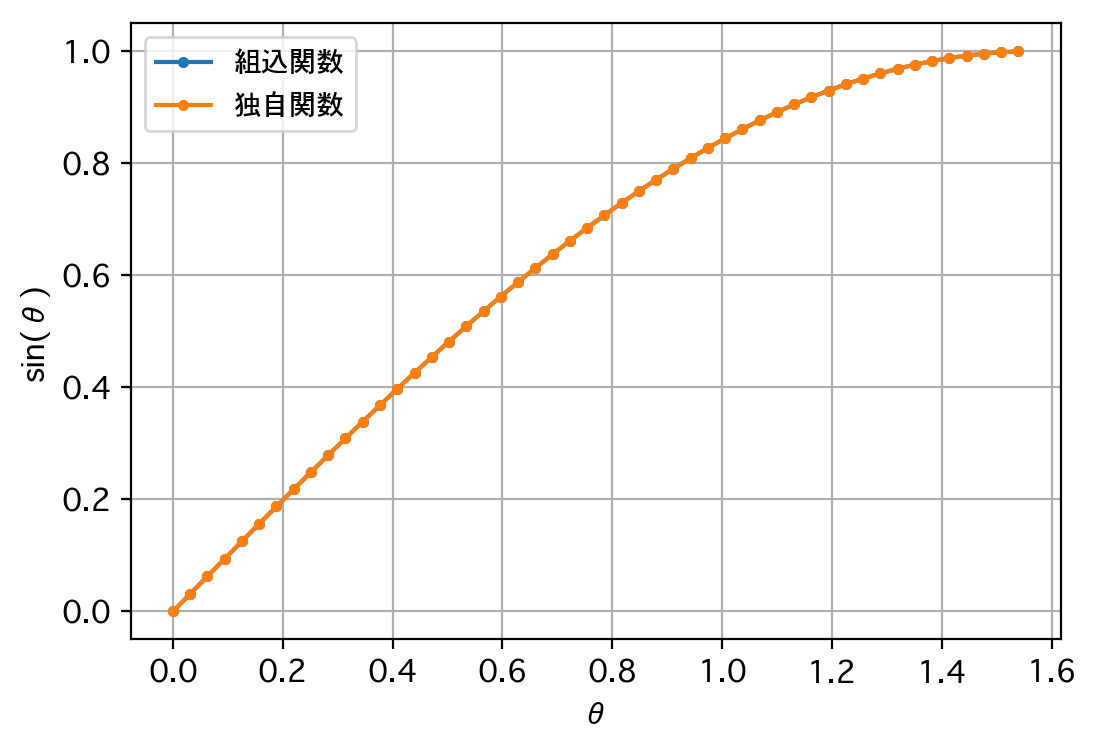
かなり、うまくいきましたね。もちろん、仮説が的確すぎた(=特徴量として最適なものを選んだ)ので、このような結果になるのも当然ですが…いずれにせよ、コンピュータがもう一つ、sin(θ)に関して、知能を獲得したと言えます。
しかし、なぜこの特徴量で良いのか、なぜこの重みで良いのか、説明できるでしょうか。「『sin(θ)がθのn次の多項式で表現できる』という仮説を立て、実際のデータを元に妥当な重みを計算。完成したモデルを検証用のデータで検証してみたところ、仮説が99.9%正しいことを証明できた。」といった説明しかできない気がします。統計学的に理論武装しておかないと、このツールの妥当性を説明できないかもしれませんね。
なお、このプログラムは、私が書いた初めてのscikit-learnプログラムとなります。公式サイトのほかに、以下サイトを参考にさせて頂きました。
- 誰でも出来る!!scikit-learn(sklearn)で重回帰分析しちゃう
- pandasの使い方(2) DataFrameの生成
- [Python3] scikit-learnによる機械学習4: 学習が完了したモデルを永続化する
ディープラーニングによる計算
最後に、ディープラーニングによって、コンピュータにsin(θ)を計算させてみましょう。0から0.5πの間に無数に存在する実数の内、30万個をサンプルデータとして与え、統計学的処理(=訓練)を実行させます。そうしてできたモデルをつかって、sin(θ)を計算するという流れです。
from os import mkdir
from os.path import exists
from sys import exc_info
from math import pi, radians
from numpy import absolute, arange, array, frompyfunc, sin
from keras.models import load_model, Sequential
from keras.layers import Dense, Dropout
from keras.callbacks import EarlyStopping
import matplotlib.pyplot as plt
from statistics import mean, stdev
class DeepSin:
# モデル
modeldir = './data'
modelfile = './data/DeepSin.h5'
# データに関するパラメータ
number_of_train_data = 300000
start_of_train_data = 0.0 * pi
stop_of_train_data = 0.5 * pi
number_of_test_data = 0.3 * number_of_train_data
start_of_test_data = 0.0
stop_of_test_data = 0.5 * pi
# モデルに関するパラメータ
number_of_layer = 10
units = 30
# 訓練に関するパラメータ
# min_delta = 0
# patience = 0
batch_size = round(0.01 * number_of_train_data)
epochs = 20
def __init__(self, recycle=True):
if recycle and exists(DeepSin.modelfile):
try:
print('訓練済みモデルを読み込みます。')
self.__model = load_model(DeepSin.modelfile)
except:
print('訓練済みモデルの読み込み中にエラーが発生しました。')
print('Unexpected error:', exc_info()[0])
raise
else:
print('訓練を行うので、お待ちください。')
# print('学習が頭打ちになった場合、途中で訓練を打ち切ります。')
# データ
trX = arange(DeepSin.start_of_train_data, DeepSin.stop_of_train_data,
(DeepSin.stop_of_train_data - DeepSin.start_of_train_data)
/ DeepSin.number_of_train_data)
trY = sin(trX)
valX = arange(DeepSin.start_of_test_data, DeepSin.stop_of_test_data,
(DeepSin.stop_of_test_data - DeepSin.start_of_test_data)
/ DeepSin.number_of_test_data)
valY = sin(valX)
# モデル
self.__model = Sequential()
self.__model.add(Dense(1, input_dim=1, activation='linear'))
for i in (range(DeepSin.number_of_layer)):
self.__model.add(Dense(DeepSin.units, activation='relu'))
self.__model.add(Dense(1))
self.__model.compile(loss='mean_squared_error', optimizer='Adam')
# 訓練
# early_stopping = EarlyStopping(monitor='val_loss'
# , min_delta=DeepSin.min_delta
# , patience=DeepSin.patience
# , mode='auto'
# )
hist = self.__model.fit(trX, trY,
batch_size=DeepSin.batch_size
, epochs=DeepSin.epochs
# , callbacks=[early_stopping]
, validation_data=(valX, valY)
)
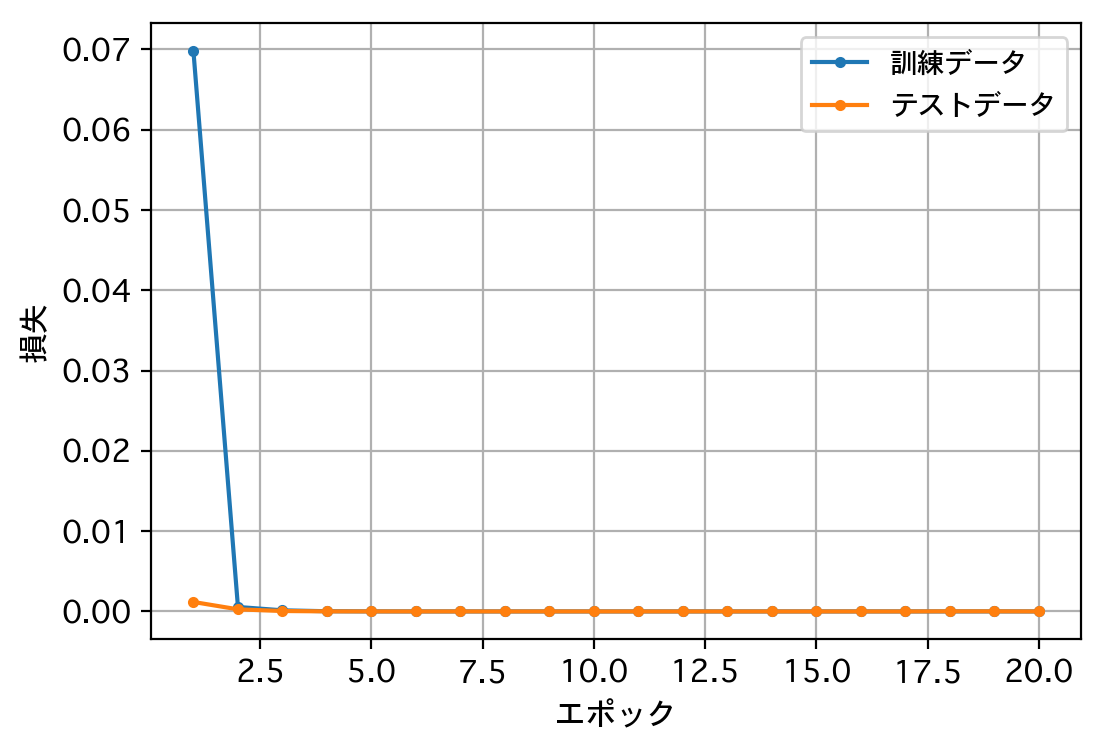
# 訓練状況の可視化
loss = hist.history['loss']
val_loss = hist.history['val_loss']
plt.figure()
plt.plot(range(1, len(loss) + 1),
loss, marker='.', label='訓練データ')
plt.plot(range(1, len(val_loss) + 1),
val_loss, marker='.', label='テストデータ')
plt.legend(loc='best', fontsize=10)
plt.grid()
plt.xlabel('エポック')
plt.ylabel('損失')
plt.show()
# 予測
trX2 = array([trX[i] for i in
range(0, len(trX), round(0.02 * DeepSin.number_of_train_data))])
trY2 = array([trY[i] for i in
range(0, len(trY), round(0.02 * DeepSin.number_of_train_data))])
predicted = self.__model.predict(trX2)
plt.figure()
plt.plot(trX2, trY2, marker='.', label='組込関数')
plt.plot(trX2, predicted, marker='.', label='独自関数')
plt.legend(loc='best', fontsize=10)
plt.grid()
plt.xlabel('θ')
plt.ylabel('sin(θ)')
plt.show()
# モデルの保存
if not exists(DeepSin.modeldir):
try:
mkdir(DeepSin.modeldir)
except:
print('モデル保存フォルダの作成中にエラーが発生しました。')
print('Unexpected error:', exc_info()[0])
raise
try:
self.__model.save(DeepSin.modelfile)
except:
print('モデルの保存中にエラーが発生しました。')
print('Unexpected error:', exc_info()[0])
raise
def __sin(self, θ):
# 角度θを0.0~359.999...の範囲に直す
while True:
if θ < 0.0:
θ += 2.0 * pi
continue
if 2.0 * pi <= θ:
θ -= 2.0 * pi
continue
break
# 180度を超える場合、x軸に関して対称とする
if pi < θ:
return -1 * self.sin(2.0 * pi - θ)
# 90〜180度の場合、y軸に関して対称とする
if 0.5 * pi < θ:
return self.sin(pi - θ)
return self.__model.predict([θ])[0][0]
def sin(self, θ):
return frompyfunc(self.__sin, 1, 1)(θ)
ds = DeepSin(recycle=False)
deg = 30.0
rad = radians(deg)
x = ds.sin(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
deg = 45.0
rad = radians(deg)
x = ds.sin(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
ds = DeepSin()
deg = 60.0
rad = radians(deg)
x = ds.sin(rad)
y = sin(rad)
print("独自関数によるsin(" + str(deg) + "):" + str(x))
print("組込関数によるsin(" + str(deg) + "):" + str(y))
rads = [radians(i) for i in range(359)]
h = ds.sin(rads)
y = sin(rads)
e = absolute(y - h)
print("誤差最大値 :" + str(max(e)))
print("誤差最小値 :" + str(min(e)))
print("誤差平均値 :" + str(mean(e)))
print("誤差標準偏差:" + str(stdev(e)))
Using TensorFlow backend.
訓練を行うので、お待ちください。
Train on 300000 samples, validate on 90000 samples
Epoch 1/20
300000/300000 [==============================] - 2s 5us/step - loss: 0.0697 - val_loss: 0.0012
Epoch 2/20
300000/300000 [==============================] - 1s 3us/step - loss: 5.5763e-04 - val_loss: 2.6283e-04
Epoch 3/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.3936e-04 - val_loss: 5.4291e-05
Epoch 4/20
300000/300000 [==============================] - 1s 3us/step - loss: 2.5608e-05 - val_loss: 9.9707e-06
Epoch 5/20
300000/300000 [==============================] - 1s 3us/step - loss: 5.6591e-06 - val_loss: 4.3353e-06
Epoch 6/20
300000/300000 [==============================] - 1s 3us/step - loss: 2.4574e-06 - val_loss: 1.3504e-06
Epoch 7/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.4784e-06 - val_loss: 9.6404e-07
Epoch 8/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.1821e-06 - val_loss: 5.3071e-07
Epoch 9/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.1959e-06 - val_loss: 2.5098e-06
Epoch 10/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.2143e-06 - val_loss: 4.1867e-07
Epoch 11/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.6130e-06 - val_loss: 2.5240e-07
Epoch 12/20
300000/300000 [==============================] - 1s 3us/step - loss: 7.9917e-07 - val_loss: 5.5269e-07
Epoch 13/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.9296e-06 - val_loss: 4.3476e-07
Epoch 14/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.2812e-06 - val_loss: 2.6409e-07
Epoch 15/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.2712e-06 - val_loss: 1.9644e-07
Epoch 16/20
300000/300000 [==============================] - 1s 3us/step - loss: 2.0916e-06 - val_loss: 3.1340e-07
Epoch 17/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.1972e-06 - val_loss: 8.7616e-07
Epoch 18/20
300000/300000 [==============================] - 1s 3us/step - loss: 2.6864e-06 - val_loss: 1.4640e-05
Epoch 19/20
300000/300000 [==============================] - 1s 3us/step - loss: 4.0446e-06 - val_loss: 1.4378e-05
Epoch 20/20
300000/300000 [==============================] - 1s 3us/step - loss: 1.1424e-06 - val_loss: 1.0116e-07
独自関数によるsin(30.0):0.500035
組込関数によるsin(30.0):0.49999999999999994
独自関数によるsin(45.0):0.70708025
組込関数によるsin(45.0):0.7071067811865475
訓練済みモデルを読み込みます。
独自関数によるsin(60.0):0.86587673
組込関数によるsin(60.0):0.8660254037844386
誤差最大値 :0.00250852108001709
誤差最小値 :3.4490914585516563e-06
誤差平均値 :0.0001902273061400219
誤差標準偏差:0.0002800383029470891
さすがに、精度の点では、他のアプローチに及びませんでした。人間がコンパスと分度器と定規でsin(θ)を求める場合と比較して、どちらが精度が高いでしょうね。
なお、このプログラムは、私が書いた初めてのディープラーニングですが、完成させるまでに試行錯誤を重ねました。
- データの桁数が増えたら精度も増えるように見えたので、与えるデータ量を増やしたら、メモリがスワップアウトして、固まってしまった。
- 別の条件下では、データの桁数を増やしたところ、かえって測定結果が悪化するように見えた。
- ユニット数や中間層の数を増やせば、表現力がアップするのかと思いきや、必ずしもそうではなかった。結果を出すためには、ちょうど良いバランスを見つける必要があった。
結局のところ、サインカーブの対称性に着目し、データの範囲を0から0.5πの間にしぼることにより(=表現対象を単純化することにより)、それなりのリソース(時間、空間)で、それなりの精度が得られるようになりました。私の知識不足もあるのでしょうが、ディープラーニングの難しさを感じました。ディープラーニングの開発のマネージャーをやられている方々は、どうやってマネジメントされているんでしょうね。
そして説明可能性という点では…「そもそも、深層ニューラルネットワークは、パラメータ調整により、任意の関数を任意の精度で近似することができる。利用可能なリソースも考慮のうえ、これくらいのネットワークなら近似できるだろうという仮説を立て、パラメータを設定。実際のデータを元に訓練を実施し、完成したモデルを検証用のデータで検証してみたところ、一定程度の精度が得られたのでこれで良しとした。」といった説明しかできないように思います。これで納得してもらえるでしょうか。なかなか難しいと思いますね。LIME、SHAP、Grad-CAMなどの「説明可能性を取り戻す」仕組みの実用化が待たれます。
まとめ
機械学習という手法の登場によって、コンピュータに知能をもたせる取り組み——広義のプログラミングと言って良いかもしれない——は、大きく幅が広がりました。
演繹から帰納。論理学から統計学。思弁から経験。そのパラダイム転換に戸惑いつつも、新しい「おもちゃ」の登場に喜ぶ子どものような気分もあります。
とはいえ、喜んでばかりもいられません。二木康晴/塩野誠(2017)によれば、人工知能の法的位置付けは「当分の間、単なる道具」で、行為の責任は、設計開発者 and / or 管理利用者が負うことになるだろうとのことです。
一人の開発者としても、ツールの妥当性を説明する言葉をもたなければいけないと、痛切に感じています。その言葉はたぶん、統計学の言葉なんだろうなと思いつつ、この駄文に終止符を打つことにします。ここまで読んでくださる方、いるのかな。