巡回セールスマン問題の近似解法, 発見的解法として 最近傍法, 2-opt, Lin-Kernighan, Lin-Kernighan-Helsgaun (general k-opt) を紹介したいと思います。
言語はわかりやすく Python として、Numpy や NetworkX を最大限活用した実装を行います。
【使用したコードはこちらから】
【使用した図はこちらから】
いずれもご自由にダウンロードしていただいて構いません。
1. 巡回セールスマン問題(TSP)とは
各 $n$ 頂点を 1 度だけ訪問するような最短の巡回路を求める問題です。
問題が座標点を与えるなら例えば points = [(x0, y0), (x1, y1), ...] のような頂点リストがあって、tour = [0, 3, 1, 5, ...] のような points に対する訪問順 tour のうち最適なものが欲しいということになります。
(座標点ではなく重み付き辺集合を与える問題もあります)
2. TSPLIB の導入
TSPLIB で TSP の問題例を入力してみましょう。
今回解くのは symmetric traveling salesman problem (TSP) の問題です。
ALL_tsp.tar.gz をダウンロードして適当な場所に展開してください。
最適解のファイルがまったく足りていないため、私は ALL_tsp に https://github.com/mathinking/HopfieldNetworkToolbox/tree/master/data/TSPFiles/TSPTours を追加して使用しています。
データ入力
とりあえず色々インポートしておいて
import gzip
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import time
import random
import itertools
from functools import cache
from numba import njit
from scipy.spatial import KDTree, Delaunay
import networkx as nx
import cProfile
グローバルに使うものを置いておきます。
target_file = ''
n = 0
points = []
tour = []
optimal_tour = []
seed = None
早速データセットを読み込んでみましょう。
def read_points():
global points, n
# Google Colab で Google Drive を使う場合
source_file = "/content/drive/MyDrive/ALL_tsp/" + target_file + ".tsp.gz"
with gzip.open(source_file, 'rt') as gzip_file:
contents = [s.strip() for s in gzip_file.read().strip().split('\n')]
contents = contents[contents.index('NODE_COORD_SECTION') + 1:]
if contents[-1] == 'EOF':
contents = contents[:-1]
points = np.array([[float(x) for x in l.split()[1:]] for l in contents])
n = len(points)
target_file = 'berlin52'
read_points()
print(points.tolist())
points は 2次元座標の配列になります。
>> [[565.0, 575.0], [25.0, 185.0], [345.0, 750.0], [945.0, 685.0], [845.0, 655.0], [880.0, 660.0], [25.0, 230.0], [525.0, 1000.0], [580.0, 1175.0], [650.0, 1130.0], [1605.0, 620.0], [1220.0, 580.0], [1465.0, 200.0], [1530.0, 5.0], [845.0, 680.0], [725.0, 370.0], [145.0, 665.0], [415.0, 635.0], [510.0, 875.0], [560.0, 365.0], [300.0, 465.0], [520.0, 585.0], [480.0, 415.0], [835.0, 625.0], [975.0, 580.0], [1215.0, 245.0], [1320.0, 315.0], [1250.0, 400.0], [660.0, 180.0], [410.0, 250.0], [420.0, 555.0], [575.0, 665.0], [1150.0, 1160.0], [700.0, 580.0], [685.0, 595.0], [685.0, 610.0], [770.0, 610.0], [795.0, 645.0], [720.0, 635.0], [760.0, 650.0], [475.0, 960.0], [95.0, 260.0], [875.0, 920.0], [700.0, 500.0], [555.0, 815.0], [830.0, 485.0], [1170.0, 65.0], [830.0, 610.0], [605.0, 625.0], [595.0, 360.0], [1340.0, 725.0], [1740.0, 245.0]]
最適解も入力してみましょう。
def read_optimal_tour():
global optimal_tour
source_file = "/content/drive/MyDrive/ALL_tsp/" + target_file + ".opt.tour"
with open(source_file, 'r') as file:
contents = [s.strip() for s in file.read().strip().split('\n')]
contents = contents[contents.index('TOUR_SECTION') + 1:]
if contents[-1] == 'EOF':
contents = contents[:-1]
if contents[-1] == '-1':
contents = contents[:-1]
optimal_tour = np.array([int(l) - 1 for l in contents])
target_file = 'berlin52'
read_optimal_tour()
print(optimal_tour.tolist())
訪問順が 0 以上 $n$ 未満の整数の配列で表されます。
>> [0, 48, 31, 44, 18, 40, 7, 8, 9, 42, 32, 50, 10, 51, 13, 12, 46, 25, 26, 27, 11, 24, 3, 5, 14, 4, 23, 47, 37, 36, 39, 38, 35, 34, 33, 43, 45, 15, 28, 49, 19, 22, 29, 1, 6, 41, 20, 16, 2, 17, 30, 21]
可視化
今後のために matplotlib.pyplot で可視化しておきましょう。
def plot_points():
plt.scatter(*points.T)
def plot_tour():
plt.plot(*points[np.append(tour, tour[0])].T, 'k')
plt.scatter(x, y), plt.plot(x, y) は各点の x 座標のみ, y 座標のみのリストを受け取るので、x, y = points.T を渡せばいいですね。.T は転置です。
\begin{aligned}
\mathrm{points} &= \begin{bmatrix}
\,[x_0, y_0] \\
\,[x_1, y_1] \\
\,\vdots
\end{bmatrix}\\
\mathrm{points}^\mathsf{T} &= \begin{bmatrix}
\,[x_0, x_1, \cdots]\\
\,[y_0, y_1, \cdots]
\end{bmatrix} = \begin{bmatrix}
\,\boldsymbol{x}\, \\
\,\boldsymbol{y}\,
\end{bmatrix}
\end{aligned}
tour は points のインデックスなので単に points[tour] とできます。ただし tour[n-1] → tour[0] の辺もプロットするため np.append で tour[0] を tour の末尾に追加しています。線の色は 'k' (黒) を選択。
target_file = 'berlin52'
read_points()
read_optimal_tour()
tour = optimal_tour
plt.figure(dpi=300)
plot_points()
plot_tour()
plt.show()

近似解の評価
近似解の評価指標として、現在の tour による巡回路長を最適解の tour による巡回路長で割った「近似率」を利用することにします。
def length(tour):
return np.linalg.norm(points[tour] - points[np.roll(tour, -1)], axis=1).sum()
def approx_ratio():
return length(tour) / length(optimal_tour)
def plot_approx_ratio():
plt.xlabel(f'approx_ratio = {approx_ratio():.3f}', labelpad=10, fontsize=12)
np.roll(tour, -1) は tour を左に 1 つ巡回シフトします。
[0, 1, 2, 3] を np.roll して
[1, 2, 3, 0] を得るように。
この 2 つの各列は [0, 1], [1, 2], [2, 3], [3, 0] と巡回路 $0→1→2→3→0$ の各辺のインデックスになっていますね。シフト前が各左端点でシフト後が各右端点です。あとはそれぞれを points に与えて両端点の差のノルムを取れば各辺長が得られるというわけです。最後に .sum() で巡回路長が返ります。
plot_approx_ratio は $x$ 軸のラベルでもお借りして表示することにしましょう。
3. 近似解法の実装
最近傍法
最近傍法 (nearest neighbor algorithm) は最も単純な近似解法の一つです。
初期点 start に対し tour = [start] から始め、次の点を未探索の最も近い点として tour へ追加していきます。ここでは start をランダムに選ぶことにしましょう。
def nearest_neighbor():
rng = np.random.default_rng(seed)
start = rng.integers(n)
tour = [start]
visited = np.zeros(n, dtype=bool)
visited[start] = True
for _ in range(n - 1):
node = tour[-1]
distances = np.linalg.norm(points - points[node], axis=1)
distances[visited] = np.inf
next_node = np.argmin(distances)
tour.append(next_node)
visited[next_node] = True
return np.array(tour)
rng = np.random.default_rng(seed) は Numpy の乱数生成器です。
start = rng.integers(n) とすることで 0 以上 $n$ 未満の整数から一つ選んで start を決めています。
visited は各頂点が訪問済みかどうかを保持します。
現在の tour の末尾 node = tour[-1] に最も近い未探索の点を探すため、node と各点との距離 distances を計算し、かつ distances[visited] = np.inf で訪問済みの点との距離を ∞ にしておきます。
すると next_node = np.argmin(distances) で探していたものが求まったので tour に追加していって完成です。
試してみましょう。
target_file = 'berlin52'
read_points()
read_optimal_tour()
seed = 0
tour = nearest_neighbor()
print(tour.tolist())
print(approx_ratio())
>> [44, 18, 40, 7, 9, 8, 42, 14, 4, 23, 47, 37, 39, 36, 38, 35, 34, 33, 43, 45, 15, 49, 19, 22, 30, 17, 21, 0, 48, 31, 2, 16, 20, 29, 28, 24, 3, 5, 11, 27, 26, 25, 46, 12, 13, 51, 10, 50, 32, 41, 6, 1]
>> 1.2979405848087036
seed = 0 で 近似率は 1.298 くらいですね。
seed = None とすれば毎回ランダムな初期点になります。
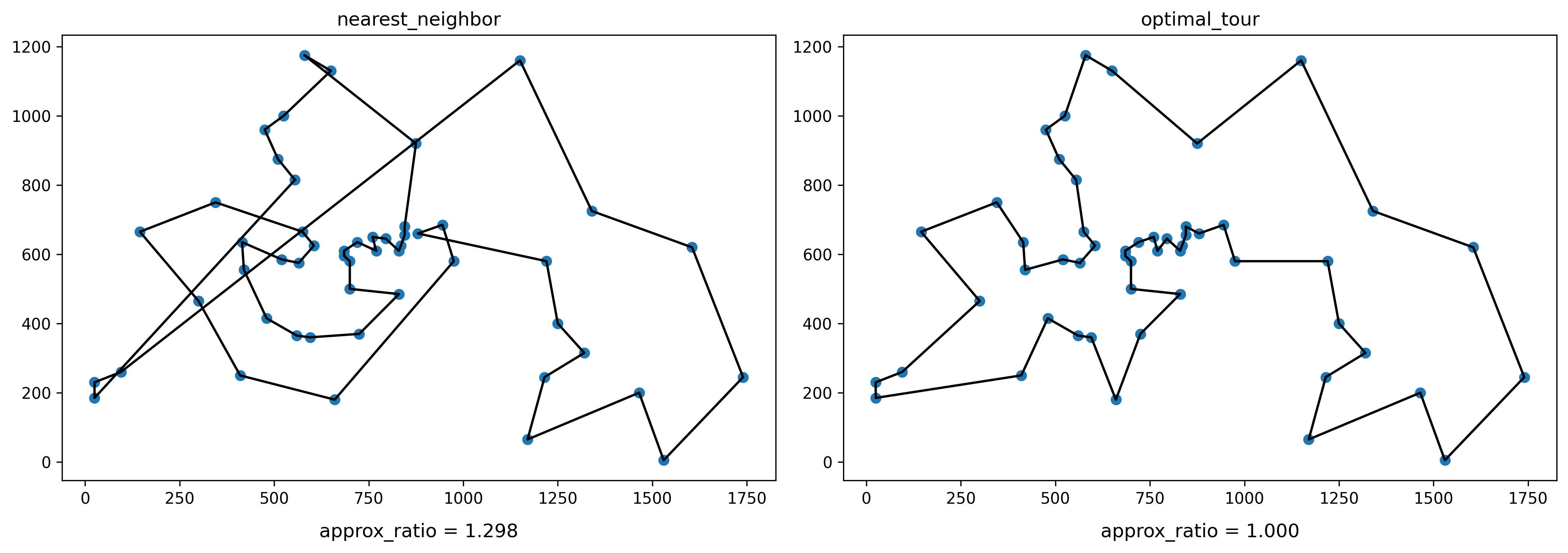
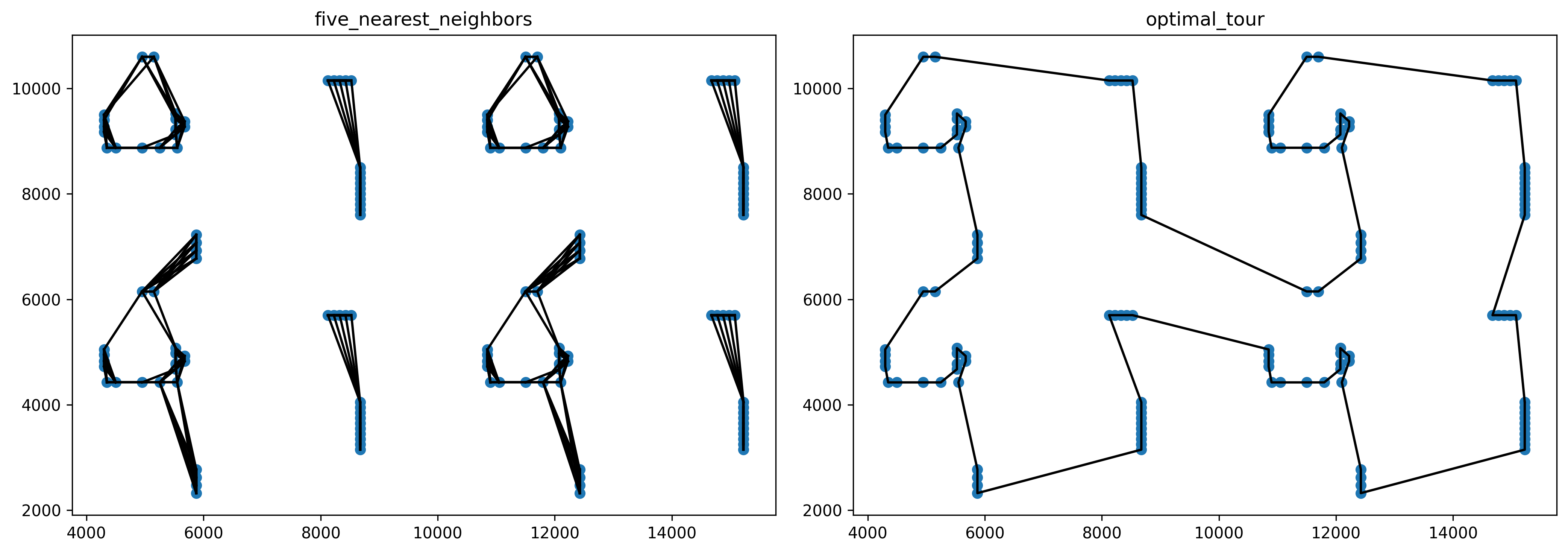
最適解とも見比べてみましょう。
plt.figure(figsize=(7 * 2, 5), dpi=300)
tour = nearest_neighbor()
plt.subplot(1, 2, 1)
plt.title('nearest_neighbor')
plot_points()
plot_tour()
plot_approx_ratio()
tour = optimal_tour
plt.subplot(1, 2, 2)
plt.title('optimal_tour')
plot_points()
plot_tour()
plot_approx_ratio()
plt.tight_layout()
plt.show()
plt.subplot(行数, 列数, インデックス) で複数の図を同時にプロットできます。
最適解と全く同じ部分もある一方で非常に長い横断辺が確認できますね。
2-opt
2-opt は局所探索法の一つであり、現在の解の改善解を見つけるアルゴリズムです。
2-opt はどのように改善解を見つけるかというと、巡回路中の 2 辺を削除して新たに 2 辺を追加するといった操作を行います。ですから 3-opt, 4-opt, 5-opt, ... なんていうのも同様に考えられますね。
(事実 5-opt はとても優秀で、後の Lin-Kernighan, Lin-Kernighan-Helsgaun アルゴリズムにも登場します)
まずはもっともシンプルな 2-opt を見ていきましょう。
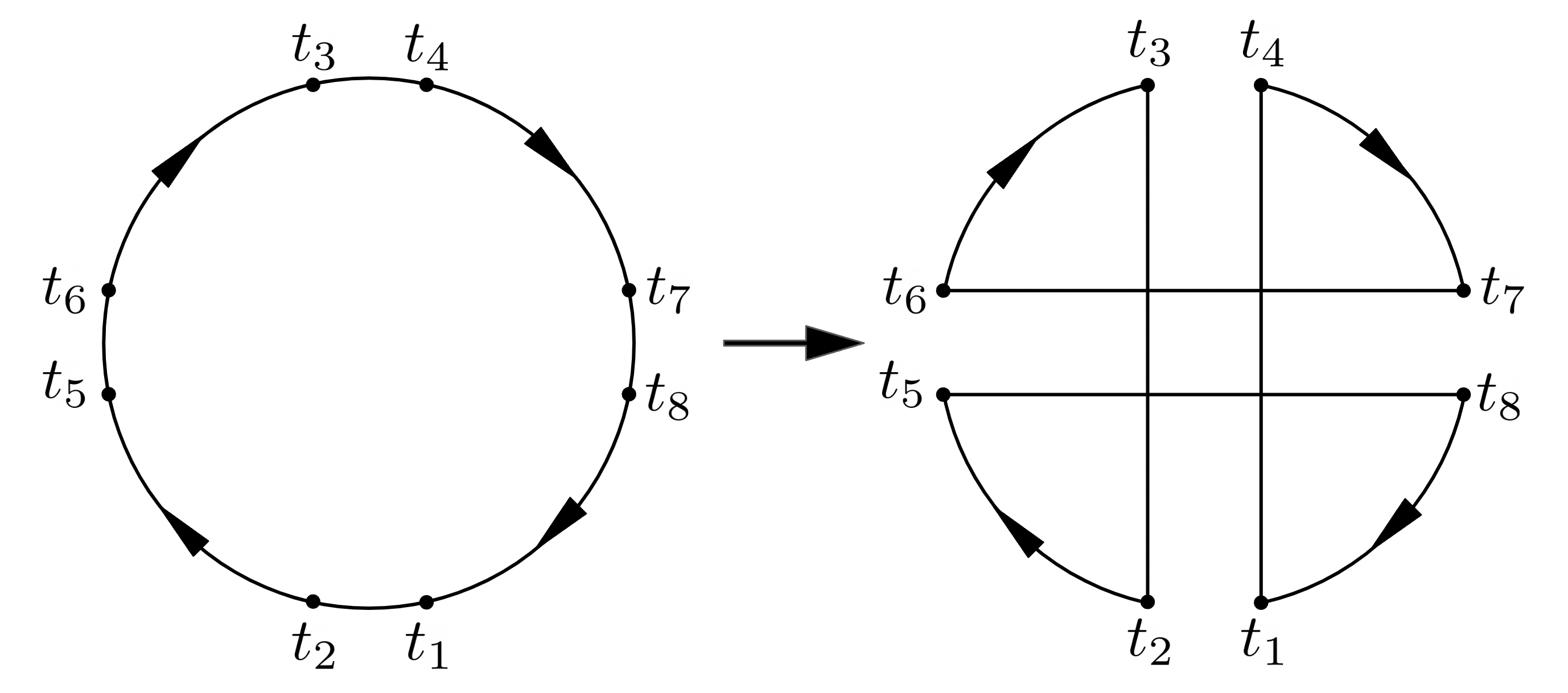
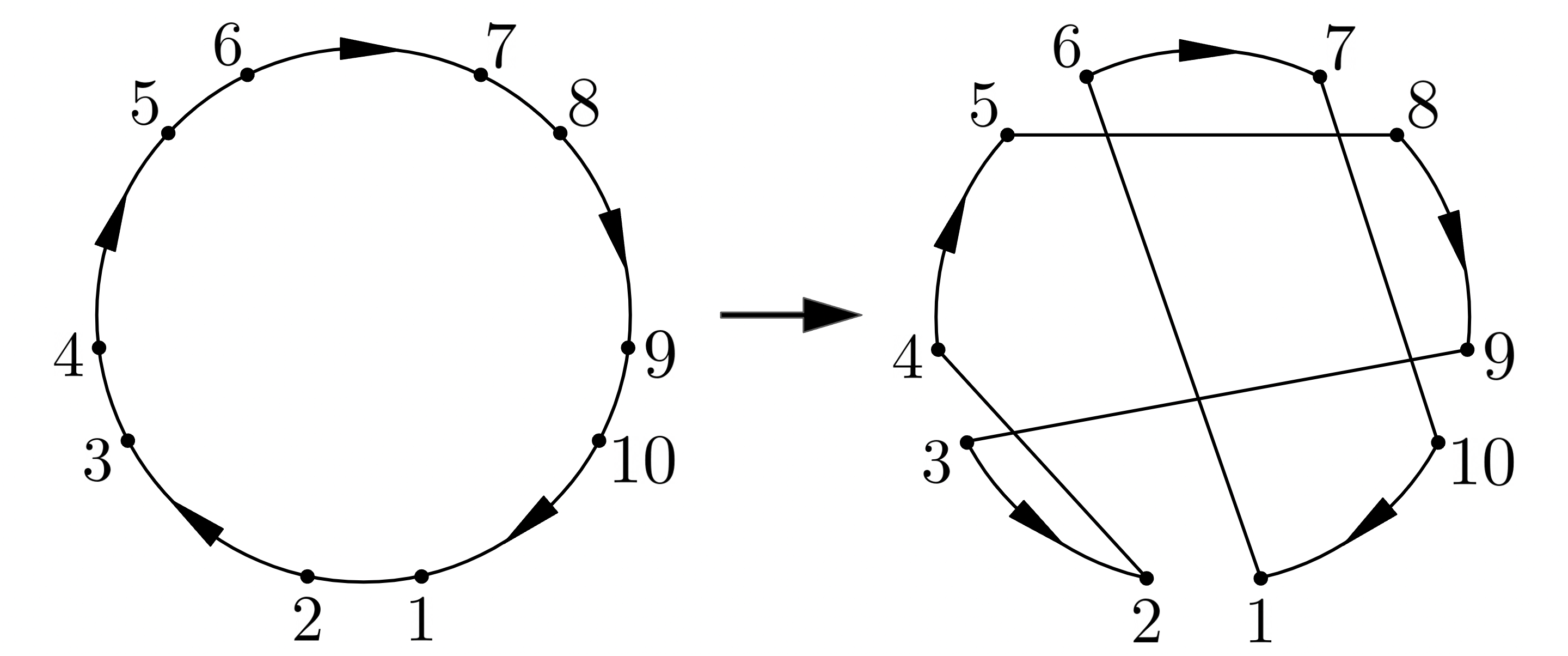
上図のように巡回路上で点 $t_1, t_2, t_3, t_4$ を選びます。このとき 辺 $[t_1, t_2]$ を削除, $[t_2, t_3]$ を追加, $[t_3, t_4]$ を削除, $[t_4, t_1]$ を追加 としましょう。この手順によって 2 辺の交換が達成できました。このように削除と追加を交互に行う辺の交換は sequential であるといいます。
さて $\mathrm{tour}$ はどのように変化するでしょうか。交換前は $$\mathrm{tour}[t_1] → \mathrm{tour}[t_2] → \cdots → \mathrm{tour}[t_4] → \mathrm{tour}[t_3] → \cdots → \mathrm{tour}[t_1]$$ といった訪問順でしたが、交換後は $$\mathrm{tour}[t_1] → \mathrm{tour}[t_4] → \cdots → \mathrm{tour}[t_2] → \mathrm{tour}[t_3] → \cdots → \mathrm{tour}[t_1]$$ となっていますね。交換前後で $\mathrm{tour}[t_2]\ 〜\ \mathrm{tour}[t_3]$ ($\mathrm{tour}[t_3]$ を含まない) が逆順になっただけのようです。
これなら tour[t2:t3] = tour[t2:t3][::-1] で実行できます。
交換後の巡回路が改善解になるかは「削除する総辺長 - 追加する総辺長」が正かどうかで判定できます。この値は gain (利得) と呼ばれます。
以上を踏まえて 2-opt 法を実装しましょう。
@njit(cache=True)
def point_dist(p, q):
return np.linalg.norm(p - q)
def dist(ta, tb):
return point_dist(points[tour[ta]], points[tour[tb]])
def two_opt():
rng = np.random.default_rng(seed)
def step():
for t1 in rng.permutation(np.arange(n)):
t2 = (t1 + 1) % n
for t3 in rng.permutation(np.arange(t2 + 2, n)):
t4 = (t3 - 1) % n
gain = dist(t1, t2) - dist(t2, t3) + dist(t3, t4) - dist(t4, t1)
if gain > 0:
tour[t2:t3] = tour[t2:t3][::-1]
return True
return False
while step():
pass
return tour
まず $\mathrm{tour}$ 上の 2 点 $t_a, t_b$ の距離を返す dist(ta, tb) を定義しています。@njit は高速化のおまじないです。
本題の two_opt 関数は step() で 2-opt による解の改善を行います。これ以上改善できなかった場合 step() が False を返すことで無限ループが終了する形を取りました。
step では配列をシャッフルする rng.permutation によって $t_1, t_3$ をランダムに選び、先に挙げた図の通り $t_2 = t_1 + 1,\ t_4 = t_3 - 1$ を求めています。ただし $n - 1 \leftrightarrow 0$ が隣り合っていないといけないので $n$ で割ったあまりが付いています。
あとは gain が正のとき tour を改善すれば完成です。
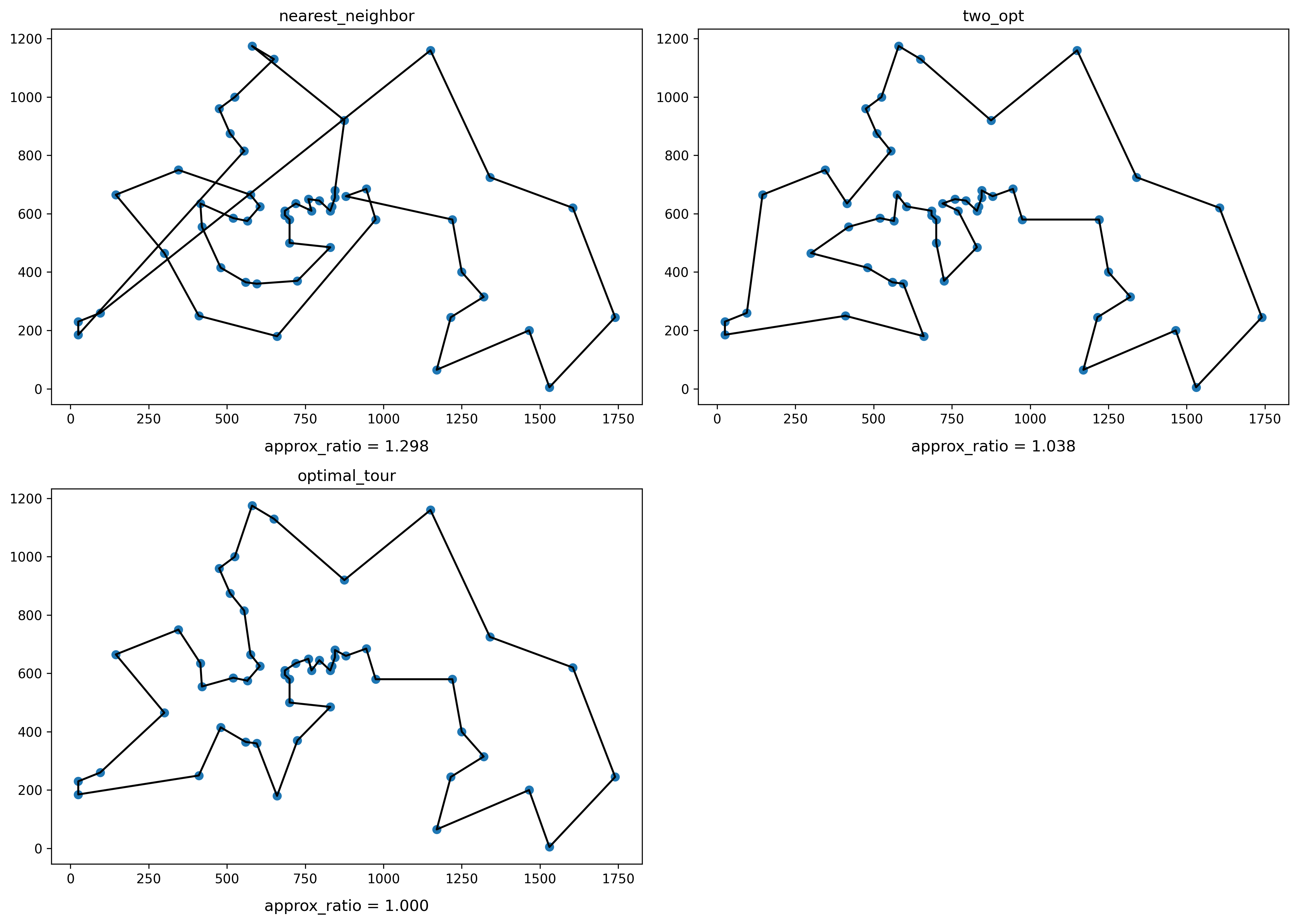
試してみましょう。
target_file = 'berlin52'
read_points()
read_optimal_tour()
plt.figure(figsize=(7 * 2, 5 * 2), dpi=300)
seed = 0
tour = nearest_neighbor()
plt.subplot(2, 2, 1)
plt.title('nearest_neighbor')
plot_points()
plot_tour()
plot_approx_ratio()
tour = two_opt()
plt.subplot(2, 2, 2)
plt.title('two_opt')
plot_points()
plot_tour()
plot_approx_ratio()
tour = optimal_tour
plt.subplot(2, 2, 3)
plt.title('optimal_tour')
plot_points()
plot_tour()
plot_approx_ratio()
plt.tight_layout()
plt.show()
最近傍法に比べてずっと最適解に近いものが得られました。
Lin-Kernighan Algorithm
『An Effective Heuristic Algorithm for the Traveling-Salesman Problem』(S. Lin & B. W. Kernighan, 1973) による解法です。
Lin-Kernighan アルゴリズムは 2-opt と同じ局所探索法ですが、動的 k-opt によって改善解を探索します。また追加する辺もあらかじめ用意した候補集合から選ぶことにしました。一度に多くの辺を交換できることから探索パフォーマンスが向上しただけでなく、計算量も抑える工夫が盛り込まれています。
Candidate Set
動的 k-opt は複雑なので、先に追加辺の候補集合を作成してみましょう。
Lin, Kernighan は候補集合に "five nearest neighbors" を用いました。要するに辺 $[t_1, t_2]$ を削除, $[t_2, t_3]$ を追加... とするときの $t_3$ は $t_2$ にもっとも近い 5 点のみから選ぶとしたのです。追加辺が長すぎれば改善解が得られる見込みはほとんどないので、この設定は合理的と言えます。
このような集合は kd-tree を使えば簡単に作成できます。
def five_nearest_neighbors_graph():
tree = KDTree(points)
return np.array([tree.query(p, k=6)[1][1:] for p in points])
Python には scipy.spatial.KDTree があるので簡単ですね。
tree.query(p, k=6) で 点 p の近隣 6 点 (点 p 自身を含む) との距離, およびその 6 点のインデックスが近い順で返ってきます。距離は今いらないので [1] でアクセスして、点 p 自身もいらないので更に [1:] でアクセスすれば、求めていた "five nearest neighbors" の完成です。
target_file = 'berlin52'
read_points()
read_optimal_tour()
candidate_set = five_nearest_neighbors_graph()
print(candidate_set.tolist())
>> [[21, 48, 31, 34, 35], [6, 41, 29, 20, 16], [17, 18, 30, 16, 44], [5, 14, 4, 24, 23], [14, 23, 5, 47, 37], [4, 14, 23, 3, 47], [1, 41, 20, 29, 16], [40, 18, 9, 8, 44], [9, 7, 40, 18, 44], [8, 7, 40, 18, 42], [50, 11, 51, 26, 27], [27, 50, 24, 26, 3], [26, 13, 25, 51, 27], [12, 51, 46, 26, 25], [4, 5, 23, 37, 47], [49, 43, 45, 19, 28], [2, 20, 17, 30, 21], [30, 21, 2, 0, 31], [44, 40, 7, 2, 31], [49, 22, 15, 29, 43], [30, 22, 17, 29, 21], [0, 48, 31, 30, 17], [19, 49, 30, 21, 29], [47, 4, 37, 14, 5], [3, 5, 23, 47, 4], [26, 27, 46, 12, 11], [27, 25, 12, 11, 46], [26, 25, 11, 12, 24], [49, 15, 19, 29, 22], [22, 19, 49, 20, 28], [17, 21, 0, 20, 22], [48, 0, 21, 35, 34], [42, 50, 9, 3, 5], [34, 35, 38, 36, 43], [35, 33, 38, 48, 36], [34, 33, 38, 48, 39], [39, 37, 38, 47, 23], [39, 36, 23, 47, 4], [39, 35, 34, 36, 33], [37, 36, 38, 23, 47], [7, 18, 44, 8, 9], [6, 1, 20, 29, 16], [14, 3, 5, 4, 37], [33, 34, 35, 36, 45], [18, 31, 40, 7, 48], [47, 43, 36, 23, 15], [25, 26, 12, 27, 13], [23, 4, 37, 36, 5], [31, 0, 35, 34, 21], [19, 22, 15, 43, 28], [11, 10, 27, 24, 3], [12, 13, 10, 26, 27]]
points[0] に近い点は points[21], points[48], ... だそうです。
candidate_set と最適解を見比べてみましょう。
def plot_candidate_set_graph():
plt.plot(*points[[(i, j) for i, candidates in enumerate(candidate_set) for j in candidates]].T, 'k')
target_file = 'berlin52'
read_points()
read_optimal_tour()
plt.figure(figsize=(7 * 2, 5), dpi=300)
candidate_set = five_nearest_neighbors_graph()
plt.subplot(1, 2, 1)
plt.title('five_nearest_neighbors')
plot_points()
plot_candidate_set_graph()
tour = optimal_tour
plt.subplot(1, 2, 2)
plt.title('optimal_tour')
plot_points()
plot_tour()
plt.tight_layout()
plt.show()
berlin52 では最適解を完全に含んでいることが分かります。
もちろん一般には最適解の辺を取りこぼすこともあり、Lin-Kernighan-Helsgaun ではさらに候補集合を最適解に近づける工夫が盛り込まれます。
では早速 candidate_set を 2-opt に組み込んでみましょう。
def two_opt_lk():
rng = np.random.default_rng(seed)
def step():
tour_index = np.argsort(tour)
for t1 in rng.permutation(np.arange(n)):
t2 = (t1 + 1) % n
for t3 in tour_index[candidate_set[tour[t2]]]:
t4 = (t3 - 1) % n
gain = dist(t1, t2) - dist(t2, t3) + dist(t3, t4) - dist(t4, t1)
if gain > 1e-9:
t2, t3 = sorted((t2, t3))
tour[t2:t3] = tour[t2:t3][::-1]
return True
return False
while step():
pass
return tour
追加辺 $[t_2, t_3]$ の $t_3$ を候補集合から選ぶように変更するだけですね。
ただし candidate_set は points のインデックスを返すので、tour のインデックスに直す tour_index = np.argsort(tour) を被せています。ソートを使ってしまうと無駄に $O(n\log n)$ かかりますが、ここでは Numpy を用いる分高速です。
Variable k-opt
さて、Lin-Kernighan アルゴリズムの肝となる動的 k-opt に話を移しましょう。
まず k-opt は単に 2-opt の拡張と考えられます。要するに k-opt では 辺 $[t_1, t_2]$ を削除, $[t_2, t_3]$ を追加, $\cdots$, $[t_{2k-1}, t_{2k}]$ を削除, $[t_{2k}, t_1]$ を追加 といった感じで辺の交換を K 回行います。簡単ですね。
問題はそのような $\boldsymbol{t} = [t_1, t_2, \cdots, t_{2k-1}, t_{2k}]$ が実行不可能な場合を判定しなくてはならないことにあります。
実は話の都合上省略しましたが、2-opt にも実行不可能な場合があるのです。それは $t_4 = t_3 - 1$ を $t_4 = t_3 + 1$ にすると観察できます。
上図は 2 辺を交換しているので 2-opt にこそなってはいますが、巡回路が 2 つに分かれてしまっています。したがって tour 上で交換を実現できないため実行不可能となるわけです。
実行可能かどうかは交換後のグラフが閉路グラフ(連結グラフであり、かつすべての頂点の次数が 2 であるようなグラフ)になっているかで確かめられます。
$\boldsymbol{t} = [t_1, t_2, t_3, t_4, ...]$ のとき 削除辺は $[t_1, t_2], [t_3, t_4], \cdots$ となり、追加辺は $[t_2, t_3], \cdots, [t_{2k}, t_1]$ となるのでした。このリストをそれぞれ $X, Y$ と置きます。
X = t.reshape(-1, 2)
Y = np.roll(t, -1).reshape(-1, 2)
このとき交換後のグラフ $G$ は $\boldsymbol{t}$ の各頂点に対する閉路グラフに $Y$ を足して $X$ を引けば簡単に得られますね。
G = nx.cycle_graph(np.unique(t), nx.MultiGraph)
G.add_edges_from(Y)
G.remove_edges_from(X)
これで $\boldsymbol{t}$ が実行可能かどうか判定する準備が整いました。
def feasible(t):
X = t.reshape(-1, 2)
Y = np.roll(t, -1).reshape(-1, 2)
G = nx.cycle_graph(np.unique(t), nx.MultiGraph)
G.add_edges_from(Y)
G.remove_edges_from(X)
return nx.is_connected(G) and all(d == 2 for _, d in G.degree)
feasible 関数はこのままだと深刻なボトルネックになるので、計算結果をキャッシュする機能も付けておきましょう。$\boldsymbol{t}$ を座標圧縮したものをキーとして、判定済みの $\boldsymbol{t}$ を記憶しておきます。
feasible_cache = dict()
def feasible(t):
unique_t, compressed_t = np.unique(t, return_inverse=True)
key = compressed_t.tobytes()
if key in feasible_cache:
return feasible_cache[key]
... # 省略
result = nx.is_connected(G) and all(d == 2 for _, d in G.degree)
feasible_cache[key] = result
return result
座標圧縮とは次のような操作をいいます。
\begin{aligned}
\boldsymbol{t} &= [297, 500, 816, 1023, 500, 2392]\\
\mathrm{compress}(\boldsymbol{t}) &= [0, 1, 2, 3, 1, 4]
\end{aligned}
各要素が全体の中で何番目に小さいかを求めることで、$\boldsymbol{t}$ の最も単純な形式が得られました。この圧縮後の $\boldsymbol{t}$ について feasible の結果をキャッシュしておけば、圧縮後がその形式に当てはまる他の任意の $\boldsymbol{t}$ について feasible を再計算せずに済みます。
Python では np.unique(t, return_inverse=True) で簡単に座標圧縮できて便利ですね。
また $\boldsymbol{t}$ が実行可能であったとき 交換後のグラフ $G$ は改善解を得る重要な手がかりにもなります。改善解を得るには下図に示される $G$ の円弧の各辺(交換前の巡回路のパス)をどの順にどの向きで移動すべきか知る必要があるためです。
各端点に接続する辺を移動する際の方向として $+1, -1$ をそれぞれ割り当ててみました。これを direction として定義し、この方向とセットにしたパスを順路と呼ぶことにします。
feasible(t) で $\boldsymbol{t}$ が実行可能であった場合、その順路 route をグローバルに保存しておくことにしましょう。
route = None
feasible_cache = dict()
def feasible(t):
global route
unique_t, compressed_t = np.unique(t, return_inverse=True)
key = compressed_t.tobytes()
if key in feasible_cache:
if (cached_route := feasible_cache[key]) is None:
return False
route_path, route_direction = cached_route
route = np.c_[unique_t[route_path], route_direction]
return True
X = compressed_t.reshape(-1, 2)
Y = np.roll(compressed_t, -1).reshape(-1, 2)
G = nx.cycle_graph(u := unique_t.size, nx.MultiGraph)
G.add_edges_from(Y)
G.remove_edges_from(X)
if not (nx.is_connected(G) and all(d == 2 for _, d in G.degree)):
feasible_cache[key] = None
return False
X = nx.from_edgelist(X)
Y = nx.from_edgelist(Y)
tail, init = max(G.edges & Y.edges)
G.remove_edge(tail, init)
route_path = []
is_path = True
for a, b in nx.dfs_edges(G, source=init):
if is_path:
if b not in [(a - 1) % u, (a + 1) % u] or (a, b) in X.edges:
route_path.append([a, a])
continue
route_path.append([a, b])
is_path = not is_path
if is_path:
route_path.append([tail, tail])
route_path = np.array(route_path)
route_direction = np.sign(np.diff(route_path, axis=1))
route_direction[np.all(route_path == [0, u - 1], axis=1)] = -1
route_direction[np.all(route_path == [u - 1, 0], axis=1)] = 1
feasible_cache[key] = [route_path, route_direction]
route = np.c_[unique_t[route_path], route_direction]
return True
深さ優先探索順に $G$ の各辺を取り出し、一つおきに route_path へ追加していきます。最初に取り出される辺が円弧の辺になるよう、追加辺 [tail, init] を選んで削除し init から深さ優先探索を走らせていることに注意してください。
途中で円弧の辺として自己ループ辺を追加する場合分けは次のような特殊ケースに対応するためです。
ここで route_path は $[(t_5, t_4), (t_2, t_2), (t_3, t_1)]$ の形になっていなくてはいけません。
route_direction は route_path の階差の符号を取るだけです。ただし辺 [0, u - 1], [u - 1, 0] については符号を逆転させなくてはいけません。u で割ったあまりで巡回していますからね。
たとえば実行可能な 2-opt の例を入力すると次のような順路が得られます。
print(feasible([1, 2, 4, 3]))
print(route)
>> True
>> [[ 1 4 -1]
[ 2 3 1]]
ちゃんと下図に一致しています。
次のような 4-opt でも試してみると
print(feasible([1, 2, 5, 6, 8, 7, 3, 4]))
print(route)
>> True
>> [[ 3 2 -1]
[ 5 4 -1]
[ 1 8 -1]
[ 6 7 1]]
確かに実行可能な $\boldsymbol{t}$ の順路を得ることができました。
feasible_cache を埋めるために 5-opt までの $\boldsymbol{t}$ を全通り実行しておきましょう。
n = 10
for t1 in np.arange(n):
for t2 in [(t1 - 1) % n, (t1 + 1) % n]:
for t3 in np.arange(n):
if t3 in [(t2 - 1) % n, t2, (t2 + 1) % n]:
continue
for t4 in [(t3 - 1) % n, (t3 + 1) % n]:
feasible([t1, t2, t3, t4])
for t5 in np.arange(n):
if t5 in [(t4 - 1) % n, t4, (t4 + 1) % n]:
continue
for t6 in [(t5 - 1) % n, (t5 + 1) % n]:
feasible([t1, t2, t3, t4, t5, t6])
for t7 in np.arange(n):
if t7 in [(t6 - 1) % n, t6, (t6 + 1) % n]:
continue
for t8 in [(t7 - 1) % n, (t7 + 1) % n]:
feasible([t1, t2, t3, t4, t5, t6, t7, t8])
for t9 in np.arange(n):
if t9 in [(t8 - 1) % n, t8, (t8 + 1) % n]:
continue
for t10 in [(t9 - 1) % n, (t9 + 1) % n]:
feasible([t1, t2, t3, t4, t5, t6, t7, t8, t9, t10])
さて、次は route をもとに解の改善を行うことを考えていきます。
順路の各パスは $\boldsymbol{t}$ の端点で表されているため、改善解を tour 上で表現するにはその線形補間が必要になります。
\begin{aligned}
\left[10, 20, 1\right] &\rightarrow [10, 11, 12, \cdots, 20]\\
\left[10, 20, -1\right] &\rightarrow [10, 9, 8, \cdots, 0, -1, -2, \cdots, 20 - n]\\
\left[20, 10, 1\right] &\rightarrow [20, 21, 22, \cdots, n - 1,\ n,\ n + 1, \cdots, n + 10]\\
\left[20, 10, -1\right] &\rightarrow [20, 19, 18, \cdots, 10]\\
\end{aligned}
上は端点が $10, 20$ となるようなすべての順路の例について線形補間を行ったものです。$n$ で割った余りを考えれば、その結果が $10, 20$ の間のインデックスを補ったものになっていると分かります。
feasible によって得られた順路を補間して、その通りに tour を並び替えれば改善解の完成です。
def interpolate(a, b, d):
if d != np.sign(b - a):
b += d * n
d += not d
return np.arange(a, b + d, d) % n
def move():
tour[:] = tour[[ti for ta, tb, d in route for ti in interpolate(ta, tb, d)]]
最後に "double-bridge" と呼ばれる non-sequential 4-opt を実装しておきます。
これまで見てきた k-opt はすべて $\boldsymbol{t} = [t_1, t_2, t_3, t_4, \cdots]$ にしたがって削除辺と追加辺が交互に現れる、sequential なものでした。そのため更なる改善に non-sequential な交換が必要な状況ですぐさま局所最適解に陥ってしまいます。
Lin, Kernighan はこれに対処する方法として、sequential k-opt による改善に失敗した場合、特殊な non-sequential 4-opt である double-bridge による改善を行うことにしました。
上図は $\boldsymbol{t} _{(1)} = [t_1, t_2, t_3, t_4], \boldsymbol{t} _{(2)} = [t_5, t_6, t_7, t_8]$ による double-bridge を表したものです。$\boldsymbol{t} _{(1)}, \boldsymbol{t} _{(2)}$ のそれぞれは実行不可能な 2-opt ですが、それらを組み合わせることで実行可能解を得ることができています。
def double_bridge():
rng = np.random.default_rng(seed)
tour_index = np.argsort(tour)
for t1 in rng.permutation(np.arange(-1, n - 7)):
t2 = t1 + 1
for t3 in tour_index[candidate_set[tour[t2]]]:
if t3 <= t2 or t3 >= n - 3:
continue
t4 = t3 + 1
gain1 = dist(t1, t2) - dist(t2, t3) + dist(t3, t4) - dist(t4, t1)
if gain1 < 0:
continue
for t5 in rng.permutation(np.arange(t2 + 1, t3 - 1)):
t6 = t5 + 1
for t7 in tour_index[candidate_set[tour[t6]]]:
if t7 <= t4 or t7 >= n - 1:
continue
t8 = t7 + 1
gain2 = dist(t5, t6) - dist(t6, t7) + dist(t7, t8) - dist(t8, t5)
if gain1 + gain2 > 1e-9:
tour[:] = np.concatenate((tour[t8:], tour[:t2], tour[t4:t8], tour[t6:t4], tour[t2:t6]))
return True
return False
これでようやく Lin-Kernighan アルゴリズムを実装する準備が整いました。
要点は以下の通りです。
- 正の
gainをもつ実行可能な $\boldsymbol{t} = [t_1, t_2, t_3, t_4, \cdots]$ により解の改善を行う - $t_1$ をランダムに選択し、$t_2$ を $t_1 + 1, t_1 - 1$ から選ぶ
- $t_3$ を $t_2$ にもっとも近い 5 点から順に選ぶ
- ここまでの
gainを計算し、負なら この $t_3$ をスキップする- $t_4$ を $t_3 - 1, t_3 + 1$ から選ぶ
- ここまでの
gainを計算し、覚えておく
- $t_3, t_4$ を
gainが大きかった順に並び替えて再度選ぶ- 追加辺 $[t_4, t_1]$ で閉じた際に
gainが正かつ実行可能なら解を改善する - $t_5$ を $t_4$ にもっとも近い 5 点から順に選ぶ
- $\cdots$以降 繰り返し
- 追加辺 $[t_4, t_1]$ で閉じた際に
- 以上の sequential k-opt で改善に失敗した場合は double-bridge により改善を試みる
- どちらも改善失敗した時点で無限ループを抜けて終了する
def lin_kernighan():
rng = np.random.default_rng(seed)
dtype = [('ta', np.int32), ('tb', np.int32), ('gain', np.float64)]
def kopt():
tour_index = np.argsort(tour)
for t1 in rng.permutation(n):
for t2 in [(t1 + 1) % n, (t1 - 1) % n]:
t3t4gain4 = []
for t3 in tour_index[candidate_set[tour[t2]]]:
if t3 in [(t2 - 1) % n, (t2 + 1) % n]:
continue
gain3 = dist(t1, t2) - dist(t2, t3)
if gain3 < 0:
continue
for t4 in [(t3 - 1) % n, (t3 + 1) % n]:
gain4 = gain3 + dist(t3, t4)
t3t4gain4.append((t3, t4, gain4))
if not t3t4gain4:
continue
t3t4gain4 = np.array(t3t4gain4, dtype=dtype)
for t3, t4, gain4 in np.sort(t3t4gain4, order='gain')[::-1]:
if gain4 - dist(t4, t1) > 1e-9:
if feasible([t1, t2, t3, t4]):
move()
return True
t5t6gain6 = []
for t5 in tour_index[candidate_set[tour[t4]]]:
if t5 in [(t4 - 1) % n, (t4 + 1) % n]:
continue
gain5 = gain4 - dist(t4, t5)
if gain5 < 0:
continue
for t6 in [(t5 - 1) % n, (t5 + 1) % n]:
gain6 = gain5 + dist(t5, t6)
t5t6gain6.append((t5, t6, gain6))
if not t5t6gain6:
continue
t5t6gain6 = np.array(t5t6gain6, dtype=dtype)
for t5, t6, gain6 in np.sort(t5t6gain6, order='gain')[::-1]:
if gain6 - dist(t6, t1) > 1e-9:
if feasible([t1, t2, t3, t4, t5, t6]):
move()
return True
t7t8gain8 = []
for t7 in tour_index[candidate_set[tour[t6]]]:
if t7 in [(t6 - 1) % n, (t6 + 1) % n]:
continue
gain7 = gain6 - dist(t6, t7)
if gain7 < 0:
continue
for t8 in [(t7 - 1) % n, (t7 + 1) % n]:
gain8 = gain7 + dist(t7, t8)
t7t8gain8.append((t7, t8, gain8))
if not t7t8gain8:
continue
t7t8gain8 = np.array(t7t8gain8, dtype=dtype)
for t7, t8, gain8 in np.sort(t7t8gain8, order='gain')[::-1]:
if gain8 - dist(t8, t1) > 1e-9:
if feasible([t1, t2, t3, t4, t5, t6, t7, t8]):
move()
return True
t9t10gain10 = []
for t9 in tour_index[candidate_set[tour[t8]]]:
if t9 in [(t8 - 1) % n, (t8 + 1) % n]:
continue
gain9 = gain8 - dist(t8, t9)
if gain9 < 0:
continue
for t10 in [(t9 - 1) % n, (t9 + 1) % n]:
gain10 = gain9 + dist(t9, t10)
t9t10gain10.append((t9, t10, gain10))
if not t9t10gain10:
continue
t9t10gain10 = np.array(t9t10gain10, dtype=dtype)
for t9, t10, gain10 in np.sort(t9t10gain10, order='gain')[::-1]:
if gain10 - dist(t10, t1) > 1e-9:
if feasible([t1, t2, t3, t4, t5, t6, t7, t8, t9, t10]):
move()
return True
return False
while kopt() or double_bridge():
pass
return tour
以上が k の最大値 K = 5 での 動的 k-opt の実装になります。
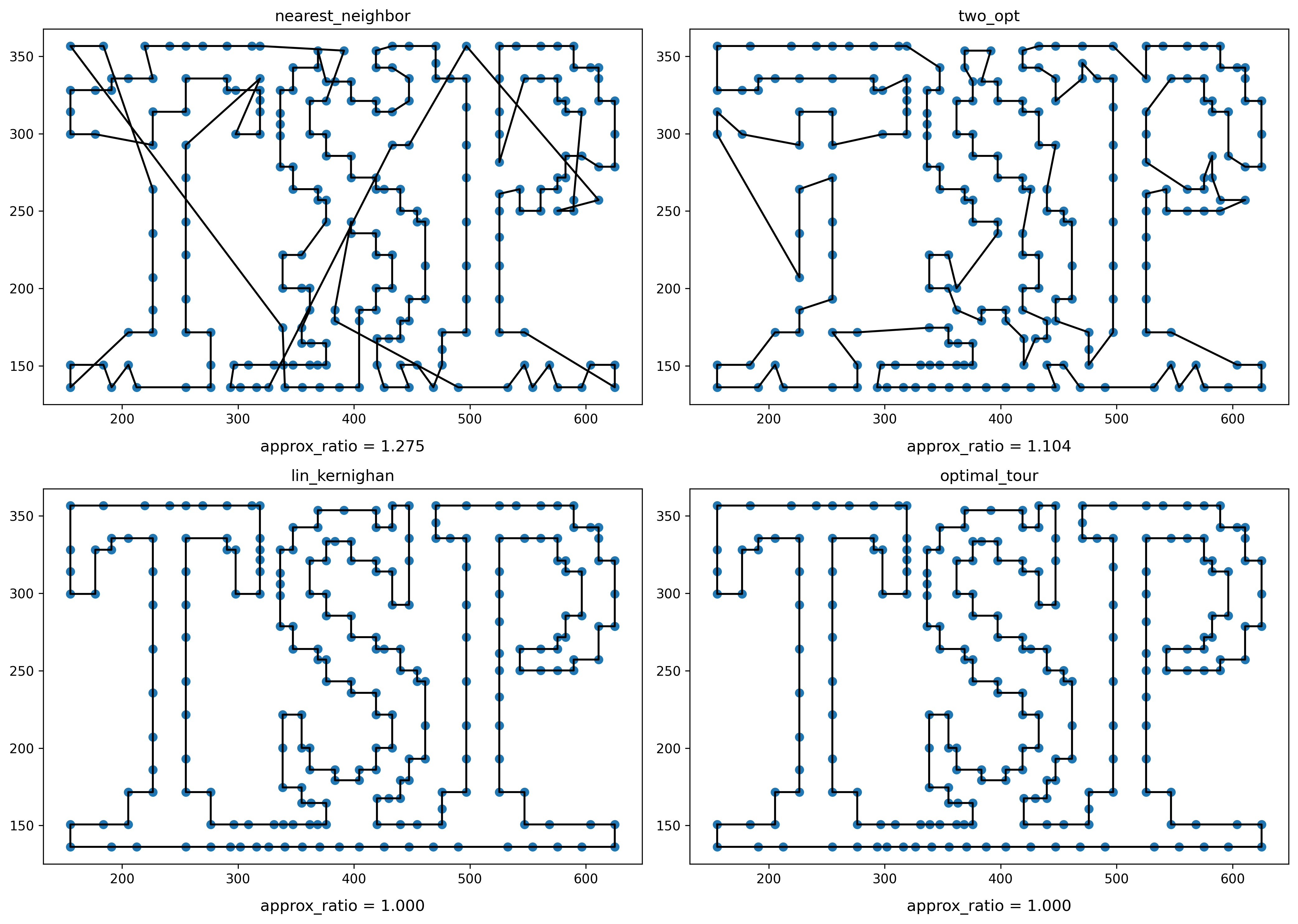
最適解が視覚的に分かりやすい tsp225 で結果を見てみましょう。
target_file = 'tsp225'
read_points()
read_optimal_tour()
plt.figure(figsize=(7 * 2, 5 * 2), dpi=300)
seed = 0
tour = nearest_neighbor()
plt.subplot(2, 2, 1)
plt.title('nearest_neighbor')
plot_points()
plot_tour()
plot_approx_ratio()
nn_tour = tour.copy()
tour = two_opt()
plt.subplot(2, 2, 2)
plt.title('two_opt')
plot_points()
plot_tour()
plot_approx_ratio()
candidate_set = five_nearest_neighbors_graph()
tour = nn_tour.copy()
tour = lin_kernighan()
plt.subplot(2, 2, 3)
plt.title('lin_kernighan')
plot_points()
plot_tour()
plot_approx_ratio()
tour = optimal_tour
plt.subplot(2, 2, 4)
plt.title('optimal_tour')
plot_points()
plot_tour()
plot_approx_ratio()
plt.tight_layout()
plt.show()
seed = 0 で嬉しいことに最適解が得られました。
ちなみに繰り返し部分に再帰を用いればずっと短く書けますし、K の値も動的にできます。若干読みづらくはなりますが、処理を共通化しただけで K = 5 での動作は変わりません。
def lin_kernighan(K=5):
rng = np.random.default_rng(seed)
dtype = [('ta', np.int32), ('tb', np.int32), ('gain', np.float64)]
def kopt():
tour_index = np.argsort(tour)
t = np.empty(2 * K, np.int32)
def rec(k, gain0):
t1 = t[0]
t2 = t[2 * k + 1]
t3t4gain2 = []
for t3 in tour_index[candidate_set[tour[t2]]]:
if t3 in [(t2 - 1) % n, (t2 + 1) % n]:
continue
gain1 = gain0 - dist(t2, t3)
if gain1 < 0:
continue
for t4 in [(t3 - 1) % n, (t3 + 1) % n]:
gain2 = gain1 + dist(t3, t4)
t3t4gain2.append((t3, t4, gain2))
if not t3t4gain2:
return False
t3t4gain2 = np.array(t3t4gain2, dtype=dtype)
for t3, t4, gain2 in np.sort(t3t4gain2, order='gain')[::-1]:
t[2 * k + 2 : 2 * k + 4] = [t3, t4]
if gain2 - dist(t4, t1) > 1e-9:
if feasible(t[:2 * k + 4]):
move()
return True
if k + 2 < K and rec(k + 1, gain2):
return True
return False
for t1 in rng.permutation(n):
for t2 in [(t1 + 1) % n, (t1 - 1) % n]:
t[:2] = [t1, t2]
if rec(0, dist(t1, t2)):
return True
return False
while kopt() or double_bridge():
pass
return tour
気になる方は K の値を変えて実行時間や近似率の変化を確認してみてください。
Lin-Kernighan-Helsgaun Algorithm
『An Effective Implementation of the Lin-Kernighan Traveling Salesman Heuristic』(K. Helsgaun, 2000),
『An Effective Implementation of K-opt Moves for the Lin-Kernighan TSP Heuristic』(K. Helsgaun, 2006),
『General k-opt submoves for the Lin–Kernighan TSP heuristic』(K. Helsgaun, 2009)
による解法です。
これまでの Lin-Kernighan アルゴリズムを踏襲しつつ、追加辺の候補集合の改善やこれまで double-bridge に頼りきりだった non-sequential move を拡充・統合した General k-opt の採用、そしてパーティション分割による高速化と盛りだくさんな内容となっています。
まずは追加辺の候補集合について見ていきましょう。
α-nearest Candidate Set
Lin, Kernighan は候補集合に "five nearest neighbors" を用いました。
しかし追加辺の候補集合が最適解の辺を取りこぼすのは近似率を悪化させる重大なリスクとなります。
上図は pr144 についての結果です。最適解の辺が大部分にわたって欠けてしまっていますね。
もちろん近隣点の数を 5 から増やせばこうした事態は避けやすくなりますが、実行時間への影響が大きいため現実的ではないでしょう。
そこで Helsgaun は "five $\alpha$-nearest neighbors" を用いることにしました。簡単に言えば、より優れた距離 $\alpha$ を定義して近隣 5 点を選ぶ作戦に出たのです。
$\alpha$ を得る手法として Helsgaun が着目したのは全域木から作られる 1-木 でした。
1-木は特殊ノード $1$ を除いた全域木に後から $1$ を接続することで閉路を作り出したものをいいます。閉路を含むため正確には木ではありません。
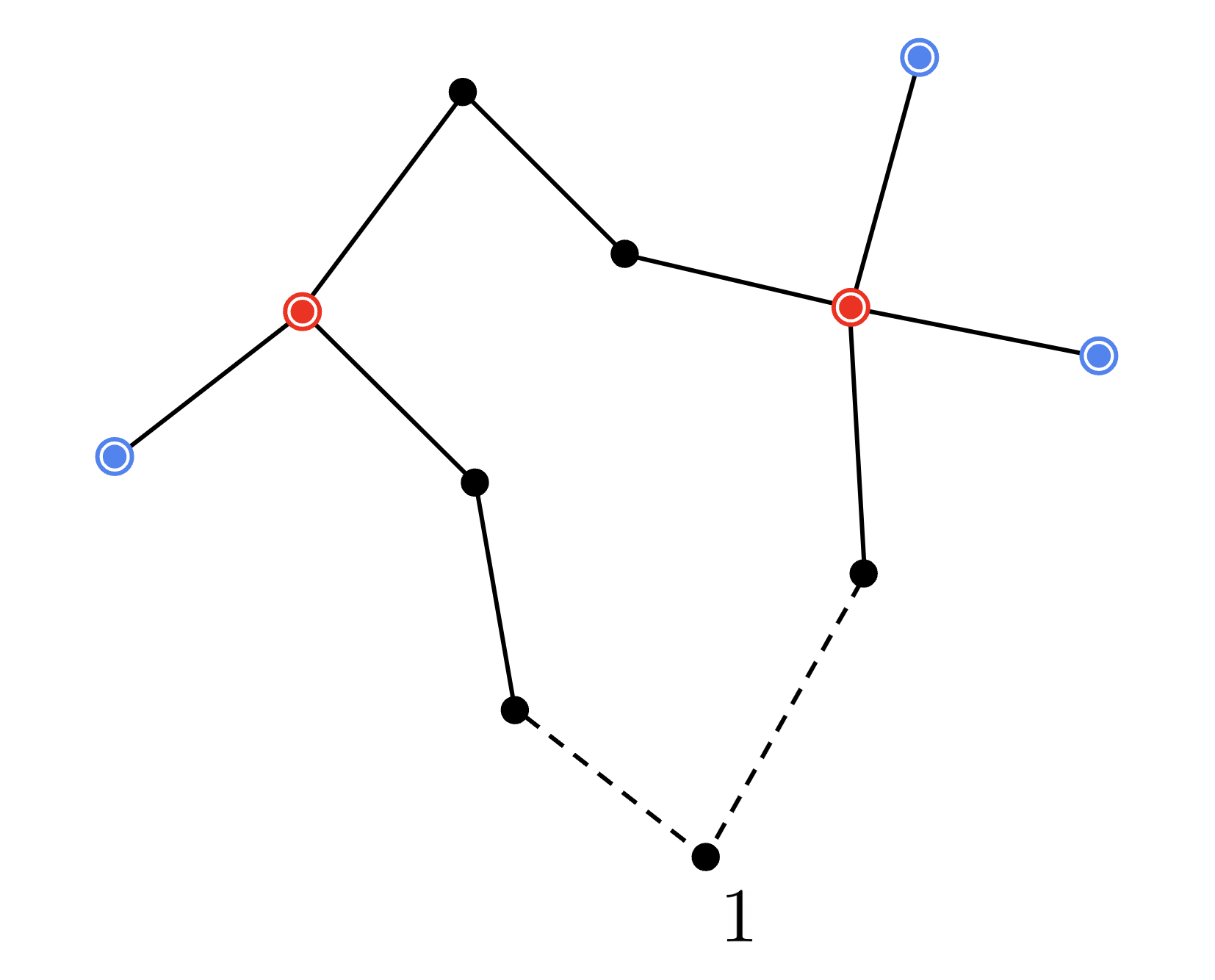
上図は次数が 1 の頂点を青、次数が 3 以上の頂点を赤で示した 最小 1-木 の例になります。
仮に 最小 1-木 の全ての頂点が次数 2 だった場合、それはコスト最小の巡回路、即ち巡回セールスマン問題の最適解に一致します。最小 1-木 は最適解の優れた近似になっており、実に最適解の 70~80% の辺を含むことが分かっています。
Helsgaun はこれを受けて 2点 $i, j$ の距離 $\alpha(i, j)$ を $($辺 $[i,j]$ を必ず含むもとでの 最小 1-木 のコスト$)$ $-$ $($最小 1-木 のコスト$)$ で定義しました。
$\alpha(i, j)$ は常に 0 以上であり、$i, j$ について以下の 3 通りで場合分けすることができます。
- $\ $辺 $[i,j]$ が 最小 1-木 に含まれる
- $\ $$i = 1$ または $j = 1$
- $\ $その他
1 の場合は明らかに $\alpha(i, j) = 0$ ですね。
2 の場合は 辺 $[i,j]$ が特殊ノード $1$ に接続しますから、$\alpha(i,j) = {}$最小 1-木 で $1$ に接続する2辺のうち長い方を削除し 辺 $[i,j]$ を追加した際の増加コスト と分かります。
問題はその他の 3 の場合です。
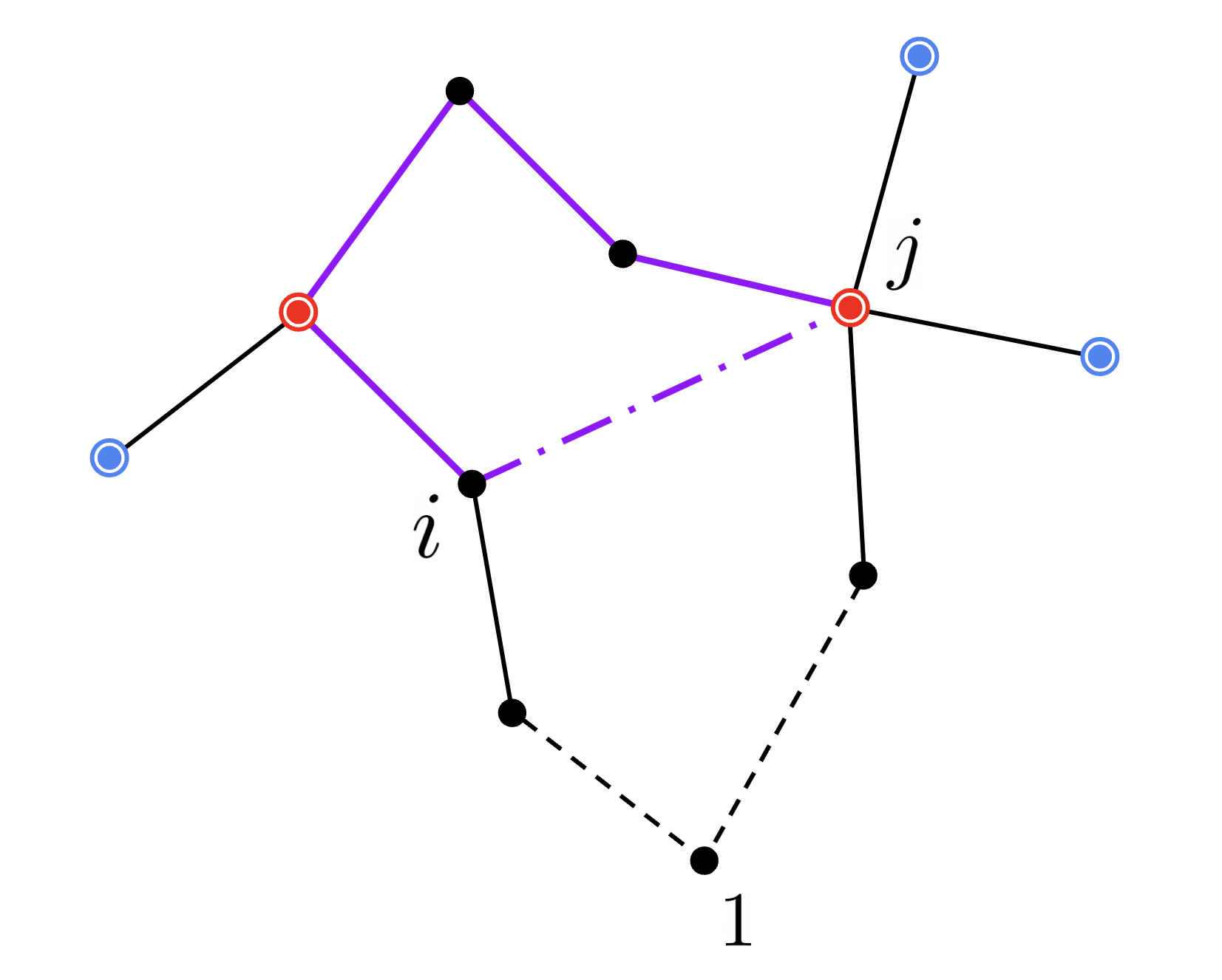
辺 $[i,j]$ を追加すると上図紫色で示した部分に新たな閉路ができてしまいます。したがって $\alpha(i,j) = {}$この閉路で最長の辺を削除し 辺 $[i,j]$ を追加した際の増加コスト と分かります。
ここで木における $j$ の親 $k := \mathrm{parent}[j]$ を考えてみましょう。

辺 $[i,j]$ が作り出した閉路を解消するために削除する最長の辺は、辺 $[i,k]$ が作るオレンジ色で示した閉路の辺と 辺 $[k,j]$ のうち最長の辺になっています。
したがって辺 $[i,j]$ に対し辺長を $c(i,j)$, 閉路の削除辺長を $\beta(i,j)$ と置くと $\beta(i,j) = \max (\beta(i, k), c(k,j))$ で $\beta$ が再帰的に求まるわけです。
しかしこのまま $\beta(i,j)$ を計算すると空間計算量が $O(n^2)$ になってしまうので、追加辺 $[i,j]$ の始点 $i$ を固定して $\beta(j)$ を求めることにします。
def five_alpha_nearest_neighbors_graph():
tri = Delaunay(points[:-1]).simplices
delaunay_edges = np.dstack((tri, np.roll(tri, -1, axis=1))).reshape(-1, 2)
delaunay_graph = nx.from_edgelist(delaunay_edges)
for a, b in delaunay_graph.edges:
delaunay_graph.edges[a, b]['weight'] = point_dist(points[a], points[b])
one_tree = nx.minimum_spanning_tree(delaunay_graph)
a, b = np.argpartition(np.linalg.norm(points[:-1] - points[-1], axis=1), 1)[:2]
one_tree.add_edge(n - 1, a)
one_tree.add_edge(n - 1, b)
dfs_order = np.array(list(nx.dfs_preorder_nodes(one_tree, source=0)))
dfs_edges = np.array(list(nx.dfs_edges(one_tree, source=0)))
parent = np.r_[[0], dfs_edges[np.argsort(dfs_edges[:, 1])][:, 0]]
return _five_alpha_nearest_neighbors_graph(n, points, dfs_order, parent)
@njit(cache=True)
def _five_alpha_nearest_neighbors_graph(n, points, dfs_order, parent):
alpha = np.empty(n)
beta = np.empty(n)
beta_startpoint = -np.ones(n, dtype=np.int64)
five_nearest_neighbors = np.empty((n, 5), dtype=np.int64)
ck = np.sqrt(np.sum((points - points[parent]) ** 2, axis=1))
for i in dfs_order:
beta[i] = -np.inf
j = i
while j != 0:
k = parent[j]
beta[k] = max(beta[j], ck[j])
beta_startpoint[k] = i
j = k
ci = np.sqrt(np.sum((points - points[i]) ** 2, axis=1))
for j in dfs_order:
if j != i and beta_startpoint[j] != i:
k = parent[j]
beta[j] = max(beta[k], ck[j])
alpha[j] = ci[j] - beta[j]
top_five = np.argpartition(alpha, 4)[:5]
five_nearest_neighbors[i] = top_five[np.argsort(alpha[top_five])]
return five_nearest_neighbors
まず特殊ノード points[-1] を除いた points[:-1] から 最小全域木 (minimum spanning tree, MST) を構築し、特殊ノードとそれにもっとも近い2点を隣接させて 最小 1-木 を作ります。
(ここでは最小全域木を完全に含むことが知られているドロネー図(ドロネー三角形分割)からの構築を行いました)
以下、木の根(root)は 0 とします。
dfs_order は深さ優先探索(dfs)の行きがけ順を表します。幅優先探索でも構いません。この順序は dfs_order[i] == parent[dfs_order[j]] のとき必ず dfs_order[i] < dfs_order[j] を満たします。即ち親が先に現れます。
parent は深さ優先探索で行きがけ順に得られるエッジリストをソートすれば簡単に手に入りますね。もちろん幅優先探索でも構いません。
@njit による高速化のためだけに、ここで関数を切り離しました。あとは $\beta$ を埋めて $\alpha(i,j) = c(i,j) - \beta(j)$ がもっとも小さくなるような 5 つの $j$ を求めるだけです。
先の図解により木の親から子へと $\beta$ が次々計算できることが分かっているため、根 0 に対する $\beta(0)$ を求められれば dfs_order にしたがって任意の $\beta(j)$ が計算できるようになります。
ここで追加辺 $[i,\mathrm{parent}[i]]$ は明らかに 1-木 に含まれるので、これにより $$\beta(\mathrm{parent}[i]) = c(i, \mathrm{parent}[i])$$ が得られます。追加辺 $[i,\mathrm{parent[parent}[i]]]$ については閉路で最長の辺を削除することを考えて$$\beta(\mathrm{parent[parent}[i]]) = \max(\beta(\mathrm{parent}[i]), c(\mathrm{parent}[i], \mathrm{parent[parent}[i]]))$$ が得られますね。これを $\beta(0)$ までループさせれば良さそうです。ここで求めた $\beta(j)$ の始点 $i$ は beta_startpoint[j] に保存しておき、その後 dfs_order にしたがって更新する際に求値済みの $\beta(j)$ が上書きされないようにしています。
five = np.argpartition(alpha, 4)[:5] は alpha 中でもっとも小さい 5 つの要素のインデックスを未ソートで得るものです。これは $O(n)$ で求まるため np.argsort(alpha)[:5] などとするより実行時間の短縮に役立ちます。あとは five を alpha に沿ってソートし five_nearest_neighbors[i] に記録すれば完成です。
早速 pr144 で試してみましょう。
target_file = 'pr144'
read_points()
read_optimal_tour()
plt.figure(figsize=(7 * 2, 5 * 2), dpi=300)
candidate_set = five_nearest_neighbors_graph()
plt.subplot(2, 2, 1)
plt.title('five_nearest_neighbors')
plot_points()
plot_candidate_set_graph()
candidate_set = five_alpha_nearest_neighbors_graph()
plt.subplot(2, 2, 2)
plt.title('five_alpha_nearest_neighbors')
plot_points()
plot_candidate_set_graph()
tour = optimal_tour
plt.subplot(2, 2, 3)
plt.title('optimal_tour')
plot_points()
plot_tour()
plt.tight_layout()
plt.show()
$\alpha$ を用いたことで最適解により一層近づいたことが分かります。
improved α
すでに良質な候補集合が得られていますが、Helsgaun は 1-木 にもう一手間加えることでさらに最適解に近い候補集合が得られることを示しました。
すべての頂点の次数が 2 であるような 最小 1-木 は巡回セールスマン問題の最適解に一致するのでした。であれば、上手いこと 次数 3 以上の頂点に接続する辺を減らして 次数 1 の頂点に接続する辺を増やせば より優れた 最小 1-木 が得られるはずです。
これを達成するため Helsgaun は各頂点の次数が 2 に近づくよう 各頂点 $i$ に対して接続ペナルティ $\pi_i$ を新たに適用し、辺 $[i,j]$ のコストを $c(i,j) + \pi_i + \pi_j$ に置き直した上で 最小 1-木 を求めることにしました。
この $\pi$ の値を各頂点の次数 $d$ について $d - 2$ の方向へ移動させることで、次数が 1 の頂点への接続コストは減少し、次数が 3 以上の頂点への接続コストは増加することが分かります。
TSP 解では各頂点に必ず 2 本の辺が接続するため、どのような解であってもこの追加コストの合計は $2\sum_i\pi_i$ に固定されます。したがって $\pi$ は 最小 1-木 にこそ影響しますが、巡回セールスマン問題の最適解には一切影響しません。
この新しいコスト $c(i,j) + \pi_i + \pi_j$ を用いて $\alpha$ を求めることで、最適解の 2 辺がより小さい $\alpha$ 値をもつ傾向にあることが実験的に示されたのです。
def five_improved_alpha_nearest_neighbors_graph():
rng = np.random.default_rng(seed)
tri = Delaunay(points[:-1]).simplices
delaunay_edges = np.dstack((tri, np.roll(tri, -1, axis=1))).reshape(-1, 2)
delaunay_graph = nx.from_edgelist(delaunay_edges)
for a, b in delaunay_graph.edges:
delaunay_graph.edges[a, b]['weight'] = point_dist(points[a], points[b])
one_tree = nx.minimum_spanning_tree(delaunay_graph)
a, b = np.argpartition(np.linalg.norm(points[:-1] - points[-1], axis=1), 1)[:2]
one_tree.add_edge(n - 1, a)
one_tree.add_edge(n - 1, b)
dfs_order = np.array(list(nx.dfs_preorder_nodes(one_tree, source=0)))
dfs_edges = np.array(list(nx.dfs_edges(one_tree, source=0)))
parent = np.r_[[-1], dfs_edges[np.argsort(dfs_edges[:, 1])][:, 0]]
m = 10
pi = np.zeros(n)
m_nearest_neighbors = _m_alpha_pi_nearest(m, n, points, dfs_order, parent, pi)
edges = np.c_[np.arange(n).repeat(m), m_nearest_neighbors.ravel()]
weights = np.linalg.norm(points[edges[:, 0]] - points[edges[:, 1]], axis=1)
G = nx.from_edgelist(edges)
degree = np.array(sorted(one_tree.degree()))[:, 1]
v = degree - 2
best_w = -np.inf
period = 64
t = 1
while period > 0:
improved = False
for p in range(period):
prev_v = v
v = degree - 2
pi += t * (0.7 * v + 0.3 * prev_v)
for (a, b), weight in zip(edges, weights):
G.edges[a, b]['weight'] = weight + pi[a] + pi[b]
special_node = rng.choice(np.arange(n)[degree == 1])
special_edges = [(a, b, d['weight']) for a, b, d in G.edges(special_node, data=True)]
G.remove_node(special_node)
one_tree = nx.minimum_spanning_tree(G)
one_tree.add_weighted_edges_from(sorted(special_edges, key=lambda e: e[2])[:2])
degree = np.array(sorted(one_tree.degree()))[:, 1]
G.add_weighted_edges_from(special_edges)
w = one_tree.size(weight='weight') - 2 * pi.sum()
if w > best_w:
improved = True
best_w = w
best_pi = pi.copy()
if not improved:
period //= 2
t /= 2
return _m_alpha_pi_nearest(5, n, points, dfs_order, parent, best_pi)
@njit(cache=True)
def _m_alpha_pi_nearest(m, n, points, dfs_order, parent, pi):
alpha = np.empty(n)
beta = np.empty(n)
beta_startpoint = -np.ones(n, dtype=np.int64)
m_nearest_neighbors = np.empty((n, m), dtype=np.int64)
ck = np.sqrt(np.sum((points - points[parent]) ** 2, axis=1))
for i in dfs_order:
beta[i] = -np.inf
j = i
while j != 0:
k = parent[j]
beta[k] = max(beta[j], ck[j] + pi[j] + pi[k])
beta_startpoint[k] = i
j = k
ci = np.sqrt(np.sum((points - points[i]) ** 2, axis=1))
for j in dfs_order:
if j != i and beta_startpoint[j] != i:
k = parent[j]
beta[j] = max(beta[k], ck[j] + pi[j] + pi[k])
alpha[j] = ci[j] + pi[i] + pi[j] - beta[j]
top_m = np.argpartition(alpha, m - 1)[:m]
m_nearest_neighbors[i] = top_m[np.argsort(alpha[top_m])]
return m_nearest_neighbors
$\pi$ の最適化は $\pi$ を $v = d - 2$ の方向に移動させるだけです。それさえ守られていれば、それ以外は自由に設計して構いません。ここでは振動を抑制するため pi += t * (0.7 * v + 0.3 * prev_v) としています。
$w = \left|\mathrm{minimum\ 1\text{-}tree}\right| - 2\sum_i\pi_i$ はなんぞやというと、これは求めた 最小 1-木 が巡回セールスマン問題の最適解に近いほど大きくなるような値になっています。各頂点の次数に制限のない最小 1-木 は、各頂点の次数が 2 に制限されている巡回セールスマン問題の最適解のコストを上回ることがないためです。
したがってこの $w$ の最大化が分かりやすい目標となりますね。
target_file = 'pr144'
read_points()
read_optimal_tour()
plt.figure(figsize=(7 * 2, 5 * 2), dpi=300)
candidate_set = five_alpha_nearest_neighbors_graph()
plt.subplot(2, 2, 1)
plt.title('five_alpha_nearest_neighbors')
plot_points()
plot_candidate_set_graph()
candidate_set = five_improved_alpha_nearest_neighbors_graph()
plt.subplot(2, 2, 2)
plt.title('five_improved_alpha_nearest_neighbors')
plot_points()
plot_candidate_set_graph()
tour = optimal_tour
plt.subplot(2, 2, 3)
plt.title('optimal_tour')
plot_points()
plot_tour()
plt.tight_layout()
plt.show()
上部で欠けていた最適解の辺がカバーされるようになりました。
General k-opt
さて、最後に General k-opt を実装していきましょう。
これまでの Lin-Kernighan アルゴリズムでは non-sequential な改善を double-bridge と呼ばれる non-sequential 4-opt で付加的に実現していました。
これを non-sequential k-opt に拡張し sequential k-opt とも統合させることができれば さらに探索範囲を広げられるはずです。
double-bridge が 実行不可能な 2-opt を利用したことに着目すれば、non-sequential k-opt は実行不可能な k-opt によって巡回路を複数個(最大 k 個)に分割し、得られたそれぞれのサイクルをさらに k-opt でひと繋ぎに縫い合わせることで実現できそうだと気が付きます。
では feasible(t) で実行不可能な $\boldsymbol{t}$ が与えられた時、サイクルのリスト cycles をグローバルに保存するよう変更しましょう。
cycles = None
feasible_key_cache = set()
nonfeasible_cycles_cache = dict()
def feasible_lkh(t):
global cycles
unique_t, compressed_t = np.unique(t, return_inverse=True)
key = compressed_t.tobytes()
if key in feasible_key_cache:
return True
if key in nonfeasible_cycles_cache:
cycle_paths, cycle_directions = nonfeasible_cycles_cache[key]
cycles = [[(unique_t[a], unique_t[b], *d) for (a, b), d in zip(path, direction)] for path, direction in zip(cycle_paths, cycle_directions)]
return False
X = compressed_t.reshape(-1, 2)
Y = np.roll(compressed_t, -1).reshape(-1, 2)
G = nx.cycle_graph(u := unique_t.size, nx.MultiGraph)
G.add_edges_from(Y)
G.remove_edges_from(X)
if nx.is_connected(G):
feasible_key_cache.add(key)
return True
X = nx.from_edgelist(X)
Y = nx.from_edgelist(Y)
cycle_paths = []
cycle_directions = []
for cycle in nx.simple_cycles(G):
init, tail = max(nx.cycle_graph(cycle).edges & Y.edges)
G.remove_edge(tail, init)
cycle_path = []
is_path = True
for a, b in nx.dfs_edges(G, source=init):
if is_path:
if b not in [(a - 1) % u, (a + 1) % u] or (a, b) in X.edges:
cycle_path.append([a, a])
continue
cycle_path.append([a, b])
is_path = not is_path
if is_path:
cycle_path.append([tail, tail])
cycle_paths.append(cycle_path)
cycle_direction = np.sign(np.diff(cycle_path, axis=1))
cycle_direction[np.all(cycle_path == np.array([0, u - 1]), axis=1)] = -1
cycle_direction[np.all(cycle_path == np.array([u - 1, 0]), axis=1)] = 1
cycle_directions.append(cycle_direction)
nonfeasible_cycles_cache[key] = [cycle_paths, cycle_directions]
cycles = [[(unique_t[a], unique_t[b], *d) for (a, b), d in zip(path, direction)] for path, direction in zip(cycle_paths, cycle_directions)]
return False
cycles は個々のサイクルについて route を求めるときと同様にして簡単に求められます。要するにそれぞれのサイクルに対し追加辺 [tail, init] を一つ選んで削除し、init から深さ優先探索順に辺を追加する、これをサイクルの数だけ行えば cycles の完成です。
たとえば実行不可能な 2-opt の例を入力すると次のようなサイクルが返ります。
print(feasible_lkh([1, 2, 3, 4]))
print(cycles)
>> False
>> [[(2, 3, 1)], [(4, 1, 1)]]
ちゃんと下図に一致しています。
このような 5-opt の例でも
print(feasible_lkh([1, 2, 4, 3, 9, 10, 7, 8, 5, 6]))
print(cycles)
>> False
>> [[(8, 9, 1), (3, 2, -1), (4, 5, 1)], [(10, 1, 1), (6, 7, 1)]]
問題なくサイクルを取得できていますね。
得られたサイクルをそれぞれ線形補間しておく関数も定義しておきます。
def interpolated_cycles():
return [np.concatenate([interpolate(a, b, d) for a, b, d in cycle]) for cycle in cycles]
これでようやく Lin-Kernighan-Helsgaun を実装する手立てが整いました。
要点は以下の通りです。
- 基本は Lin-Kernighan と同じ
- ただし追加辺 $[t_4, t_1]$ で閉じた際に
gainが正かつ実行不可能であればサイクルを縫い合わせる k-opt を追加で呼び出す- この k-opt の変数を $\boldsymbol{s} = [s_1, s_2, s_3, s_4, \cdots]$ とする
- ただし追加辺 $[t_4, t_1]$ で閉じた際に
- 縫い合わせはもっとも頂点数の少ない
shortest_cycleからスタートし、このサイクルに別のサイクルを繋ぎ合わせ、サイクルの数を減らしていくことで達成できる - $s_1$ を
shortest_cycleからランダムに選択し、$s_2$ を $s_1 + 1, s_1 - 1$ から選ぶ- $s_3$ を $s_2$ にもっとも近い 5 点から順に選ぶ
- $s_3$ の属するサイクルが $s_1, s_2$ と同じならこの $s_3$ をスキップする
- ここまでの
gainを計算し、負なら この $s_3$ をスキップする- $s_4$ を $s_3 - 1, s_3 + 1$ から選ぶ
- 追加辺 $[s_4, s_1]$ で閉じた際に
gainが正なら$\cdots$- 残りサイクル数が 1 なら解を改善してステップ終了
- そうでなければ
best_closeup_gainを更新する
- $s_5$ を $s_4$ にもっとも近い 5 点から順に選ぶ
- $\cdots$以降 繰り返し
- 追加辺 $[s_4, s_1]$ で閉じた際に
- $s_4$ を $s_3 - 1, s_3 + 1$ から選ぶ
-
best_closeup_gainが正ならこのベストな $\boldsymbol{s}$ について一度縫い合わせを閉じ、残ったサイクルについてさらに縫い合わせを呼び出す- 前提として k-opt では一度に k - 1 個のサイクルを
shortest_cycleに縫い合わせて減らすことができる - そこで、例えばサイクルが 5 つあったとき [5-opt], [4-opt + 2-opt], [3-opt + 3-opt], [3-opt + 2-opt + 2-opt] $\cdots$ など複数回 k-opt を掛け合わせる探索も行われる
- 前提として k-opt では一度に k - 1 個のサイクルを
- 改善に失敗した時点で無限ループを抜けて終了する
def lin_kernighan_helsgaun(K=5):
rng = np.random.default_rng(seed)
def general_kopt():
tour_index = np.argsort(tour)
t = np.empty(2 * K, np.int64)
tour_graph = nx.cycle_graph(n, nx.MultiGraph)
def move():
tour[:] = tour[list(nx.dfs_preorder_nodes(tour_graph))]
def patch_cycles(cycles, init_closeup_gain):
s = np.empty(2 * K, np.int64)
cycle_index = np.empty(n, np.int64)
for i, cycle in enumerate(cycles):
cycle_index[cycle] = i
def patch_cycles_rec(k, l, gain0):
l -= 1
s1 = s[0]
s2 = s[2 * k + 1]
ci = cycle_index[s1]
best_closeup_gain = 0
for s3 in tour_index[candidate_set[tour[s2]]]:
if s3 in [(s2 - 1) % n, (s2 + 1) % n]:
continue
cj = cycle_index[s3]
if ci == cj:
continue
gain1 = gain0 - dist(s2, s3)
if gain1 < 0:
continue
tour_graph.add_edge(s2, s3)
for s4 in [(s3 - 1) % n, (s3 + 1) % n]:
if not tour_graph.has_edge(s3, s4):
continue
tour_graph.remove_edge(s3, s4)
gain2 = gain1 + dist(s3, s4)
s[2 * k + 2 : 2 * k + 4] = [s3, s4]
if (closeup_gain := gain2 - dist(s4, s1)) > 1e-9:
tour_graph.add_edge(s4, s1)
if l == 1:
move()
return True
if closeup_gain > best_closeup_gain:
best_closeup_gain = closeup_gain
best_s3, best_s4 = s3, s4
tour_graph.remove_edge(s4, s1)
if l >= 2 and k + 2 < K:
cycle_index[cycles[cj]] = ci
if patch_cycles_rec(k + 1, l, gain2):
return True
cycle_index[cycles[cj]] = cj
tour_graph.add_edge(s3, s4)
tour_graph.remove_edge(s2, s3)
if best_closeup_gain > 1e-9:
s3, s4 = best_s3, best_s4
tour_graph.add_edge(s2, s3)
tour_graph.remove_edge(s3, s4)
tour_graph.add_edge(s4, s1)
cj = cycle_index[s3]
patched_cycles = [np.concatenate([cycle for cycle in cycles if cycle_index[cycle[0]] in (ci, cj)])]
remain_cycles = [cycle for cycle in cycles if cycle_index[cycle[0]] not in (ci, cj)]
if patch_cycles(patched_cycles + remain_cycles, best_closeup_gain):
return True
tour_graph.remove_edge(s4, s1)
tour_graph.add_edge(s3, s4)
tour_graph.remove_edge(s2, s3)
return False
shortest_cycle = min(cycles, key=len)
for s1 in rng.permutation(shortest_cycle):
for s2 in [(s1 + 1) % n, (s1 - 1) % n]:
if not tour_graph.has_edge(s1, s2):
continue
tour_graph.remove_edge(s1, s2)
s[:2] = [s1, s2]
if patch_cycles_rec(0, len(cycles), init_closeup_gain + dist(s1, s2)):
return True
tour_graph.add_edge(s1, s2)
return False
def general_kopt_rec(k, gain0):
t1 = t[0]
t2 = t[2 * k + 1]
for t3 in tour_index[candidate_set[tour[t2]]]:
if t3 in [(t2 - 1) % n, (t2 + 1) % n]:
continue
gain1 = gain0 - dist(t2, t3)
if gain1 < 0:
continue
tour_graph.add_edge(t2, t3)
for t4 in [(t3 - 1) % n, (t3 + 1) % n]:
if not tour_graph.has_edge(t3, t4):
continue
tour_graph.remove_edge(t3, t4)
gain2 = gain1 + dist(t3, t4)
t[2 * k + 2 : 2 * k + 4] = [t3, t4]
if t1 not in [t3, t4] and (closeup_gain := gain2 - dist(t4, t1)) > 1e-9:
tour_graph.add_edge(t4, t1)
if feasible_lkh(t[:2 * k + 4]):
move()
return True
if patch_cycles(interpolated_cycles(), closeup_gain):
return True
tour_graph.remove_edge(t4, t1)
if k + 2 < K and general_kopt_rec(k + 1, gain2):
return True
tour_graph.add_edge(t3, t4)
tour_graph.remove_edge(t2, t3)
return False
for t1 in rng.permutation(n):
for t2 in [(t1 + 1) % n, (t1 - 1) % n]:
tour_graph.remove_edge(t1, t2)
t[:2] = [t1, t2]
if general_kopt_rec(0, dist(t1, t2)):
return True
tour_graph.add_edge(t1, t2)
return False
while general_kopt():
pass
return tour
pr144 で結果を確認してみましょう。
target_file = 'pr144'
read_points()
read_optimal_tour()
plt.figure(figsize=(7 * 2, 5 * 2), dpi=300)
seed = 0
tour = nearest_neighbor()
plt.subplot(2, 2, 1)
plt.title('nearest_neighbor')
plot_points()
plot_tour()
plot_approx_ratio()
nn_tour = tour.copy()
candidate_set = five_nearest_neighbors_graph()
tour = lin_kernighan()
plt.subplot(2, 2, 2)
plt.title('lin_kernighan')
plot_points()
plot_tour()
plot_approx_ratio()
candidate_set = five_improved_alpha_nearest_neighbors_graph()
tour = nn_tour.copy()
tour = lin_kernighan_helsgaun()
plt.subplot(2, 2, 3)
plt.title('lin_kernighan_helsgaun')
plot_points()
plot_tour()
plot_approx_ratio()
tour = optimal_tour
plt.subplot(2, 2, 4)
plt.title('optimal_tour')
plot_points()
plot_tour()
plot_approx_ratio()
plt.tight_layout()
plt.show()
Lin-Kernighan アルゴリズムに比べ大幅に近似率が向上し、無事最適解が得られました。
Partitioning
パーティション分割は $n \ge 100{,}000$ のような超大規模問題に対する実行時間削減のための手法として盛り込まれた内容です。正確な実装は分かりませんが、問題をいくつかの部分問題に分割して解くためさまざまなパーティションを適用しているようです。
筆者は詳しくないため、以下の詳細は元論文を参照してください。
- Tour segment partitioning
- Karp partitioning
- Delaunay partitioning
- K-means partitioning
- Sierpinski partitioning
- Rohe partitioning
partitioning の実装は「異なるパーティションにまたがって辺を追加・削除してはいけない」という制約を付与するだけになります。
partition_index = np.empty(n, np.int64)
for i, partition in enumerate(partitions):
partition_index[partition] = i
そのためこのような partition_index を用意して、追加辺・削除辺の端点 [a, b] が同じパーティションに属すように partition_index[a] == partition_index[b] で制限すればいいわけです。
ただ残念なことに超大規模問題を解くには Python がまず遅すぎるため、やるからには C/C++ などで実装することをおすすめします。
まとめ
TSP 解法として一般的な 最近傍法 や 2-opt を出発点に、非常に強力な Lin-Kernighan, Lin-Kernighan-Helsgaun アルゴリズムの実装まで紹介させていただきました。
近年では Lin-Kernighan-Helsgaun に 深層学習(graph neural network, GNN)を組み合わせることで、より高速かつ優れた近似率を達成する研究が目立っています。
本記事が TSP に興味を持っていただけた方の一助となれば幸いです。