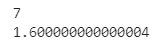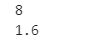「異常検知と変化検知」は異常検知の本です。アルゴリズム部分をpythonで実装していきたいと思います。たくさんの方が同じ内容をより良い記事でとして投稿しています。
個人的な勉強のメモ書きとなります。
コードがかなり汚いです。申し訳ありません。
まとめることが目的ではないので本文について参考書とほぼ同じ表現となっています。問題があればお教えください。
興味を持ったり、導出や詳細などを知りたい方は「異常検知と変化検知」を読んでいただければと思います。
参考
前回
単純ベイズ法による異常検知
近傍法による異常検知
k近傍法:経験分布に基づく異常判定
ラベルなしデータに対するk近傍法
$M$次元ベクトル$\boldsymbol{x}$が$N$個観測されているとする。
$$
D={\boldsymbol{x}^{(1)},\boldsymbol{x}^{(2)},\cdots,\boldsymbol{x}^{(N)}}
$$
$\boldsymbol{x}'$を中心とした半径$\epsilon$の$M$次元旧内部の領域を$V_M(\epsilon,\boldsymbol{x}')$、その体積は$|V_M(\epsilon,\boldsymbol{x}')|$と表す。
任意の位置$\boldsymbol{x}'$での確率密度$p(\boldsymbol{x}')$は、
$$
p(\boldsymbol{x}')\approx\frac{k}{N|V_M(\epsilon,\boldsymbol{x}')|}
$$
となる。
$k$は領域$V_M(\epsilon,\boldsymbol{x}')$に含まれる$D$の要素の数である。
$M$次元空間における球の体積$V_M(\epsilon,\boldsymbol{x}')$は、半径$\epsilon$の$M$乗に比例するから異常度は、
$$
a(\boldsymbol{x}')=-\ln{p(\boldsymbol{x}'})=-\ln{k}+M\ln{\epsilon}+(定数)
$$
となる。
$\epsilon$を固定すれば$k$が小さい方が高い異常度を与え、$k$を固定すれば$\epsilon$が大きい方が高い異常度を与える。
近傍標本数$k$を定数として与えて異常判定を行う方法をk近傍法もしくはk最近傍法と呼ぶ。
逆に、近傍半径$\epsilon$を定数として与えるやり方を $\epsilon$近傍法 と呼ぶ。
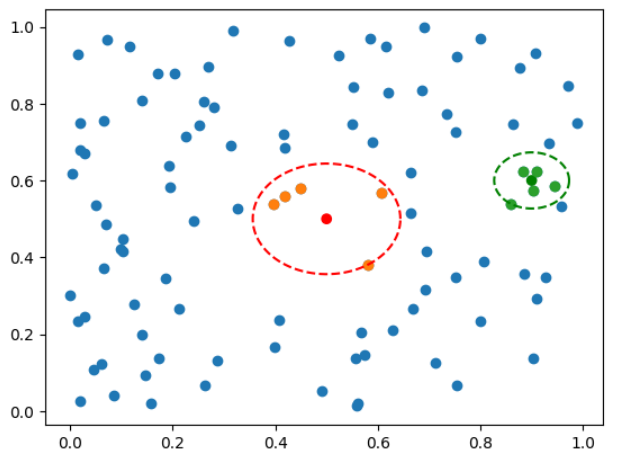
近傍点の例を示す。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)
def make_circle(x, y, r, theta):
"""円の描画用
"""
return np.concatenate([[x + r * np.cos(theta)], [y + r * np.sin(theta)]], axis=0).T
def find_near_k(x1, x2, k):
"""k近傍点の座標と距離
"""
dist = np.sqrt(np.sum((x1- x2.reshape(len(x2),1,2))**2, axis=2))
neark = np.array([x1[np.argsort(dist[i])[:k],:] for i in range(len(x2))])
eps = np.array([np.max(dist.T[np.argsort(dist[i])[:k],i]) for i in range(len(x2))])
return neark, eps
def find_near_eps(x1, x2, eps):
"""epsilon近傍点の数(k)
"""
dist = np.sqrt(np.sum((x1- x2.reshape(len(x2),1,2))**2, axis=2))
k = np.sum(dist<eps, axis=1)
return k
# 訓練用データ
N = 100
x1 = np.random.rand(N, 2)
# テストデータ
x2 = np.array([[0.5, 0.5],
[0.9, 0.6]])
# 各点の近傍点情報を取得
neark, epsk = find_near_k(x1, x2=x2, k=5)
near_eps = find_near_eps(x1, x2, eps=0.1)
# 描画用
theta = np.linspace(0, 2*np.pi, N)
plt.scatter(x1[:,0], x1[:,1]);
plt.scatter(x2[:,0], x2[:,1], color=['red', 'green']);
c1 = make_circle(x2[0,0], x2[0,1], r=epsk[0], theta=theta)
c2 = make_circle(x2[1,0], x2[1,1], r=epsk[1], theta=theta)
plt.scatter(neark[0,:,0], neark[0,:,1]);
plt.scatter(neark[1,:,0], neark[1,:,1]);
plt.plot(c1[:,0], c1[:,1], '--', color='red');
plt.plot(c2[:,0], c2[:,1], '--', color='green');
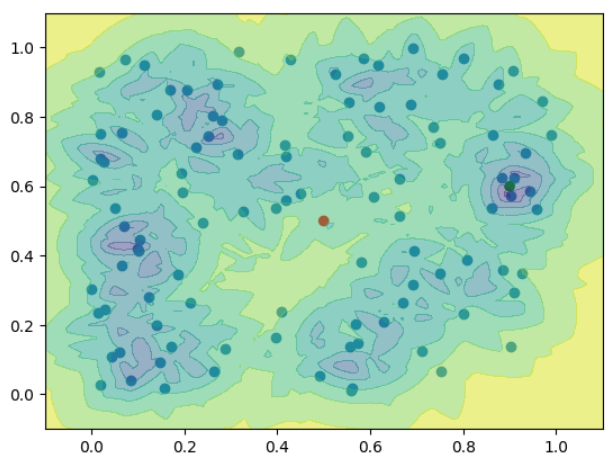
k$近傍法による異常度の分布を示す。
def knn_anomaly(k,N,eps):
return -np.log1p(k/(N*4/3*np.pi*eps**3))
x = np.arange(-0.1,1.1,0.01)
y = np.arange(-0.1,1.1,0.01)
xx, yy = np.meshgrid(x, y)
XY = np.array([xx.ravel(), yy.ravel()]).T
# 近傍点の情報を計算
neark, epsk = find_near_k(x1, x2=XY, k=5)
near_k = find_near_eps(x1, XY, eps=0.1)
# k近傍法
plt.scatter(x1[:,0], x1[:,1]);
plt.scatter(x2[:,0], x2[:,1], color=['red', 'green']);
plt.contourf(xx,yy,knn_anomaly(5, N, epsk).reshape(121,121), alpha=.5)
$\epsilon$近傍法による異常度の分布を示す。
# ε近傍法
plt.scatter(x1[:,0], x1[:,1]);
plt.scatter(x2[:,0], x2[:,1], color=['red', 'green']);
plt.contourf(xx,yy,knn_anomaly(near_k, N, 0.1).reshape(121,121), alpha=.5)
ラベル付きデータに対するk近傍法
$M$次元空間で異常標本と正常標本の双方が明示的に与えられている場合を考える。
ある$\boldsymbol{x}'$に対する異常度を計算するには、あらかじめ与えられた近傍数$k$の数だけ近傍標本を選び、ラベルを確認する。
異常ラベルの付いた近傍標本の数を$N^1(\boldsymbol{x}')$とし、正常ラベルの付いた近傍標本の数を$N^0(\boldsymbol{x}')$とすれば明らかに、
$$
p(y=1|\boldsymbol{x}',D)=\frac{N^1(\boldsymbol{x}')}{k}\
p(y=0|\boldsymbol{x}',D)=\frac{N^0(\boldsymbol{x}')}{k}
$$
が成り立つ。
これにベイズの定理を適用して$\boldsymbol{x}'$と$y$の立場を入れ替えると、異常度は、
$$
a(\boldsymbol{x}')=\ln{\frac{p(\boldsymbol{x}'|y=1,D)}{p(\boldsymbol{x}'|y=0,D)}}=\ln{\frac{\pi^0N^1(\boldsymbol{x}')}{\pi^1N^0(\boldsymbol{x}')}}
$$
のように定義できる。
ただし、$\pi^1$は全標本に対する異常標本の割合、$\pi^0$は全標本に対する異常標本の割合である。
近傍法による異常検知のアルゴリズムを示す。
- 訓練時 探索する$k$と$a_{th}$の候補を挙げておく
距離の定義を決める
それぞれの$(k,a_{th})$について以下を行い、最大のF値を与えるパラメータ$(k^,a^_{th})$を選択する
- $D$の中から標本$\boldsymbol{x}^{(n)}$を選ぶ$(n=1,\cdots,N)$
- 残りの$N-1$個の標本の中から、$\boldsymbol{x}^{(n)}$に最も近い標本を$k$個選ぶ
- $a(\boldsymbol{x}^{(n)})>a_{th}$なら$\boldsymbol{x}^{(n)}$を異常と判定する
- $N$個の標本すべてに判定結果が出そろったら、正常標本精度と異常標本精度を計算し、F値を求める
それを$(k,a_{th})$の評価値とする
- 運用時
- 新たな観測値$\boldsymbol{x}'$に対して、最近傍$k^*$個を$D$から選ぶ
- $a(\boldsymbol{x}'^{(n)})>a^*_{th}$なら$\boldsymbol{x}'$を異常と判定する
今回は、距離尺度としてユークリッド距離を使用する。
def near_k_id(x1, x2, A, k):
"""k近傍点のid
"""
dist=((x1- x2.reshape(len(x2),1,2))@A).reshape(len(x2),len(x1),1,2)@(x1- x2.reshape(len(x2),1,2)).reshape(len(x2),len(x1),2,1)
dist = dist[:,:,0,0]
neark_ids = np.argsort(dist, axis=1)[:,1:k+1]
return neark_ids
def calc_a(y, ath, ids, eps = 1e-3):
"""全標本に対する正常標本・異常標本の割合
"""
pi0 = np.sum(y==0)/len(y)
pi1 = np.sum(y==1)/len(y)
N0 = np.sum(y[ids]==0, axis=1)
N1 = np.sum(y[ids]==1, axis=1)
# 異常度
a = np.log((pi0*N1+eps)/(pi1*N0+eps))
y_pred = (a>ath).astype(int)
return y_pred
def calc_TPTF(A, x, y, k, ath):
"""正常標本精度や異常標本精度、F値などの計算
"""
y_pred = np.zeros(len(x3))
# 1対N-1でラベルの予測
ids = near_k_id(x, x, A, k=k)
y_pred = calc_a(y, ath, ids)
# 正常標本精度と異常標本精とF値
TP = np.sum((y_pred==1)*y) / np.sum(y==1)
TF = np.sum((y_pred==0)*(1-y)) / np.sum(y==0)
F = 2*TP*TF/(TP+TF)
return TP, TF, F, y_pred
# ラベル付きデータの作成
x3 = np.concatenate([np.random.rand(100, 2),
np.random.rand(25, 2)/4+0.4])
y = np.array([0]*100+[1]*25)
# 最大のF値を与えるk,athの算出
K = np.arange(1, 10)
Ath = np.arange(-3, 3, 0.2)
F = np.zeros((len(K), len(Ath)))
for i, k in enumerate(K):
for j, a in enumerate(Ath):
F[i, j] = calc_TPTF(np.eye(2), x3, y, k, a)[2]
max_id = np.where(F==np.max(F))
k_best = K[min(max_id[0])]
ath_best = Ath[max(max_id[1])]
print(k_best)
print(ath_best)
# 未知のデータ
x4 = np.array([[0.3, 0.6],
[0.5, 0.4]])
# 異常判定
test_ids = near_k_id(x3, x4, np.eye(2), k=k_best)
y_test_pred = calc_a(y, ath=ath_best, ids=test_ids)
for i in range(len(x4)):
print(x4[i,:], ": ", y_test_pred[i])
# マップ作成
_x = np.arange(-0.1,1.1,0.01)
_y = np.arange(-0.1,1.1,0.01)
xx, yy = np.meshgrid(_x, _y)
XY = np.array([xx.ravel(), yy.ravel()]).T
test_ids = near_k_id(x3, XY, np.eye(2), k=k_best)
y_pred = calc_a(y, ath=ath_best, ids=test_ids)
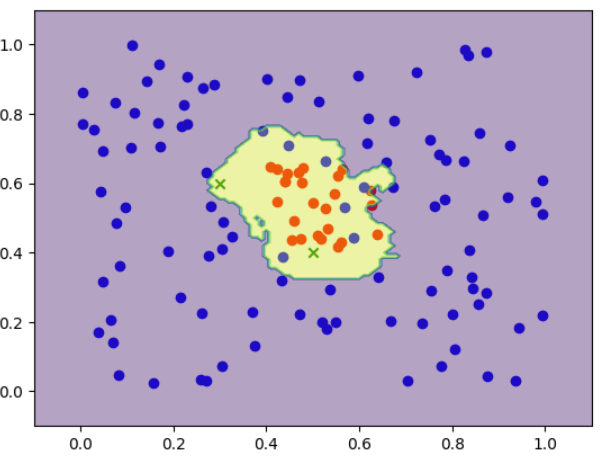
# 描画
plt.scatter(x3[y==1,0], x3[y==1,1], color='red');
plt.scatter(x3[y==0,0], x3[y==0,1], color='blue');
plt.scatter(x4[:,0], x4[:,1], color='green', marker='x');
plt.contourf(xx,yy,y_pred.reshape(121,121), alpha=.4)
マージン最大化近傍法
計量学習
異常か正常かのラベル付きデータ$D={(\boldsymbol{x}^{(n)}, y^{(n)}|n=1,\cdots,N)}$があるとする。
ユークリッド距離の代わりに、$M×M$半正定値行列$A$を使って、2つの標本間の距離の2乗を
$$
d^2_A(\boldsymbol{x}',\boldsymbol{x}'')=(\boldsymbol{x}'-\boldsymbol{x}'')^TA(\boldsymbol{x}'-\boldsymbol{x}'')
$$
のように置く。
行列$A$をデータから学習する手法を一般に 計量学習(またはリーマン計量) と呼ぶ。
Aが$M$次元単位行列$I_M$であればユークリッド距離の2乗と同じである。
考えるべき点は
- 同一ラベルに属する標本をなるべく密集させること
- 異なるラベルに属する標本をできる限り引き離すこと
の2点である。
マージン最大化近傍法の目的関数
この2つの条件を実装したものが、マージン最大化近傍法という計量学習の手法である。
def make_ellipse(x, y, a, b, theta, phi):
e = np.concatenate([[x + a * np.cos(theta)], [y + b * np.sin(theta)]], axis=0)
return np.dot(np.matrix([[np.cos(phi), -np.sin(phi)], [np.sin(phi), np.cos(phi)]]), e).T
p1 = np.array([[0, 0],
[0,0.5],
[0.5, 1],
[-0.5, -0.5]])
p2 = np.array([[-0.3, 0.3],
[-0.2, -0.5]])
c1 = make_circle(0, 0, r=np.sqrt(0.5**2+1), theta=theta)
fig ,axes = plt.subplots(nrows=1, ncols=2, figsize=(5*2, 3*1))
axes[0].scatter(p1[:,0], p1[:,1]);
axes[0].scatter(p2[:,0], p2[:,1]);
axes[0].plot(c1[:,0], c1[:,1], '--');
c2 = make_ellipse(0, 0, 0.4, 1.2, theta=theta, phi=-np.pi/6)
p2 = np.array([[-0.3, 0.5],
[-0.2, -1.2]])
axes[1].scatter(p1[:,0], p1[:,1]);
axes[1].scatter(p2[:,0], p2[:,1]);
axes[1].plot(c2[:,0], c2[:,1], '--');
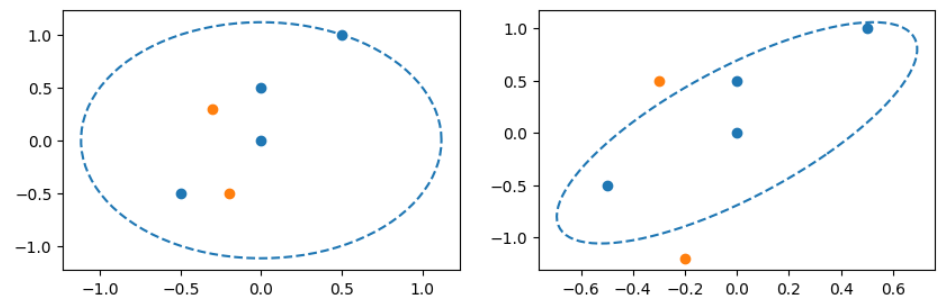
近傍数$k$をパラメータとして与え、$A=I_M$としたときの距離の定義を用いて、$D$に属する任意の標本$\boldsymbol{x}^{(n)}$の、
同一ラベルに属する$k$個の正近傍標本を求める。
それを$N^{(n)}$と表し、標的近傍と呼ぶ。(図では$k=3$の場合を示している。)
同一ラベルの標本をなるべく密集させるという条件は、
$$
\psi_1^{(n)}(A)=\sum_{i\in N^{(n)}}d^2_A(\boldsymbol{x}^{(n)},\boldsymbol{x}^{(i)})
$$
をなるべく小さくする、と表現できる。
リーマン計量$A$を求めるための最適化問題は次のように書ける。
$$
\Psi(A)=\frac{1}{N}\sum_{n=1}^N\bigl[(1-\mu)\psi_1^{(n)}(A)+\mu\psi_2^{(n)}(A) \bigr]→最小化\
subject\ to A:半正定値行列
$$
勾配法による最適化
マージン最大化近傍法の最適化問題は半正定値計画であるが、勾配法と固有値問題を組み合わせて解くことができる。
$[・]+$は微分できない関数であるので、微分可能な目的関数に対する勾配法との違いを強調して劣勾配法と呼ぶ。
この場合、$[・]+$の中に正の項しか入らないようにすれば、普通の勾配法と同様になる。
今$N$次元空間における$i$方向の単位ベクトルを$\boldsymbol{e}_i$とかき、これを使って
C^{(i,j)}=(\boldsymbol{e}_i-\boldsymbol{e}_j)(\boldsymbol{e}_i-\boldsymbol{e}_j)^T
という行列を定義する。
\frac{\partial \Psi(A)}{\partial A}=\frac{1}{N}XCX^T\\
C=\sum_{n=1}^N\sum_{j\in N^{(n)}}\bigl\{(1-\mu)C^{(n,j)}+\mu\sum_{l\in N_{n,j}}(C^{(n,j)}-C^{(n,l)}) \bigr\}
ただし、$X$はデータ行列で、$X=[\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}]$のように定義される。
また、集合は$N_{n,j}$は、$\boldsymbol{x}^{(n)}$および$\boldsymbol{x}^{(j)}$と異なるラベルを持ち、
なおかつ$1+d_A^2(\boldsymbol{x}^{(n)},\boldsymbol{x}^{(j)})-d_A^2(\boldsymbol{x}^{(n)},\boldsymbol{x}^{(l)})>0$となる標本の添え字$l$の集合である。
$A$が更新されたら、固有値分解$A=U\Gamma U^T$を行い、
A←U[\Gamma]_+ U^T
のようにさらに$A$を更新する。
ここで、$[\Gamma]_+$は負の固有値を0で置き換えることを意味する。
アルゴリズムを示す。
標本数の不均衡の是正は、ブートストラップ法により、
少数クラスの見かけ上の標本数を増やすか、多数クラスの標本を間引くかすることでおこなうのが一般的である。
- 初期化: 近傍数$k$、係数$\mu$、ステップ幅の初期値$\eta_0$を与える
$A=I_M$と置く。各クラスの標本数の不均衡がある場合は前処理で是正しておく。- 反復: 次の更新式を実行する
実行のたびに収束を判定し、収束していない場合、ステップ幅$\nu$を更新して繰り返す
$$
A←A-\eta\frac{\partial \Psi(A)}{\partial A}\
A=U\Gamma U^T\
A←U[\Gamma]_+ U^T
$$- 収束した$A^*$を出力する
def make_Cij(N):
"""行列Cijを作成
"""
c = np.matrix(np.eye(N))
Cij = np.array([[(c[:,i]-c[:,j])@(c[:,i]-c[:,j]).T for j in np.arange(N)] for i in np.arange(N)])
return Cij
def dA2(x1, x2, A):
"""距離の計算
"""
return (x1-x2)@A@(x1-x2).T
def recalc_A(A, x, y, k, mu, eta):
"""Aを更新する
"""
# 多数クラスを間引いて標本数を揃える
min_count = min(np.bincount(y))
x_bs = np.concatenate([x[y==label][np.random.choice(np.arange(np.sum(y==label)), min_count)] for label in np.unique(y)])
y_bs = np.concatenate([[label]*min_count for label in np.unique(y)])
N = len(x_bs)
# 各標本同士の距離
d = np.array([[dA2(x_bs[i],x_bs[j], A) for j in np.arange(N)] for i in np.arange(N)])
Nn = near_k_id(x_bs, x_bs, np.eye(M), k=k)
Cij = make_Cij(N)
# 行列Cを計算
C = np.matrix(np.zeros((N,N)))
for n in np.arange(N):
for j in Nn[n]:
Nnj = np.where((d[n] < d[n][j]+1)&(d[n]!=0)&(y_bs!=y_bs[n]))[0]
C += (1-mu)*Cij[n,j] + mu * np.sum((Cij[n,j]-Cij[n,Nnj]), axis=0)
# 勾配を計算
dpsi = np.dot(np.dot(x_bs.T, C), x_bs)/N
# 更新の実行
A_new = A - dpsi
U = np.linalg.eig(A_new)[1]
G = np.linalg.eig(A_new)[0]
G=np.diag(G)
G[G<0]=0
A_new = U@G@np.linalg.inv(U)
return A_new
def update_A(x3, y, k, mu, eta):
"""Aの反復計算
"""
A = np.eye(M)
for i in np.arange(100):
A_new = recalc_A(A, x3, y, k, mu, eta)
# 収束するまで繰り返す
if np.linalg.det(A-A_new) < 0.0001:
A = A_new
break
A = A_new
return np.array(A)
M = 2
mu = 0.5
eta = 0.1
# 近傍点の数と閾値をF値から決める
K = np.arange(3, 10)
Ath = np.arange(0, 2, 0.1)
F = np.zeros((len(K), len(Ath)))
for i, k in enumerate(K):
# Aの計算
A = update_A(x3, y, k, mu, eta)
for j, a in enumerate(Ath):
F[i, j] = calc_TPTF(A, x3, y, k, a)[2]
max_id = np.where(F==np.max(F))
k_best = K[min(max_id[0])]
ath_best = Ath[max(max_id[1])]
A_best = update_A(x3, y, k_best, mu, eta)
print(k_best)
print(ath_best)
# 未知の点
x4 = np.array([[0.3, 0.6],
[0.5, 0.4],
[0.55, 0.5]])
test_ids = near_k_id(x3, x4, A_best, k=k_best)
y_test_pred = calc_a(y=y, ath=ath_best, ids=test_ids)
for i in range(len(x4)):
print(x4[i,:], ": ", y_test_pred[i])
_x = np.arange(-0.1,1.1,0.01)
_y = np.arange(-0.1,1.1,0.01)
xx, yy = np.meshgrid(_x, _y)
XY = np.array([xx.ravel(), yy.ravel()]).T
test_ids = near_k_id(x3, XY, A_best, k=k_best)
y_pred = calc_a(y=y, ath=ath_best, ids=test_ids)
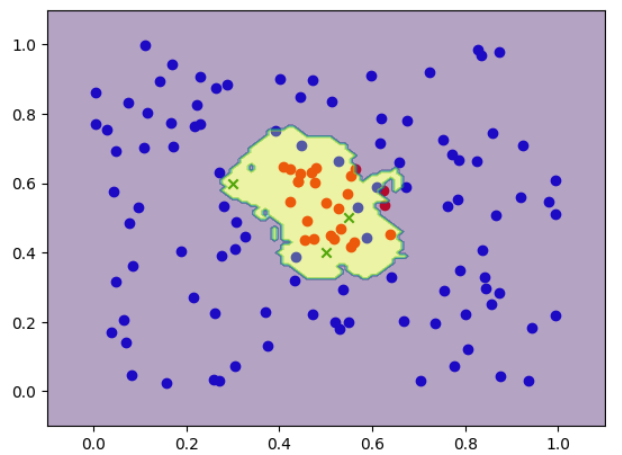
plt.scatter(x3[y==1,0], x3[y==1,1], color='red');
plt.scatter(x3[y==0,0], x3[y==0,1], color='blue');
plt.scatter(x4[:,0], x4[:,1], color='green', marker='x');
plt.contourf(xx,yy,y_pred.reshape(121,121), alpha=.4)
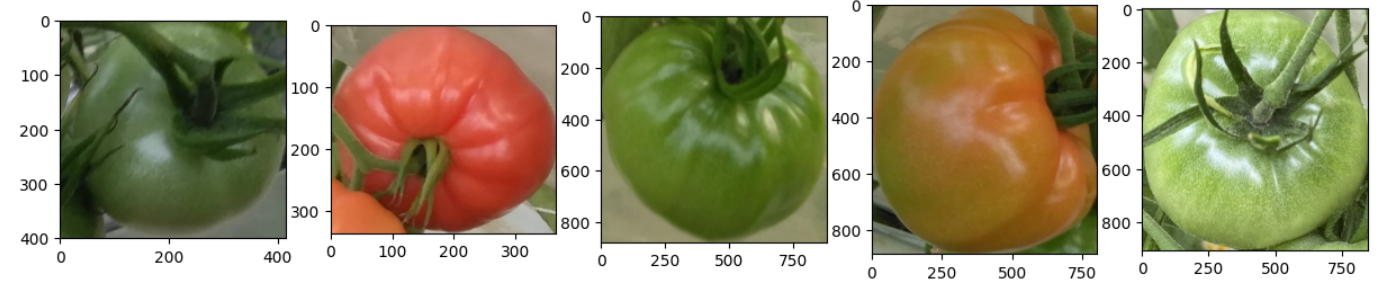
画像データの分類で試してみます。
トマトの画像データの赤いものを正常、青いものを異常とします。
(結局は分類モデルを作成したことと一緒になりそうです。)
データは以下サイトからダウンロードしたものです。
利用に関してはサイト内の注意を見てください。
今回は例のため、赤と緑の2成分を使用します。
import pandas as pd
import json
import cv2
main_dir = 'laboro_tomato_big/laboro_big/'
image_dir = main_dir+'train/'
json_file = open(main_dir+'annotations/train.json', 'r')
json_dict = json.load(json_file)
data = pd.merge(pd.DataFrame(json_dict['images'])[['file_name', 'id']], pd.DataFrame(json_dict['annotations'])[['image_id', 'bbox', 'category_id']], left_on='id', right_on='image_id')
df = pd.DataFrame()
for f in data['file_name'].unique():
img = cv2.imread(image_dir+f)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
for b in data.loc[data['file_name']==f, 'bbox']:
x1,y1, width, height = b
img_bbox = img[int(y1):int(y1)+int(height),int(x1):int(x1)+int(width)]
r = np.mean(img_bbox[:,:,0])
g = np.mean(img_bbox[:,:,1])
b = np.mean(img_bbox[:,:,2])
df = pd.concat([df,pd.DataFrame({'R':[r], 'G':[g], 'B':[b]})], axis=0)
data = pd.concat([data, df.reset_index(drop=True)], axis=1)
fig, ax = plt.subplots(1,5, figsize=(15,5))
for i, f in enumerate(data['file_name'].unique()[10:15]):
img = cv2.imread(image_dir+f)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
for b in data.loc[data['file_name']==f, 'bbox']:
x1,y1, width, height = b
img_bbox = img[int(y1):int(y1)+int(height),int(x1):int(x1)+int(width)]
ax[i].imshow(img_bbox)
tmp = data[data['category_id'].apply(lambda x: x in [1,3])].reset_index(drop=True)
tmp = tmp.sample(n=200)
tmp['y'] = (tmp['category_id']<=1).astype(int)
x_tomato = np.array(tmp[['R','G']])
x_tomato = (x_tomato-np.mean(x_tomato, axis=0))/ np.std(x_tomato, axis=0)
y = np.array(tmp['y'])
N = len(x_tomato)
M = 2
mu = 0.5
eta = 0.1
# 近傍点の数と閾値をF値から決める
K = np.arange(3, 10)
Ath = np.arange(0, 2, 0.1)
F = np.zeros((len(K), len(Ath)))
for i, k in enumerate(K):
# Aの計算
A = update_A(x_tomato, y, k, mu, eta)
for j, a in enumerate(Ath):
F[i, j] = calc_TPTF(A, x_tomato, y, k, a)[2]
max_id = np.where(F==np.max(F))
k_best = K[min(max_id[0])]
ath_best = Ath[max(max_id[1])]
A_best = update_A(x_tomato, y, k_best, mu, eta)
print(k_best)
print(ath_best)
import japanize_matplotlib
_tmp = data[data['category_id'].apply(lambda x: x in [1,3])].reset_index(drop=True)
_label = (_tmp['category_id']<=1).astype(int)
_x_tomato = np.array(_tmp[['R','G']])
_x_tomato = (_x_tomato-np.mean(_x_tomato, axis=0))/ np.std(_x_tomato, axis=0)
_x = np.arange(-3,3,0.01)
_y = np.arange(-3,3,0.01)
xx, yy = np.meshgrid(_x, _y)
XY = np.array([xx.ravel(), yy.ravel()]).T
test_ids = near_k_id(x_tomato, XY, A_best, k=k_best)
y_pred = calc_a(y=y, ath=ath_best, ids=test_ids)
colors=['red','green']
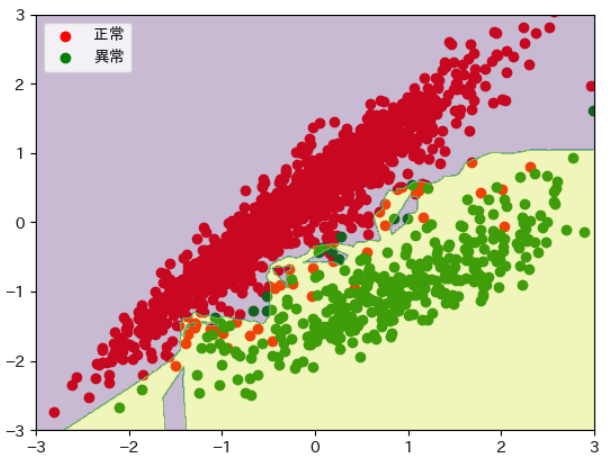
for i in range(2):
plt.scatter(_x_tomato[_label==i,0],_x_tomato[_label==i,1], color=colors[i])
plt.legend(['正常', '異常'])
plt.contourf(xx,yy,y_pred.reshape(600,600), alpha=.3)
plt.xlim(-3,3)
plt.ylim(-3,3)
境界線が引けそうな場合は他の方法でよいかもしれません。
距離の計算があるためか、処理に時間がかかります。
例ということでご了承ください。
以上となります。
次回
混合分布モデルによる逐次更新型異常検知