とても有名な「統計学入門」をpythonで実装しながら読んでいきます。
本をしっかり読むことと実装の勉強が目的ですので説明が不足していたりします。
また、実装方法に関してはベストなものではないと思いますのでご了承ください。
前回
仮説検定
回帰分析
回帰分析は、2変数$X,Y$のデータがあるとき回帰方程式と呼ばれる説明の関係を定量的に表す式を求めることを目的としている。
説明される変数を$Y$で表し、これを従属変数、被説明変数、内生変数などと呼ぶ。
また、説明する変数を$X$で表し、独立変数、説明変数、外生変数などと呼ぶ。
回帰分析の目的は、$X$と$Y$との定量的な関係の構造(モデル)を求めることである。
説明変数$X$、被説明変数$Y$とし、
たとえば、
$$
y=\beta_1+\beta_2x
$$
とする。
これは$y$の$x$上への回帰方程式、回帰関数などと呼ばれるが、$y$が$x$の線形関数である場合を線形関数、それ以外のものを非線形関数と呼ぶ。
ここで、ばらつきの部分を$\varepsilon_i$とすると、母集団において、
$$
Y_i=\beta_1+\beta_2X_i+\varepsilon_i,\hspace{3mm}(i=1,\cdots,n)
$$
となる。
このモデルを母回帰方程式と呼び、$\beta_1,\beta_2$を母(偏)回帰係数という。
これは母集団の値であるから一般にはわからない。
これについて推定、検定するのが回帰分析である。
ただし、$X_i$は確率変数ではなく、すでに確定した値をとっている。
また、$\varepsilon_i$は誤差項と呼ばれ、次の三つの条件を満たす確率変数である。
- 期待値は0:$E(\varepsilon_i)=0,\hspace{3mm}i=1,\cdots,n$
- 分散は一定で$\sigma^2$:$V(\varepsilon_i)=\sigma^2,\hspace{3mm}i=1,\cdots,n$
- 異なった誤差項は無相関:$i\neq j$ならば$Cov(\varepsilon_i,\varepsilon_j)=E(\varepsilon_i\varepsilon_j)=0$
このことは、
$$
E(Y_i)=\beta_1+\beta_2X_i,\hspace{3mm}(i=1,\cdots,n)
$$
であることを意味している。
回帰係数の推定
最小二乗法による回帰係数の推定
母回帰係数$\beta_1,\beta_2$の推定を考える。
$X_i$によって説明できない誤差項は、
$$
\varepsilon_i=Y_i-(\beta_1+\beta_2X_i),\hspace{3mm}i=1,\cdots,n
$$
である。
$\varepsilon_i$の符号の影響を取り除くために
$$
S=\sum\varepsilon_i^2=\sum \{Y_i-(\beta_1+\beta_2X_i) \}^2
$$
とすると、$S$は$Y_i$が$X_i$で説明できない部分の総和を表しているから、できるだけ小さいほうが望ましいと考えられる。
$S$を最小にする$\hat{\beta}_1,\hat{\beta}_2$を$\beta_1,\beta_2$の推定量とする。
この考え方に基づく推定方法を最小二乗法と呼び、$\hat{\beta}_1,\hat{\beta}_2$を最小二乗推定量という。
$S$を最小にする$\hat{\beta}_1,\hat{\beta}_2$は、一次の偏微分を0とおいた二つの方程式
$$
\frac{\partial S}{\partial \beta_1}=-2\sum(Y_i-\beta_1-\beta_2X_i)=0\\
\frac{\partial S}{\partial \beta_2}=-2\sum(Y_i-\beta_1-\beta_2X_i)X_i=0
$$
を解くことで求めることができる。
これを整理すると、
$$
n\beta_1+(\sum X_i)\beta_2=\sum Y_i\\
(\sum X_i)\beta_1+(\sum X_i^2)\beta_2=\sum X_iY_i
$$
を得る。これを正規方程式という。
これを解くと、$\bar{X},\bar{Y}$をそれそれ$X_i,Y_i$の標本平均として
$$
\hat{\beta}_2=\frac{\sum(X_i-\bar{X})(Y_i-\bar{Y})}{\sum(X_i-\bar{X})^2}\\
\hat{\beta}_1=\bar{Y}-\hat{\beta}_2\bar{X}
$$
で与えられる。
$\hat{\beta}_1,\hat{\beta}_2$は標本(偏)回帰係数と呼ばれる。
また、
$$
Y=\hat{\beta}_1+\hat{\beta}_2X_i
$$
を標本回帰方程式、標本回帰直線と呼ぶ。
$\hat{Y}_i=\hat{\beta}_1+\hat{\beta}_2X_i$は$E(Y_i)$の推定量となるが、これを回帰値ということもある。
実測値$Y_i$の、回帰方程式に定められた回帰値$\hat{Y}_i$からのずれ
$$
\hat{e}_i=Y_i-\hat{Y}_i=Y_i-\hat{\beta}_1-\hat{\beta}_2X_i
$$
は$X$で説明されずに残った分であり、回帰残差と呼ばれる。
$\hat{e}_i$に関して、
$$
\sum\hat{e}_i=0\\
\sum \hat{e}_iX_i=0
$$
が成り立つ。
誤差項$\varepsilon_i$の分散$\sigma^2$は回帰方程式のあてはまりのよさを表すが、
$$
s^2=\sum \hat{e}_i^2\ /\ (n-2)
$$
で推定される。($n-2$で割られるのは、上の2つの条件のためである。)
この$s$を推定値の標準誤差ということがある。
ここで、各変数からその標本平均、標本標準偏差を使って標準化し、$(X_i-\bar{X})\ /\ s_x,(Y_i-\bar{Y})\ /\ s_y$について回帰分析を行うことも多い。
この場合の偏回帰係数を標準化(偏)回帰係数という。切片の推定量は常に0になり、傾きの値は相関係数と一致する。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
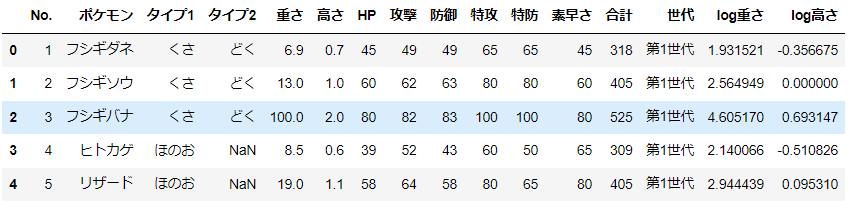
d = pd.read_csv('pokemon_for_stats.csv').iloc[:,1:]
gen = ["第1世代"]*151+["第2世代"]*100+["第3世代"]*135+["第4世代"]*107+["第5世代"]*156+["第6世代"]*72+["第7世代"]*88+["第8世代"]*89
d['世代'] = gen
num_cols = ['重さ','高さ','HP','攻撃','防御','特攻','特防','素早さ','合計']
d['log重さ'] = np.log(d['重さ'])
d['log高さ'] = np.log(d['高さ'])
d.head()
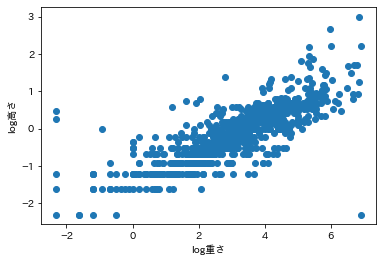
plt.plot(d['log重さ'], d['log高さ'], 'o');
plt.xlabel('log重さ');
plt.ylabel('log高さ');
x = d['log重さ'].values
y = d['log高さ'].values
# 回帰係数の計算
beta2 = np.sum((x - x.mean())*(y-y.mean())) / np.sum((x - x.mean())**2)
beta1 = y.mean() - beta2 * x.mean()
print('beta1: ', beta1)
print('beta2: ', beta2)
# プロット
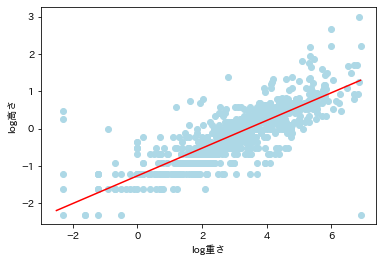
xx = np.arange(-2.5,7,0.1)
plt.plot(x, y, 'o', color='lightblue');
plt.plot(xx, beta1+beta2*xx, color='red');
plt.xlabel('log重さ');
plt.ylabel('log高さ');
beta1: -1.2667653595569675
beta2: 0.3713921127472261
# 誤差の分散
s2 = np.sum((beta1+beta2*x - y)**2)/(len(x)-2)
print('s2: ', s2)
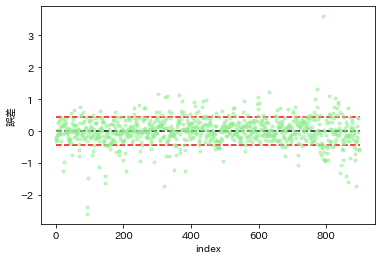
# 回帰残差のプロット
plt.plot(beta1+beta2*x - y, 'o', color='lightgreen', markersize=3,alpha=.5);
plt.hlines(0, 0, 900, color='black', linestyle='--');
plt.hlines([np.sqrt(s2),-np.sqrt(s2)], 0, 900, color='red', linestyle='--');
plt.xlabel('index');
plt.ylabel('誤差');
s2: 0.1843265974152541
回帰方程式のあてはまりの良さと決定係数
モデルのあてはまりの良さをはかる基準として一般に使われるのが、決定係数$\eta^2$である。
$Y_i$のばらつきの総和は$\sum(Y_i-\bar{Y})^2$であるが、これは回帰方程式により説明できる$\sum(\hat{Y}_i-\bar{Y})^2$と、説明できない$\sum\hat{e}_i^2=\sum(Y_i-\hat{Y})^2$である。
$$
\sum(Y_i-\bar{Y})^2=\sum(\hat{Y}_i-\bar{Y})^2+\sum\hat{e}_i^2
$$
となっている。
決定係数$\eta^2$は、$Y_i$に変動のうち$X_i$の回帰方程式で説明できる変動の割合であり、
$$
\eta^2=1-\frac{\sum\hat{e}_i^2}{\sum(Y_i-\bar{Y})^2}=\frac{\sum(\hat{Y}_i-\bar{Y})^2}{\sum(Y_i-\bar{Y})^2}
$$
で定義される。
$\eta^2$は0から1の間の数であり、$X_i$が$Y_i$を完全に説明しているとき、すべての$i$で$\hat{e}=0$で、$Y_i$と$X_i$をグラフに描けば観測点は一直線上に乗り$\eta^2=1$となる。
線形の回帰式の場合、決定係数は、
$$
\eta^2=r^2
$$
となることがわかっている。
# 決定係数
eta2 = np.sum((beta1+beta2*x - y.mean())**2)/ np.sum((y - y.mean())**2)
r2 = np.corrcoef(beta1+beta2*x, y)[0,1]**2
print('eta2: ', eta2)
print('r2: ', r2)
eta2: 0.6543722102350107
r2: 0.654372210235011
偏回帰係数の統計的推測
偏回帰係数の標本分布
誤差項$\varepsilon_1,\cdots,\varepsilon_n$が独立で共通の正規分布$N(0,\sigma^2)$に従うとする。
標本回帰係数$\hat{\beta}_2$は、$\varepsilon_i$の線形関数であるから、その標本分布はふたたび正規分布となるが、
$$
E(\hat{\beta}_1)=\beta_1,\hspace{5mm}E(\hat{\beta}_2)=\beta_2\
V(\hat{\beta}_1)=\frac{\sigma^2\sum X_i^2}{n\sum(X_i-\bar{X})^2},\hspace{5mm}V(\hat{\beta}_2)=\frac{\sigma^2}{\sum(X_i-\bar{X})^2}
$$
によってその平均、分散も併せて示せば
$$
N\biggl(\beta_2, \frac{\sigma^2}{\sum(X_i-\bar{X})^2} \biggr)
$$
となる。
$\sigma^2$は未知であるから、回帰残差$\hat{e}_i=Y_i-\hat{\beta}_1-\hat{\beta}_2X_i$を使って、$s^2=\sum \hat{e}_i^2\ /\ (n-2)$のように標本から推定する。
また、
$$
s.e.=\sqrt{s^2}=\sqrt{\sum e_i^2\ /\ (n-2)}
$$
という推定値の標準誤差を用いて、$\hat{\beta}_2$の標準誤差の推定量($\hat{\beta}_2$の標準誤差)を、
$$
s.e.(\hat{\beta}_2)=\frac{s.e.}{\sqrt{\sum(X_i-\bar{X})^2}}
$$
とすると、この$s.e.(\hat{\beta}_2)$が$\beta_2$の検定、推定を行うときの基準となる。
実際、標準化した$(\hat{\beta}_2-\beta_2)\ /\ \sqrt{\sigma^2\ /\ \sum(X_i-\bar{X})^2}$は、標準正規分布に従うが、$\sigma^2$を$s^2$に置き換えた、
$$
t_2=\frac{\hat{\beta}_2-\beta_2}{s.e.(\hat{\beta}_2)}
$$
は、自由度$n-2$のt分布$t(n-2)$に従う。
また、$\hat{\beta}_1$の標本分布は
$$
N\biggl(\beta_1, \frac{\sigma^2\sum X_i^2}{n\sum(X_i-\bar{X})^2} \biggr)
$$
であり、標準誤差は、
$$
s.e.(\hat{\beta}_1)=s.e.\sqrt{\frac{\sum X_i^2}{n\sum (X_i-\bar{X})^2}}
$$
である。また、
$$
t_1=\frac{\hat{\beta}_1-\beta_1}{s.e.(\hat{\beta}_1)}
$$
も、自由度$n-2$のt分布$t(n-2)$に従う。
偏回帰係数の検定
帰無仮説を、
$$
H_0:\beta_2=a\ (aは指定された定数)
$$
とし、対立仮説を
$$
H_1:\beta_2\neq aまたはH_1:\beta_2>a
$$
とする。
標本から$\hat{\beta}_2,s.e.(\hat{\beta_2})$を計算し、
t_2=\frac{\hat{\beta}_2-\beta_2}{s.e.(\hat{\beta}_2)}
を求める。
次に自由度$n-2$のt分布$t(n-2)$ のパーセント点を求め、両側検定では $|t_2|\geq t_{\alpha/2}(n-2)$ のとき、片側検定では$t_2\geq t_{\alpha}(n-2)$のとき、帰無仮説を棄却し、それ以外は棄却しない。
$X$が$Y$を説明することができるかどうかの検定、すなわち$H_0:\beta_2=0$の検定が特に重要である。
from scipy import stats
# サンプル数
n = 40
# 回帰係数のリストを作る
beta1_list = []
beta2_list = []
# 300回実験
for _ in range(300):
d_sample = d.sample(n)
x = d_sample['log重さ'].values
y = d_sample['log高さ'].values
# 回帰係数の計算
beta2 = np.sum((x - x.mean())*(y-y.mean())) / np.sum((x - x.mean())**2)
beta1 = y.mean() - beta2 * x.mean()
# リストに追加
beta2_list.append(beta2)
beta1_list.append(beta1)
# 標本平均
mean_beta2 = np.mean(beta2_list)
mean_beta1 = np.mean(beta1_list)
# 標本分散
s2 = np.sum((mean_beta1+mean_beta2*x - y)**2)/(len(x)-2)
# 標準誤差
se = np.sqrt(s2)
# 各係数の標準誤差
se_beta2 = se/np.sqrt(np.sum((x-x.mean())**2))
se_beta1 = np.sqrt(np.sum(x**2)/(n*np.sum((x-x.mean())**2)))
# 正規分布
xx = np.arange(-2.3,2.3,0.01)
norm_dist1 = stats.norm.pdf(xx, mean_beta1, se_beta1)
norm_dist2 = stats.norm.pdf(xx, mean_beta2, se_beta2)
# プロット
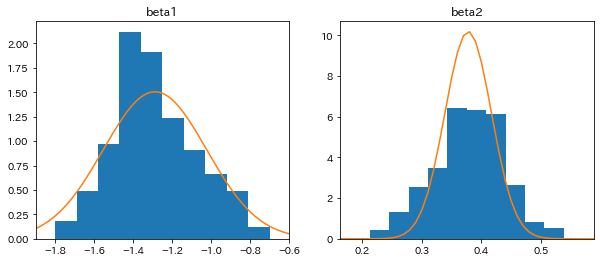
fig, ax = plt.subplots(1,2,figsize=(10,4))
ax[0].hist(beta1_list, density=True);
ax[0].plot(xx,norm_dist1);
ax[0].set_xlim(np.min(beta1_list)-0.1, np.max(beta1_list)+0.1);
ax[0].set_title('beta1')
ax[1].hist(beta2_list, density=True);
ax[1].plot(xx,norm_dist2);
ax[1].set_xlim(np.min(beta2_list)-0.05, np.max(beta2_list)+0.05);
ax[1].set_title('beta2')
Text(0.5, 1.0, 'beta2')
alpha = 0.05
print('beta1: ', beta1)
print('beta2: ', beta2)
# 各係数のt統計量
t1 = beta1 / se_beta1
t2 = beta2 / se_beta2
print('t1 :', t1)
print('t2 :', t2)
# 各係数のp値
p1 = stats.t.sf(np.abs(t1), df=n-2)*2
p2 = stats.t.sf(np.abs(t2), df=n-2)*2
print('p1 :', p1)
print('p2 :', p2)
# パーセント点
t0025 = stats.t.ppf(alpha/2, n-2)
t975 = stats.t.ppf(1-alpha/2, n-2)
print('t 0.025 - 0.975: ', t0025, t975)
# 判定
print('beta1 judge: ', p1<alpha)
print('beta2 judge: ', p2<alpha)
beta1: -1.0331694110662104
beta2: 0.29939240701398884
t1 : -3.896117390878051
t2 : 7.653520569767128
p1 : 0.00038384522434977173
p2 : 3.2682464834681654e-09
t 0.025 - 0.975: -2.0243941645751367 2.024394164575136
beta1 judge: True
beta2 judge: True
重回帰分析
重回帰分析は複数の説明変数を含むもので、母集団において
$$
Y_i=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+\varepsilon_i\hspace{3mm}(i=1,\cdots,n)
$$
となるモデルである。また、$\beta_1,\beta_2,\cdots,\beta_k$は、ある説明変数の(他の説明変数の影響を除いた、純粋の)影響を表わしている。
なお、定数$X_{1i}=1$が$\beta_1$の直後に省略されている。
重回帰方程式は、$k$個の未知の母(偏)回帰係数$\beta_1,\cdots,\beta_k$を含むが、その推定には、最小二乗法が用いられる。誤差項は、
$$
\varepsilon_i=Y_i-(\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki})
$$
であるが、その平方和
$$
S=\sum\varepsilon_1^2
$$
を考えそれを最小にする。
$S$を最小にする$\beta_1,\cdots,\beta_k$は、一次の偏微分を0と置いた$k$個の連立方程式
$$
\frac{\partial S}{\partial \beta_1}=0,\hspace{3mm},\frac{\partial S}{\partial \beta_2}=0,\hspace{3mm},\cdots,\frac{\partial S}{\partial \beta_k}=0
$$
を解くことによって求められる。
この解を$\hat{\beta}_1,\hat{\beta}_2,\cdots,\hat{\beta}_k$とすれば、これらが求めるものであって、これらを標本(偏)回帰係数という。
ここで得られた、
$$
Y=\hat{\beta}_1+\hat{\beta}_2X_2+\hat{\beta}_3X_3+\cdots+\hat{\beta}_kX_k
$$
を標本重回帰方程式という。また、各$i$の $E(Y_i)$は、
\hat{Y}_i=\hat{\beta}_{1i}+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki}
で推定される。これを回帰値という。
単回帰分析と同様、
$$
\sum(Y_i-\bar{Y})^2=\sum(\hat{Y}_i-\bar{Y})^2+\sum\hat{e}_i^2
$$
と表すことができる。
モデルのあてはまりの良さを表す決定係数$\eta^2$は、
$$
\eta^2=\frac{\sum(\hat{Y}_i-\bar{Y})^2}{\sum(Y_i-\bar{Y})^2}=1-\frac{\sum\hat{e}_i^2}{\sum(Y_i-\bar{Y})^2}
$$
で定義される。決定係数の正の平方根を重相関係数といい、$R$で表す。$\eta^2=R^2$となる。
単回帰分析に準じて、誤差項$\varepsilon_i$の分散$\sigma^2$を、
$$
s^2=\sum\hat{e}_i^2\ /\ (n-k)
$$
で推定する。
この$s$の推定値の標準誤差$s.e.$として、これから$\hat{\beta}_i$の標準誤差$s.e.(\hat{\beta}_i)$などが求められる。
$$
t_i=\frac{\hat{\beta}_i-\beta_i}{s.e.(\hat{\beta}_i)}
$$
は、自由度$n-k$のt分布$t(n-k)$に従う。
重回帰分析では複数の説明変数があるので、いくつかの回帰係数についての仮説を同時に検定したい場合がある。
このような場合では、次に述べるF検定を用いる。
- $H_0(\beta_i=0)$が正しいとして、重回帰方程式を推定し、回帰残差の平方和$\sum \hat{e}_i^2$を$S_0$とする
- すべての説明変数を含む重回帰方程式を推定し、その回帰残差の平方和$\sum e_i'^{2}$を$S_1$とする。これは$H_0$が成立していない場合に相当する。
- 帰無仮説に含まれる制約式の数を$p$とすると、統計量
$$
F=\frac{(S_0-S_1)\ /\ p}{S_1\ /\ (n-k)}
$$
は、帰無仮説が正しい場合、自由度$(p,n-k)$のF分布$F(p, n-k)$に従うことが知られている。
したがって、このF-統計量を計算し、
$$
F\geq F_{\alpha}(p,n-k)
$$
のときに帰無仮説を棄却し、それ以外は棄却しない。
とくに、$X_2,\cdots,X_k$のすべてが$Y$を説明しないという帰無仮説
$$
H_0:\beta_2=\cdots=\beta_k=0
$$
を$X_2,\cdots,X_k$のどれか一つは説明しているという対立仮説
$$
H_1:\beta_2,\beta_3,\cdots,\beta_kの少なくとも一つが0でない
$$
に対し検定する場合は、$S_0=\sum(Y_i-\bar{Y})^2,p=k-1$であるから、これらの値からF値を計算する。
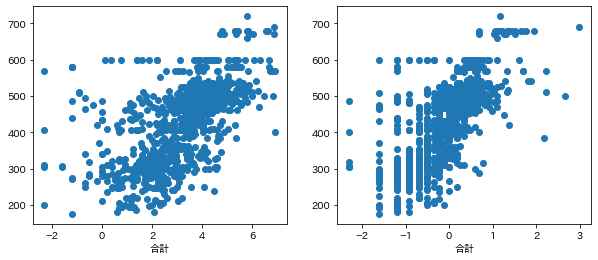
fig, ax = plt.subplots(1,2,figsize=(10,4))
ax[0].plot(d['log重さ'], d['合計'], 'o');
ax[0].set_xlabel('log重さ');
ax[0].set_xlabel('合計');
ax[1].plot(d['log高さ'], d['合計'], 'o');
ax[1].set_xlabel('log高さ');
ax[1].set_xlabel('合計');
alpha = 0.05
n = len(d)
k = 3
X = d[['log重さ', 'log高さ']].values
X = np.concatenate([np.ones((n,1)), X],axis=1)
y = d['合計'].values.reshape(-1,1)
# 係数行列
A = np.linalg.inv(X.T@X)@X.T@y
print('A: ', A)
# 予測値
y_pred = X@A
# 決定係数
eta2 = np.sum((y_pred-y.mean())**2) / np.sum((y-y.mean())**2)
print('r2: ', eta2)
# 残差の計算
S1 = np.sum((y_pred-y)**2)
S0 = np.sum((y-y.mean())**2)
# F統計量
F = ((S0-S1)/(k-1)) / (S1/(n-k))
print('F value: ', F)
# p値
p = stats.f.sf(np.abs(F), dfn=k-1, dfd=n-k)
print('p value: ', p)
# パーセント点
f095 = stats.f.ppf(1-alpha, dfn=k-1, dfd=n-k)
print('F095: ', f095)
print('judge: ', p<alpha)
A: [[410.79862077]
[ 7.13623642]
[ 92.78446789]]
r2: 0.47625975646128127
F value: 406.93119088273903
p value: 2.0155137059375274e-126
F095: 3.005781962311099
judge: True
この重回帰方程式は有意水準5%で採択される。
ここで、重回帰係数の計算は単回帰と同様に行おうとすると計算が複雑になるので、次のように行った。
$\boldsymbol{Y}=(y_1,\cdots,y_n)^T$、 $\boldsymbol{X}=(\boldsymbol{x_1},\cdots,\boldsymbol{x_m})$,$\boldsymbol{x_i}=(x_{i1},\cdots,x_{in})$ であり、$A$は$\boldsymbol{X}$に対する係数行列である。
$$
\boldsymbol{Y}=\boldsymbol{X}A\\
\boldsymbol{X}^T\boldsymbol{Y}=\boldsymbol{X}^T\boldsymbol{X}A\\
A=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{Y}
$$
ライブラリのstatsmodelsを使い同様に重回帰分析を行う。
import statsmodels.api as sm
df_X = sm.add_constant(d[['log重さ', 'log高さ']])
df_y = d['合計']
model = sm.OLS(df_y, df_X)
result = model.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: 合計 R-squared: 0.476
Model: OLS Adj. R-squared: 0.475
Method: Least Squares F-statistic: 406.9
Date: Thu, 05 May 2022 Prob (F-statistic): 2.02e-126
Time: 01:04:31 Log-Likelihood: -5219.3
No. Observations: 898 AIC: 1.044e+04
Df Residuals: 895 BIC: 1.046e+04
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 410.7986 9.964 41.227 0.000 391.242 430.355
log重さ 7.1362 2.895 2.465 0.014 1.455 12.818
log高さ 92.7845 6.305 14.715 0.000 80.409 105.160
==============================================================================
Omnibus: 61.921 Durbin-Watson: 1.487
Prob(Omnibus): 0.000 Jarque-Bera (JB): 106.283
Skew: 0.492 Prob(JB): 8.34e-24
Kurtosis: 4.368 Cond. No. 15.6
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
自分で計算した値とほぼ同じ値となることが確認できた。
参考書