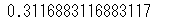pythonとopencvを使って画像処理を勉強していきます。
今回はほとんど機械学習がメインとなります。細かい理論などはここでは説明しません。
説明が不十分であったりコードが見づらい部分もあると思いますがご了承ください。
誤字や間違いは気づけば修正しますが、お気づきの点があればご指摘ください。
前回
python+opencvで画像処理の勉強8 パターン・図形・特徴の検出とマッチング
まず、画像を読み込む関数と円形度とRGB各色の平均値を計算する関数を定義しておきます。
import numpy as np
import matplotlib.pyplot as plt
import cv2
def read_img(path, s, gray=False):
img_bgr = cv2.imread(path + '/' + s)
img_rgb = cv2.cvtColor(img_bgr, cv2.COLOR_BGR2RGB)
img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_RGB2GRAY)
if gray:
return img_gray
else:
return img_rgb
def read_imges(name, path='image/', gray=False):
path = path + name
list1 = os.listdir(path)
tmp = np.array([read_img(path, s, gray=gray) for s in list1])
return tmp
def make_mask(rgb):
gray = cv2.cvtColor(rgb, cv2.COLOR_RGB2GRAY)
kernel = np.ones((3, 3), np.uint8)
ret, thresh = cv2.threshold(gray,250,255,cv2.THRESH_BINARY)
thresh = cv2.dilate(thresh, kernel, iterations = 6)
thresh = cv2.erode(thresh, kernel, iterations = 2)
mask = cv2.bitwise_not(thresh)
return mask
def calc_roundness(rgb):
thresh = make_mask(rgb)
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
cnt = contours[0]
area = cv2.contourArea(cnt)
perimeter = cv2.arcLength(cnt,True)
roundness = 4*np.pi*area / perimeter**2
return roundness
def mean_col(rgb):
gray = cv2.cvtColor(rgb, cv2.COLOR_RGB2GRAY)
mask = make_mask(rgb)
r = np.sum(rgb[:,:,0]*mask)/np.sum(mask==255)
g = np.sum(rgb[:,:,1]*mask)/np.sum(mask==255)
b = np.sum(rgb[:,:,2]*mask)/np.sum(mask==255)
return np.array([r, g, b])
パターン認識の基本的なアプローチ
パターン認識の流れ
画像処理におけるパターン認識とは、観測された画像の特徴を用いて、あらかじめ定められたクラスにその画像を識別する処理のことです。
パターン認識では、パターンを同類の画像が共通に持つ特徴の組とします。
クラスとは、同じ画像が属する集合のことで、学習のためにはクラスをあらかじめ定める必要があります。
パターン認識には、距離計算を用いるアプローチと機械学習を用いるアプローチの2つがあります。
画像からの特徴抽出
特徴抽出とは、入力画像からパターン認識に役立つ特徴を取り出す処理です。
取り出された$K$個の特徴量をそれぞれ$x_i$とすると、特徴ベクトルは$\boldsymbol{x}=(x_1,x_2,\cdots,x_K)^T$となります。
リンゴ、みかん、バナナの画像の赤みの度合いと円形度を計測し、それらを特徴とした特徴ベクトルをつくり、プロットすると図のように同じ種類のものが集まってクラスとなります。
この特徴ベクトルで構成される空間を特徴空間と呼びます。
imgs1 = read_imges('Apple')
imgs2 = read_imges('Banana')
imgs3 = read_imges('Orange')
rgb_mean1 = np.array([mean_col(s) for s in imgs1])
roundness1 = np.array([calc_roundness(s) for s in imgs1])
rgb_mean2 = np.array([mean_col(s) for s in imgs2])
roundness2 = np.array([calc_roundness(s) for s in imgs2])
rgb_mean3 = np.array([mean_col(s) for s in imgs3])
roundness3 = np.array([calc_roundness(s) for s in imgs3])
fig, ax = plt.subplots(2, 2, figsize=(10, 10), subplot_kw=({"xticks":(), "yticks":()}))
ax[0][0].imshow(imgs1[0]);
ax[0][1].imshow(imgs2[0]);
ax[1][0].imshow(imgs3[0]);
ax[1][1].plot(rgb_mean1[:,0], roundness1, 'o', color='red')
ax[1][1].plot(rgb_mean2[:,0], roundness2, 'o', color='yellow')
ax[1][1].plot(rgb_mean3[:,0], roundness3, 'o', color='orange')
ax[1][1].plot(rgb_mean1[:,0].mean(), roundness1.mean(), 'x', color='blue');
ax[1][1].plot(rgb_mean2[:,0].mean(), roundness2.mean(), 'x', color='blue');
ax[1][1].plot(rgb_mean3[:,0].mean(), roundness3.mean(), 'x', color='blue');
ax[1][1].set_xlabel("Red");
ax[1][1].set_ylabel("Roundness");
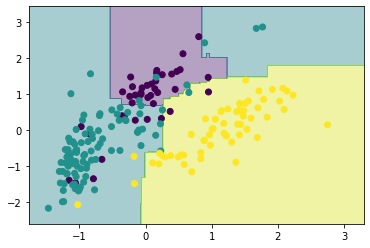
プロトタイプ法による識別
分類結果を表示する関数を定義します。
def show_result(X, y, model):
xrange = np.arange(X[:,0].min()*1.2,X[:,0].max()*1.2,0.01)
yrange = np.arange(X[:,1].min()*1.2,X[:,1].max()*1.2,0.01)
xx, yy = np.meshgrid(xrange, yrange)
result = model.predict(np.array([xx.reshape(-1),yy.reshape(-1)]).T).reshape(len(yrange), len(xrange))
plt.contourf(xx,yy,result, alpha=.4)
plt.scatter(X_scaled[:,0], X_scaled[:,1], c=y)
こちらの3種類の画像群を使用します。
rgb_mean1 = np.array([mean_col(s) for s in imgs1])
rgb_mean2 = np.array([mean_col(s) for s in imgs2])
rgb_mean3 = np.array([mean_col(s) for s in imgs3])
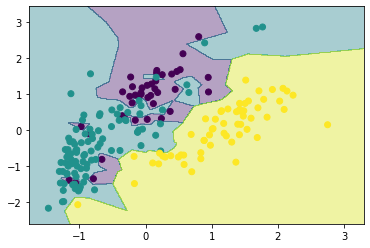
K近傍法により対象画像に元も近いデータの分類ラベルを予測値とします。
これ以降は使用する特徴量は画像全体のRGB各色の平均値となります。
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
import pandas as pd
X = pd.DataFrame({'Red':np.concatenate([rgb_mean1[:,0],rgb_mean2[:,0],rgb_mean3[:,0]]),
'Blue':np.concatenate([rgb_mean1[:,1],rgb_mean2[:,1],rgb_mean3[:,1]])})
y = np.array([0]*len(rgb_mean1)+[1]*len(rgb_mean2)+[2]*len(rgb_mean3))
# 標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# K近傍法
neighbor = KNeighborsClassifier(1)
neighbor.fit(X_scaled, y)
show_result(X_scaled, y, neighbor)
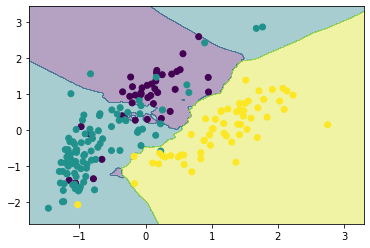
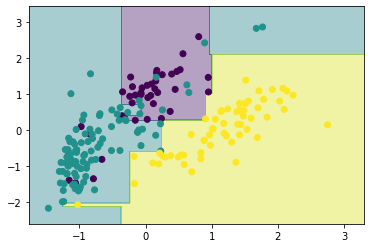
クラスの分布を考慮した識別
平均値までのユークリッド距離が同じでも、広く分布しているクラスに識別したほうが誤りが少なくなることが直感的にわかります。
たとえば、学習用の入力画像群の分布に基づいたマハラノビス距離により識別を行うことがあります。
まず、入力画像群の分布から、平均値と分散・共分散行列を求めます。
ここで、クラス$c$に属し、$K$次元の$N^{(c)}$個の学習用入力画像群を
\boldsymbol{x}_n^{(c)}=(x_{n1},x_{n2},\cdots,x_{nK})^T,\ n=1,\cdots,N^{(c)}
とすると、クラスの平均ベクトル $\boldsymbol{M}^{(c)}$と分散共分散行列$\boldsymbol{S}^{(c)}$は次のようになります。
\boldsymbol{M}^{(c)}=(M_1^{(c)},M_2^{(c)},\cdots,M_K^{(c)})^T
ただし、
M_i^{(c)}=\frac{1}{N^{(c)}}\sum_{n=1}^{N^{(c)}}x_{ni}
\boldsymbol{S}^{(c)}=
\left(
\begin{array}{ccc}
S_{11}^{(c)} & S_{12}^{(c)} & \cdots & S_{1K}^{(c)} \\
S_{21}^{(c)} & S_{22}^{(c)} & \cdots & S_{2K}^{(c)} \\
\vdots & \vdots & & \vdots \\
S_{K1}^{(c)} & S_{K2}^{(c)} & \cdots & S_{KK}^{(c)}
\end{array}
\right)
ただし、
S_{ij}^{(c)}=\frac{1}{N^{(c)}}\sum_{n=1}^{N^{(c)}}(x_{ni}-M_i^{(c)})(x_{nj}-M_j^{(c)})
各クラスの平均ベクトル$\boldsymbol{M}^{(c)}$をプロトタイプとしたとき、テスト画像$\boldsymbol{x}$から各プロトタイプへのユークリッド距離の2乗は、
d_e^{(c)}(\boldsymbol{x})=(\boldsymbol{x}-\boldsymbol{M}^{(c)})^T(\boldsymbol{x}-\boldsymbol{M}^{(c)})
マハラノビス距離は、
d_m^{(c)}(\boldsymbol{x})=(\boldsymbol{x}-\boldsymbol{M}^{(c)})^T(\boldsymbol{S}^{(c)})^{-1}(\boldsymbol{x}-\boldsymbol{M}^{(c)})
となります。
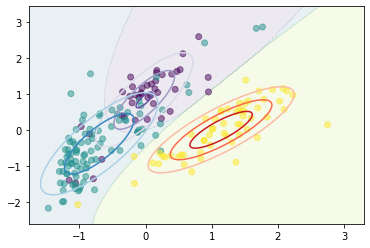
マハラノビス距離は、平均値までの距離が同じでも広がりの大きい分布に対して短くなる距離です。
ここで定義に従い計算と可視化を行います。
マハラノビス距離にしたとき最も近いデータのラベルを予測値とします。
from scipy.stats import multivariate_normal
X1 = X_scaled[:len(rgb_mean1),:]
X2 = X_scaled[len(rgb_mean1):(len(rgb_mean1)+len(rgb_mean2)),:]
X3 = X_scaled[(len(rgb_mean1)+len(rgb_mean2)):,:]
# 平均ベクトル
M1 = X1.mean(axis=0)
M2 = X2.mean(axis=0)
M3 = X3.mean(axis=0)
# 分散共分散行列
S1 = (X1-M1).T@(X1-M1) / len(X1)
S2 = (X2-M2).T@(X2-M2) / len(X2)
S3 = (X3-M3).T@(X3-M3) / len(X3)
# ラベル
labels=y
# 色の設定
cmaps = ['Purples', 'Blues', 'Reds', 'Greens']
xrange = np.arange(X_scaled[:,0].min()*1.2,X_scaled[:,0].max()*1.2,0.01)
yrange = np.arange(X_scaled[:,1].min()*1.2,X_scaled[:,1].max()*1.2,0.01)
xx, yy = np.meshgrid(xrange, yrange)
xy_sample = np.vstack([xx.ravel(), yy.ravel()]).T
# 各ガウス分布における等高線の表示
mp = np.zeros((len(yrange),len(xrange),3))
for i, (m, c) in enumerate(zip([M1,M2,M3], [S1,S2,S3])):
mp[:,:,i] = multivariate_normal(m, c).pdf(xy_sample).reshape(len(yrange),len(xrange))
plt.contour(xx, yy, mp[:,:,i], levels=3, cmap=cmaps[i])
# マハラノビス距離が大きいインデックスを分類結果とする
plt.contourf(xx, yy, mp.argmax(axis=2), levels=3, alpha=.1)
plt.scatter(X_scaled[:,0], X_scaled[:,1], c=y, alpha=.5)
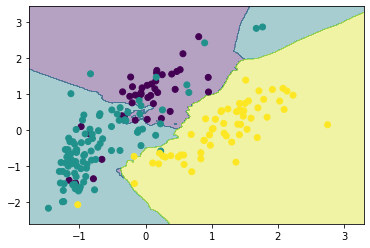
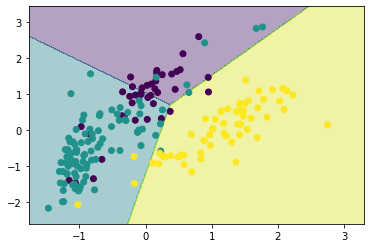
NN法とkNN法
NN法とは、ニアレストネイバーの略で最近傍の意味であり、テストデータに対して最も近傍の登録データを検索し、そのデータが属するクラスにテストデータを識別する。
テストデータの近傍の$k$個の登録データを検索し、帰属するサンプル数が最も多いクラスへテストデータを識別する方法がkNN法である。
neighbor = KNeighborsClassifier(6)
neighbor.fit(X_scaled, y)
show_result(X_scaled, y, neighbor)
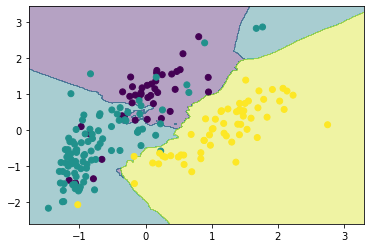
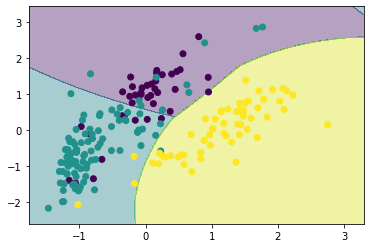
kd-tree法
NN法は、最近傍探索を行う際にテストデータとすべての登録データの距離を計算するため、計算時間を要するという問題があります。
そこで、木構造を用いて高速な最近傍探索を実現するkd-tree法が利用されています。
多次元の特徴空間にある$N$個のデータの集合$\boldsymbol{P}={p_1,p_2,\cdots,p_N}$を2分木により分割し、末端ノードにデータを格納します。
作成した2分木にテストデータを入力してトラバーサルすることにより最近傍探索を実現します。
kd-tree法による木の構築方法は次のようになります。
- 分割する特徴次元を選択する
- 選択した特徴次元において、中央値となる登録データを選択する。そのデータを通過し、座標軸に直交する超平面を用いて分割する。
- 超平面により、分割したデータを左右の子ノードに保存する。
- 子ノードにおいても1~3の処理を繰り返す。
KNeighborsClassifierのalgorithmをkd_treeと指定してクラスタリングを行います。
neighbor = KNeighborsClassifier(6, algorithm='kd_tree')
neighbor.fit(X_scaled, y)
show_result(X_scaled, y, neighbor)
scikit-learnのKDTreeを使用すると次のようになります。
from sklearn.neighbors import KDTree
import scipy.stats as stats
tree = KDTree(X_scaled, leaf_size=3)
dist, ind = tree.query(np.array([xx.reshape(-1),yy.reshape(-1)]).T, k=5)
result = np.array([stats.mode([y[i] for i in idx])[0][0] for idx in ind]).reshape(len(yrange), len(xrange))
plt.contourf(xx,yy,result, alpha=.4)
plt.scatter(X_scaled[:,0], X_scaled[:,1], c=y)
線形判別分析
線形判別分析は、クラス間をよく識別する特徴を選択する手法です。
クラス間を離し、クラス内の入力画像を集める評価基準で規定を求めます。
クラス$c$のパターン数を$N^{(c)}$、平均値を$\boldsymbol{M}^{(c)}$とし、全サンプル数を$N$、その平均ベクトルを$\boldsymbol{M}$としたとき、全サンプルの分散共分散行列$\boldsymbol{S}$は以下のようになります。
\boldsymbol{S}=\frac{1}{N}\sum_{n=1}^{N}(\boldsymbol{x}_{n}-\boldsymbol{M})(\boldsymbol{x}_{n}-\boldsymbol{M})^T
クラス$c$の分散共分散行列$\boldsymbol{S}^{(c)}$は、以下のようになります。
\boldsymbol{S}^{(c)}=\frac{1}{N}\sum_{n=1}^{N^{(c)}}(\boldsymbol{x}_{n}-\boldsymbol{M}^{(c)})(\boldsymbol{x}_{n}-\boldsymbol{M}^{(c)})^T
クラス内分散共分散行列$\boldsymbol{S}_w$とそのクラス間分散共分散行列$\boldsymbol{S}_b$は、次のようになります。
\boldsymbol{S}_w=\frac{1}{N}\sum_{c}N^{(c)}\boldsymbol{S}^{(c)}\\
\boldsymbol{S}_b=\frac{1}{N}\sum_{c}N^{(c)}(\boldsymbol{M}^{(c)}-\boldsymbol{M})(\boldsymbol{M}^{(c)}-\boldsymbol{M})^T\\
\boldsymbol{S}=\boldsymbol{S}_w+\boldsymbol{S}_b
クラス間の分離度を大きくするような$d$個の基底を求める問題は、以下の$\boldsymbol{S}_b\boldsymbol{S}_w^{-1}$の固有ベクトルを求める問題と同じになります。
\boldsymbol{S}_b\boldsymbol{S}_w^{-1}\boldsymbol{u}_j=\lambda_j\boldsymbol{u}_j
LDAの実行例を示します。
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X = pd.DataFrame({'Red':np.concatenate([rgb_mean1[:,0],rgb_mean2[:,0],rgb_mean3[:,0]]),
'Blue':np.concatenate([rgb_mean1[:,1],rgb_mean2[:,1],rgb_mean3[:,1]]),
'Green':np.concatenate([rgb_mean1[:,2],rgb_mean2[:,2],rgb_mean3[:,2]])})
y = np.array([0]*len(rgb_mean1)+[1]*len(rgb_mean2)+[2]*len(rgb_mean3))
# 標準化を行う
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# LDA
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit(X_scaled, y).transform(X_scaled)
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
for i in range(3):
ax[0].plot(X_scaled[y==i,0], X_scaled[y==i,1], 'o')
ax[1].plot(X_lda[y==i,0], X_lda[y==i,1], 'o')
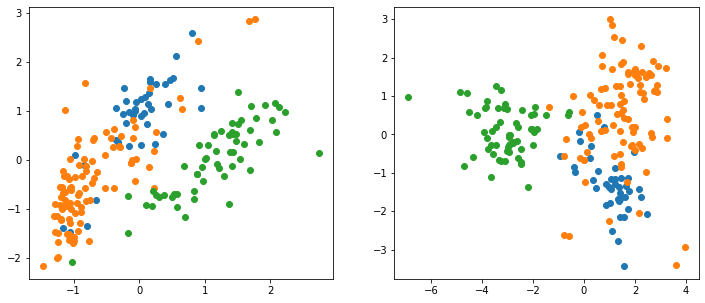
左側が実行前で右側が実行後です。
(ここでは大きく違いがみられませんでした。)
部分空間法
特徴空間の変換そのものを利用して識別する部分空間法を説明します。
SELFIC法
学習用の入力画像数に比べて特徴の数が多いと、特徴空間が広すぎ、真のクラスのまとまりが正確に推定できず、識別能力が劣化することがあります。
そのときには、主成分分析を用いて少数の特徴量にし、識別に不要な特徴を取り除いて、テスト画像への識別能力を上げることができる場合があります。
このように低次元にした特徴空間で、プロトタイプとの距離やマハラノビス距離などのクラスの近さに基づく識別方法をSELFIC法と呼びます。
主成分分析を行い、低次元空間へと変換(といっても3次元から2次元です。)します。
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit(X_scaled).transform(X_scaled)
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
for i in range(3):
ax[0].plot(X_scaled[y==i,0], X_scaled[y==i,1], 'o')
ax[1].plot(X_pca[y==i,0], X_pca[y==i,1], 'o')
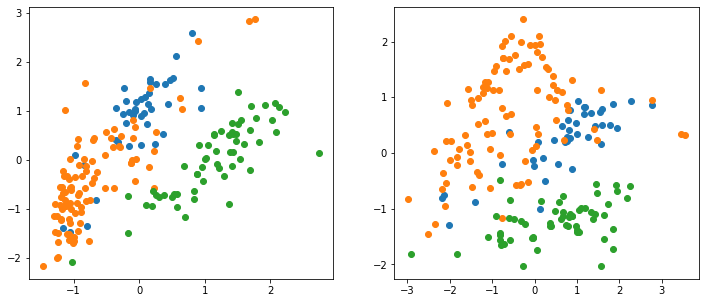
左の図が元の分布、右側が主成分分析後の空間となります。
これを利用して前に説明した識別などを行います。
機械学習の概要
教師なし学習
教師なし学習は、学習データのみからデータの性質を理解することであり、クラスタリングや次元圧縮に用いられます。
クラスタリングは、学習データに内在するクラスタを見つけ出す問題である。次元圧縮は、学習データの多次元情報を、その意味を保ちつつ、より少ない次元の情報に削減する問題であり、データの圧縮や可視化に用いられます。
教師あり学習
教師あり学習は、学習データとその正解情報からモデルを学習して未知の情報を予測することであり、クラス分類と回帰問題の2つの問題設定を行う。クラス分類は、学習データを入力し、その学習データが属するクラスラベルを出力するように識別モデルを構築して、未知データが属するクラスを求める問題である。回帰問題は、学習データを入力し、その学習データの出力である実数値を出力するように回帰モデルを構築し、未知データの情報を予測する問題です。
教師なし学習とクラスタリング
教師なし学習は、学習データのみからデータの性質を理解することです。
k-means法によるクラスタリング
ある特徴空間のなかでクラスごとに識別対象の入力画像が集まって存在することを仮定して、クラスごとに属する画像を同時に求めます。
この処理をクラスタリングと呼びます。
k-means法は、入力画像を分割するクラス数をあらかじめ$k$個と設定して分割し、これを初期状態として分割を繰り返し修正することで、よりよい分割を探し出す方法です。
from sklearn.cluster import KMeans
X = pd.DataFrame({'Red':np.concatenate([rgb_mean1[:,0],rgb_mean2[:,0],rgb_mean3[:,0]]),
'Blue':np.concatenate([rgb_mean1[:,1],rgb_mean2[:,1],rgb_mean3[:,1]])})
y = np.array([0]*len(rgb_mean1)+[1]*len(rgb_mean2)+[2]*len(rgb_mean3))
# 標準化を行う
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# k-means
km = KMeans(n_clusters=3)
km.fit(X_scaled, y)
show_result(X_scaled, y, km)
主成分分析による次元圧縮
主成分分析は、多次元の特徴空間に分散する多数の学習用入力画像から、分布をよく表現できる低次元の特徴空間を求める手法です。
この低次元の特徴空間を部分空間と呼びます。
ここで、$N$個の学習用の入力画像群の特徴量を$K$個とすると、入力画像は、特徴ベクトル
\boldsymbol{x}_n=(x_{n1},x_{n2},\cdots,x_{nK})^T,n=1,\cdots,N
となる。その平均ベクトル$\boldsymbol{M}$と分散共分散行列$\boldsymbol{S}$を以下により求めます。
\boldsymbol{M}=\frac{1}{N}\sum_{n=1}^N\boldsymbol{x}_n\\
\boldsymbol{S}=\frac{1}{N}\sum_{n=1}^N(\boldsymbol{x}_n-\boldsymbol{M})(\boldsymbol{x}_n-\boldsymbol{M})^T
主成分分析では、入力画像の特徴空間での分布において、平均値となる点を通り、広がりの最も大きい方向の直線である第1主成分を求めます。
次に、その第1主成分に直交しかつ平均を通る2番目に広がりの大きい方向の第2主成分の直線を求めます。
これは、分散共分散行列を用いて
\boldsymbol{S}\boldsymbol{u}_j=\lambda_j\boldsymbol{u}_j
を満たす固有値$\lambda_j$と固有ベクトル$\boldsymbol{u}_j$を求めます。
固有値$\lambda_j$の大きい方からそれに対応する固有ベクトル$\boldsymbol{u}_j$を$d$個選ぶと$d$次元の主成分が求まる。
顔の画像で主成分分析を行ってみる。平均画像と5つの主成分を画像化したものは次のようになります。
平均画像が少し怖くなってしまいました。苦手な方はすみません。
# 平均画像
plt.imshow(X.mean(axis=0), 'gray')
主成分画像は次のようになります。
X = np.concatenate([face1, face2, face3, face4, face5])
X_flat = X.flatten().reshape(len(X),64**2)/255.
y = np.array([0]*len(face1)+[1]*len(face2)+[2]*len(face3)+[3]*len(face4)+[4]*len(face5))
pca = PCA(n_components=50, whiten=True).fit(X_flat)
X_pca = pca.transform(X_flat)
# 主成分画像
fix, axes = plt.subplots(3, 5, figsize=(15, 8), subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(pca.components_[:15], axes.ravel())):
ax.imshow(component.reshape(64,64), cmap='gray')
ax.set_title("{}. component".format((i+1)))
教師あり学習
アダブースト
複数の識別器を組み合わせて1つの強力な識別器を学習するアンサンブル学習の1つとして、アダブーストがあります。
アダブーストは、2クラス分類問題に対して、逐次的に学習サンプルの重みを更新しながら識別器を選択することを繰り返し、最終的な識別関数を学習します。個々の識別器を弱識別器と呼び、それらを組み合わせた識別器を強識別器と呼びます。
まず、学習サンプルに対して均一の重みを与える。学習が始まり、1つの弱識別器が選択されると、正しく識別できるサンプルは重みが小さく、誤識別したサンプルの重みは大きくなる。次の弱識別器の学習では、学習サンプルの重みを考慮して、誤識別した学習サンプルを正しく識別する弱識別器が選択されます。
この処理を繰りかえして複数の弱識別器が選択されます。
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
ada = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), learning_rate=0.002, n_estimators=200)
ada.fit(X_scaled, y)
show_result(X_scaled, y, ada)
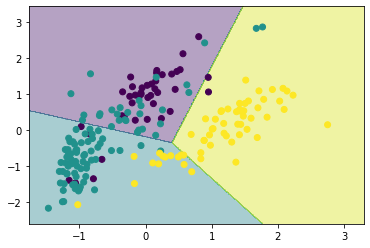
サポートベクタマシン
汎化能力の高い統計的学習手法の1つに、サポートベクターマシン(SVM) があります。
SVMでは、2クラスの分布を分ける超平面を決める際に、マージン最大化という考え方を導入しているため、高い識別性能をもちます。
ハードマージンSVM
ハードマージンSVMの線形識別器の識別関数$f(\boldsymbol{x})$は、以下のように表すことができます。
f(\boldsymbol{x})=sgn(\boldsymbol{w}^T\boldsymbol{x}+b)
$\boldsymbol{x}\in R^d$は$d$次元の特徴量、$\boldsymbol{w}\in R^d$は重みベクトル、$b\in R^d$はバイアス項であります。
識別関数$f(\boldsymbol{x})$は、特徴量と重みベクトルの内積にバイアス項を加えた値が0よりも大きい場合に1、小さい場合に-1を出力する。つまり、特徴空間を超平面により2つに分けることを表します。
学習ではマージン$d$を最大とするような超平面の重みベクトル$\boldsymbol{w}$とバイアス項$b$を求めることになります。
ソフトマージンSVM
ハードマージンSVMは、学習サンプルの線形分離が可能であることを仮定しています。
しかし、すべての問題において線形分離ができるわけではありません。
そのような場合、ある程度の誤差を許容して超平面を決定する手法として、ソフトマージンの概念を導入したソフトマージンSVMを適用します。
ソフトマージンSVMでは、ハードマージンSVMの目的関数にスラック変数$\xi_i$をペナルティ港として付き加えて、最小化を行います。
from sklearn.svm import LinearSVC
svc = LinearSVC(C=0.01)
svc.fit(X_scaled, y)
show_result(X_scaled, y, svc)
カーネルトリック
特徴量を非線形写像により高次元空間に写像し、高次元空間において線形分離可能な超平面を決定することを考えます。
こうして求められた超平面は非線形な境界線となるが、計算量が爆発的に増えます。
この計算量の問題を防ぐテクニックとしてカーネルトリックがあります。
カーネル関数を計算するのみで非線形な識別器の学習が可能となります。
from sklearn.svm import SVC
svm = SVC(kernel='rbf', C=0.5, gamma=0.1)
svm.fit(X_scaled, y)
show_result(X_scaled, y, svm)
ランダムフォレスト
ランダムフォレストとは、複数の決定木構造を持った多クラス識別器を構築するアンサンブル学習アルゴリズムであります。
ランダムフォレストは、学習サンプルをランダムサンプリングにより作成したサブセットごとに決定木を構築し、複数の決定木の結果を統合して識別します。
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=50, max_features=2, max_leaf_nodes=6)
rf.fit(X_scaled, y)
show_result(X_scaled, y, rf)
機械学習による画像認識の応用例
物体検出
物体検出とは、あるカテゴリに属する物体が画像中のどこに存在するかを求める問題です。
顔検出や人検出などの物体検出法では、検出ウィンドウのラスタスキャンにより、検出対象の位置を検出します。
カメラと検出対象の物体の距離に応じて画像中の検出対象物体の大きさが変化するため、同一サイズのウィンドウでは異なる大きさの物体を検出することはできない。そこで、入力画像からイメージピラミッドを作成し、各解像度の画像に対して検出ウィンドウをラスタスキャンすることで、マルチスケールの物体検出を実現します。
顔検出と顔識別
顔画像の特徴を捉える特徴量として、明暗差に着目したHaar-like特徴量が用いられています。
Haar-like特徴量は、以下に示すように、2つの矩形領域の平均輝度の差を特徴量とします。
H(r1,r2)=S(r1)-S(r2)
ここで、$S(r)$は領域$r$の平均輝度を算出する関数です。
face_cascade = cv2.CascadeClassifier('Lib/site-packages/cv2/data/haarcascade_frontalface_alt.xml')
# イメージファイルの読み込み
def detect_face(img):
img = img.copy()
# 顔を検知
faces = face_cascade.detectMultiScale(img)
for (x,y,w,h) in faces:
# 検知した顔を矩形で囲む
cv2.rectangle(img, (x,y), (x+w,y+h), (255,0,0), 2)
return img
plt.imshow(detect_face(img_demo))
plt.xticks([]);
plt.yticks([]);
人検出
人検出では、情報をヒストグラム化したHOG特徴量が利用されています。
HOG特徴量を画像から求め、画像をセルと呼ばれる矩形に分割し、セルごとに勾配方向ヒストグラム$h(\theta')$を作成します。
最後に複数のセルで構成されるブロックを用いて、勾配ヒストグラムを正規化します。
そして学習サンプルからHOG特徴量を抽出したら、SVMによる識別器の学習を行います。
fig, ax = plt.subplots(1, 2, figsize=(16, 5), subplot_kw={'xticks': (), 'yticks': ()})
for i in range(2):
img = img_demo2.copy()
if i == 0:
hog = cv2.HOGDescriptor()
hog.setSVMDetector(cv2.HOGDescriptor_getDefaultPeopleDetector())
else:
hog = cv2.HOGDescriptor((48,96), (16,16), (8,8), (8,8), 9)
hog.setSVMDetector(cv2.HOGDescriptor_getDaimlerPeopleDetector())
hogParams = {'winStride': (8, 8), 'padding': (4, 4), 'scale': 1.05}
human, r = hog.detectMultiScale(img, **hogParams)
for (x, y, w, h) in human:
cv2.rectangle(img, (x, y),(x+w, y+h),(0,50,255), 4)
ax[i].imshow(img);
類似画像検索
画像検索とは、入力画像を画像データベースと照合し、画像内の物体情報を探し出すことです。
このような画像検索には BoVW(Bag of Visual Words) という画像特徴表現と最近傍探索により実現できます。
BoVW表現とは、SIFTなどの特徴ベクトルをk-means法によりクラスタリングする。そして、各クラス中心をvisual wordsとして辞書を作成する。入力画像から抽出した局所特徴からvisual wordsごとの出現頻度をヒストグラムで表現するアプローチがBoVWです。
まず、各画像の局所特徴量をクラスタリングしてクラスタを作成します。
# BoVW表現の計算
# k=5の最近傍法
k = 5
detector = cv2.KAZE_create()
bowTrainer = cv2.BOWKMeansTrainer(k)
for file in X_train:
image = file.copy()
if image is not None:
_, descriptors = detector.detectAndCompute(image, None)
if descriptors is not None:
bowTrainer.add(descriptors.astype(np.float32))
# 各クラスタの中心
centroids = bowTrainer.cluster()
次に各画像に対して各クラスタの出現頻度のヒストグラムを求めます。
# 各局所特徴量の出現頻度のヒストグラムの計算(train)
matcher = cv2.BFMatcher()
extractor = cv2.BOWImgDescriptorExtractor(detector, matcher)
extractor.setVocabulary(centroids)
probs_train = []
for file in X_train:
descriptor = None
image = file.copy()
if image is not None:
keypoints = detector.detect(image, None)
if keypoints is not None:
descriptor = extractor.compute(image, keypoints)[0]
probs_train.append(descriptor)
# 各局所特徴量の出現頻度のヒストグラムの計算(test)
matcher = cv2.BFMatcher()
extractor = cv2.BOWImgDescriptorExtractor(detector, matcher)
extractor.setVocabulary(centroids)
probs_test = []
for file in X_test:
descriptor = None
image = file.copy()
if image is not None:
keypoints = detector.detect(image, None)
if keypoints is not None:
descriptor = extractor.compute(image, keypoints)[0]
probs_test.append(descriptor)
各画像のヒストグラムを比較して類似度を求めます。
# ヒストグラムの比較を行い類似度を計算する
prob = np.zeros([len(probs_test), len(probs_train)])
rank = []
for i, p1 in enumerate(probs_test):
tmp = []
for j, p2 in enumerate(probs_train):
#tmp.append([j,sum(map(lambda x: min(x[0], x[1]), zip(p1, p2)))])
tmp.append([j,cv2.compareHist(p1, p2, 0)])
rank.append(sorted(tmp, key = lambda x: -x[1])[:10])
rank = np.array(rank)
各画像に対して類似度の高いものを表示して結果を確認します。
今回はあまりうまく計算できていないようです。
# 類似度の近いものを表示
fig, ax = plt.subplots(5, 6, figsize=(18, 18), subplot_kw={'xticks': (), 'yticks': ()})
for i in range(25):
ax[i//5][0].imshow(X_test[int(i//5*10)])
ax[i//5][i%5+1].imshow(X_train[int(rank[i//5*10,i%5,0])])
ax[i//5][i%5+1].set_title('prob:{}'.format(round(rank[i//5*10,i%5,1]*100, 2)))
ヒストグラムを用いて分類モデルの作成も行ってみます。
こちらもかなり精度が低いものとなりました。
# 局所特徴量の出現頻度を使って分類モデルの作成
svm = SVC(kernel='rbf', C=0.5, gamma=0.1)
svm.fit(probs_train, y_train)
svm.score(probs_test, y_test)
次回
深層学習による画像認識と生成
参考
ディジタル画像処理[改訂第二版] | ディジタル画像処理編集委員会 |本 | 通販 | Amazon