以下の参考書の演習問題を解いていきます。
問題文や概要は参考書を参考にしてください。
ただし、解答集などが見当たらなかったため私個人の見解となります。
素人データ分析者がなんとかしてひねり出した解答ですので参考にはならないかもしれません。もっと良い方法があればコメントいただければと思います。数式がかなり見辛かなっており申し訳ありません。
サポートページに質問コーナーがあるので、こちらで聞いた方が確実です。
1
第$j$成分について、
$$
\begin{align}
\frac{\partial}{\partial\beta_j}\sum_{i=1}^N(y_i-\sum_{k=1}^p\beta_kx_{i,k})^2&=-2\sum_{i=1}^Nx_{i,j}(y_i-\sum_{k=1}^p\beta_kx_{i,k})\
&=-2[x_{1,j},\cdots,x_{N,j}]
\begin{bmatrix}y_1-\sum_{k=1}^p\beta_kx_{1,k}\
\vdots\
y_N-\sum_{k=1}^p\beta_kx_{N,k}
\end{bmatrix}
\end{align}
$$
$X$は
X=\begin{bmatrix}
x_{1,1} & \cdots & x_{1,p}\\
\vdots & \ddots & \vdots\\
x_{N,1} & \cdots & x_{N,p}
\end{bmatrix}
であるので、
\begin{bmatrix}
\sum_{k=1}^p\beta_kx_{1,k}\\
\vdots\\
\sum_{k=1}^p\beta_kx_{N,k}
\end{bmatrix}=
\begin{bmatrix}
\beta_1x_{1,1}+\cdots+\beta_px_{1,p}\\
\vdots\\
\beta_1x_{N,1}+\cdots+\beta_px_{N,p}
\end{bmatrix}=
\begin{bmatrix}
x_{1,1} & \cdots & x_{1,p}\\
\vdots & \ddots & \vdots\\
x_{N,1} & \cdots & x_{N,p}
\end{bmatrix}
\begin{bmatrix}
\beta_1\\
\vdots\\
\beta_p
\end{bmatrix}=
X\beta
とかける。ここで、$\beta=[\beta_1,\cdots,\beta_p]^T$とおいた。
以上より第2の等号
$$
-2X^T(y-X\beta)
$$
を導くことができる。
前の結果を利用すると、
$$
\frac{\partial}{\partial\beta_j}\sum_{i=1}^N(y_i-\sum_{k=1}^p\beta_kx_{i,k})^2=-2X^T(y-X\beta)
$$
と書ける、これが$0$と等しいとおくと、
$$
y-X\beta=0
$$
$X^TX$が$N×N$行列となり、逆行列が計算できるようになるので、
$$
\hat{\beta}=(X^TX)^{-1}X^Ty
$$
と求めることができる。
def linear(X, y):
p = X.shape[1]
x_bar = np.mean(X, axis=0, keepdims=True)
X = X - x_bar
y_bar = np.mean(y)
y = y - y_bar
beta = np.linalg.inv(X.T@X)@X.T@y
beta0 = y_bar - x_bar@beta
return beta, beta0
linear(X,y)
(array([10.98067026, -6.08852939, 5.4803042 , 0.37704431, 5.50047122]),
array([489.64859697]))
2
(a)
$$
f(x)=x
$$
に対し、
$$
f(\alpha x+(1-\alpha)y)=\alpha x+(1-\alpha)y\
\alpha f(x)+(1-\alpha)f(y)=\alpha x+(1-\alpha)y
$$
となり、任意の$0\leq\alpha\leq 1$に対し等号が成立する。
微分可能であるから、$x=0$における劣微分は$\partial f(x_0)=1$となる。
(b)
$$
f(x)=|x|
$$
に対し、
$$
f(\alpha x+(1-\alpha)y)=|\alpha x+(1-\alpha)y|\
\alpha f(x)+(1-\alpha)f(y)=\alpha|x|+(1-\alpha)|y|
$$
第2式の2乗から第1式の2乗を引くと
$$
(\alpha|x|+(1-\alpha)|y|)^2-|\alpha x+(1-\alpha)y|^2\
=\big(\alpha^2x^2+2\alpha(1-\alpha)|xy|+(1-\alpha)^2y^2 \big)-\big(\alpha^2 x^2+2\alpha(1-\alpha)xy+(1-\alpha)^2y^2\big)\
=2\alpha(1-\alpha)(|xy|-xy)\geq0
$$
であるため凸である。$z$について
$$
|x|\geq |x_0|+z(x-x_0)
$$
が成り立ち、$x_0=0$の場合
$$
|x|\geq zx
$$
である。
$$
x^2-z^2x^2=x^2(1-z^2)\geq0
$$
$x^2\geq0$であるから、$(1-z^2)\geq0$となる。したがって、$x=0$における劣微分は
$$
-1\leq z\leq 1
$$
となる。
3
(a)
$g(x),h(x)$が凸であるとき、任意の$0<\alpha<1$に対して、
$$
g(\alpha x+(1-\alpha)y)\leq\alpha g(x)+(1-\alpha)g(y)\
h(\alpha x+(1-\alpha)y)\leq\alpha h(x)+(1-\alpha)h(y)
$$
である。このとき、
$$
gh(x)=\beta g(x)+\gamma h(x)
$$
とすると、
$$
gh(\alpha x+(1-\alpha)y)\
=\beta g(\alpha x+(1-\alpha)y)+\gamma h(\alpha x+(1-\alpha)y)\
\leq\alpha g(x)+(1-\alpha)g(y)+\alpha h(x)+(1-\alpha)h(y)\
=\alpha(g(x)+h(x))+(1-\alpha)(g(y)+h(y))\
=\alpha gh(x)+(1-\alpha)gh(y)
$$
となり、$gh(x)$も凸となる。
(b)
$x,y=0,1$とすると、
$$
f(\alpha\cdot 0+(1-\alpha)\cdot 1)=f((1-\alpha))=1
$$
また、
$$
\alpha f(0)+(1-\alpha)f(1)=1-\alpha<1
$$
であるから、
$$
f(\alpha\cdot x+(1-\alpha)\cdot y)>\alpha f(x)+(1-\alpha)f(y)
$$
となり、凸とならない。
(c)
(a)の結果より、第1項と第2項を別々に考えてどちらも凸であれば問題の関数も凸であると判定する。
まず、共通部分について判定を行う。
$$
g(\beta)=|y-X\beta|^2
$$
に対し、
$$
g(\alpha\beta_1+(1-\alpha)\beta_2)=|y-X(\alpha\beta_1+(1-\alpha)\beta_2)|^2\
=|y|^2+|X(\alpha\beta_1+(1-\alpha)\beta_2)|^2-2y^TX(\alpha\beta_1+(1-\alpha)\beta_2)\
=|y|^2+ \alpha^2|X\beta_1|^2+2\alpha(1-\alpha)\beta_1^T\beta_2|X|^2+ (1-\alpha)^2|X\beta_2|^2 -2y^TX(\alpha\beta_1+(1-\alpha)\beta_2)\
\alpha g(\beta_1)+(1-\alpha)g(\beta_2)=\alpha|y-X\beta_1|^2+(1-\alpha)|y-X\beta_2|^2\
=|y|^2-2\alpha y^TX\beta_1+\alpha|X\beta_1|^2-2(1-\alpha) y^TX\beta_2+(1-\alpha)|X\beta_2|^2
$$
第2式から第1式を引くと、
$$
\alpha|X\beta_1|^2+(1-\alpha)|X\beta_2|^2-(\alpha^2|X\beta_1|^2+2\alpha(1-\alpha)\beta_1^T\beta_2|X|^2+ (1-\alpha)^2|X\beta_2|^2)\
=(1-\alpha)\bigg(\alpha|X\beta_1|^2+(2-\alpha)|X\beta_2|^2-2\alpha\beta_1^T\beta_2|X|^2\bigg)\
=(1-\alpha)\bigg(|\alpha X\beta_1-X\beta_2|^2+\alpha(1-\alpha)|X\beta_1|^2+(1-\alpha)|X\beta_2|^2\bigg)\geq0
$$
となり、凸である。
したがって、以下の各$h(\beta)$が凸であるとき問題の関数も凸となる。
1
$h(\beta)=|\beta|_0,\beta_1,\beta_2=\boldsymbol{0},\boldsymbol{1}$とすると、
$$
h(\alpha\beta_1+(1-\alpha)\beta_2)=p
$$
また、
$$
\alpha h(\beta_1)+(1-\alpha)h(\beta_2)=\alpha p
$$
であるから、
$$
\alpha h(\beta_1)+(1-\alpha)h(\beta_2)\leq h(\alpha\beta_1+(1-\alpha)\beta_2)
$$
となり、凸とならない。
2
$h(\beta)=|\beta|_1$とすると、
$$
h(\alpha\beta_1+(1-\alpha)\beta_2)=|\alpha\beta_1+(1-\alpha)\beta_2|_1
$$
また、
$$
\alpha h(\beta_1)+(1-\alpha)h(\beta_2)=\alpha|\beta_1|_1+(1-\alpha)|\beta_2|_1
$$
であるから、第2式の2乗から第1式の2乗を引くと
$$
\alpha^2\beta_1^T\beta_1+2\alpha(1-\alpha)|\beta_1\beta_2|_1+(1-\alpha)^2\beta_2^T\beta_2-(\alpha\beta_1+(1-\alpha)\beta_2)^T(\alpha\beta_1+(1-\alpha)\beta_2)\
=2\alpha(1-\alpha)(|\beta_1\beta_2|_1-\beta_1^T\beta_2)\geq0
$$
となり、凸となる。
3
$h(\beta)=|\beta|_2$とすると、
$$
h(\alpha\beta_1+(1-\alpha)\beta_2)=\sqrt{(\alpha\beta_1+(1-\alpha)\beta_2)^T(\alpha\beta_1+(1-\alpha)\beta_2)}
$$
また、
$$
\alpha h(\beta_1)+(1-\alpha)h(\beta_2)=\alpha\sqrt{\beta_1^T\beta_1}+(1-\alpha)\sqrt{\beta_2^T\beta_2}
$$
であるから、第2式の2乗から第1式の2乗を引くと
$$
\alpha^2\beta_1^T\beta_1+(1-\alpha)^2\beta_2^T\beta_2+2\alpha(1-\alpha)\sqrt{|\beta_1^T\beta_2|^2})-(\alpha^2\beta_1^T\beta_1+(1-\alpha)^2\beta_2^T\beta_2+2\alpha(1-\alpha)\beta_1^T\beta_2)\
=2\alpha(1-\alpha)(|\beta_1^T\beta_2|-\beta_1^T\beta_2)\geq0
$$
となり、凸となる。
4
(a)
$f$が凸であるから、
$$
f(\alpha x+(1-\alpha)x_0)\leq\alpha f(x)+(1-\alpha)f(x_0)\
\alpha f(x)\geq f(x_0+\alpha (x-x_0))-(1-\alpha)f(x_0)\
\alpha f(x)\geq \alpha f(x_0)+f(x_0+\alpha (x-x_0))-f(x_0)\
f(x) \geq f(x_0)+\frac{f(x_0+\alpha (x-x_0))-f(x_0)}{\alpha(x-x_0)}(x-x_0)
$$
$\alpha\rightarrow 0$の極限をとると、
$$
f(x)\geq f(x_0)+f'(x_0)(x-x_0)
$$
となる。
(b)
劣微分$\partial f(x_0)$は、
$$
f(x)\geq f(x_0)+z(x-x_0)
$$
であるような$z$の集合である。
$x>x_0$のとき、
$$
z\leq\frac{f(x)-f(x_0)}{x-x_0}
$$
$x<x_0$のとき、
$$
z\geq\frac{f(x)-f(x_0)}{x-x_0}
$$
$x_0$について極限を取ると
$$
\lim_{x\rightarrow x_0-0}\frac{f(x)-f(x_0)}{x-x_0}\leq z\leq \lim_{x\rightarrow x_0+0}\frac{f(x)-f(x_0)}{x-x_0}
$$
$f(x)$は$x_0$で微分可能であるから、$z$は微分係数と一致して${f'(x_0)}$となる。
5
(a)
$f(x)=|x|$の$x=0$における劣微分は$[-1,1]$であることを利用する。
f'(x)=\left\{\begin{array}{ll}
2x-2 & x>0\\
-3+[-1,1]=[-4,-2] & x=0\\
2x-1 & x<0
\end{array}\right.
$x\leq 0$において$f'(x)<0$であるから、$f'(x)=0$となるのは$x=1$である。
このとき極小値は、$f(1)=1-3+1=-1$である。
(b)
f'(x)=\left\{\begin{array}{ll}
2x+3 > 0 & x>0\\
2+[-1,1]=[-1,3] & x=0\\
2x-1<0 & x<0
\end{array}\right.
$f'(x)=0$となるのは$x=0$である。
このとき極小値は、$f(0)=0$である。
import numpy as np
import matplotlib.pyplot as plt
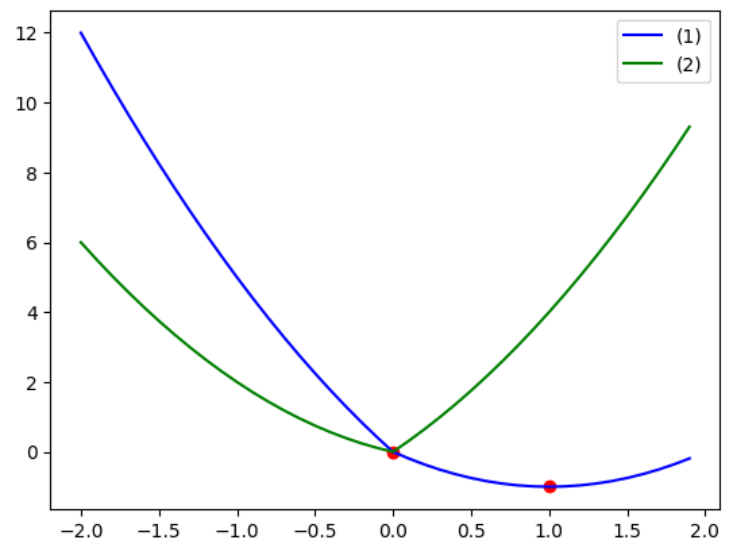
x = np.arange(-2,2,0.1)
func1 = lambda x: x**2-3*x+np.abs(x)
func2 = lambda x: x**2+x+2*np.abs(x)
plt.plot(x, func1(x), color='blue', label='(1)')
plt.scatter(1,-1, c='red')
plt.plot(x, func2(x), color='green', label='(2)')
plt.scatter(0,0, c='red')
plt.legend();
6
L=\frac{1}{2N}\sum_{i=1}^N(y_i-\sum_{j=1}^p\beta_jx_{i,j})^2+\lambda\sum_{j=1}^p|\beta_j|
について、
\begin{align}
\frac{\partial L}{\partial \beta_j}&=-\frac{1}{N}\sum_{i=1}^Nx_{i,j}(y_i-\sum_{k=1}^p\beta_kx_{i,k})+\lambda
\left\{\begin{array}{ll}
1&\beta_j>0\\
[-1,1]&\beta_j=0\\
-1&\beta_j<0
\end{array}\right.\\
&=-\sum_{i=1}^nx_{i,j}y_i+\frac{1}{N}\sum_{i=1}^N\sum_{k=1}^p \beta_kx_{i,j}x_{i,k}+\lambda
\left\{\begin{array}{ll}
1&\beta_j>0\\
[-1,1]&\beta_j=0\\
-1&\beta_j<0
\end{array}\right.\\
&=-s_j+
\left\{\begin{array}{ll}
\beta_j+\lambda&\beta_j>0\\
\lambda[-1,1]&\beta_j=0\\
\beta_j-\lambda&\beta_j<0
\end{array}\right.
\end{align}
$\beta_j>0$のとき、
-s_j+\beta_j+\lambda=0\\
\beta_j=s_j-\lambda\\
\beta_j>0\rightarrow s_j>\lambda
$\beta_j=0$のとき、
s_j=\lambda[-1,1]\\
-\lambda\leq s_j \leq \lambda
$\beta_j<0$のとき、
-s_j+\beta_j-\lambda=0\\
\beta_j=s_j+\lambda\\
\beta_j<0\rightarrow s_j<-\lambda
であるので、極小値となる$\beta_j$はまとめると
\beta_j=\left\{\begin{array}{ll}
s_j-\lambda & s_j>\lambda\\
0 & -\lambda\leq s_j \leq \lambda\\
s_j+\lambda & s_j<-\lambda
\end{array}\right.
7
\begin{align}
S_\lambda(x)&=\left\{\begin{array}{ll}
x-\lambda & x>\lambda\\
0 & |x| \leq \lambda\\
x+\lambda & x<-\lambda
\end{array}\right.\\
&=\left\{\begin{array}{ll}
|x|-\lambda & |x|>\lambda\\
0 & |x| \leq \lambda\\
-|x|+\lambda & -|x|<-\lambda
\end{array}\right.\\
&=\left\{\begin{array}{ll}
sign(x)(|x|-\lambda) & |x|-\lambda>0\\
0 & |x|-\lambda \leq 0
\end{array}\right.\\
\end{align}
となるので、
S_\lambda(x)=sign(x)(|x|-\lambda)_+
と書ける。
import numpy as np
import matplotlib.pyplot as plt
def bracket_plus(x):
x[x<=0] = 0
return x
def soft_th(lam, x):
return np.sign(x)*bracket_plus(np.abs(x)-lam)
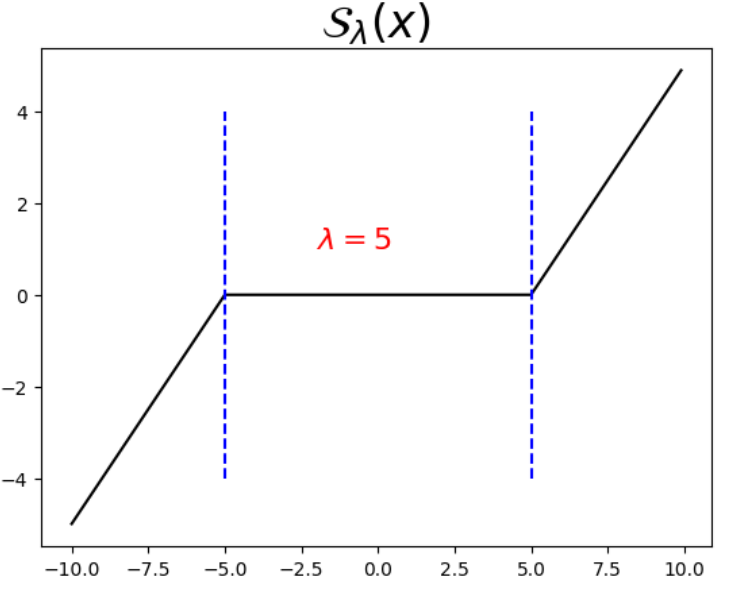
x = np.arange(-10, 10, 0.1)
y = soft_th(5, x)
plt.plot(x, y, c='black')
plt.title(r"${\cal S}_\lambda(x)$", size=24)
plt.plot([-5,-5],[-4,4],c='blue',linestyle='dashed')
plt.plot([5,5],[-4,4],c='blue',linestyle='dashed')
plt.text(-2, 1, r"$\lambda=5$", c="red", size=16)
8
def sort_th(lam, x):
return np.sign(x) * np.maximum(np.abs(x) - lam, np.zeros(1))
def centralize(X0, y0, standardize=True):
X = X0.copy()
y = y0.copy()
X_bar = np.mean(X, axis=0)
X_sd = np.std(X, axis=0)
y_bar = np.mean(y, axis=0)
X -= X_bar
if standardize:
X /= X_sd
y -= y_bar
return X,y,X_bar,X_sd,y_bar
def linear_lasso(X, y, lam=0, beta=None):
n, p = X.shape
if beta is None:
beta = np.zeros(p)
X, y, X_bar, X_sd, y_bar = centralize(X,y)
eps = 1
while eps > 1e-5:
beta_old = beta.copy()
for j in range(p):
index = np.ones(p, dtype='bool')
index[j] = False
r = y.ravel() - np.sum(X[:, index]*beta[index], axis=1, keepdims=True).ravel()
z = (r.T@X[:,j]/n) / (X[:,j].T@X[:,j]/n)
beta[j] = sort_th(lam, z)
eps = np.linalg.norm(beta - beta_old, 2)
beta = beta / X_sd
beta_0 = y_bar - X_bar@beta
return beta, beta_0
def setting_plot(xlim=None,ylim=None,xlabel=None,ylabel=None,title=None):
if xlim is not None:
plt.xlim(xlim)
if ylim is not None:
plt.ylim(ylim)
if xlabel is not None:
plt.xlabel(xlabel)
if ylabel is not None:
plt.ylabel(ylabel)
if title is not None:
plt.title(title)
df = np.loadtxt('crime.txt', delimiter='\t')
X = df[:, [i for i in range(2,7)]]
y = df[:,0]
n, p = X.shape
lambda_seq = [10, 50, 100]
r = len(lambda_seq)
coef_seq = np.array([linear_lasso(X, y, lmd)[0] for lmd in lambda_seq])
plt.plot(lambda_seq, coef_seq);
setting_plot(xlabel=r"$\lambda$",ylabel=r"$\beta$")
9
from sklearn.datasets import load_boston
boston = load_boston()
X = boston.data
y = boston.target
lambda_seq = np.arange(0.001,20,0.1)
coef_seq = np.array([linear_lasso(X, y, lmd)[0] for lmd in lambda_seq])
labels=boston.feature_names
plt.plot(np.log(lambda_seq), coef_seq, label=labels)
setting_plot(xlim=(-7,3), ylim=(-20,5),
xlabel=r"$\log\lambda$",ylabel=r"$\beta$")
plt.legend(loc="lower right");
10
すべての$\beta_j$に対し、$\beta_j=0$が成り立つことから、
\left\{\begin{array}{ll}
r_i=y_i\\
0 = S_\lambda\bigg(\frac{1}{n}\sum_{i=1}^nx_{i,j}r_i \bigg)
\end{array}\right.\\
\rightarrow S_\lambda\bigg(\frac{1}{n}\sum_{i=1}^nx_{i,j}y_i \bigg)=0
$S_\lambda(x)=0$のとき$|x|\leq\lambda$であるから、
\bigg|\frac{1}{n}\sum_{i=1}^nx_{i,j}y_i \bigg|\leq\lambda
$\lambda$が最小値となるのは等号が成立する場合であるが、
任意の$j$で成り立つためには左辺の$j$に関する最大値と等しくなる必要がある。
したがって、
\lambda=\max_{1\leq j \leq p}\bigg|\frac{1}{n}\sum_{i=1}^nx_{i,j}y_i \bigg|
となる。
11
$XX^T$の固有値が$\gamma_1,\cdots,\gamma_p$のとき、
$XX^T$に逆用列が存在しない場合、行列式が0となるので、
$$
|XX^T|=0
$$
となる。行列式は固有値の積に等しいから、
$$
\gamma_1\gamma_2\cdots\gamma_p=0
$$
である(少なくとも1つの固有値が0である場合)。
$XX^T+N\lambda I$の固有値を$t_1,\cdots,t_p$とする。
$$
|XX^T+N\lambda I-tI|=0\
|XX^T-(t-N\lambda) I|=0
$$
$XX^T$の固有値が$\gamma_1,\cdots,\gamma_p$であるから、
$$
t-N\lambda=\gamma_1,\cdots,\gamma_p\
t_1,\cdots,t_p = \gamma_1+N\lambda,\cdots,\gamma_p+N\lambda
$$
また、$XX^T$は非負定値であるので、その固有値は$\gamma_1,\cdots,\gamma_p\geq0$となる。
したがって、$\lambda>0$であるとき、
$$
\gamma_j+N\lambda>0
$$
となって、
$$
t_1,\cdots,t_p>0
\rightarrow t_1t_2\cdots t_p>0
$$
のように逆行列が存在する条件を満たす。
12
$\lambda\geq0$として、
L=\frac{1}{2N}\|y-X\beta\|_2^2+\frac{\lambda}{2}\|\beta\|_2^2=\frac{1}{2N}\sum_{i=1}^N(y_i-\beta_1x_{i,1}-\cdots-\beta_px_{i,p})^2+\frac{\lambda}{2}\sum_{j=1}^p\beta_j^2
を$\beta$で微分して0と等値とする。
\begin{align}
\frac{\partial L}{\partial \beta}&=-\frac{1}{N}X^T(y-X\beta)+\lambda I\beta\\
&=-\frac{1}{N}X^Ty+\frac{1}{N}(X^TX+N\lambda I)\beta=0
\end{align}
前問の結果より、$X^TX+N\lambda I$は逆行列をもつから、
(X^TX+N\lambda I)\beta =X^Ty\\
\beta = (X^TX+N\lambda I)^{-1}X^Ty
13
def ridge(X, y, lam=0):
n, p = X.shape
x_bar = np.mean(X, axis=0, keepdims=True)
X = X - x_bar
y_bar = np.mean(y)
y = y - y_bar
beta = np.linalg.inv(X.T@X+n*lam*np.eye(p))@X.T@y
beta0 = y_bar - x_bar@beta
return beta, beta0
df = np.loadtxt('crime.txt', delimiter='\t')
X = df[:, [i for i in range(2,7)]]
y = df[:,0]
linear(X, y)
(array([10.98067026, -6.08852939, 5.4803042 , 0.37704431, 5.50047122]),
array([489.64859697]))
ridge(X, y)
(array([10.98067026, -6.08852939, 5.4803042 , 0.37704431, 5.50047122]),
array([489.64859697]))
ridge(X, y, 200)
(array([ 5.32672839, -1.38451516, 1.43075509, -0.81986481, 0.09200358]),
array([599.44106767]))
14
df = np.loadtxt('crime.txt', delimiter='\t')
X = df[:, [i for i in range(2,7)]]
y = df[:,0]
p = X.shape[1]
lambda_seq = np.arange(0.1, 200, 0.1)
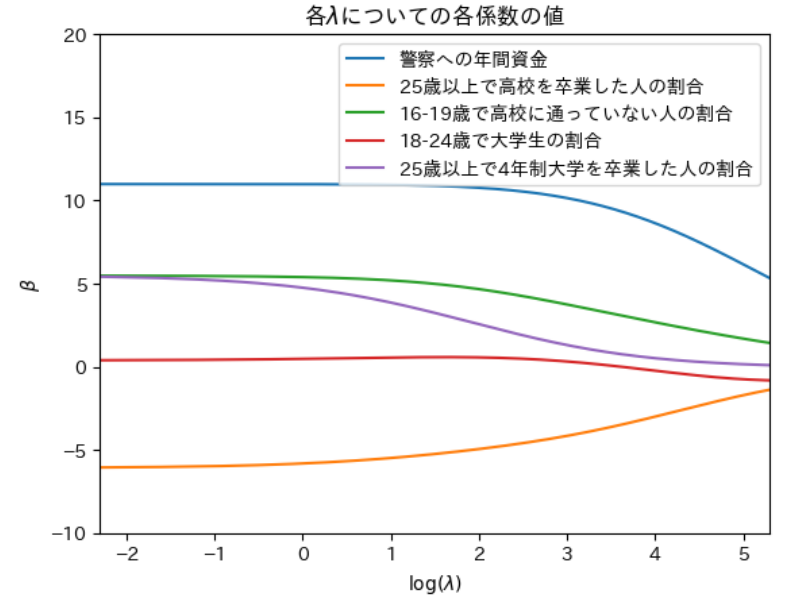
labels=['警察への年間資金', '25歳以上で高校を卒業した人の割合','16-19歳で高校に通っていない人の割合',
'18-24歳で大学生の割合', '25歳以上で4年制大学を卒業した人の割合']
coef_seq = np.array([ridge(X, y, lmd)[0] for lmd in lambda_seq])
plt.plot(np.log(lambda_seq), coef_seq, label=labels);
setting_plot(xlim=(np.log(0.1),np.log(200)), ylim=(-10,20),
xlabel=r"$\log(\lambda)$",ylabel=r"$\beta$",
title=r"各$\lambda$についての各係数の値")
plt.legend(loc='upper right')
15
(a)1
$x_{i,1},x_{i,2}\in,\mathbb{R}(i=1,\cdots,N)$が与えられてときに、
S=\sum_{i=1}^N(y_i-\beta_1x_{i,1}-\beta_2x_{i,2})^2
を最小にする$\beta_1,\beta_2$を$\hat{\beta}_1,\hat{\beta}_2$とおき、
\hat{\beta}_1x_{i,1}+\hat{\beta}_2x_{i,2}
を$\hat{y}_i$とおく($i=1,\cdots,N$)。
$S$を$\beta_1,\beta_2$で微分すると、
$$
\frac{\partial S}{\partial \beta_1}=2\sum_{i=1}^N(-x_{i,1})(y_i-\beta_1x_{i,1}-\beta_2x_{i,2})\
\frac{\partial S}{\partial \beta_2}=2\sum_{i=1}^N(-x_{i,2})(y_i-\beta_1x_{i,1}-\beta_2x_{i,2})
$$
であり、最小値を取るとき、
\beta_1=\hat{\beta}_1\\
\beta_2=\hat{\beta}_2
でそれぞれ0となる。したがって、
\sum_{i=1}^Nx_{i,1}(y_i-\hat{\beta}_1x_{i,1}-\hat{\beta}_2x_{i,2})=\sum_{i=1}^Nx_{i,1}(y_i-\hat{y})=0\\
\sum_{i=1}^Nx_{i,2}(y_i-\hat{\beta}_1x_{i,1}-\hat{\beta}_2x_{i,2})=\sum_{i=1}^Nx_{i,2}(y_i-\hat{y})=0
となる。
(a)2
任意の$\beta_1,\beta_2$について、
\begin{align}
y_i-\beta_1x_{i,1}-\beta_2x_{i,2}&=y_i-\hat{y}+\hat{y}-\beta_1x_{i,1}-\beta_2x_{i,2}\\
&=y_i-\hat{y}+(\hat{\beta}_1x_{i,1}+\hat{\beta}_2x_{i,2})-\beta_1x_{i,1}-\beta_2x_{i,2}\\
&=y_i-\hat{y}-(\beta_1-\hat{\beta}_1)x_{i,1}-(\beta_2-\hat{\beta}_2)x_{i,2}
\end{align}
と書ける。また、
\begin{align}
\sum_{i=1}^N(y_i-\beta_1x_{i,1}-\beta_2x_{i,2})^2&=\sum_{i=1}^N(y_i-\hat{y}-(\beta_1-\hat{\beta}_1)x_{i,1}-(\beta_2-\hat{\beta}_2)x_{i,2})^2\\
&=(\beta_1-\hat{\beta}_1)^2\sum_{i=1}^Nx_{i,1}^2+2(\beta_1-\hat{\beta}_1)(\beta_2-\hat{\beta}_2)\sum_{i=1}^Nx_{i,1}x_{i,2}+(\beta_2-\hat{\beta}_2)^2\sum_{i=1}^Nx_{i,2}^2+\sum_{i=1}^N(y_i-\hat{y})^2+\sum_{i=1}^Nx_{i,1}(y_i-\hat{y})+\sum_{i=1}^Nx_{i,2}(y_i-\hat{y})\\
&=(\beta_1-\hat{\beta}_1)^2\sum_{i=1}^Nx_{i,1}^2+2(\beta_1-\hat{\beta}_1)(\beta_2-\hat{\beta}_2)\sum_{i=1}^Nx_{i,1}x_{i,2}+(\beta_2-\hat{\beta}_2)^2\sum_{i=1}^Nx_{i,2}^2+\sum_{i=1}^N(y_i-\hat{y})^2
\end{align}
と書ける(前問までの結果を利用)。
(b)
$\sum_{i=1}^Nx_{i,1}^2=\sum_{i=1}^Nx_{i,2}^2=1,\sum_{i=1}^Nx_{i,1}x_{i,2}=0$の場合を考えると、最小化する式は
(\beta_1-\hat{\beta}_1)^2+(\beta_2-\hat{\beta}_2)^2+\sum_{i=1}^N(y_i-\hat{y})^2
ここで、$\hat{\beta}_1,\hat{\beta}_2$を中心とした円を考える。
$\beta_1,\beta_2$が$|\beta_1|+|\beta_2|=1$上にあるとする。ラグランジュの未定乗数法を用いて、
$$
L=(\beta_1-\hat{\beta}_1)^2+(\beta_2-\hat{\beta}_2)^2-2\lambda(|\beta_1|+|\beta_2|-1)
$$
とおく。ただし、$\lambda>0$とする。
\frac{\partial L}{\partial \beta_1}=2(\beta_1-\hat{\beta}_1)-\left\{\begin{array}{ll}
2\lambda<0&\beta_1>0\\
2\lambda[-1,1]&\beta_1=0\\
-2\lambda>0&\beta_1<0
\end{array}\right.\\
\frac{\partial L}{\partial \beta_2}=2(\beta_2-\hat{\beta}_2)-\left\{\begin{array}{ll}
2\lambda<0&\beta_2>0\\
2\lambda[-1,1]&\beta_2=0\\
-2\lambda>0&\beta_2<0
\end{array}\right.
$\beta_1=0$のとき
-\hat{\beta}_1-\lambda[-1,1]=0\\
-\lambda\leq\hat{\beta}_1\leq\lambda
$\beta_2=1$のとき、$\lambda=-1+\hat{\beta}_2$だから、
-(-1+\hat{\beta}_2)\leq\hat{\beta}_1\leq-1+\hat{\beta}_2
$\beta_2=-1$のとき、$\lambda=-1-\hat{\beta}_2$だから、
-(-1-\hat{\beta}_2)\leq\hat{\beta}_1\leq-1-\hat{\beta}_2
(c)
$\beta_1,\beta_2$が$\beta_1^2+\beta_2^2=1$上にある場合、ラグランジュの未定乗数法を用いて、
L_2=(\beta_1-\hat{\beta}_1)^2+(\beta_2-\hat{\beta}_2)^2-\lambda(\beta_1^2+\beta_2^2-1)
とおくと、これは微分可能であるので、
\frac{\partial L}{\partial \beta_1}=2(\beta_1-\hat{\beta}_1)-2\lambda\beta_1=0\\
\frac{\partial L}{\partial \beta_2}=2(\beta_2-\hat{\beta}_2)-2\lambda\beta_2=0
$\beta_1,\beta_2$について式変形して
\beta_1=\frac{\hat{\beta}_1}{1-\lambda}\\
\beta_2=\frac{\hat{\beta}_2}{1-\lambda}
\beta_1^2+\beta_2^2=1\\
\bigg(\frac{\hat{\beta}_1}{1-\lambda}\bigg)^2+\bigg(\frac{\hat{\beta}_2}{1-\lambda}\bigg)^2=1\\
1-2\lambda+\lambda^2=\hat{\beta}_1^2+\hat{\beta}_2^2\\
\lambda^2-2\lambda+1-\hat{\beta}_1^2-\hat{\beta}_2^2=0
この2次方程式を解くと、
\lambda=1±\sqrt{\hat{\beta}_1^2+\hat{\beta}_2^2}
\beta_1=±\frac{\hat{\beta}_1}{\sqrt{\hat{\beta}_1^2+\hat{\beta}_2^2}}\\
\beta_2=±\frac{\hat{\beta}_2}{\sqrt{\hat{\beta}_1^2+\hat{\beta}_2^2}}
$\hat{\beta}_1,\hat{\beta}_2$が円の外部にあるとすると、
\hat{\beta}_1^2+\hat{\beta}_2^2\geq1
$\beta_1=0$の場合、$\hat{\beta}_1=0$であり、
\hat{\beta}_2=±\sqrt{\hat{\beta}_1^2+\hat{\beta}_2^2}
\rightarrow \hat{\beta}_2\leq-1,\ 1\leq\hat{\beta}_2
$\beta_2=0$の場合、$\hat{\beta}_2=0$であり、
\hat{\beta}_1=±\sqrt{\hat{\beta}_1^2+\hat{\beta}_2^2}
\rightarrow \hat{\beta}_1\leq-1,\ 1\leq\hat{\beta}_1
となる。Lassoに比べ、$\hat{\beta}_1,\hat{\beta}_2$が0となる領域は狭くなる。
import numpy as np
import matplotlib.pyplot as plt
x=np.arange(-5,5,0.05)
y=np.arange(-5,5,0.05)
xx,yy=np.meshgrid(x,y)
xx = xx.ravel()
yy = yy.ravel()
area1 = (((xx<=(-1+yy))&((-(-1+yy))<=xx))|((xx<=-1-yy)&((-(-1-yy))<=xx))).reshape(len(x),len(y)).astype(int)
area2 = (((yy<=(-1+xx))&((-(-1+xx))<=yy))|((yy<=-1-xx)&((-(-1-xx))<=yy))).reshape(len(x),len(y)).astype(int)
plt.imshow(area1+area2, cmap='Greens');
plt.hlines(100,0,200,color='black')
plt.vlines(100,0,200,color='black')
plt.xlim(0,200)
plt.ylim(0,200)
plt.xticks(np.arange(0,200,20),np.round(x[::20],2));
plt.yticks(np.arange(0,200,20),np.round(x[::20],2));
16
Ridge回帰の目的関数
L=\frac{1}{N}\sum_{i=1}^N(y_i-\beta_0-\sum_{j=1}^px_{i,j}\beta_j)^2+\lambda\sum_{j=1}^p\beta_j^2
ここで任意の$i$について$x_{i,k}=x_{i,l}$であるとする。
$L$を$\beta_k,\beta_l$でそれぞれ微分して0と等値とする。
\frac{\partial L}{\partial\beta_k}=-\frac{2}{N}\sum_{i=1}^Nx_{i,k}(y_i-\beta_0-\sum_{j=1}^px_{i,j}\beta_j)+2\lambda\beta_k=0\\
\frac{\partial L}{\partial\beta_l}=-\frac{2}{N}\sum_{i=1}^Nx_{i,l}(y_i-\beta_0-\sum_{j=1}^px_{i,j}\beta_j)+2\lambda\beta_l=0
$x_{i,k}=x_{i,l}$であるため、$\beta_k,\beta_l$についてそれぞれ同じ方程式となる。
したがって、$\beta_k=\beta_l$となる。
17
n = 500
x = np.zeros((n, 6))
z = np.random.normal(size=(n,2))
x[:,:3] = z[:,[0]] + np.random.normal(size=(n,3)) / 5
x[:,3:] = z[:,[1]] + np.random.normal(size=(n,3)) / 5
y = 3*z[:,0] - 1.5*z[:,1] + 2*np.random.normal(size=(n))
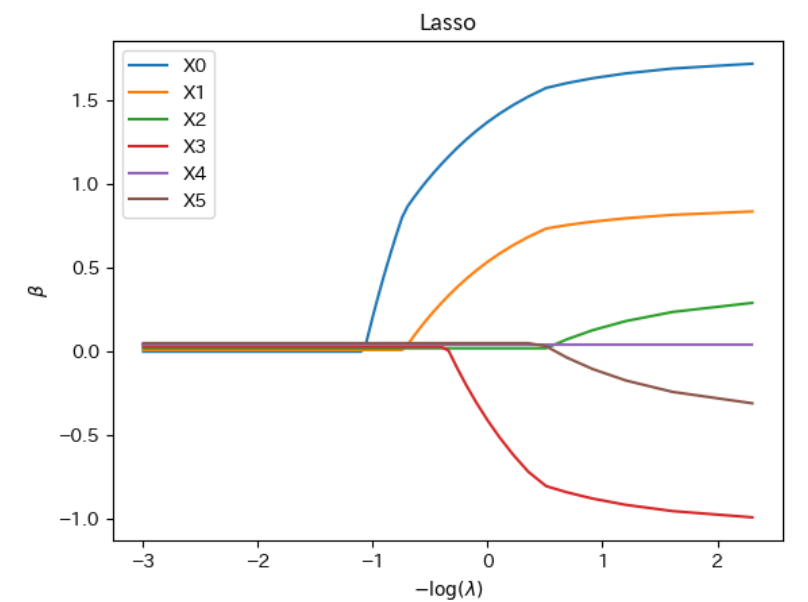
lambda_seq = np.arange(0.1, 20, 0.1)
coef_seq = np.array([linear_lasso(x, y, lam)[0] for lam in lambda_seq])
plt.plot(-np.log(lambda_seq), coef_seq+np.arange(0,0.06,0.01), label=["X"+str(j) for j in range(x.shape[1])]);
setting_plot(xlabel=r"$-\log(\lambda)$",ylabel=r"$\beta$",
title="Lasso")
plt.legend();
18
L=\frac{1}{2N}\|y-\beta_0-X\beta\|_2^2+\lambda\bigg\{\frac{1-\alpha}{2}\|\beta\|_2^2+\alpha\|\beta\|_1\bigg\}
とする。$|y-\beta_0-X\beta|_2^2$と$|\beta|_2^2$は微分可能であり、$|\beta|_1$は劣微分を利用すると、
0\in-\frac{1}{N}x_{j}(y-X\beta)+\lambda(1-\alpha)\beta_j+\lambda\alpha
\left\{\begin{array}{ll}
1&\beta_j>0\\
[-1,1]&\beta_j=0\\
-1&\beta_j<0
\end{array}\right.\\
=-\frac{1}{N}\sum_{i=1}^Nx_{i,j}(y_i-\sum_{k=1}^px_{i,k}\beta_k)+\lambda(1-\alpha)\beta_j+\lambda\alpha
\left\{\begin{array}{ll}
1&\beta_j>0\\
[-1,1]&\beta_j=0\\
-1&\beta_j<0
\end{array}\right.\\
=-\frac{1}{N}\sum_{i=1}^Nx_{i,j}(y_i-\sum_{k\neq j}^px_{i,k}\beta_k)+\bigg\{\frac{1}{N}\sum_{i=1}^Nx_{i,j}^2+\lambda(1-\alpha)\bigg\}\beta_j+\lambda\alpha
\left\{\begin{array}{ll}
1&\beta_j>0\\
[-1,1]&\beta_j=0\\
-1&\beta_j<0
\end{array}\right.
ここで、$r_{i,j}=y_i-\sum_{k\neq j}^px_{i,k}\beta_k$とおくと、
0\in -\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}+\bigg\{\frac{1}{N}\sum_{i=1}^Nx_{i,j}^2+\lambda(1-\alpha)\bigg\}\beta_j+\lambda\alpha
\left\{\begin{array}{ll}
1&\beta_j>0\\
[-1,1]&\beta_j=0\\
-1&\beta_j<0
\end{array}\right.
$\beta_j>0$のとき、
-\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}+\bigg\{\frac{1}{N}\sum_{i=1}^Nx_{i,j}^2+\lambda(1-\alpha)\bigg\}\beta_j+\lambda\alpha=0\\
\bigg\{\frac{1}{N}\sum_{i=1}^Nx_{i,j}^2+\lambda(1-\alpha)\bigg\}\beta_j=\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}-\lambda\alpha
$\lambda\geq0,\ 0\leq\alpha\leq1$であるから、
\beta_j>0\rightarrow \frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}>\lambda\alpha
$\beta_j=0$のとき、
-\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}+\lambda\alpha[-1,1]=0\\
-\lambda\alpha\leq\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}\leq\lambda\alpha
$\beta_j<0$のとき、
-\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}+\bigg\{\frac{1}{N}\sum_{i=1}^Nx_{i,j}^2+\lambda(1-\alpha)\bigg\}\beta_j-\lambda\alpha=0\\
\bigg\{\frac{1}{N}\sum_{i=1}^Nx_{i,j}^2+\lambda(1-\alpha)\bigg\}\beta_j=\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}+\lambda\alpha
$\lambda\geq0,\ 0\leq\alpha\leq1$であるから、
\beta_j<0\rightarrow \frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}<-\lambda\alpha
S_\lambda(x)=\left\{\begin{array}{ll}
x-\lambda & x>\lambda\\
0 & |x| \leq \lambda\\
x+\lambda & x<-\lambda
\end{array}\right.
とすると、
\begin{align}
\bigg\{\frac{1}{N}\sum_{i=1}^Nx_{i,j}^2+\lambda(1-\alpha)\bigg\}\beta_j&=
\left\{\begin{array}{ll}
\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}-\lambda\alpha & \frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}>\lambda\alpha\\
0 & -\lambda\alpha\leq\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}\leq\lambda\alpha\\
\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}+\lambda\alpha & \frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}<-\lambda\alpha
\end{array}\right.\\
&=S_{\lambda\alpha}\bigg(\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}\bigg)
\end{align}
したがって、
\hat{\beta}_j=\frac{S_{\lambda\alpha}\bigg(\frac{1}{N}\sum_{i=1}^Nx_{i,j}r_{i,j}\bigg)}{\frac{1}{N}\sum_{i=1}^Nx_{i,j}^2+\lambda(1-\alpha)}
となる。
19
def elastic_net(X, y, lam=0, alpha=1, beta=None):
n, p = X.shape
if beta is None:
beta = np.zeros(p)
X, y, X_bar, X_sd, y_bar = centralize(X,y)
eps = 1
while eps > 1e-5:
beta_old = beta.copy()
for j in range(p):
index = np.ones(p, dtype='bool')
index[j] = False
r = y.ravel() - np.sum(X[:, index]*beta[index], axis=1, keepdims=True).ravel()
z = (r.T@X[:,j]/n)
beta[j] = sort_th(lam*alpha, z) / (X[:,j].T@X[:,j]/n + lam*(1-alpha)/np.sqrt(np.sum(y-y_bar))**2/n)
eps = np.linalg.norm(beta - beta_old, 2)
beta = beta / X_sd
beta_0 = y_bar - X_bar@beta
return beta, beta_0
n = 500
x = np.zeros((n, 6))
z = np.random.normal(size=(n,2))
x[:,:3] = z[:,[0]] + np.random.normal(size=(n,3)) / 5
x[:,3:] = z[:,[1]] + np.random.normal(size=(n,3)) / 5
y = 3*z[:,0] - 1.5*z[:,1] + 2*np.random.normal(size=(n))
lambda_seq = np.arange(0.1, 20, 0.1)
coef_seq = np.array([elastic_net(x, y, lam, alpha=1)[0] for lam in lambda_seq])
plt.plot(-np.log(lambda_seq), coef_seq+np.arange(0,0.06,0.01), label=["X"+str(j) for j in range(x.shape[1])]);
setting_plot(xlabel=r"$-\log(\lambda)$",ylabel=r"$\beta$",
title="Lasso")
plt.legend();
20
def cv_linear_lasso(x, y, alpha=1, k=10):
lam_max = np.max((x.T@y)/(x.T@x))
lam_seq = np.array(range(100))**3 / 1e6 * lam_max
n = len(y)
m = int(n/k)
r = n%k
S_min = np.inf
for lam in lam_seq:
S = 0
for i in range(k):
if i < k-r:
index = list(range(i*m,i*m+m))
else:
index = list(range(i*m+(i-k+r),i*m+(m+i-k+r+1)))
_index = list(set(range(n))-set(index))
beta, beta0 = elastic_net(x[_index,],y[_index], lam, alpha)
z = np.linalg.norm((y[index] - beta0 - x[index]@beta), 2)
S = S + z**2
if S < S_min:
S_min = S.copy()
lam_best = lam.copy()
beta0_best = beta0.copy()
beta_best = beta.copy()
return lam_best, beta0_best, beta_best, S_min
以上となります。
この手の勉強は会社で言っても反応悪いのでこういったところに投稿させていただいています。
次回
一般化線形回帰