pythonとopencvを使って画像処理を勉強していきます。
今回はschikit-learnやschikit-imageなども使用します。
前回
python+opencvで画像処理の勉強6 2値画像処理
領域処理のための特徴量
領域のテクスチャ
繰り返しの輝度パターンをテクスチャと呼びます。
コンピュータがテクスチャを扱うためにはその特徴量を数値化する必要があります。
2次元フーリエ変換による周波数特徴量
2次元フーリエ変換の結果$F(u,v)$を用いて、パワースペクトル$p(u,v)$、その極座標$p(r,\theta)$を求めます。
さらに、幅$\Delta\theta$を持つ角度\thetaの扇状領域$p(\theta)$と、幅$\Delta r$を持つ半径$r$の同心円状領域$p(r)$を、以下の式により求めます。
p(\theta)=\sum_{\theta'=\theta-\frac{\Delta\theta}{2}}^{\theta+\frac{\Delta\theta}{2}}\sum_{r=0}^{\infty}p(\theta',r)\\
p(r)=\sum_{r'=r-\frac{\Delta r}{2}}^{r+\frac{\Delta r}{2}}\sum_{\theta=0}^{2\pi}p(\theta,r')
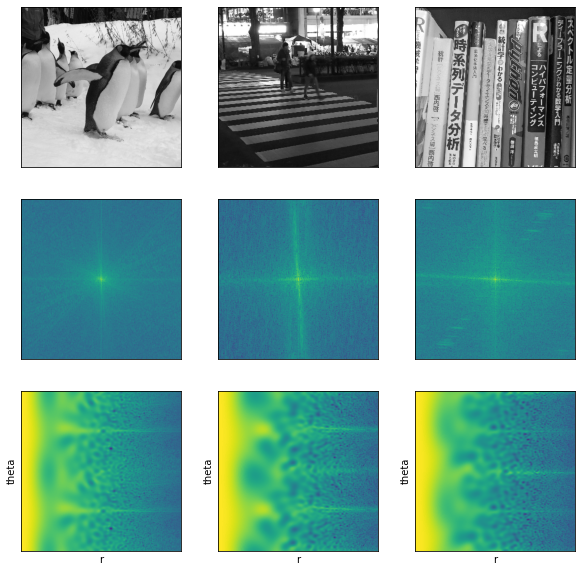
ここでは、パワースペクトルと極座標変換した結果を示します。
極座標変換はcv2.warpPolarを使用します。
import numpy as np
import matplotlib.pyplot as plt
import cv2
def make_power_sp(img):
"""パワースペクトル"""
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
return magnitude_spectrum
def make_polar_img(img):
"""極座標へのマッピング"""
h = img.shape[0]
w = img.shape[1]
l = np.sqrt(w*w + h*h)
m = l/np.log(l)
center = (w/2, h/2)
flags = cv2.INTER_LANCZOS4 + cv2.WARP_POLAR_LOG
p_a = cv2.warpPolar(img, (w, h), center, m, flags)
return p_a
imgs = np.array([img_gray1, img_gray2, img_gray3])
fig, ax = plt.subplots(3, 3, figsize=(10, 10), subplot_kw=({"xticks":(), "yticks":()}))
for i in range(3):
ft_img = make_power_sp(imgs[i])
p_img = make_polar_img(ft_img)
ax[0][i].imshow(imgs[i], cmap = 'gray')
ax[1][i].imshow(ft_img, cmap = 'viridis')
ax[2][i].imshow(p_img, cmap = 'viridis')
ax[2][i].set_xlabel('r')
ax[2][i].set_ylabel('theta')
ガボールフィルタによる局所周波数特性
ガボールフィルタとは、正弦波・余弦波にガウス関数で窓をかけた関数のことです。
パラメータを操作して様々な方向と強度を持つフィルタを多数準備して特徴抽出を行います。
このフィルタ群をフィルタバンクと呼び、抽出された特徴量の群はtextonといいます。
2次元のガボールフィルタの式を以下に表します。
g(x,y,\lambda,\varphi)=\exp{(-\frac{x^2+y^2}{2\sigma^2})}\exp{(2\pi\lambda i(x\cos{\varphi}+y\sin{\varphi}))}
ガボールフィルタのフィルタバンクの例を示します。
様々な方向を持つフィルタ群となります。
# cv2.getGaborKernel((ksize, sigma, theta, lambd, gamma, psi)
# ksize フィルタのサイズ
# sigma 波の出てくる幅
# theta 角度
# lambd 波長
# gamma 広がり
# psi 位相
thetas = [0, -22.5, -45, -67.5, -90, -112.5, -135, -157.5]
fig, ax = plt.subplots(2, 4, figsize=(12, 6), subplot_kw=({"xticks":(), "yticks":()}))
for i in range(8):
gabor = cv2.getGaborKernel((20, 20), 2, np.radians(thetas[i]), 3, 0.6, 0)
ax[i//4][i%4].imshow(gabor, 'gray')
方向は同じで波長の異なるフィルタの例を示します。
fig, ax = plt.subplots(2, 4, figsize=(12, 6), subplot_kw=({"xticks":(), "yticks":()}))
for i in range(8):
gabor = cv2.getGaborKernel((20, 20), 2, np.radians(thetas[i]), 2, 0.6, 0)
ax[i//4][i%4].imshow(gabor, 'gray')
これらのフィルタバンクで変換された画像を示します。
fig, ax = plt.subplots(2, 4, figsize=(16, 8), subplot_kw=({"xticks":(), "yticks":()}))
sum_img = np.zeros(img_gray3.shape)
for i in range(8):
gabor = cv2.getGaborKernel((20, 20), 2, np.radians(thetas[i]), 3, 0.6, 0)
dst = cv2.filter2D(img_gray3, -1, gabor)
sum_img += dst
ax[i//4][i%4].imshow(dst, 'gray')
これらを足し合わせた画像は次のようになります。
plt.imshow(sum_img, 'gray');
同時生起行列を用いた統計的特徴量
テクスチャの統計的特徴量を求めるために、同時生起行列を用いる方法があります。
これは、離れた2つの場所にある画素対の値から、画素値の一様性、方向性、コントラストなどの性質を表す特徴量を求めるものであります。
ある画素$i$と、$i$から離れた位置にある画素$j$の画素対を考え、画素$i$と画素$j$の相対的な位置を$\delta=$とします。
それぞれの画素値を$L_{i}$、$L_{j}$とし、画素値の対$(L_{i},L_{j})$が生じる出現頻度で、ある同時生起行列$\boldsymbol{H_{\delta}}(L_{i},L_{j})$を考えます。
ここで、出現頻度$\boldsymbol{H_{\delta}}(L_{i},L_{j})$を正規化し、確率に変換した同時生起行列を$\boldsymbol{P_{\delta}}(L_{i},L_{j})$とします。
ディジタル画像では、$\delta=$は離散的な値を取り、$d=1$の場合、$\theta$がとりうる値は、0°,45°,90°,135°,180°,225°,270°,315°となります。
点対称の関係も同じものとみなすと、$\theta$がとりうる値は、0°,45°,90°,135°となります。
同時生起行列の例を示します。
以下のような2値画像の場合、
\left[\begin{array}{cccc}
1&0&0&1\\
0&1&0&0\\
0&1&0&1\\
1&0&1&1
\end{array}\right]
$\boldsymbol{H}<1,0°>$は、
\left[\begin{array}{cc}
4&9\\
9&2
\end{array}\right]
のようになります。ここで、縦方向は画素$j$の値であり上から0,1、横方向は画素$i$の値であり左から0,1に対応しています。
主な特徴量
同時生起行列を用いて計算する主な特徴量に、以下の7種類があります。ここで、$L$は画素値のレベルを表します。
エネルギー:$$ENR=\sum_{L_{i}=0}^{L-1}\sum_{L_{j}=0}^{L-1}{P_{\sigma}(L_{i},L_{j})}^2$$
コントラスト:$$CNT=\sum_{k=0}^{L-1}k^2P_{x-y}(k)$$
相関:$$CRR=\frac{\sum_{L_{i}=0}^{L-1}\sum_{L_{j}=0}^{L-1}L_{i}L_{j}P_{\sigma}(L_{i},L_{j})-\mu_{x}\mu_{y}}{\sigma_{x}\sigma_{y}}$$
分散:$$VAR=\sum_{L_{i}=0}^{L-1}\sum_{L_{j}=0}^{L-1}(L_{i}-\mu_{x})^2P_{\sigma}(L_{i},L_{j})$$
エントロピー:$$EPY=-\sum_{L_{i}=0}^{L-1}\sum_{L_{j}=0}^{L-1}P_{\sigma}(L_{i},L_{j})\log{{P_{\sigma}(L_{i},L_{j})}}$$
サムエントロピー:$$SEP=-\sum_{k=0}^{2L-2}P_{x+y}(k)\log{{P_{x+y}(k)}}$$
逆差分モーメント:$$IDM=\sum_{L_{i}=0}^{L-1}\sum_{L_{j}=0}^{L-1}\frac{1}{1+(L_{i}-L_{j})^2}P_{\sigma}(L_{i},L_{j})$$
ただし、
\mu_{x}=\sum_{L_{i}=0}^{L-1}L_{i}P_{x}(L_{i}),\quad \mu_{y}=\sum_{L_{j}=0}^{L-1}L_{j}P_{y}(L_{j})\\
\delta_{x}^2=\sum_{L_{i}=0}^{L-1}(L_{i}-\mu_{x})^2P_{x}(L_{i}),\quad \delta_{y}^2=\sum_{L_{j}=0}^{L-1}(L_{j}-\mu_{y})^2P_{y}(L_{j})\\
P_{x}(L_{i})=\sum_{L_{j}=0}^{L-1}P_{\sigma}(L_{i},L_{j}),\quad P_{y}(L_{j})=\sum_{L_{i}=0}^{L-1}P_{\sigma}(L_{i},L_{j})\\
P_{x-y}(k)=\sum_{L_{i}=0}^{L-1}\sum_{L_{j}=0}^{L-1}P_{\sigma}(L_{i},L_{j}) \quad ただし、|L_{i}-L_{j}|=kを満たす\\
P_{x+y}(k)=\sum_{L_{i}=0}^{L-1}\sum_{L_{j}=0}^{L-1}P_{\sigma}(L_{i},L_{j}) \quad ただし、|L_{i}+L_{j}|=kを満たす
ここではschikit-imageを使用して計算を行います。
また、上で紹介したもののうち一部のみを計算します。
実行には少し時間がかかります。
from skimage.feature import greycomatrix, greycoprops
def make_glcm_features(input_image, feature):
glcm_feature = np.zeros((input_image.shape[0], input_image.shape[1]))
for i in range(input_image.shape[0] ):
#if i % 10 == 0:
# print(i)
for j in range(input_image.shape[1] ):
# 境界値処理
if i <3 or j <3 or i > input_image.shape[0] - 4 or j > input_image.shape[1] - 4:
glcm_feature[i,j]= 0
continue
# 7x7のウィンドウで画像を切り取る
glcmWindow = input_image[i-3: i+4, j-3 : j+4]
# 0度と90度の同時生起行列を計算する
glcm_x = greycomatrix(glcmWindow, [1], [0], levels=256, symmetric=True)
glcm_y = greycomatrix(glcmWindow, [1], [90], levels=256, symmetric=True)
# テクスチャ特徴量を計算
texture_feature_x = greycoprops(glcm_x, feature)
texture_feature_y = greycoprops(glcm_y, feature)
glcm_feature[i,j] = (texture_feature_x + texture_feature_y)/2
return glcm_feature
feature_names = ['contrast', 'dissimilarity', 'homogeneity', 'energy', 'ASM', 'correlation']
glcm_feature = np.array([make_glcm_features(img_gray, feature_name) for feature_name in feature_names])
計算結果を表示します。
fig, ax = plt.subplots(2, 3, figsize=(12, 8), subplot_kw=({"xticks":(), "yticks":()}))
for i in range(6):
ax[i//3][i%3].imshow(glcm_feature[i])
ax[i//3][i%3].set_title(feature_names[i])
別の画像でも試してみます。
glcm_feature = np.array([make_glcm_features(img_gray3, feature_name) for feature_name in feature_names])
fig, ax = plt.subplots(2, 3, figsize=(12, 8), subplot_kw=({"xticks":(), "yticks":()}))
for i in range(6):
ax[i//3][i%3].imshow(glcm_feature[i])
ax[i//3][i%3].set_title(feature_names[i])
領域分割処理
領域分割処理のアプローチ
画像上で近傍の画素を特徴量に基づいて、階層的に統合する方法、画素の持つ属性値のパラメータ空間でクラスタリングする方法などがあります。
隣接画素の階層的な統合による領域分割処理
類似した特徴量を持ち空間的に隣接した画素の集合に画像を分割する代表的な手法が領域統合法です。
- ラスタスキャンによって、ラベルの付いていない画素を注目画素とし、新しくラベルを付けます。
- 注目画素の4(8)近傍で、同じ画素があれば注目画素と同じラベルを付けます。
- 新しくラベルを付けた画素を注目画素として、2の処理を行います。
- 2の操作で新しくラベルを付ける画素がなければ、1の処理に戻ります。
- すべての画素にラベルが付いたところで処理を終了します。
- 同じラベルを持つ画素の画素値の、平均値を全て求めます。
- すべての未処理のラベルを持つ画素の集合および、統合されていない画素の集合に対して、隣接する画素の集合のなかで、
上記平均値の差分が最小の画素の集合と統合し、新しいラベルを統合された領域のすべての画素に付けます。 - すべての画素の集合を未処理のラベルとして、6~8の処理を繰り返します。
画素特徴量のパラメータ空間でのクラス分けによる領域分割処理
画素の空間的な位置関係を全く考慮せず、画素単位に特徴量を計算し、画素単位でクラス分けをします。
詳しくは9 パターン認識で説明します。
画素特徴を効率よくクラス分けするミーンシフト
ここでは、ミーンシフト法を用いた画像の領域分割の例を示します。
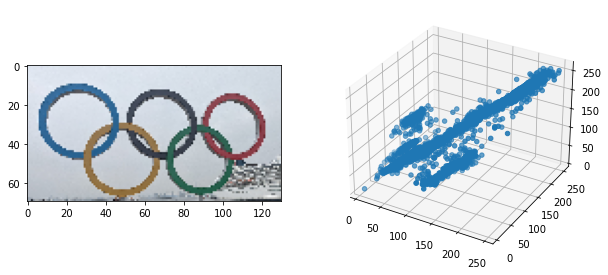
まず、使用する画像と画素値の分布を確認します。
from mpl_toolkits.mplot3d import Axes3D
rgb_img = img_rgb.copy()
fig = plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(rgb_img)
plt.subplot(1, 2, 2)
ax = fig.add_subplot(122, projection='3d')
ax.scatter3D(rgb_img[:,:,0], rgb_img[:,:,1], rgb_img[:,:,2])
各画素のRGBの画素値と座標を説明変数とします。
import pandas as pd
rgb0 = rgb_img[:,:,0]
rgb1 = rgb_img[:,:,1]
rgb2 = rgb_img[:,:,2]
x1 = range(0,rgb_img.shape[1])
x2 = range(0,rgb_img.shape[0])
x1, x2 = np.meshgrid(x1,x2)
rgb = np.array([rgb0, rgb1, rgb2, x1, x2]).reshape(5,rgb_img.shape[0]*rgb_img.shape[1])
df = pd.DataFrame(rgb.T)
df.columns = ['red', 'green', 'blue', 'x1', 'x2']
df.head()
比較のため、k-meansとMean-shiftでクラスタリングを行います。
Mean-shiftは画像サイズが大きいと時間がかかります。
from sklearn import cluster
from sklearn.cluster import MeanShift,estimate_bandwidth
# k-means
km=cluster.KMeans(n_clusters=6)
z_km=km.fit(df)
# MeanShift
bwidth = estimate_bandwidth(df.values,quantile=0.15,n_samples=200)
ms = cluster.MeanShift(seeds=df.values, bandwidth=bwidth)
ms.fit(df.values)
画素値のプロットとクラスタリングの結果を確認します。
k-meansに比べてMean-shiftの方がバランスよく分けられていることが分かります。
import matplotlib.cm as cm
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
ax[0].scatter(df["red"], df["blue"], c=cm.hsv(ms.labels_/len(ms.cluster_centers_)))
ax[0].scatter(ms.cluster_centers_[:,0], ms.cluster_centers_[:,2],s=250, marker='*',c='orange')
ax[0].set_title("Mean Shift");
ax[1].scatter(df["red"], df["blue"], c=cm.hsv(z_km.labels_/len(z_km.cluster_centers_)))
ax[1].scatter(z_km.cluster_centers_[:,0],z_km.cluster_centers_[:,2],s=250, marker='*',c='orange')
ax[1].set_title("k-means");
画像で確認します。
黒と緑がうまく分類できていませんが、色ごとに分けられていることが確認できます。
fig, ax = plt.subplots(1, 3, figsize=(20, 10), subplot_kw=({"xticks":(), "yticks":()}))
ax[0].imshow(rgb_img)
ax[1].imshow(labels.reshape(rgb_img.shape[0],rgb_img.shape[1]),cmap='hsv')
ax[1].set_title("Mean Shift");
ax[2].imshow(z_km.labels_.reshape(rgb_img.shape[0],rgb_img.shape[1]),cmap='hsv')
ax[2].set_title("k-means");
対象物と背景の間のエッジを利用した領域分割処理
対象領域がエッジで禍根れているときは、エッジを閉曲線として抽出する**スネーク(動的輪郭モデル)**によって領域分割が行えます。
スネークは、対象物体を囲む閉曲線を初期値として与え、徐々に閉曲線が縮んでいき、エッジの境界に張り付いていきます。
閉曲線のエネルギー$E_{S}$を以下のように定め、$E_{S}$が最小になるように閉曲線を求めます。
E_{S}=\int_{0}^{1}E_{internal}(\nu(s))ds+\int_{0}^{1}E_{image}(\nu(s))ds+\int_{0}^{1}E_{external}(\nu(s))ds
ただし、$\nu(s)$は$s(0\leq s\leq1)$を媒介変数とする閉曲線で$\nu(s)=(x(s),y(s))$です。
$E_{internal}$は、閉曲線の連続性や滑らかさを表すエネルギー
$E_{image}$は、画像のエッジの強度に基づくエネルギー
$E_{external}$は、ユーザーが望むような任意のエネルギーを付加するための項である。
$E_{internal}$は、連続性のエネルギー$E_{continuity}$と、滑らかさのエネルギー$E_{curvature}$の加重和で、以下のように表されます。
E_{internal}=\alpha E_{continuity}(\nu(s))+\beta E_{curvature}(\nu(s))
$E_{continuity}=|d\nu/ds|^2$は、$\nu(s)$の1次微分値の2乗であり、閉曲線の長さを短くしようとする。
$E_{curvature}=|d^2\nu/ds^2|^2$は、$\nu(s)$の2次微分値の2乗であり、閉曲線の滑らかさを表す。
$\alpha$と$\beta$はそれぞれエネルギーの重みである。
$E_{image}$はエッジのある場所で小さくなり、$E_{image}=-|\nabla I(\nu(s))|$である。
ここでは、schikit-imageを使用して実装を行います。
オレンジの点線が初期位置として赤い線が求められています。
from skimage.segmentation import active_contour
from skimage.filters import gaussian
s = np.linspace(0, 2*np.pi, 400)
r = 150 + 130*np.sin(s)
c = 200 + 130*np.cos(s)
init = np.array([r, c]).T
snake = active_contour(gaussian(img_gray,3, preserve_range=False), init, alpha=0.015, beta=10, gamma=0.001)
plt.imshow(img_rgb)
plt.plot(snake[:,1], snake[:,0], c='red')
plt.plot(init[:, 1], init[:, 0], '--', c='orange')
plt.xticks([]);
plt.yticks([]);
グラフカットを用いた領域分割処理
ある画像において、あらかじめ対象と背景の一部の位置が与えられている条件下で、対象と背景には画素値に違いがあるという仮定のもとで、
全画像を対象と背景の2種類にラベル付けする方法として、グラフカットがあります。
まず、枠線を与えて求める例を示します。
img = img_rgb.copy()
mask = np.zeros(img.shape[:2],np.uint8)
newmask=np.zeros(img.shape[:2],np.uint8)
newmask[150:151,150:250] = 1
bgdModel = np.zeros((1,65),np.float64)
fgdModel = np.zeros((1,65),np.float64)
rect = (90,90,280,200)
mask, bgdModel, fgdModel = cv2.grabCut(img, mask, rect, bgdModel, fgdModel, 5, cv2.GC_INIT_WITH_RECT)
mask2 = np.where((mask==2)|(mask==0),0,1).astype('uint8')
result = img*mask2[:,:,np.newaxis]
cv2.rectangle(img, (90,90), (280,200), (255, 0, 0))
fig, ax = plt.subplots(1, 2, figsize=(15, 5), subplot_kw=({"xticks":(), "yticks":()}))
ax[0].imshow(img);
ax[1].imshow(result);
次にマスク画像を与えて求める方法を示します。
2番目の図がマスク画像です。
img = img_rgb.copy()
mask = np.zeros(img.shape[:2],np.uint8)
mask[90:210,90:280] = 3
mask[140:160,150:250] = 1
maskc = mask.copy()
bgdModel = np.zeros((1,65),np.float64)
fgdModel = np.zeros((1,65),np.float64)
mask, bgdModel, fgdModel = cv2.grabCut(img,mask,None, bgdModel,fgdModel,5,cv2.GC_INIT_WITH_MASK)
mask2 = np.where((mask==2)|(mask==0),0,1).astype('uint8')
result = img*mask2[:,:,np.newaxis]
fig, ax = plt.subplots(1, 3, figsize=(15, 5), subplot_kw=({"xticks":(), "yticks":()}))
ax[0].imshow(img);
ax[1].imshow(maskc);
ax[2].imshow(result);
Watershedアルゴリズムを使った画像の領域分割
最後にWatershedアルゴリズムを使用した領域分割の例を示します。
2値化処理の後に、距離画像へと変換してさらに2値化処理を行いラベリングをします。
そして、cv2.watershedを使って領域分割を行います。
# 2値化
ret, thresh = cv2.threshold(img_gray,170,255,cv2.THRESH_BINARY_INV)
kernel = np.ones((3,3),np.uint8)
opening = cv2.morphologyEx(thresh,cv2.MORPH_OPEN,kernel, iterations = 2)
sure_bg = cv2.dilate(opening,kernel,iterations=3)
# 距離画像
dist_transform = cv2.distanceTransform(sure_bg,cv2.DIST_L2,3)
# 2値化
ret, sure_fg = cv2.threshold(dist_transform,0.28*dist_transform.max(),255,0)
sure_fg = np.uint8(sure_fg)
unknown = cv2.subtract(sure_bg,sure_fg)
# ラベリング
ret, markers = cv2.connectedComponents(sure_fg)
markers = markers+1
markers[unknown==255] = 0
markers = cv2.watershed(img_rgb, markers)
img_rgb[markers == -1] = [255,0,0]
plt.imshow(markers)
plt.xticks([]);
plt.yticks([]);
contours, hierarchy = cv2.findContours(markers.copy(), cv2.RETR_CCOMP, cv2.CHAIN_APPROX_SIMPLE)
for i in range(len(contours)):
if hierarchy[0][i][3] == -1:
cv2.drawContours(img_rgb2, contours, i, (255, 0, 0), 1)
plt.imshow(img_rgb2);
plt.xticks([]);
plt.yticks([]);
次回
パターン・図形・特徴の検出とマッチング
参考
ディジタル画像処理[改訂第二版] | ディジタル画像処理編集委員会 |本 | 通販 | Amazon