エンジニアがプログラムの各所に現れる条件文を考えるとき、論理学の知識が必要になってきます。
この記事ではエンジニアが知っておくべき論理学の定理・法則を4つに絞ってまとめました。
基本的な演算子として、以下の記号は理解できているものとします。
| 日本語 | 記号 | 英語 |
|---|---|---|
| 否定 | $ \neg $ | NOT |
| 論理積 | $ \wedge $ | AND |
| 論理和 | $ \vee $ | OR |
二重否定
まずは、否定の否定は肯定、という二重否定の法則です。
論理式 $ A $ の否定 $ \neg A $ もまた論理式ですので、さらにその否定 $ \neg \neg A $ を考えると元の論理式 $ A $ と同値となります。
\lnot \lnot A\Leftrightarrow A
分配法則
命題 $ A $ と、 $ B $ と $ C $ の論理和 $ ( B \vee C ) $ との論理積は、
$ A $ と $ B $ の論理積 ・ $ A $ と $ C $ の論理積、の論理和となります。
と文章で書いてもわかりづらいですよね。
論理式で書くと以下のようになります。
A \wedge ( B \vee C ) \Leftrightarrow ( A \wedge B ) \vee ( A \wedge C )
これは論理和と論理積を交換しても成り立ちます。
A \vee ( B \wedge C ) \Leftrightarrow ( A \vee B ) \wedge ( A \vee C )
ド・モルガンの法則
命題 $ A $ と 命題 $ B $ の論理和の否定は、命題 $ A $ の否定と 命題 $ B $ の否定との論理積と同値となります。中学校で習うド・モルガン (De Morgan's laws)の法則ですね。
\lnot ( A\wedge B) \Leftrightarrow \neg A \vee \neg B
AND 全体にかかっている否定(NOT)を、各命題に分配すると、OR でつなぐ形になるということです。
これも論理和と論理積を置き換えても成り立ちます。
\neg ( A\vee B) \Leftrightarrow \neg A\wedge \neg B
否定でくくる命題の数が増えても成り立ちます。
\neg ( A_1 \wedge A_2 \wedge \cdots \wedge A_{n}) \Leftrightarrow \neg A_1 \vee \neg A_2 \vee \cdots \vee \neg A_n
\neg ( A_1 \vee A_2 \vee \cdots \vee A_{n}) \Leftrightarrow \neg A_1 \wedge \neg A_2 \wedge \cdots \wedge \neg A_n
選言標準形
これまで挙げてきた「二重否定」の除去、分配法則、ド・モルガンの法則で変換することで、あらゆる論理式は、命題(またはその否定)の論理積の論理和で表すことができます。
これを選言標準形 (Disjunctive Normal Form = DNF)と呼びます。
論理式で書くと、以下のように AND だけで括られた論理式が OR でつながっているような形です。
( A_1 \wedge A_2 \wedge \cdots \wedge A_{n}) \vee (B_1 \wedge B_2 \wedge \cdots \wedge B_n)
\vee (C_1 \wedge C_2 \wedge \cdots \wedge C_n) \vee \cdots
個々の命題は否定でも OKですし、 OR でつなぐ論理式は $ (A \wedge B) \vee C $ の $ C $ のように単体の命題でも大丈夫です。
以下の論理式を選言標準形に変換してみます。
A \vee ( B \wedge \neg (C \wedge \neg D ) )
ド・モルガンの法則により $ \neg ( C \wedge \neg D ) $ を変換します。
A \vee ( B \wedge (\neg C \vee \neg \neg D ) )
$ \neg \neg D $ の二重否定を除去します。
A \vee ( B \wedge (\neg C \vee D) )
$ B \wedge (\neg C \vee D) $ を分配法則で変換します。
A \vee (( B \wedge \neg C ) \vee ( B \wedge D ))
隣り合う論理和については、どのような順番で論理和を作用させても同値なことから(結合法則)、括弧をはずして選言標準形の出来上がりです。
A \vee ( B \wedge \neg C ) \vee ( B \wedge D )
あらゆる論理式を選言標準形にすることができますので、
ユーザーに検索条件を自由に入力してもらうUIを考えるときなどに応用が効きます。
AND で括った条件グループを ORでつなぐようなユーザーインターフェースを作成すれば、
理論上はあらゆる条件を表現できます。
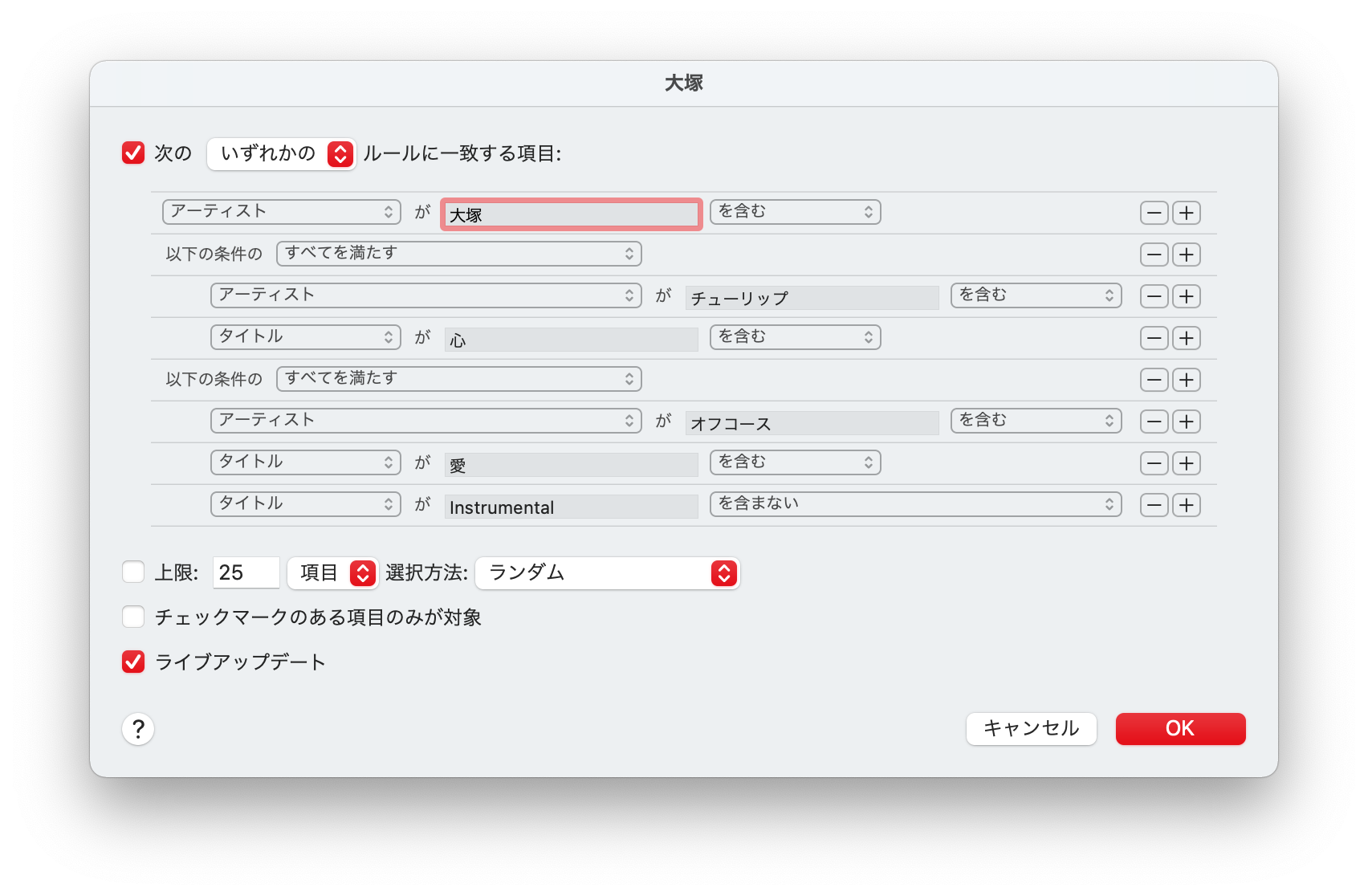
例えば Apple Musicでスマートプレイリストの条件を入力するウィンドウでは選言標準形での設定が可能です。(条件を入れ子にするには Optionキーを押しながら「+」をクリックします)
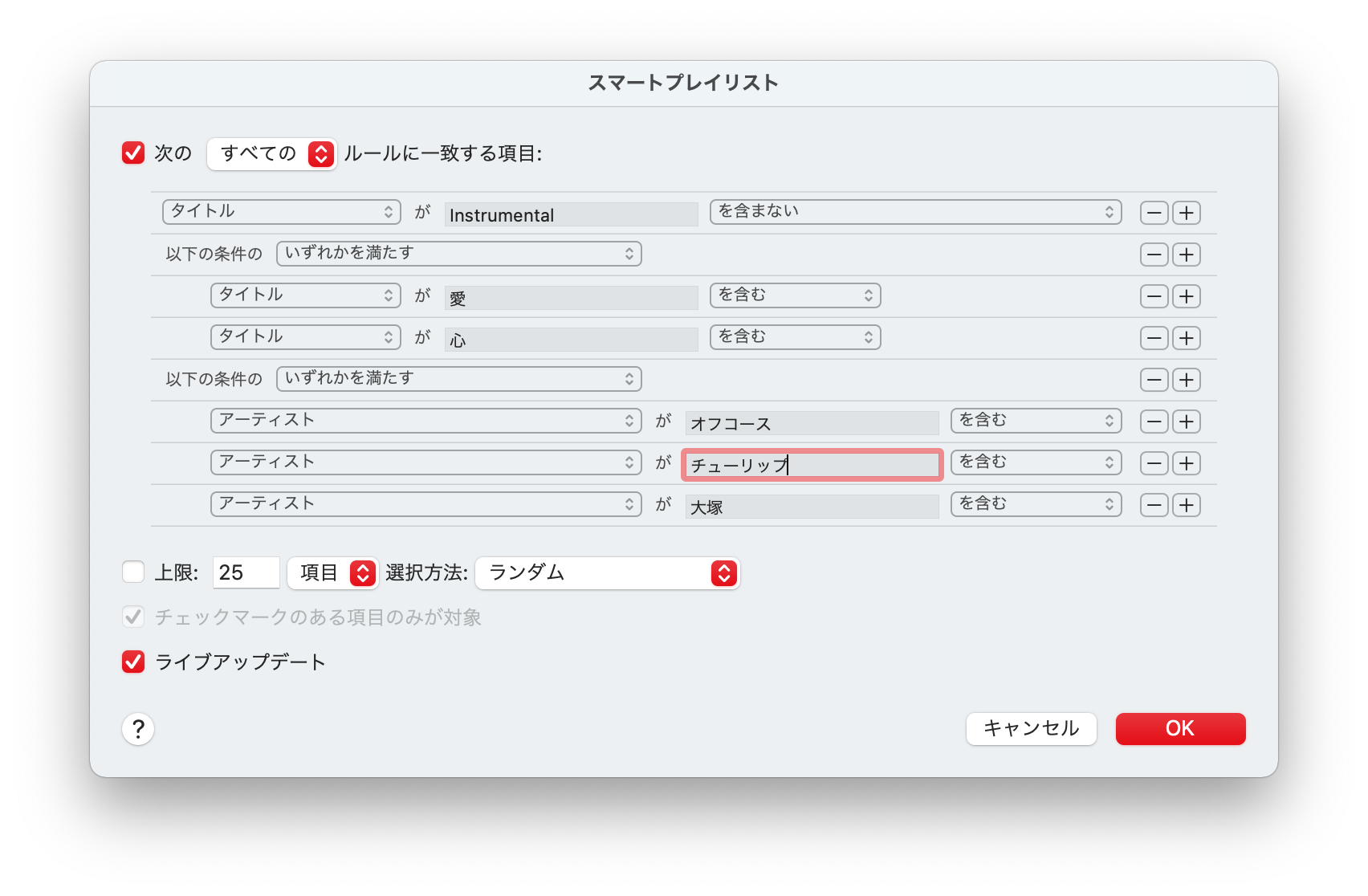
実は、ORで括った論理式を AND でつないだものを連言標準形 (Conjunctive normal form = CNF)と言って、これもあらゆる論理式を表すことができます。さきのスマートプレイリストの条件設定ウィンドウは、連言標準形での設定も可能です。
分配法則もド・モルガンの法則もそうですが、AND と OR はいろいろな法則上で交換可能です。面白いですよね。
参考