下式で定義される関数$f(\textbf{x})$を用いて、入力ベクトル$\textbf{x}=(x_1, x_2, \cdots , x_N)$の2値分類を行うことを考える。
f(\textbf{x}) = \phi(\sum_{p=1}^{P} \sum_{n=1}^{N} w_{n,p} \, {x_n} ^p + w_{0})\\
\\
\phi(y) =
\left\{
\begin{array}{l}
1 \quad (y \geq 0) \\
-1 \quad (otherwise)
\end{array}
\right.
ここで、$w_{n,p}$は重みパラメータ、$N$は入力ベクトル$\textbf{x}$の次元、$P$は多項式の次数である。重みパラメータ$w_{n,p}$は平均2乗誤差
l(\textbf{W}) = \sum_{i=1}^{I} (y_i - f(\textbf{x}_i))^2
を確率的勾配降下法により最小化することにより得られる。学習時の重みパラメータ$w_{n,p}$更新式の一例を下記に示す。
w_{0} \leftarrow w_{0} + \eta \sum_{i=1}^{I} (y_i - f(\textbf{x}_i)) \\
w_{n,p} \leftarrow w_{n,p} + \eta \sum_{i=1}^{I} ((y_i - f(\textbf{x}_i)) ( \sum_{n=1}^{N} {x_{n,i}} \, ^{p} ))
$\eta$は学習率、$(\textbf{x}_i, y_i)$は$i$番目の教師データ、$I$はバッチサイズを表している。
$P=1$の時、関数$f(\textbf{x})$はよく知られている単純パーセプトロンに一致し、関数$\phi$に入力されるのは$\textbf{x}$の線形関数となる。一方、$P>1$の時には、関数$\phi$に入力されるのは$\textbf{x}$の多項式であり、線形関数ではなくなる。次数$P$を高くすることで、関数$f(\textbf{x})$の非線形性を強くすることができる。関数$f(\textbf{x})$は単純パーセプトロンを非線形化したものと考えられる。
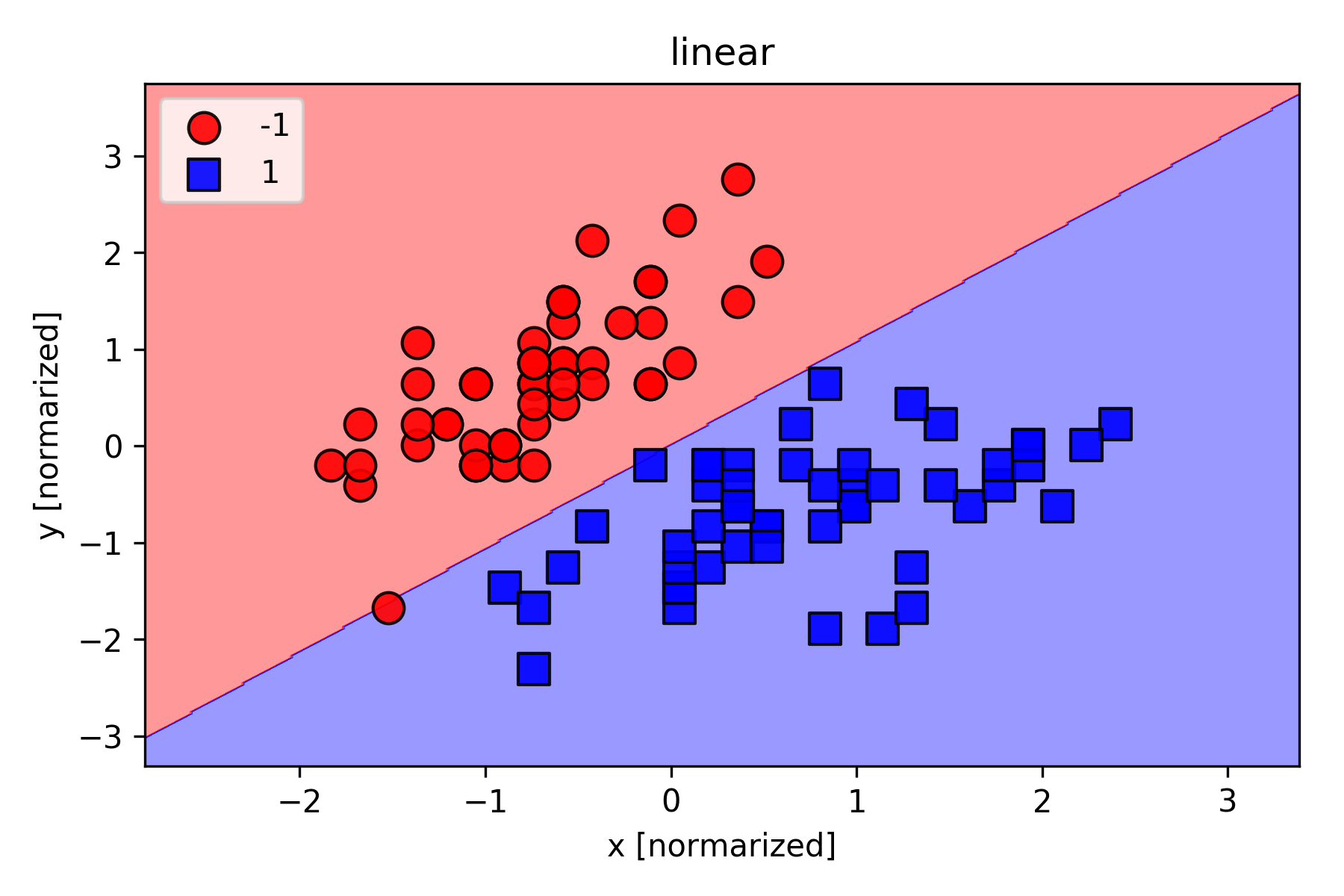
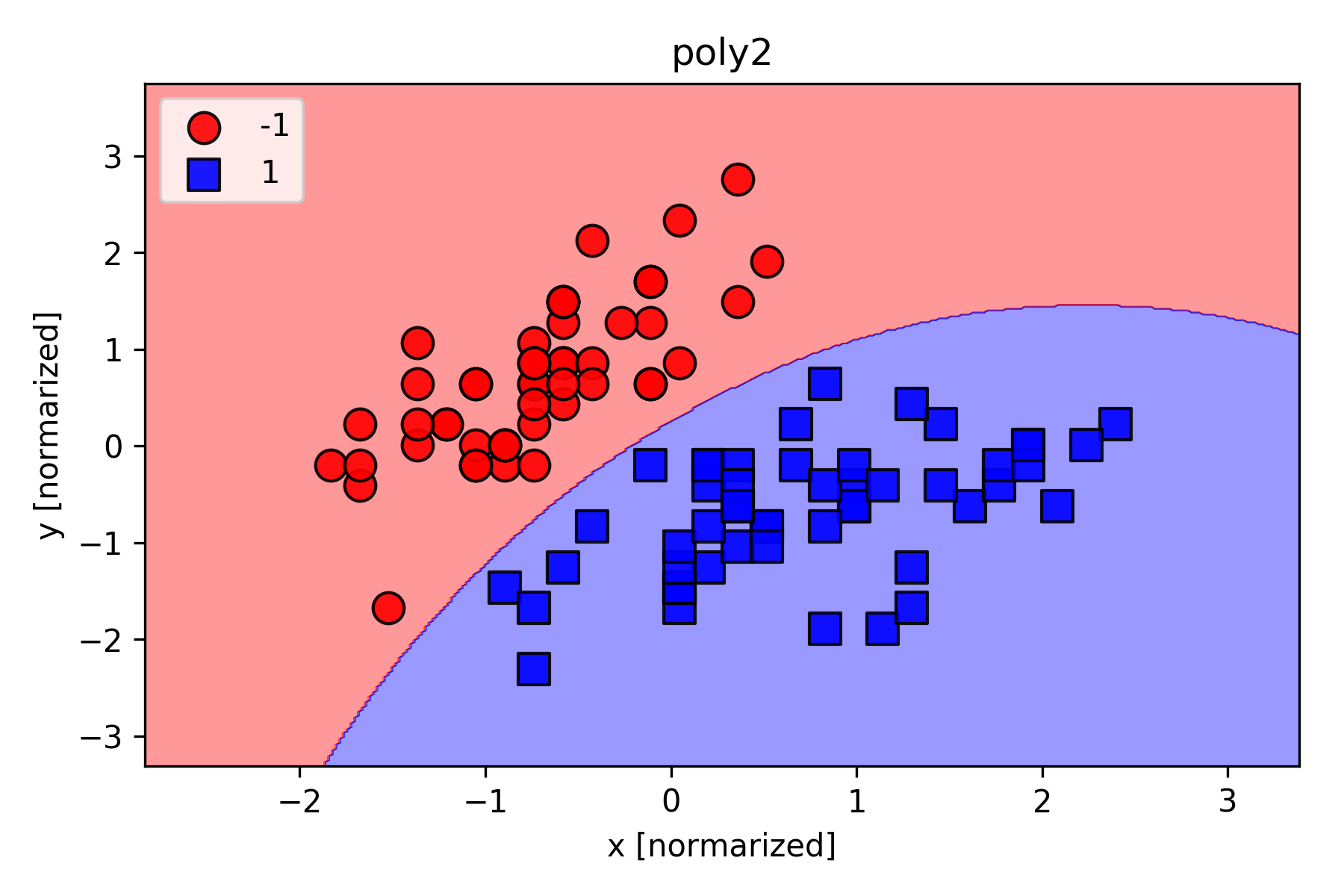
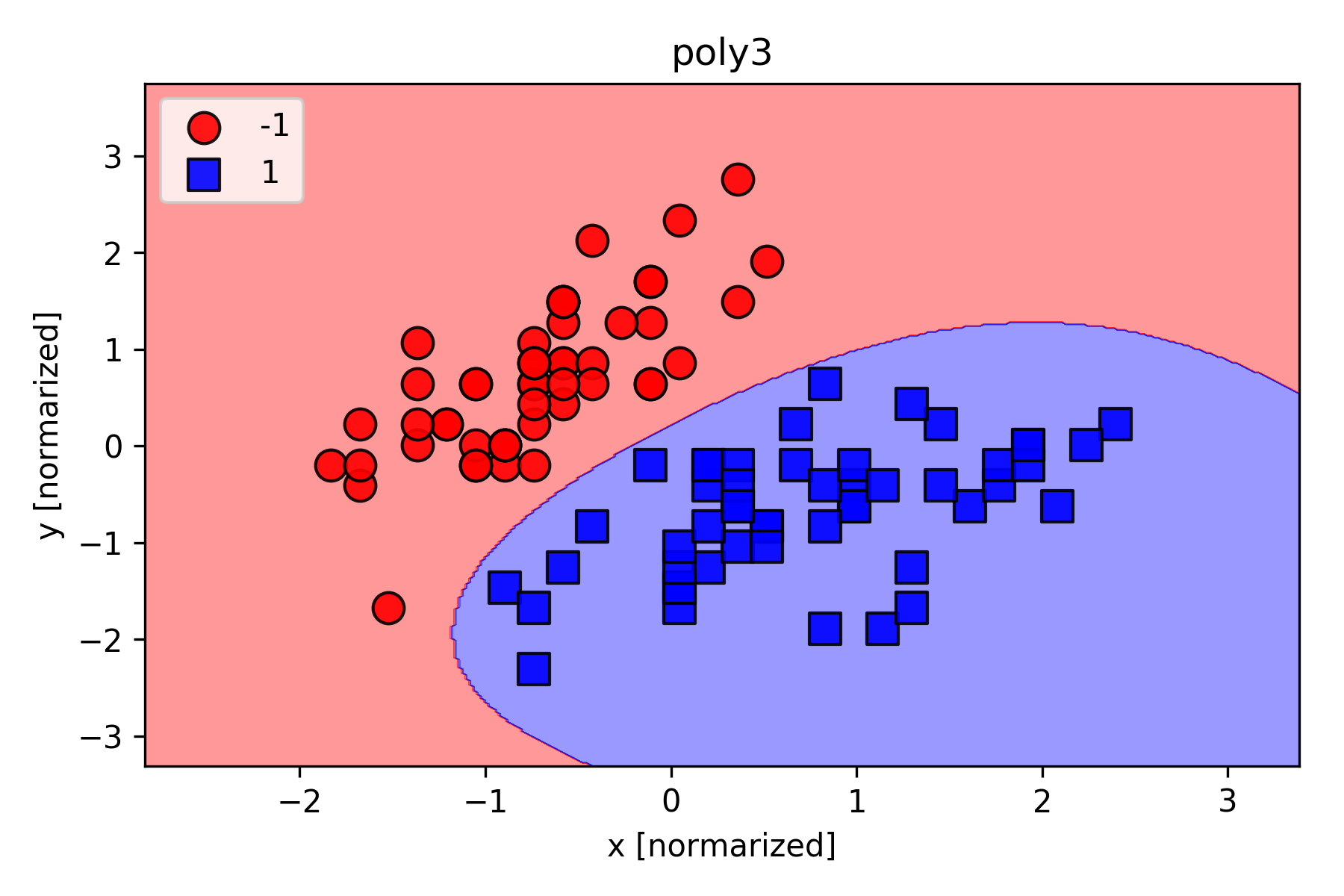
次数$P$の影響をみるために、Irisのデータセットを用いて学習を行い、分類結果を可視化してみた。実験結果を下記に示す。
linearと書いてあるのが次数$P=1$の時の結果(単純パーセプトロン)で、poly2, poly3と書いてあるのが次数$P=2$, $P=3$の時の結果。次数$P$を高くすることで、複雑な分類にも対応できるようになることが分かる。
下記は実験に使用したソースコード。
import numpy as np
from numpy.random import *
class MyClass(object):
def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None, model='linear'):
self.eta = eta
self.n_iter = n_iter
self.w_initialized = False
self.shuffle = shuffle
self.model=model
if random_state:
seed(random_state)
def fit(self, X, y):
self._initialize_weights(X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
if self.shuffle:
X, y = self._shuffle(X, y)
cost = []
for xi, target in zip(X, y):
cost.append(self._update_weights(xi, target))
avg_cost = sum(cost) / len(y)
self.cost_.append(avg_cost)
return self
def _shuffle(self, X, y):
r = np.random.permutation(len(y))
return X[r], y[r]
def _initialize_weights(self, m):
self.w1 = randn(m)
self.w2 = randn(m)
self.w3 = randn(m)
self.b = randn(1)
self.w_initialized = True
def _update_weights(self, xi, target):
output = self.activation(xi)
error = (target - output)
if self.model == 'linear':
self.w1 += self.eta * xi * error
elif self.model == 'poly2':
self.w1 += self.eta * xi * error
self.w2 += self.eta * (xi**2) * error
elif self.model == 'poly3':
self.w1 += self.eta * xi * error
self.w2 += self.eta * (xi**2) * error
self.w3 += self.eta * (xi**3) * error
self.b += self.eta * error
cost = 0.5 * error**2
return cost
def activation(self, X):
if self.model == 'linear':
return np.dot(X, self.w1) + self.b
elif self.model == 'poly2':
return np.dot(X, self.w1) + np.dot((X**2), self.w2) + self.b
elif self.model == 'poly3':
return np.dot(X, self.w1) + np.dot((X**2), self.w2) + np.dot((X**3), self.w3) + self.b
def predict(self, X):
return np.where(self.activation(X) >= 0.0, 1, -1)
import numpy as np
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier, resolution=0.02):
'''
https://github.com/rasbt/python-machine-learning-book/tree/master/code/ch02
'''
# setup marker generator and color map
markers = ('o', 's', 'x', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.9, c=cmap(idx), s=100,
edgecolor='black',
marker=markers[idx],
label=cl)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from numpy.random import *
from MyClass import MyClass
from plot_decision_regions import plot_decision_regions
# load dataset
df = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/iris/iris.data', header=None)
df.tail()
# select setosa and versicolor
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
# extract x and y
X = df.iloc[0:100, [0,1]].values
# normarize X
X_std = np.copy(X)
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()
model_names = ['linear', 'poly2', 'poly3']
for model in model_names:
# import model
ada = MyClass(n_iter=50, eta=0.01, random_state=1, model=model)
# fitting
ada.fit(X_std, y)
# predict & plot
plot_decision_regions(X_std, y, classifier=ada)
plt.title(model)
plt.xlabel('x [normarized]')
plt.ylabel('y [normarized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.savefig(model + '.png', dpi=300)
plt.show()
del ada
参考:
どやっ!