目的
データ分析・統計も学んでいます。
今回は、その中でも
母集団から取り出すサンプルサイズの大きさと効果量dについて
学んだことをアウトプット・共有します1。
WEB上にはいろいろな資料がありますが、
大事なのは、自分自身で腑に落とせるか、なので
ここでの説明で腑に落ちる人がいれば幸いです。
結論
サンプルサイズは、効果量d(=正規分布の重なり具合)をどの程度にするかで検定前に決めることができる。
これをしないと、検定の妥当性が低くなったり、過大なサンプル収集を行うリスクが出る。
中心極限定理
ある母集団から何個かのサンプルを取り出して(=抽出)、
サンプルの持つデータの平均値を計算する。
この作業を繰り返す。
横軸に平均値、
縦軸に抽出回数、
にして、データをプロットすると、正規分布になる。
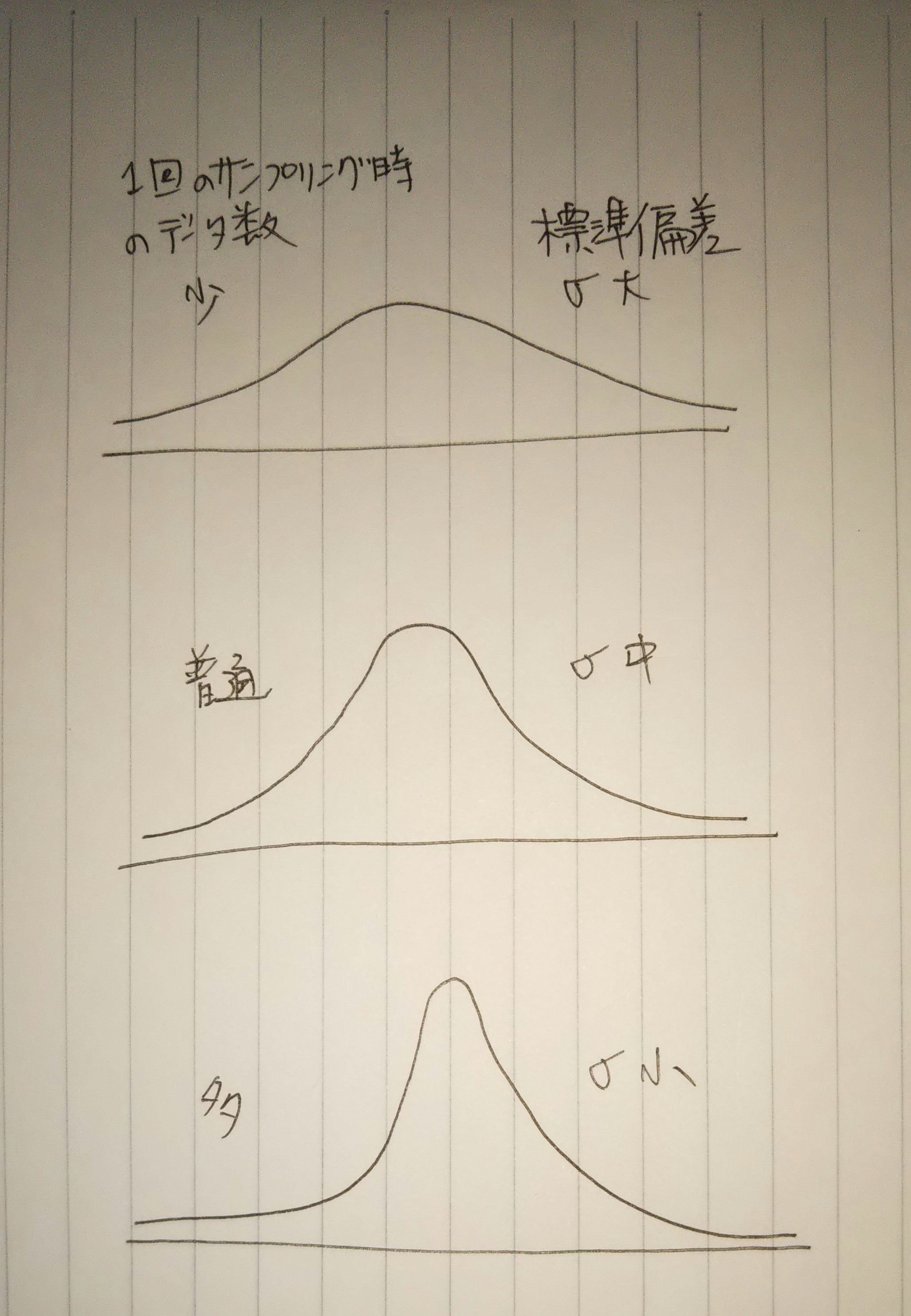
このときの正規分布のばらつき:標準偏差(σ)は1回の抽出のサンプル数が多いほど
小さくなる。
このことは、
「母集団からサンプル数を多くとればとるほど、母集団の特性(真の平均値)をより強く抽出できるよ!!」
って感じで直感的に納得できると思います2。
この考えを中心極限定理といいます。
サンプルサイズと有意性
二つのデータグループ、
A:東京都民全員
B:自分の親族30人
を考えてください。
この二つのグループの平均年齢を推定し、両グループ間に有意な差があるかを判断したいとします。つまり、自分の親族の平均年齢は諸事情で東京都都民の平均年齢とは異なる、ということを検証したいとします。
なお、このグループA,Bの平均値が完全に一致するほうが”むしろ異常”であるという直感を持っていてください。
ここで話を簡単にするために、Bグループはすでに真の平均値(全員の年齢の平均値)を
把握しているとします。この値をμB=35歳としましょう。
Aグループは母集団が大きいため、真の平均値を知ることはできません。
そのため、標本を採って真の平均値を推定するとします。
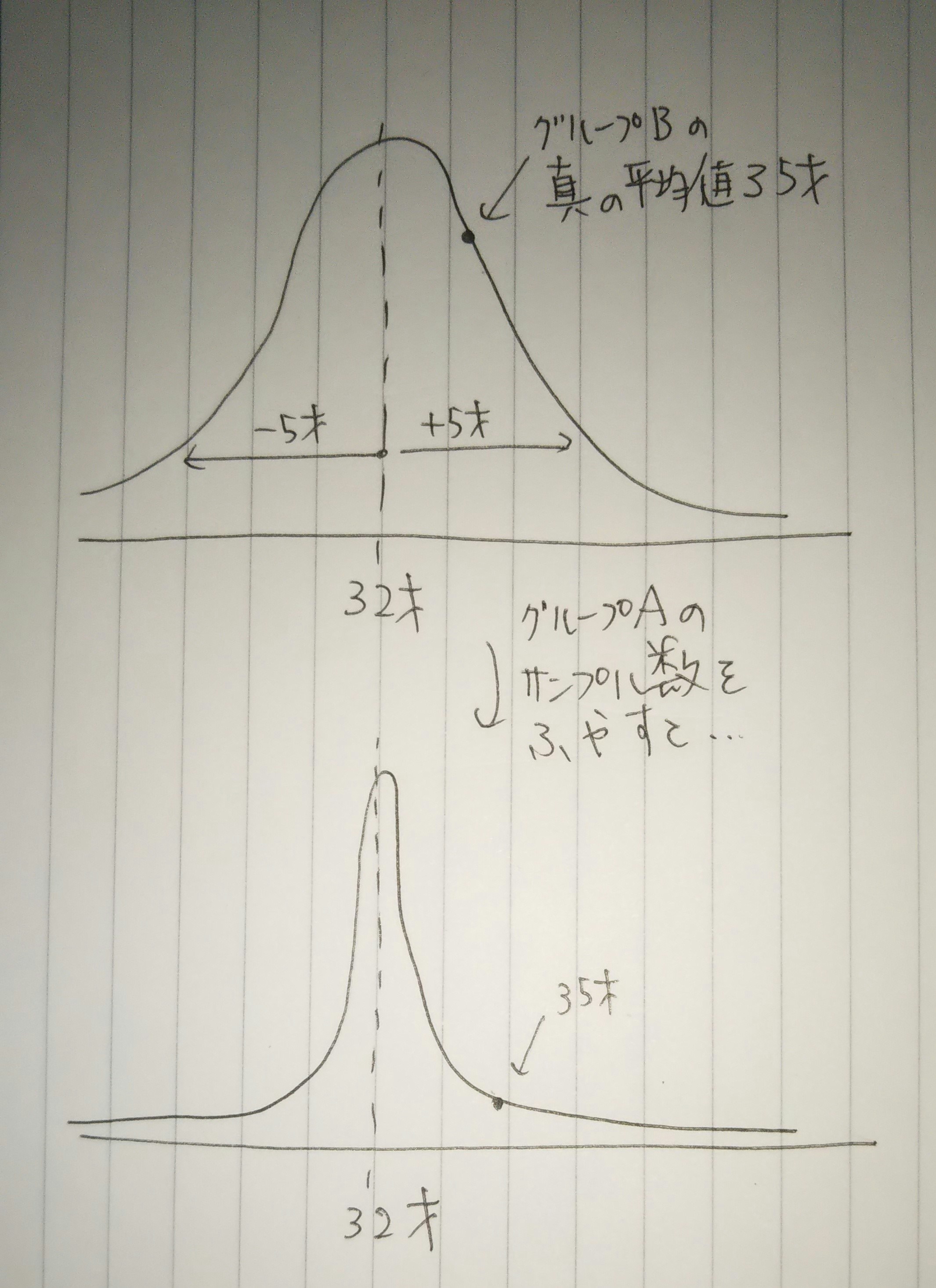
このサンプリングの結果、標準偏差σA=5歳で、μA=32歳だったとします。
(つまり、この標本はピークが32歳で、およそ±5歳のばらつきを持つ正規分布に従う)
さて、このグループの平均値の差(μAーμB)は有意なのでしょうか??
この時点では、
「有意ではない」
と判断しえるかもしれません。
なぜなら、σA=5で、μA=32の正規分布なら、μB=35は統計上の誤差といえる値だからです。
しかし、ここで、(何かの陰謀を持って)検定者が
「どうしても、この差は有意である、と言いたい!」
と強い意思をもって、作為的に「有意である」としたいと考えたら
彼は何をするでしょうか?
(有意という事柄に関しては、今回は説明を省略します)
それは
「グループAのサンプル数をできるだけ増やして、σAを小さくする」
です。
これをすると、何が起きるのでしょうか?
ここで、前節で紹介した中心極限定理が効いてきます。
中心極限定理を極端に考えると、
結局、”母集団そのもの全体”をサンプルとして取ってきて、平均を取ればσ=0となり、真の平均値を得ることになります。
これをすると、
正規分布の幅(ばらつき)が無くなります。
その結果、μBがμAと完全に一致しない限り、この平均の差は有意な差であると判断できてしまうのです。
でも、
サンプル数を増やせば、どんな平均の差も有意に持ち込める。
。。。これはおかしいですよね。
このような統計結果の作為的な操作を抑止するために導入するのが、効果量dです。
効果量d
効果量dは両グループの平均の差を、両グループの標準偏差の加重平均で割ったものです。
d=(μA-μB)/(σAとσBの加重平均) (今の場合、σBはゼロ)
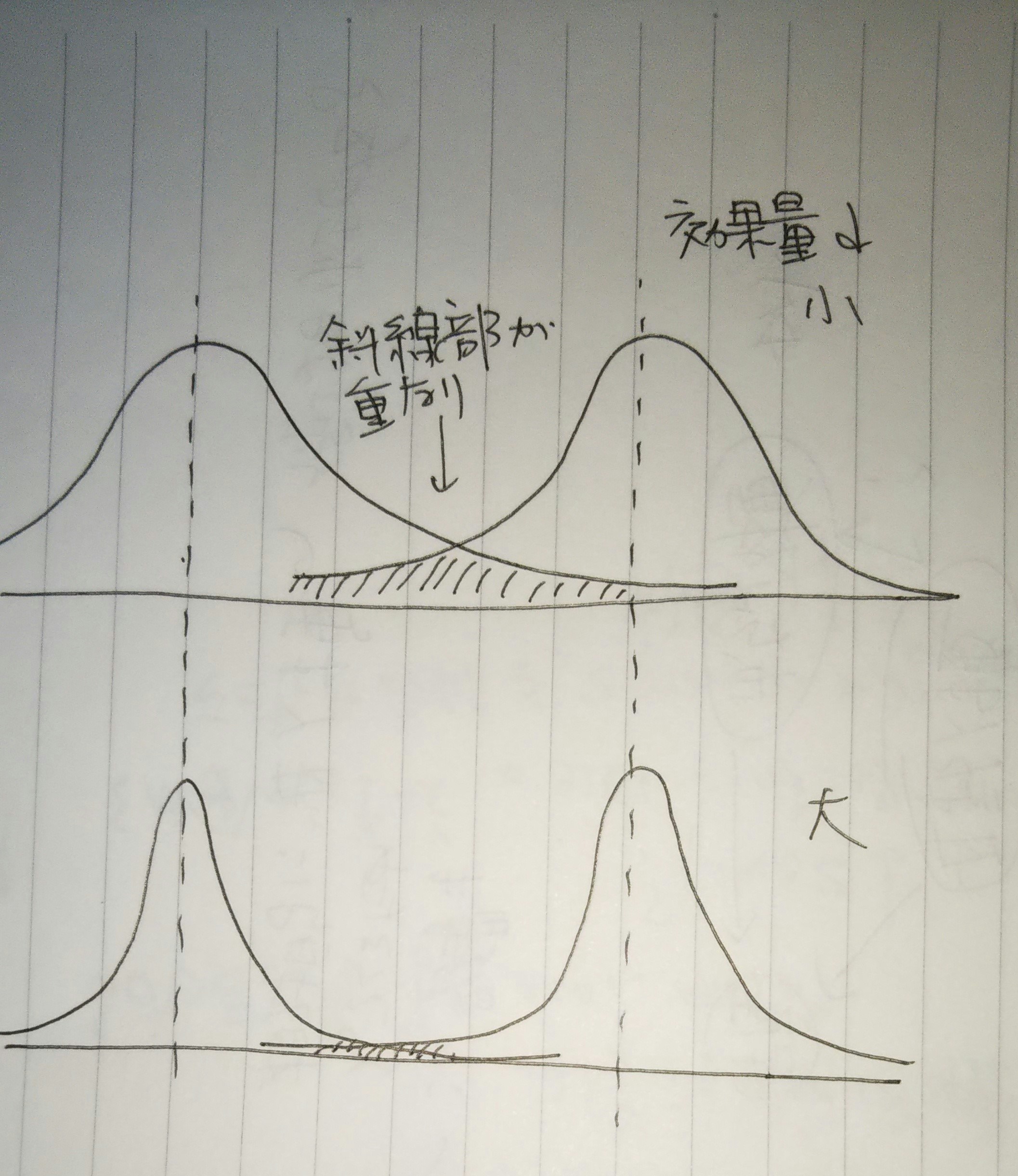
イメージとしては
二つのグループの正規分布の重なり具合を示す指標です。
dが大きいほど、重なりは小さいです。
dが小さいほど、重なりは大きいです。
以下の解釈があっているか悩み中です。ご指摘いただけると嬉しいです
Q.効果量どういった値を取ればいいのか
A.小0.2、中0.3~0.5、大0.8から取るのがいいようです。
小中大での値は分野ごとに異なるようなので、一概に「この値!」とは言えません。
また、小中大のどれを取るかも決まりはないようです。
大事なのは、おおよそこれらの値に入るように検定しなさい、ということです。
例えば効果量d=0.3を採用した場合、平均の差が3歳(=μA-μB)だった場合、標準偏差σAは10歳が必要になる計算です(3/10=0.3)。このように効果量と標準偏差を決めると、サンプルサイズを指定することになります(サンプルが少ないとσAは10歳より大きくなり、サンプルが多いと、σAは10歳より小さくなる)。
ですので、統計を行う前に、
1.効果量をおおよそ決める
2.得られるであろう平均の差を予想する
3.効果量と平均の差によって、最適なサンプル数が求まる
また、自分が当初勘違いしたこととして、
「効果量dは大きければ大きいほど良いor小さければ小さいほど良い」
という究極論発想をしていましたが、前述したように、ある程度値の間に収めることが大事です。
以下参考にした投稿
効果量とは何か
おわりに
次はR言語を使ってグラフを書きます