概要
先日は、Pythonで「母分散の推定(母平均未知)の場合」を行いました。コード的には、stats.chi2.interval 関数を用い母分散の信頼区間を求めるだけです。その引数として「信頼度:alpha」「自由度:df」を必要としました。基本は$\chi^2$値について、
$P(0.831≤χ2≤12.833)=0.95$
が成り立つため(と言いながらこういう表現は見たことがありません)、母分散の信頼区間を求めるために上手い具合に式を変形して求められるのでした。
前回の記事
統計的推定と検定をPythonで解く「母分散の推定(母平均未知)の場合」(2020.4.19)
今回は、「母平均の検定(正規母集団で母分散未知の場合)」について解いていこうと思います。今回も「とけたろうさんのチートシート」を使わせて頂きます。
問題
【問題】ある工場では,内容量20gの袋詰めされたお菓子を作っている。この工場で作られたこのお菓子を無作為に6個抽出し,開封して重さを測ったところ,標本平均と不偏分散は次のようになった。
$$\bar{X}=19.6,\ U^2=0.26$$
このお菓子の内容量は正規分布に従うものとし,その母平均を$\mu$とする。帰無仮説を$\mu=20$,対立仮説を$\mu \neq 20$,有意水準を5%として,母平均を検定しなさい。
解説
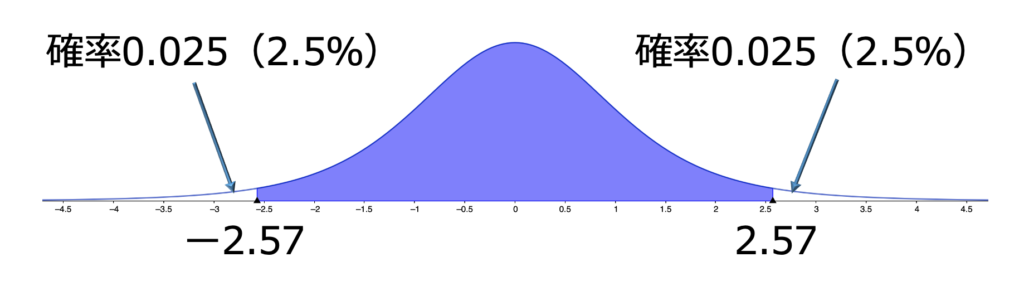
対立仮説が「$\mu \neq 20$」のように不等号で表される場合には両側検定を使います。製品の重さなどのように,それより大きくても小さくてもいけない場合に使われます。有意水準5%で両側検定を行う場合,次の図の両端の色のついていない部分のように,右すその2.5%と左すその2.5%に分け,この領域に検定量の値が入れば帰無仮説を棄却することにします。
そして,母分散が問題では与えられず,代わりに不偏分散を用いることになるので,上で説明したように,次の式で定まる$T$が検定量になります。
$$T=\frac{\bar{X}-\mu}{U}$$
いま,標本の大きさが6なので,$T$は帰無仮説のもとで自由度5の$t$分布に従います。
帰無仮説は「$\mu=20$」なので,母平均が20gであるとして検定量を計算すると,次のようになります。
$t$分布表を調べると,自由度5の$t$分布の下側2.5%点は-2.57なので,この検定量の値は棄却域には入りません。したがって,帰無仮説は棄却できません。
$$P(2.57\geqq |T|)=0.05$$
これは「6個のお菓子の平均値」は確率的にいろんな値を取り、計算される $T$ もそれに応じていろいろな値をとり標準正規分布に従います。そして、もし帰無仮説が正しい場合は$−2.776\leqq T \leqq 2.776$ の範囲内に収まります。もし左右にある、合わせて5%の棄却域に入った場合には、帰無仮説は正しくない可能性がある(ので,帰無仮説を棄却する)、という事だと理解しておきます。では $T$ とは何かというと、次の式で求められます。これを用いて「母平均が20であるかどうかの検定」を行います。これは「統計的推定と検定をPythonで解く「区間推定(正規母集団で母分散未知の場合)」でも使用しています。
$$
\begin{align}
T &= \frac{\bar{X}-\mu}{SE}\\
SE &= \sqrt{\frac{U^2}{n}}=\sqrt{\frac{0.26}{6}}≒0.21
\end{align}
$$
帰無仮説は「$\mu=20$」なので,母平均が20gであるとして検定量を計算すると,次のようになります。
$$T=\frac{19.6-20}{SE}≒-1.92$$
$t$分布表を調べると,自由度5のt分布の下側2.5%点は-2.57なので,この検定量の値は棄却域には入りません。したがって,帰無仮説は棄却できません。
ここで,注意してほしいのは,帰無仮説が棄却できなかったからと言って,帰無仮説が正しいことが立証されたわけではないということです。「棄却できなかった」というのは,「棄却できるだけの十分な結果は得られなかった」というだけです。