背景
先日は、Pythonで「区間推定(一般母集団で大標本の場合)」を行いました。コード的には、stats.binom.interval 関数を用い母比率の信頼区間を求めるだけです。その引数として「信頼度:alpha」「標本数:n」「母比率:p」を必要としました。基本は標準化得点$Z$について、
$P(−1.64≤Z≤1.64)=0.90$
が成り立つため、母比率の信比率頼区間を求めるために上手い具合に式を変形して求められるのでした。
前回の記事
統計的推定と検定をPythonで解く「区間推定(一般母集団で大標本の場合)」(2022.4.11)
今回は、「区間推定(母分散の推定で母平均未知の場合)」について解いていこうと思います。今回も「とけたろうさんのチートシート」を使わせて頂きます。
問題
あるメーカーが製造しているロープの破断荷重(ロープに物をつるしたときにロープが破損する重さ)を調べるために,6本のロープを無作為に抽出したところ,次のような結果になった。
5.1,4.7,5.3,5.2,5.5,4.8(トン)
このとき,母分散σ2の信頼度95%の信頼区間を求めなさい。ただし,メーカーが製造しているロープの破断荷重は正規分布に従うものとする。
解答
どういう問題か(問題の分類)
今回も、母分散の区間推定です。確率分布としてはカイ二乗分布で、母分散は未知です。
どのように解けるか(解法)
標本の大きさを $n$,不偏分散を$U^2$とすると,次の確率変数は自由度$(n-1)$の$\chi^2$分布に従います。
$$\frac{(n-1)U^2}{\sigma^2}$$
まず$\chi^2$(カイ二乗)値については次のようになります。
$$\chi^2=\frac{(n-1)U^2}{\sigma^2} ①$$
カイ2乗分布表から,自由度5のカイ2乗分布の下側2.5%点は0.831,上側2.5%点は12.833であるから,次の不等式が成り立ちます。
$$0.831\leq \chi^2\leq12.833$$
これに①を代入すると
$$0.831\leq \frac{(n-1)U^2}{\sigma^2}\leq12.833②$$
ここで不偏分散$U^2$の$(n-1)$倍を計算すると,次のようになります。
$5U^2$
$=(5.1-5.1)^2+(4.7-5.1)^2+(5.3-5.1)^2+(5.2-5.1)^2+(5.5-5.1)^2+(4.8-5.1)^2$
$=0.46$
②に$5U^2$を代入して、母分散について解くと次のようになります。
$$\frac{0.46}{12.833}\leq\alpha^2 \leq\frac{0.46}{0.831}$$
最左辺と最右辺を小数第4位を四捨五入して計算すると,母分散の信頼度95%の信頼区間は次のようになります。
$$0.036\leq \alpha^2 \leq 0.554$$
どのように解けるか(Python)
import numpy as np
from scipy import stats
data=np.array([5.1,4.7,5.3,5.2,5.5,4.8])
df = len(data)-1 # 自由度n-1
U5 = np.var(data, ddof=1)*df #不偏分散の自由度倍
low, high = stats.chi2.interval(alpha=0.95, df=df)
print(f"不偏分散Uの自由度({df})倍は{U5:.2f}となります。これより、")
print(f"母分散の信頼度95%の信頼区間は{U5/high:.3f}≦σ^2≦{U5/low:.3f}となります")
母分散$\sigma^2$の信頼度95%の信頼区間は
$0.036\leq \sigma^2\leq 0.553$になります。
次に、このコードの解説をしていきます。前回は 二項分布ですので stats.binom.interval 関数を使いました。今回は $\chi^2$ 分布ですので stats.chi2.interval 関数を使います。これを使うためには、「信頼度:alpha」「自由度:df」が必要になります。また、不偏分散$U$はnp.var 関数を使って求めています。
可視化
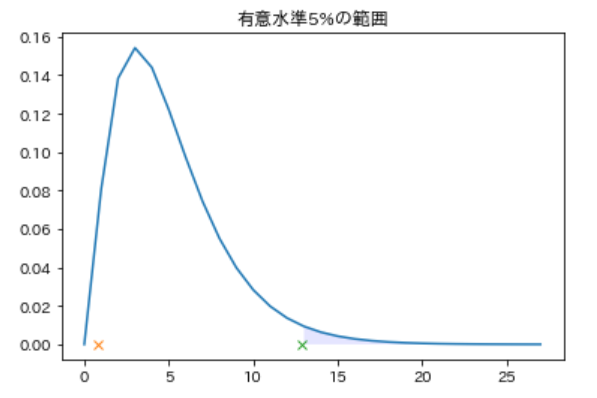
この時想定する$\chi^2$分布は次の様になります。
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
rv=stats.chi2(df=5)
x=np.arange(0,28,1)
plt.plot(x, rv.pdf(x))
plt.title(f"有意水準{(1-0.95)*100}%の範囲")
plt.fill_between(x, rv.pdf(x), where=(x>=rv.ppf(0.975)), facecolor='blue', alpha=0.1)
plt.fill_between(x, rv.pdf(x), where=(x<=rv.ppf(0.025)), facecolor='blue', alpha=0.1)
plt.plot(rv.ppf(0.025),0,marker='x')
plt.plot(rv.ppf(0.975),0,marker='x')
plt.show()
感想
- この記事を作ってみて
今回は、統計的推定の簡単な問題3です。前回の「区間推定(正規母集団で母分散未知の場合)」でした。違いは「二項分布か$\chi^2$分布か」くらいです。私の表現の仕方に癖があり、受け入れられない方も多くいらっしゃると思いますが、そこは生暖かい目で見守って頂ければと思います。また、間違いの指摘やご意見などありましたら遠慮なく仰って下さい。