はじめに
マクドナルドで購入できるラインナップの一つにフィレオフィッシュという商品がある。「外はサクサク、中はしっとりふっくらのフィッシュポーション。白身魚のおいしさを味わえる人気メニュー」ということは周知の内容かと思うが、フィレオフィッシュにまつわる都市伝説的な話があるのはご存じだろうか。
その説とは「雨が降るとフィレオフィッシュの売れ行きが良くなる」とのことである。
とあるTV番組でも取り扱ったことがあるぐらい有名な説であるらしいが、本当にそうなのか私自身気になってしまった。
今回、データ分析の力を使って、その説が本当なのか、また因果関係を証明するにはどうすればよいのかを考えてみた。
分析に用いたデータ
松江駅の人流データ(マクドナルド需要の指標として活用)
正直、扱えるデータが見つからないことに一番苦労した。
店舗でのフィレオフィッシュの売り上げ個数や利益などの公開データがあると一番良いのだが、なかなか見当たらない。
諦めきれず近しいものを探ってみたところ、、
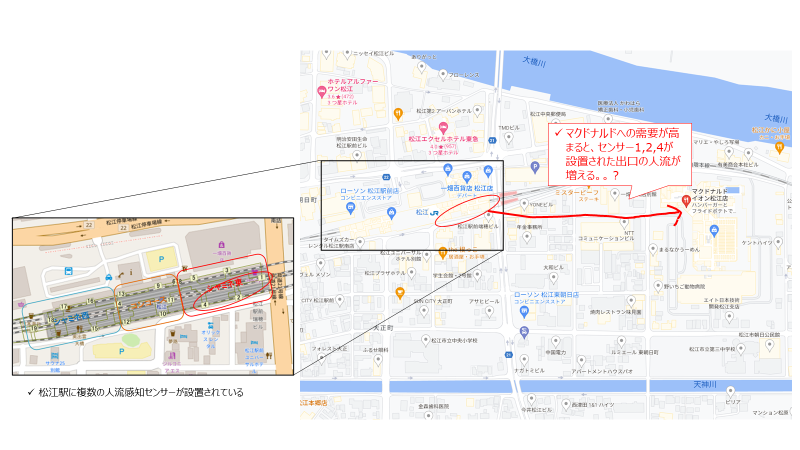
G空間情報センターwebページで公開されている島根県松江駅の人流センサデータというものがあった。松江駅構内にはセンサが19個設置されており、センサがある出入口から入ってきた人数や出ていった人数が1分毎に取得されているとのこと。
また、松江駅近郊のイオン内にマクドナルドがあるのを発見。
苦肉の策であるが、マクドナルドの需要が高まるとイオン方面の松江駅出口の人流が増え、それをセンサによって検知されるという(強引な)仮定のもと、データの解釈を行うこととした。
松江市の天候データ
天候データについては気象庁が公開している松江市の過去天候データを活用。
降雨量(mm)を天候指標として用いた。
https://www.data.jma.go.jp/gmd/risk/obsdl/index.php
分析の方針
松江駅の人流データはマクドナルドの需要を表しているとの仮定を置き、「雨が降ることで、松江駅イオン出入口の人流が増える」との因果関係の検証を行う。
利用するデータは日時毎の時系列のデータであったため、ベクトル自己回帰(VAR)モデルとグレンジャー因果性の手法を用いることにした。
VARモデルとは、ARモデルを多変量に拡張したものである。
式としては次にように表現できる。
y_t=c+\Phi_1 y_{t-1}+ \dots +\Phi_1 y_{t-1}+\epsilon_t, \epsilon_t \sim W.N.(\Sigma)
ここで、$c$はn×1定数ベクトル、$\Phi_i$はn×n係数行列。
ちなみに2変量のVAR(1)モデルは次にようになる。
\left\{ \begin{array} ~y_{1t}=c_1+\phi_{11} y_{1,t-1}+\phi_{12} y_{2,t-1}+\epsilon_{1t} \\ y_{2t}=c_2+\phi_{21} y_{1,t-1}+\phi_{22} y_{2,t-1}+\epsilon_{2t} \end{array} \right.
\left ( \begin{array} ~ \epsilon_{1t} \\ \epsilon_{2t} \end{array} \right ) \sim W.N.(\Sigma)
VARによるモデル化を行うことでグレンジャー因果、インパルス応答関数、分散分解というような時系列間の関係性を捉えることが可能になる。
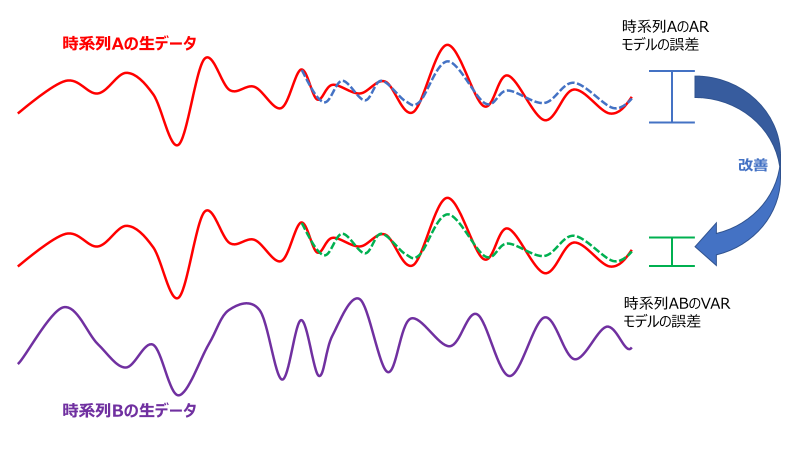
グレンジャー因果性については以下のイメージ図を参照してほしいが、
①A,Bの時系列データでVARモデルによる予測精度
②Aのみの時系列データでVARモデルによる予測精度
この時、①の方が精度が良ければ、BはAの予測精度に貢献しており関係性がある(=グレンジャー因果性あり)、というのが大筋の考え方だそうだ。
ただし、グレンジャー因果性には注意点があり
- グレンジャー因果性は通常の因果性とは異なり、通常の因果性が存在する必要条件ではあるが、十分条件ではない。
- 因果の方向が実際と真逆になることもある。そのため因果の方向がはっきりしている場合をのぞいて、定義通りに予測に優位かどうかという観点で解釈するのが良いとされている。
- 単位根過程同士から成るVARモデルに対しては、「見せかけの回帰」が起きてしまい不当な関係性を検出する恐れがある。そのため単位根ではないかを事前に検定なりでチェックを行う必要がある。
グレンジャー因果性がある=因果関係があるとは言えないことには留意する必要があるのだが、今回は降水量が上昇するのにつれてイオン方面口の人流が増加することがグレンジャー因果性で認められれば説立証とする。
分析の内容
まずは、今回扱うメインのデータとしては
- 松江駅(イオン側出入口)の人流データ
- 松江市の天候データ
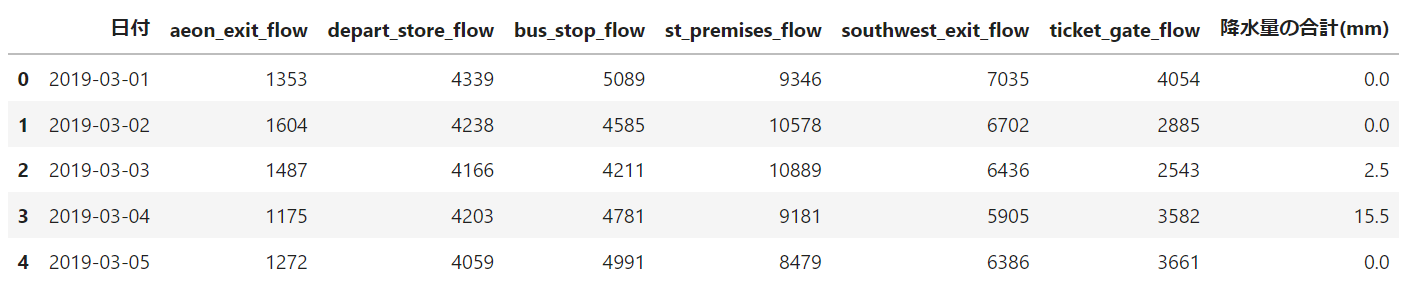
である。日付単位に加工した以下のデータフレームを用意した。
データ取得期間は19年3月~6月のコロナ過影響を避けた断面を採用した。
日付:データの取得日。日付別に丸めて処理。
aeon_exit_flow:1日のイオン側出入口から出ていった人数
depart_store_flow:1日のデパート側出入口から出ていった人数
bus_stop_flow:1日のバス乗り降り側出入口から出ていった人数
st_premises_flow:1日の駅構内連絡出入口から出ていった人数
southwest_exit_flow:1日の南西側出入口から出ていった人数
ticket_gate_flow:1日のチケット出入口から出ていった人数
降水量の合計(mm):1日の降水量(mm)
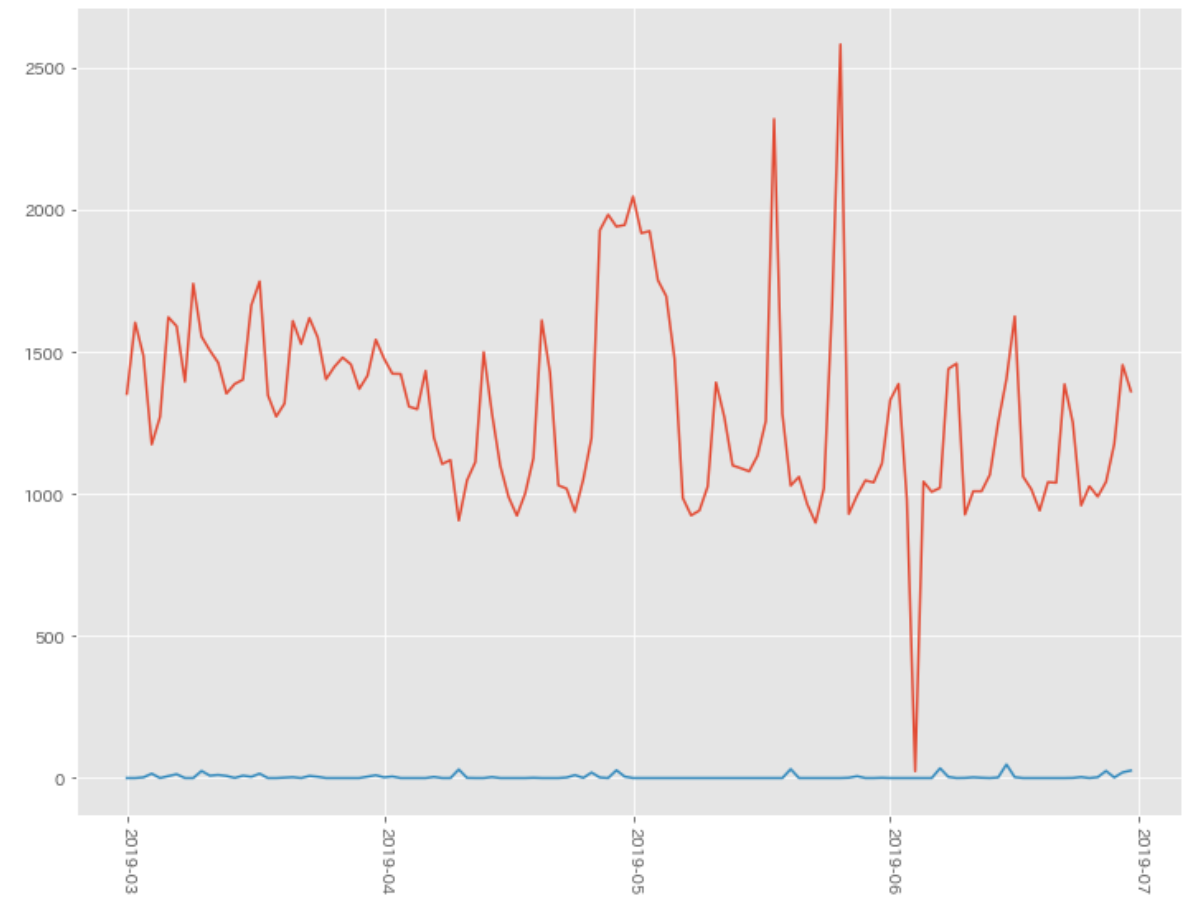
グラフ化すると以下のようになった。見たところ2つのデータ同士の関係性がないように思えるが、気にせず先に進める。
- 赤線:aeon_exit_flow:1日のイオン側出入口から出ていった人数
- 青線:降水量の合計(mm):1日の降水量(mm)
単位根検定
グレンジャー因果性には以下の性質があるため、2つの時系列データに対し、念のため単位根検定を行う。
- 単位根過程同士から成るVARモデルに対しては、「見せかけの回帰」が起きてしまい不当な関係性を検出する恐れがある。そのため単位根ではないか検定を行う必要がある。
以下の3つの対立仮説のADF単位根検定(Augmented Dickey-Fuller 単位根検定)を行う。
- 対立仮説1:定数項+トレンド+定常過程
- 対立仮説2:定数項+定常過程
- 対立仮説3:定常過程(定数項なし)
⇒帰無仮説は「単位根がある」となる。
import pandas as pd
from matplotlib import mlab
from matplotlib.dates import DateFormatter
import matplotlib.pyplot as plt
import matplotlib.dates as dates
import seaborn as sns
import datetime
import pingouin as pg
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.vector_ar.var_model import VAR
import japanize_matplotlib
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定
# Augmented Dickey-Fuller 単位根検定(帰無仮説:単位根がある)
# イオン側人流データ に対して検定
ct_results = adfuller(df['aeon_exit_flow'],regression='ct') #対立仮説:定数項+トレンド+定常過程
c_results = adfuller(df['aeon_exit_flow'],regression='c') #対立仮説:定数項+定常過程
n_results = adfuller(df['aeon_exit_flow'],regression='n') #対立仮説:定常過程(定数項なし)
# p値
print(ct_results[1])
print(c_results[1])
print(n_results[1])
> 0.0003748172114950353
> 0.01969798972873427
> 0.43618770014838654
# Augmented Dickey-Fuller 単位根検定(帰無仮説:単位根がある)
# 降水量の合計 に対して検定
ct_results = adfuller(df['降水量の合計(mm)'],regression='ct') #対立仮説:定数項+トレンド+定常過程
c_results = adfuller(df['降水量の合計(mm)'],regression='c') #対立仮説:定数項+定常過程
n_results = adfuller(df['降水量の合計(mm)'],regression='n') #対立仮説:定常過程(定数項なし)
# p値
print(ct_results[1])
print(c_results[1])
print(n_results[1])
> 8.697642968547806e-16
> 4.683663059669604e-18
> 0.0003161963698602062
どちらもp値が0.05未満で帰無仮説が棄却され、「対立仮説:定数項+トレンド+定常過程」が選択されているので問題なさそう。
VARモデル構築
次にVARモデルの構築を行う。
# データフレームを配列へ変換
x = df[['aeon_exit_flow', '降水量の合計(mm)']].to_numpy()
# 最大のラグ数
maxlags = 10
# モデルのインスタンス生成
model = VAR(x)
# 最適なラグの探索
lag = model.select_order(maxlags).selected_orders
print('最適なラグ:',lag['aic'],'\n')
# モデルの学習
results = model.fit(lag['aic'])
print(results.summary())
最適なラグ: 9
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Sat, 10, Dec, 2022
Time: 17:52:58
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: 16.5957
Nobs: 113.000 HQIC: 16.0507
Log likelihood: -1168.52 FPE: 6.48500e+06
AIC: 15.6786 Det(Omega_mle): 4.75247e+06
--------------------------------------------------------------------
Results for equation y1
========================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------
const 540.403167 165.525564 3.265 0.001
L1.y1 0.472030 0.092044 5.128 0.000
L1.y2 5.283509 3.099986 1.704 0.088
L2.y1 0.061483 0.102556 0.600 0.549
L2.y2 0.358304 3.157396 0.113 0.910
L3.y1 0.061519 0.102364 0.601 0.548
L3.y2 2.395330 3.136938 0.764 0.445
L4.y1 -0.037511 0.103448 -0.363 0.717
L4.y2 1.656983 3.255675 0.509 0.611
L5.y1 -0.098889 0.102891 -0.961 0.337
L5.y2 3.247523 3.231158 1.005 0.315
L6.y1 0.149669 0.103988 1.439 0.150
L6.y2 2.678368 3.232657 0.829 0.407
L7.y1 0.197687 0.104756 1.887 0.059
L7.y2 -1.164727 3.147883 -0.370 0.711
L8.y1 0.196532 0.106744 1.841 0.066
L8.y2 -2.697325 3.144779 -0.858 0.391
L9.y1 -0.445299 0.092488 -4.815 0.000
L9.y2 -3.127205 3.169940 -0.987 0.324
========================================================================
Results for equation y2
========================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------
const 9.517614 5.655992 1.683 0.092
L1.y1 0.001156 0.003145 0.368 0.713
L1.y2 0.071127 0.105926 0.671 0.502
L2.y1 0.006511 0.003504 1.858 0.063
L2.y2 -0.048286 0.107888 -0.448 0.654
L3.y1 -0.008941 0.003498 -2.556 0.011
L3.y2 0.094248 0.107189 0.879 0.379
L4.y1 0.002555 0.003535 0.723 0.470
L4.y2 -0.050219 0.111246 -0.451 0.652
L5.y1 -0.004135 0.003516 -1.176 0.240
L5.y2 -0.072729 0.110408 -0.659 0.510
L6.y1 0.003557 0.003553 1.001 0.317
L6.y2 -0.045164 0.110460 -0.409 0.683
L7.y1 -0.001262 0.003580 -0.353 0.724
L7.y2 -0.057694 0.107563 -0.536 0.592
L8.y1 -0.001490 0.003647 -0.409 0.683
L8.y2 0.141916 0.107457 1.321 0.187
L9.y1 -0.002189 0.003160 -0.693 0.489
L9.y2 -0.041442 0.108317 -0.383 0.702
========================================================================
Correlation matrix of residuals
y1 y2
y1 1.000000 0.011857
y2 0.011857 1.000000
グレンジャー因果性の検定
「イオン口人流 → 降水量」と「降水量 → イオン口人流」についてグレンジャー因果性の検定を行う。
帰無仮説:グレンジャー因果性がない
対立仮説:グレンジャー因果性がある
⇒p値が0.05未満のとき帰無仮説が棄却されたと考え対立仮説を採択する。
# イオン口人流 -> 降水量 のグレンジャー因果性を検定
test_results = results.test_causality(causing=0, caused=1)
test_results.pvalue
> 0.24607473834483592
# 降水量 -> イオン口人流 の因果を検定
test_results = results.test_causality(causing=1, caused=0)
test_results.pvalue #p値
> 0.6369977231268573
どちらもp値>0.05のため帰無仮説を棄却できず、降水量とイオン口人流データには関係性が見いだせなかったこととなる。
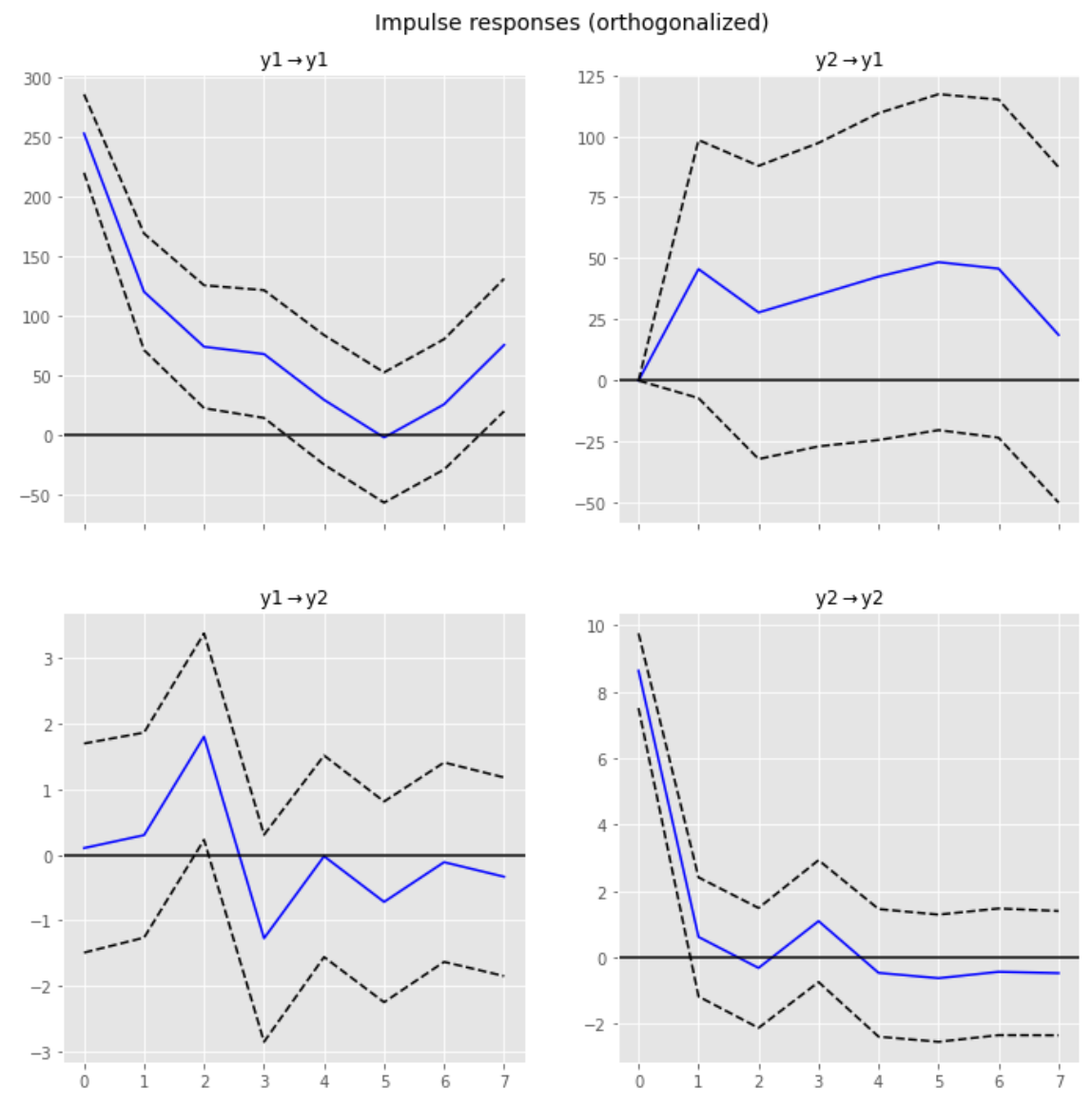
インパルス応答分析
念のためインパルス応答分析も行ってみた。
「ある時系列の変数Xに変動があったとき、他の時系列の変数Yにどう伝わっていくかをモデリング」した「直交化インパルス応答関数」を求めグラフ化し確認することで2つの時系列データの関係性を伺うことができる。
# (直行化)インパルス応答関数
period = 7
irf = results.irf(period)
irf.plot(orth=True)
plt.show()
最後に
今回の分析ではフィレオフィッシュと雨との関係性を見出すことはできなかった。
フィレオフィッシュの売り上げデータが取得できなかったのが大きな原因かと思うが、日単位では粒度が荒く、時間単位等で同様の検証を行うと結果が変わったかもしれない。時間があれば今度試してみることとする。
参照
https://www.ssnp.co.jp/foodservice/201190/
https://www.mcdonalds.co.jp/products/1110/
https://www.salesanalytics.co.jp/datascience/datascience115/
https://tjo.hatenablog.com/entry/2015/08/06/190000
https://tjo.hatenablog.com/entry/2020/11/27/180000
https://qiita.com/saltcooky/items/2d0119ea4a10bab6cff2