はじめに
これからVARモデルを利用することもあるかもしれないので、まとめてみました。(本当に個人的なまとめです)
スパース性を加えたsparse VARモデルも気になるので、そちらについても調べてみました。⇨結局この記事では扱わなかった。
基本的には、沖田先生の「計量時系列分析」と馬場さんの「時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装」を参考にしました。
VARモデル
ベクトル自己回帰(VAR)モデルは、自己回帰(AR)モデルを多変量に拡張したものです。
VARモデルを用いる目的としては、複数の変数を用いることで予測精度の向上が見込まれます。
変数間の関係の分析に関して、グレンジャー因果、インパルス応答関数、分散分解というようなツールが提供できる。
弱定常ベクトル過程
対象とする系列のn×1列ベクトル$y_t=(y_{1t},y_{2t},\dots,y_{nt})^t$とする。
このベクトル$y$の期待値(ベクトル)は次のように定義できます。
E(y_t)=[E(y_{1t}),\dots,E(y_{nt})]^t
k次の自己共分散行列は次にように$(i,j)$成分が$y_{it}$と$y_{j,t-k}$の共分散に等しい$n×n$行列になります。
Cov(y_t,y_{t-k})=[Cov(y_{it},y_{i,j-k})]_{ij}=
\left( \begin{matrix} Cov(y_{1t},y_{1,t-k}) & \ldots & Cov(y_{1t},y_{n,t-k}) \\ \vdots & \ddots & \vdots \\ Cov(y_{nt},y_{1,t-k}) & \ldots & Cov(y_{nt},y_{n,t-k}) \end{matrix} \right)
このとき、k次自己共分散行列の対角成分は、各変数のk次自己共分散に等しいです。
一般的に、期待値と自己共分散関数が$t$の関数であるが、1変数の場合と同様に、期待値と自己共分散関数が$t$に依存したしないとき、ベクトル過程は弱定常(共分散定常)と言われています。
k次の自己共分散行列を基準化したk次の自己相関行列は次にように定義できます。
\rho_k = Corr(y_{t},y_{j-k})=[Corr(y_{it},y_{i,j-k})]_{ij}
1変量時系列モデルのホワイトノイズをベクトルに拡張したベクトルホワイトノイズは、次の条件を満たす$\epsilon_t$と表現できる。
E(\epsilon_t)=0
E(\epsilon_t \epsilon_{t-k}^t) = \left\{
\begin{array}{ll}
\Sigma & (k = 0) \\
0 & (k \neq 0)
\end{array}
\right.
ここで、$\Sigma$は$n×n$手入れ一行列である、対角行列である必要はないです。
ホワイトベクトルノイズは弱定常であり、自己相関を持たないです。
$\epsilon_t$は異時点においてはどの成分も相関を持たないが、どう時点においては各成分は相関を持っても良いです。
また、$\epsilon_t$が分散共分散行列$\Sigma$のベクトルホワイトノイズであることを$\epsilon_t \sim W.N.(\Sigma)$と表記することがあります。
VARモデル
VARモデルは次にように表現できます。
y_t=c+\Phi_1 y_{t-1}+ \dots +\Phi_1 y_{t-1}+\epsilon_t, \epsilon_t \sim W.N.(\Sigma)
ここで、$c$はn×1定数ベクトル、$\Phi_i$はn×n係数行列です。
2変量のVAR(1)モデルは次にようになります。
\left\{ \begin{array} ~y_{1t}=c_1+\phi_{11} y_{1,t-1}+\phi_{12} y_{2,t-1}+\epsilon_{1t} \\ y_{2t}=c_2+\phi_{21} y_{1,t-1}+\phi_{22} y_{2,t-1}+\epsilon_{2t} \end{array} \right.
\left ( \begin{array} ~ \epsilon_{1t} \\ \epsilon_{2t} \end{array} \right ) \sim W.N.(\Sigma)
なお、n変量VAR(p)モデルは合計$n(np+1)+n(n+1)/2$のパラメータを持ちます。
VARモデルのAR多項式の行列を0とおいた次のAR特性方程式の全ての解の絶対値が1より大きいことがVARモデルの定常条件となります。
|I_n - \Phi_1 z- \dots - \Phi_p z^p|=0
ここで、$I_n$はn×nの単位行列です。
VARモデルの推定
VARモデルは各方程式に同時点の他の変数を含まない同時方程式モデルではないです。
ただし、各方程式は誤差項の相関で関係しています。
このようなモデルは、見かけ上無関係な回帰(SUR:simulataneous equation model)モデルと呼ばれています。
通常、SURモデルは誤差項の相関部分を考慮に入れた推定を行わないといけないいけません。
しかし、VARモデルにおいては全ての回帰式は同一の説明変数が含まれるため、それぞれの回帰式においてOLSで係数の推定を行えば良いです。
グレンジャー因果
変数間の因果の判別は非常に難しい問題ですが、グレンジャー因果性ではデータのみから因果性の判断を行うことができることが特徴です。
基本的な考え方は、時系列$y_t$の予測において、時系列$x_t$を用いると予測精度が向上した場合、$x_t$から$y_t$への因果性があるという考え方です。
グレンジャー因果性と一般的なグレンジャー因果性は次のように定義されます。
定義:グレンジャー因果性
現在と過去の$x$の値だけに基づいた将来の$x$の予測と、現在と過去の$x$と$y$の値に基づいた将来の$x$の予測を比較して、後者のMSEの方が小さくなる場合、$y_t$から$x_t$へのグレンジャー因果性(Granger causality)が存在するといわれる。
定義:一般的なグレンジャー因果性
xtとytをベクトル過程とする。また、xとyの現在と過去の値を含む、時点tにおいて利用可能な情報の集合をΩtとし、Ωtから現在と過去のyを取り除いたものをΩ̃ とする。このとき、Ω̃ tに基づいた将来のxの予測と、Ωtに基づいた将来のxの予測を比較して、後者のMSEのほうが小さくなる場合、ytからxtへのグレンジャー因果性が存在するといわれる。ここで、MSEの大小は行列の意味での大小であることに注意されたい。
ここで、2変量VAR(2)モデルについて考えます。
\left\{ \begin{array} ~y_{1t}=c_1+\phi_{11}^{(1)} y_{1,t-1}+\phi_{12}^{(1)} y_{2,t-1}+\phi_{11}^{(2)} y_{1,t-2}+\phi_{12}^{(2)} y_{2,t-2}+\epsilon_{1t} \\
y_{2t}=c_2+\phi_{21}^{(1)} y_{1,t-1}+\phi_{22}^{(1)} y_{2,t-1}+\phi_{21}^{(2)} y_{1,t-2}+\phi_{22}^{(2)} y_{2,t-2}+\epsilon_{2t} \end{array} \right.
この時、$y_{2t}$から$y_{1t}$へのグレンジャー因果性が存在している場合、$\phi_{12}^{(1)}=\phi_{12}^{(2)}=0$と同値になります。
逆にグレンジャー因果性がない場合は、係数が全て0であると同値になります。
そのため、グレンジャー因果性を検定するためには,F検定を用いて$\phi_{12}^{(1)}=\phi_{12}^{(2)}=0$を検定し求めていきます。
はじめに、VARモデルにおける$y_kt$のモデルをOLSで推定し、その残差平方を$SSR_1$とします。
次に、VARモデルにおける$y_kt$のモデルに制約を貸したモデルをOLSで推定し、その残差平方を$SSR_0$とします。
F統計量を次のように算出します。
F=\frac{(SSR_0-SSR_1)/r}{SSR_1/(T-np-1)}
ここで,$r$はグレンジャー因果性検定に必要な制約数です。
そして、$rF$を$\chi^2(r)$の95%店と比較し、$rF$の方が大きければ、ある変数群からの$y_{kt}$へのグレンジャー因果性は存在し、小さければグレンジャー因果性は存在しないと結論付けることができます。
グレンジャー因果性の短所としては、まずグレンジャー因果性は通常の因果性とは異なる。
グレンジャー因果性は通常の因果性が存在する必要条件ではあるが、十分条件ではない。
また、因果の方向が実際と真逆になることもある。そのため因果の方向がはっきりしている場合をのぞいて、定義通りに予測に優位かどうかという観点で解釈するのが良いとされている。
インパルス応答関数
ある変数時系列の変化がその変数時系列やその他の変数時系列に与える影響を分析することができるのが、インパルス応答関数です。
変化の識別の仕方によって、複数のインパルス応答関数が存在する。テキストでは、直行化インパルス応答関数と非直行化インパルス応答関数が紹介されています。
一般的な$n$変数VAR(p)モデルを考えます。
y_t=c+\Phi_1 y_{t-1}+ \dots +\Phi_1 y_{t-1}+\epsilon_t, \epsilon_t \sim W.N.(\Sigma)
この時の非直交化インパルス応答関数は次のように定義されます。
定義(非直交化インパルス応答関数)
$y_{jt}$の撹乱項$\epsilon_{jt}$だけに1単位(または1標準偏差)のショックを与えたときの$y_{i,t+k}$の変化は、$y_j$のショックに対する$y_i$の$k$期後の非直交化インパルス応答と呼ばれる。また、それを$k$の関数としてみたものは、$y_j$のショックに対する$y_i$の非直交化インパルス応答関数といわれる。
定義(直交化インパルス応答関数)
撹乱項の分散共分散行列の三角分解を用いて、撹乱項を互いに相関する部分と無相関な部分に分解したとき、無相関な部分は直交化撹乱項といわれる。また、$y_j$の直交化撹乱項に1単位または1標準偏差のショックを与えたときの$y_i$の直交化インパルス応答を時間の関数としてみたものは、$y_j$に対する$y_i$の直交化インパルス応答関数といわれる。
非直交化インパルス応答関数
数学的には、次にように非直交化インパルス応答関数は偏微分を用いて表現することができます。
IRF_{ij}(k) = \frac{\partial y_{1,t+k}}{\partial \epsilon_{1t}}, k=0,1,2,\dots
ここでインパルス応答分析では、偏微分表現で$y$や$\epsilon$を確率変数として扱わず、$\epsilon$の確定的な変化に対する$y$の確定的は変化を調べることになります。
非直交化インパルス応答関数は、$k=0$から逐次的に計算していくことで推定することができます。
例えば、上記の2変量VAR(1)モデルはにおいて、$y_1$に1単位のショックを与えた時の非直交化インパルス応答関数は次のように計算できます。
IRF_{11}(0) = \frac{\partial y_{1t}}{\partial \epsilon_{1t}}=1
IRF_{21}(0) = \frac{\partial y_{2t}}{\partial \epsilon_{1t}}=0
次に、$y_1$の1期後の非直交化インパルス応答は次にようになります。
IRF_{11}(1) = \frac{\partial y_{1,t+1}}{\partial \epsilon_{1t}} = \phi_{11} \frac{\partial y_{1t}}{\partial \epsilon_{1t}} + \phi_{12}\frac{\partial y_{2t}}{\partial \epsilon_{1t}}
このような計算を逐次的に繰り返すことにより、$k=1,2,\dots$において、次のような関係が得られます。
IRF_{11}(k) = \phi_{11} IRF_{11}(k-1) + \phi_{12}IRF_{21}(k-1)
これは、$y_2$においても同様に得られます。
直交化インパルス応答関数
非直交化インパルス応答関数は、撹乱項間の相関を無視していることが問題に挙げられている。
この問題を解決する方法として、なんらかの仮定をおいて錯乱項を互いに無相関な錯乱項に分解する方法が挙げられます。
直交化インパルス応答関数は錯乱項の分散共分散行列$\Sigma$を三角分解を用いて分解します。
直交化インパルス応答関数の撹乱項$\epsilon_t$の分散共分散行列$\Sigma$は、正定値行列であり次のように三角分解ができます。
\Sigma=ADA'
ここで、$A$は対角要素が1である下三角行列とDを対角行列となります。
また、直交化錯乱項$u_t$は次のように定義される。各変数固有の変動を表すとみなすことができます。
u_t=A^{-1}\epsilon_t
なお、$u_t$は互いに無相関です。
$y_j$のショックに対する$y_i$のインパルス応答関数は、$u_{jt}$に1単位のショックを与えたときのyiの反応を時間の関数としたものであり、次のように定義されます。
IRF_{ij}(k)=\frac{\partial y_{i,t+k}}{\partial u_{jt}}, k=0,1,2,⋯
1単位ではなく1標準偏差のショックを与えたいときは、上の式にそのまま${Var(u_{jt})}^{1/2}$を掛ければ良いです。
1標準偏差のショックを与えた時のインパルス応答関数を求めるためには、三角分解の代わりにコレスキー分解を用いて錯乱項を分解し、その分解した錯乱項に1単位のショックを与えて、インパルス応答関数を計算しても良いです。
$D^{1/2}$を(i,j)成分が$u_{i,j}$の標準偏差に等しい対角行列であるとすると、上記で示した$\Sigma$は$P=AD^{1/2}$として、次のように書ける。
\Sigma = AD^{1/2}D^{1/2}A'=PP'
ここで、$\Sigma$のコレスキー分解担っておりPはコレスキー因子と呼ばれます。
この$P$を用いて、錯乱項は次のように分解できる。
v_t=P^{-1}\epsilon_t=D^{-1/2}A^{-1}\epsilon_t=D^{-1/2}u_t
これは、$v_{jt}$は$u_{jt}$をその標準偏差$Var(u_{jt})^{1/2}$で割ったものになっています。
$v_{jt}$における1単位の増加が$u_{jt}$における1標準偏差の増加に等しいということを意味しています。
$v_{jt}$に1単位のショックを与えて計算したインパルス応答関数は、$u_{jt}$に1標準偏差のショックを与えて計算したインパルス応答関数に等しくなります。
RでVARモデル
RはVARモデルはvarsパッケージで実装が可能です。
今回用いるデータはvarsパッケージにあるCanadaデータセットを利用します。
このデータは1980~2000年におけるカナダの主要な4種類の経済指数で、変数変換が行われています。
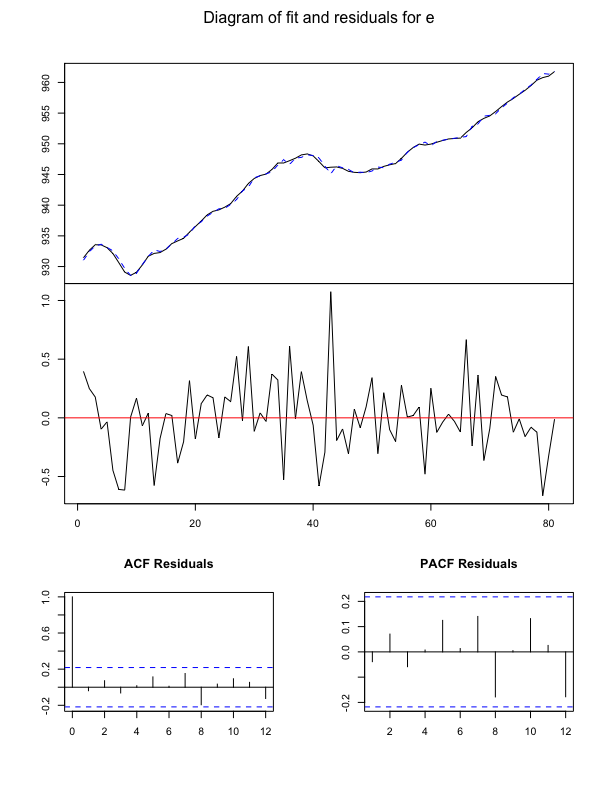
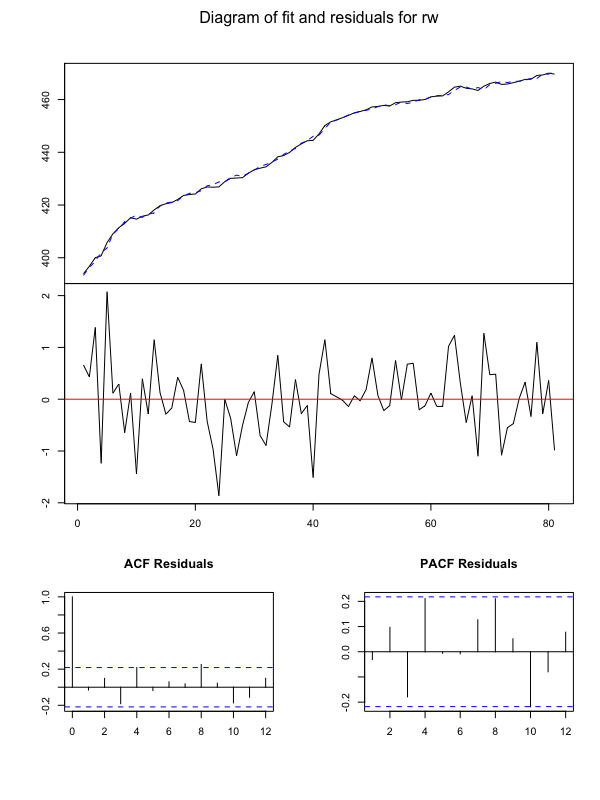
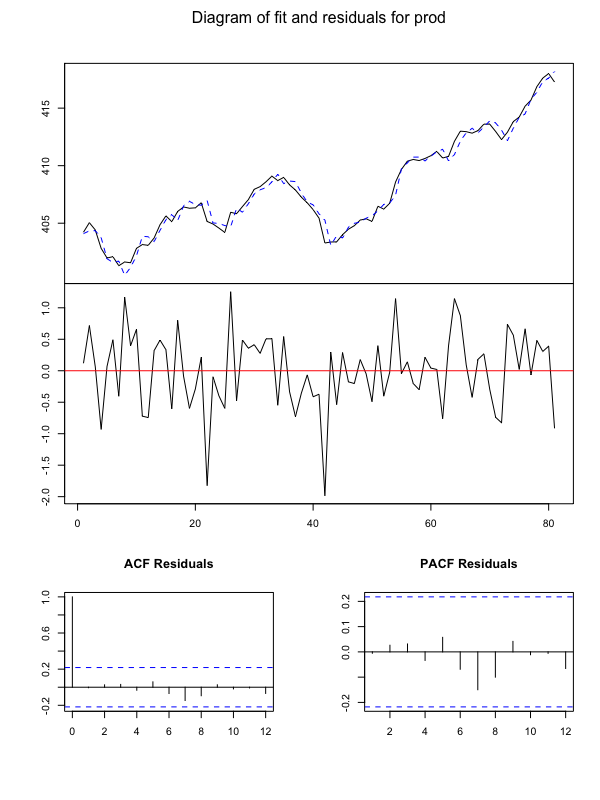
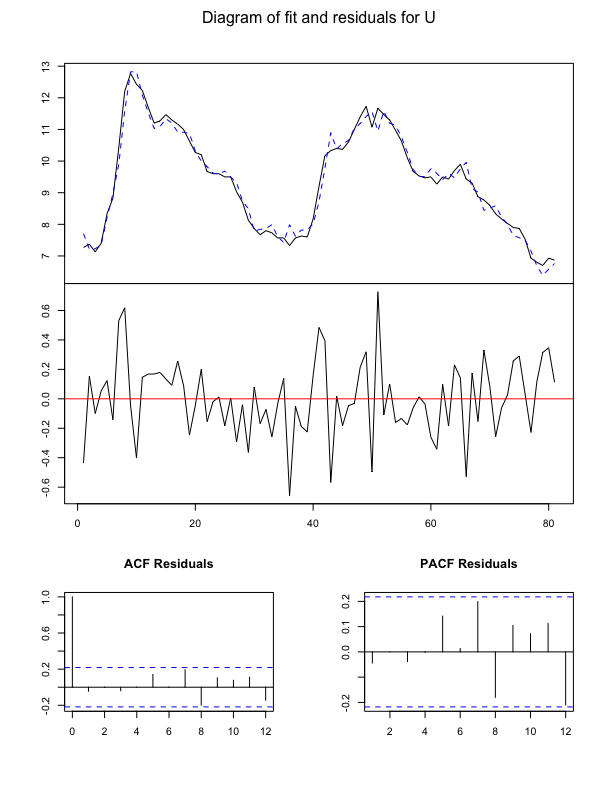
eが雇用、rwが実質賃金、prodが労働生産性、Uが失業率を表しています。
library(vars)
# データ読み込み
data(Canada)
> summary(Canada)
e prod rw U
Min. :928.6 Min. :401.3 Min. :386.1 Min. : 6.700
1st Qu.:935.4 1st Qu.:404.8 1st Qu.:423.9 1st Qu.: 7.782
Median :946.0 Median :406.5 Median :444.4 Median : 9.450
Mean :944.3 Mean :407.8 Mean :440.8 Mean : 9.321
3rd Qu.:950.0 3rd Qu.:410.7 3rd Qu.:461.1 3rd Qu.:10.607
Max. :961.8 Max. :418.0 Max. :470.0 Max. :12.770
最適なラグを推定するためにモデル選択をします。
varsパッケージではVARselect関数で推定します。
> VARselect(Canada,lag.max=6)
$selection
AIC(n) HQ(n) SC(n) FPE(n)
3 2 2 3
$criteria
1 2 3 4 5 6
AIC(n) -5.832203860 -6.341153584 -6.440077215 -6.228986742 -6.021458099 -5.89342928
HQ(n) -5.590297749 -5.905722585 -5.811121327 -5.406505966 -5.005452434 -4.68389873
SC(n) -5.227919545 -5.253441818 -4.868937997 -4.174420073 -3.483463978 -2.87200771
FPE(n) 0.002933674 0.001769561 0.001616452 0.002028286 0.002561839 0.00302821
どうやらラグは3が良さそうです。
ラグが3の場合のモデルを推定します。
# VARモデルの推定
Canada_var <- VAR(Canada,p=VARselect(Canada,lag.max=4)$selection[1])
結果を確認してみましょう。
> #結果の表示
> summary(Canada_var)
VAR Estimation Results:
=========================
Endogenous variables: e, prod, rw, U
Deterministic variables: const
Sample size: 81
Log Likelihood: -150.609
Roots of the characteristic polynomial:
1.004 0.9283 0.9283 0.7437 0.7437 0.6043 0.6043 0.5355 0.5355 0.2258 0.2258 0.1607
Call:
VAR(y = Canada, p = VARselect(Canada, lag.max = 4)$selection[1])
Estimation results for equation e:
==================================
e = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const
Estimate Std. Error t value Pr(>|t|)
e.l1 1.75274 0.15082 11.622 < 2e-16 ***
prod.l1 0.16962 0.06228 2.723 0.008204 **
rw.l1 -0.08260 0.05277 -1.565 0.122180
U.l1 0.09952 0.19747 0.504 0.615915
e.l2 -1.18385 0.23517 -5.034 3.75e-06 ***
prod.l2 -0.10574 0.09425 -1.122 0.265858
rw.l2 -0.02439 0.06957 -0.351 0.727032
U.l2 -0.05077 0.24534 -0.207 0.836667
e.l3 0.58725 0.16431 3.574 0.000652 ***
prod.l3 0.01054 0.06384 0.165 0.869371
rw.l3 0.03824 0.05365 0.713 0.478450
U.l3 0.34139 0.20530 1.663 0.100938
const -150.68737 61.00889 -2.470 0.016029 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3399 on 68 degrees of freedom
Multiple R-Squared: 0.9988, Adjusted R-squared: 0.9985
F-statistic: 4554 on 12 and 68 DF, p-value: < 2.2e-16
Estimation results for equation prod:
=====================================
prod = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const
Estimate Std. Error t value Pr(>|t|)
e.l1 -0.14880 0.28913 -0.515 0.6085
prod.l1 1.14799 0.11940 9.615 2.65e-14 ***
rw.l1 0.02359 0.10117 0.233 0.8163
U.l1 -0.65814 0.37857 -1.739 0.0866 .
e.l2 -0.18165 0.45083 -0.403 0.6883
prod.l2 -0.19627 0.18069 -1.086 0.2812
rw.l2 -0.20337 0.13337 -1.525 0.1319
U.l2 0.82237 0.47034 1.748 0.0849 .
e.l3 0.57495 0.31499 1.825 0.0723 .
prod.l3 0.04415 0.12239 0.361 0.7194
rw.l3 0.09337 0.10285 0.908 0.3672
U.l3 0.40078 0.39357 1.018 0.3121
const -195.86985 116.95813 -1.675 0.0986 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.6515 on 68 degrees of freedom
Multiple R-Squared: 0.98, Adjusted R-squared: 0.9765
F-statistic: 277.5 on 12 and 68 DF, p-value: < 2.2e-16
Estimation results for equation rw:
===================================
rw = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const
Estimate Std. Error t value Pr(>|t|)
e.l1 -4.716e-01 3.373e-01 -1.398 0.167
prod.l1 -6.500e-02 1.393e-01 -0.467 0.642
rw.l1 9.091e-01 1.180e-01 7.702 7.63e-11 ***
U.l1 -7.941e-04 4.417e-01 -0.002 0.999
e.l2 6.667e-01 5.260e-01 1.268 0.209
prod.l2 -2.164e-01 2.108e-01 -1.027 0.308
rw.l2 -1.457e-01 1.556e-01 -0.936 0.353
U.l2 -3.014e-01 5.487e-01 -0.549 0.585
e.l3 -1.289e-01 3.675e-01 -0.351 0.727
prod.l3 2.140e-01 1.428e-01 1.498 0.139
rw.l3 1.902e-01 1.200e-01 1.585 0.118
U.l3 1.506e-01 4.592e-01 0.328 0.744
const -1.167e+01 1.365e+02 -0.086 0.932
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7601 on 68 degrees of freedom
Multiple R-Squared: 0.9989, Adjusted R-squared: 0.9987
F-statistic: 5239 on 12 and 68 DF, p-value: < 2.2e-16
Estimation results for equation U:
==================================
U = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const
Estimate Std. Error t value Pr(>|t|)
e.l1 -0.61773 0.12508 -4.939 5.39e-06 ***
prod.l1 -0.09778 0.05165 -1.893 0.062614 .
rw.l1 0.01455 0.04377 0.332 0.740601
U.l1 0.65976 0.16378 4.028 0.000144 ***
e.l2 0.51811 0.19504 2.656 0.009830 **
prod.l2 0.08799 0.07817 1.126 0.264279
rw.l2 0.06993 0.05770 1.212 0.229700
U.l2 -0.08099 0.20348 -0.398 0.691865
e.l3 -0.03006 0.13627 -0.221 0.826069
prod.l3 -0.01092 0.05295 -0.206 0.837180
rw.l3 -0.03909 0.04450 -0.879 0.382733
U.l3 0.06684 0.17027 0.393 0.695858
const 114.36732 50.59802 2.260 0.027008 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2819 on 68 degrees of freedom
Multiple R-Squared: 0.9736, Adjusted R-squared: 0.969
F-statistic: 209.2 on 12 and 68 DF, p-value: < 2.2e-16
Covariance matrix of residuals:
e prod rw U
e 0.11550 -0.03161 -0.03681 -0.07034
prod -0.03161 0.42449 0.05589 0.01494
rw -0.03681 0.05589 0.57780 0.03660
U -0.07034 0.01494 0.03660 0.07945
Correlation matrix of residuals:
e prod rw U
e 1.0000 -0.14276 -0.1425 -0.73426
prod -0.1428 1.00000 0.1129 0.08136
rw -0.1425 0.11286 1.0000 0.17084
U -0.7343 0.08136 0.1708 1.00000
結果をグラフ化して確認します。
plot(Canada_var)
Rでグランジャー因果推定
varsパッケージのcausality関数により検定できます。
> #グレンジャー因果
> causality(Canada_var,cause="U")
$Granger
Granger causality H0: U do not Granger-cause e prod rw
data: VAR object Canada_var
F-Test = 2.0635, df1 = 9, df2 = 272, p-value = 0.03299
$Instant
H0: No instantaneous causality between: U and e prod rw
data: VAR object Canada_var
Chi-squared = 28.556, df = 3, p-value = 2.775e-06
Uには他の時系列に対するグレンジャー因果性が存在している可能性があります。
ここで、Instantはグレンジャーの瞬時的因果性というものの検定であり、あまり気にする必要なないようです。
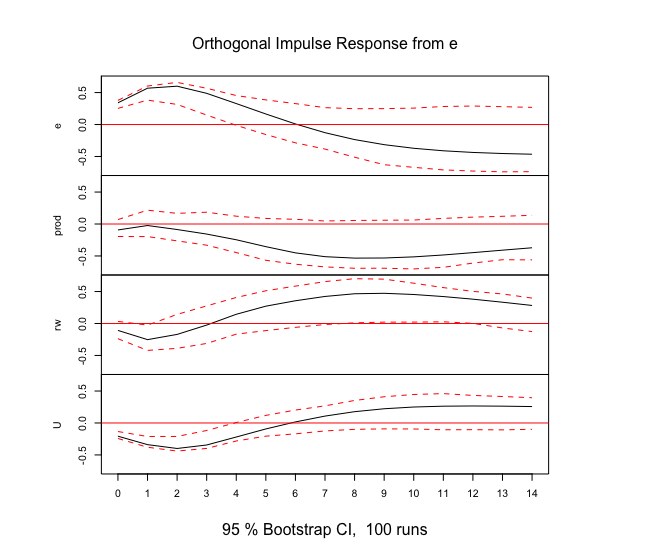
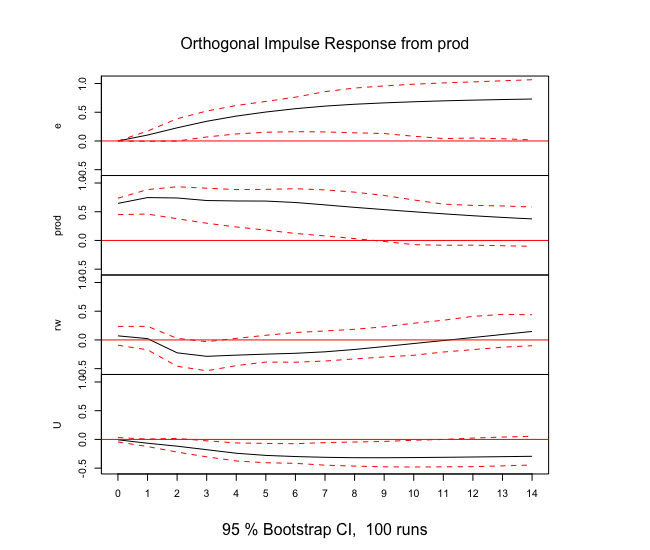
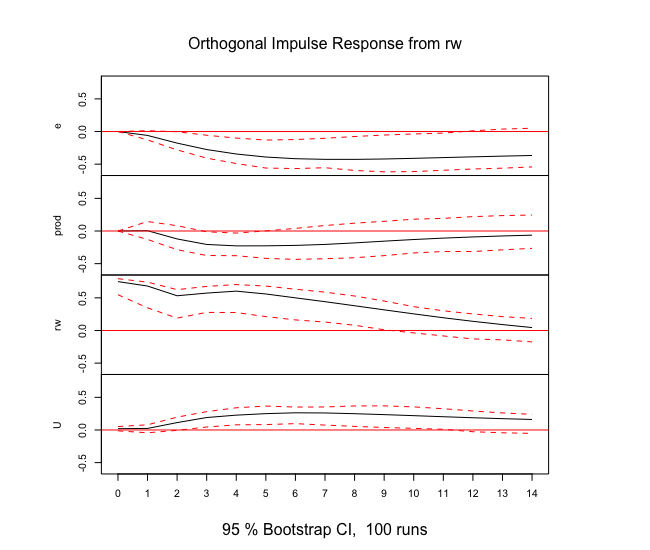
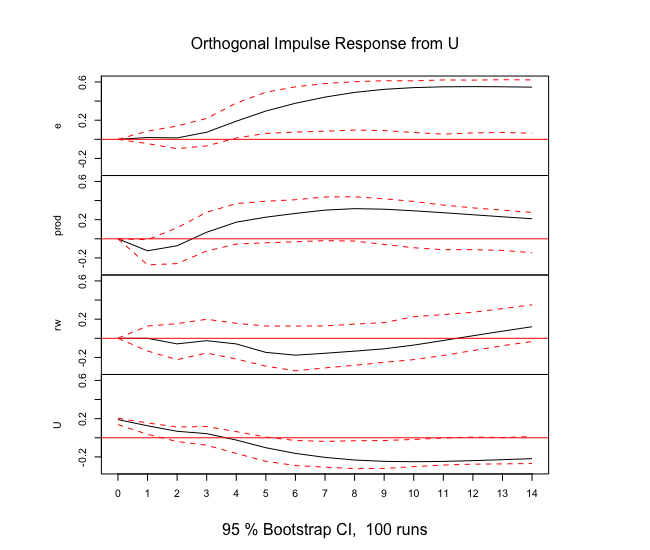
Rでインパルス応答関数の推定
varsパッケージのirf関数を用います。
内部的には直交化インパルス応答により推定しているようです。
# インパルス応答関数
canada_irf<-irf(Canada_var,n.ahead=14,ci=0.95)
結果を可視化してみます。
信頼区間はブートストラップ法で算出されているようです。
plot(canada_irf)
構造VARモデル
VARモデルにおける方程式の全変数は過去のもののみであり、総じて同時点の変数は含みません。
これは、同時点の変数が互いに影響を及ぼすことがないことが仮定されています。
これは非常に強い仮定であり、そう時点の変数が互いに影響を及ぼすことは十分に考えられます。
同時点における変数間の関係を明示的に考慮したモデルを、構造VARモデルと呼びます。
n変数構造VAR(p)モデルは、一般に次のように表すことができます。
B_0 y_t=c+B_1 y_{t-1}+B_2 y_{t-2}+ \dots +B_p y_{t-p}+u_t, u_t \sim W.N.(D)
ここで$B_0$は体格成分が1に等しいn×n行列、$c$はn×1ベクトル、$B_1,\dots,B_p$はn×n行列、$D$はn×n対角行列である。
また、$u_t$は構造錯乱項と呼ばれている。
構造VARモデルは同時方程式モデルであるため、各方程式において説明変数と誤差項が相関を保つため、各方程式をOLSで推定すると同時方程式バイアスが生じてしまうことがあります。
そこで、誘導型と呼ばれる形に変形してから、係数の推定を行います。
誘導型への変形は両辺に$B_0^-1$をかけることで行うことができます。
y_1=B_0^-1c+B_0^-1B_1y_{t-1}+B_0^-1B_2y_{t-2}+\dots+B_0^-1B_py_{t-p}+B_0^{-1}u_t\\
=\Phi_0+\Phi_1y_{t-1}+\Phi_2y_{t-2}+\dots+\Phi_p+\epsilon_t
ここで、$\Phi_0=B_0^-1c,\Phi_i=B_0^-1B_i,\epsilon_t=B_0^{-1}u_t$である。
また、$\epsilon_t$がホワイトノイズであることは、構造撹乱項と同じであるが、$Var(\epsilon)=B_0^{-1}D(B_0^{-1})'$であり、各成分は一般的な相関をもつことに注意しなければならない。
この変換から通常のVARモデルと同じようにOLSによる推定ができます。
そして、OLSによる推定を行なった後に誘導型から構造型に変換する必要があります。
このとき、識別性という問題があり、推定するパラメータ量がVARモデルに比べて多くなるため正しく変換できるとは限らないです。
このような場合に、VARモデルよりも多いパラメータ数分だけ制約を貸さないといけない。よく用いいられる方法は、変数に再帰的構造を課す方法であり、再帰的構造を貸した構造VARモデルは再帰的構造VARモデルと呼ばれています。
Sparse VARモデル
VARモデルの推定にスパース性を加えたものが、Sparse VARモデルです。
が、長くなるので、次に持ち越します。
参考
- https://tjo.hatenablog.com/entry/2013/07/25/194546
- https://tjo.hatenablog.com/entry/2013/07/30/191853
- http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.144.113&rep=rep1&type=pdf
- http://user.keio.ac.jp/~nagakura/R/ts_R2.pdf
(めも)色々調べてて気になったやつ