概要
単眼動画から深度推定モデルを構築する手法を提案した論文「Depth from Videos in the Wild」について解説してみます。これは、ここ1ヶ月続けてきた単眼深度推定モデルに関するシリーズの最終回です。過去の記事は以下の3つです。
本論文で提案されている手法は、struct2depthをベースにしつつも、内部パラメータが未知のときでもうまく訓練できるようにしたという点が新しいところです。これは、丁寧にキャリブレーションされたカメラによって撮影された動画以外でも深度推定モデルが訓練できることを意味し、YouTubeなどに公開されている「in the Wild」な動画も訓練データとして使えるということがポイントです。
本手法の新規性は大きくいって以下の4点となります。
- 内部パラメータの推定
- カメラと物体の並進推定の統合
- オクルージョンを考慮したマスキング処理
- ランダム化されたLayer Normalization
それぞれについて説明した後、ネットワーク構造と損失関数についても軽く触れます。
書誌情報
- Gordon, Ariel, et al. "Depth from videos in the wild: Unsupervised monocular depth learning from unknown cameras." Proceedings of the IEEE International Conference on Computer Vision. 2019.
- https://arxiv.org/pdf/1904.04998.pdf
- 公式実装(Tensorflow)
内部パラメータの推定
カメラの内部パラメータは、単眼深度推定モデルの訓練でよく使用されるKittiデータセットでは既知のものです。しかし、本手法はこの内部パラメータそのものが未知であっても問題ないという汎用的な手法になっています。
問題設定の再確認
基本的な問題設定はSfMLearnerから変わっておらず、動画中での近接するフレーム間で生じる視点の変化と深度推定結果から、適切な別視点合成画像を作れるようにモデルは訓練されます。
数式的には以下のように表現されます。
$z^{\prime} p^{\prime}=K R K^{-1} z p+K t$
$K$はカメラの内部パラメータ、$R, t$はカメラの回転と並進という姿勢変化を表します。そして、ターゲット画像のピクセル$p$とその深度$z$、ソース画像のピクセル$p^{\prime}$と深度$z^{\prime}$が登場人物です。
この式に対応するSfMLearnerの論文中の数式(2)を見てみると、以下のような形になっています。
$p_{s} \sim K \hat{T}_{t \rightarrow s} \hat{D}_{t}\left(p_{t}\right) K^{-1} p_{t}$
深度の表現がやや異なっていますが、大意は同じです。しかし、カメラの姿勢変化は$\hat{T}_{t \rightarrow s}$と表現され、$R, t$がまとまった形で示されていた、ということに注意をしておきましょう。
なぜ内部パラメータを推定可能か
$\hat{T}_{t \rightarrow s}$を$R$と$t$に分離して表現するという何気ない見方の変化が、内部パラメータ$K$が未知のときでも、その値を推定しながら訓練できるという本論文の重要な主張を導いてくれます。
もう一度数式をよく見てみましょう。
$z^{\prime} p^{\prime}=K R K^{-1} z p+K t$
まず、$Kt$について見てみると、$\tilde{K}\tilde{t}=Kt$となる$\tilde{K}(\neq K),\tilde{t}(\neq t)$がいくらでも存在する、ということがわかります。どちらも間違って推定したとしても、同じ結果が得られてしまうので、損失がうまく伝わりません。一方、$K R K^{-1}$はどうでしょうか。証明は本論文のAppendixに譲りますが、こちらに関しては$\tilde{K} \tilde{R} \tilde{K}^{-1}=K R K^{-1}$を満たす$\tilde{K}(\neq K), \tilde{R}(\neq R)$の組み合わせが存在しないということが示されています。そのため、損失がうまく伝わり、$K$は訓練可能で、$R$にも損失が伝わります。そして、間接的に$t$にも損失がうまく伝わります。
なお$R=I$、つまりカメラが一切回転せずに並進しかしていない場合は、$z^{\prime} p^{\prime}=z p+K t$となってしまい、$K$を訓練する手がかりは失われてしまいます。また、$R$が$I$に近いときも、訓練のためのシグナルが相当弱まる、ということが予想できます。
Appendixでは、適切な訓練によって$p, p'$の誤差が1ピクセル未満にできるという仮定を置くと、$K$内の焦点距離$f_x, f_y$の推定誤差$\delta f_{x}, \delta f_{y}$は、$R$内の回転パラメータ$r_x, r_y$を利用して以下の範囲内に収まることを証明しています。
$\delta f_{x}<\frac{2 f_{x}^{2}}{w^{2} r_{y}} ; \quad \delta f_{y}<\frac{2 f_{y}^{2}}{h^{2} r_{x}}$
カメラの回転$r_x, r_y$が十分大きいときに、焦点距離$f_x, f_y$の推定誤差が小さくなる、というわけです。
カメラと物体の並進推定の統合
既存の単眼ビデオからの深度推定モデルの訓練において問題になるのが、周囲の物体の動きです。
本手法では、動きうる物体領域はどこか、そしてそれはどのように動いているのかを推定することで、この問題を回避します。
本手法ではstruct2depthのようなインスタンスセグメンテーションによる前処理と各領域に対するモーション推定という大々的な方法は採用しません。代わりに、より単純化して「動きうる物体領域の推定」と「その領域の並進(回転は無い)の推定」を行います。
動きうる物体の領域の推定と物体の動きの推定として、例えば以下の画像の様な出力が得られます。まず、動きうる物体の領域(possibly mobile mask)は、上段のやや網掛けになっている領域です。また、その領域の並進は、下段のように$x,y,z$がRGBに変換されて表現されています。
ここで気になるのは、画面全体が金色になっていることです。実はこれは、カメラの並進に伴って、画面中の領域全体が近づいて来ている、という並進を表しています。つまり、カメラの並進と物体の並進は、1つの並進マップに統合されて表現されます。
問題設定で示した$z^{\prime} p^{\prime}=K R K^{-1} z p+K t$という式中の$t$は、この並進マップそのもので、ピクセルごとに異なる値になるわけです。
オクルージョンを考慮したマスキング処理
オクルージョンが生じているときに無理に損失を適用するのは良くないことは明らかです。struct2depthでは、monodepth2で提案されていた複数のソース画像から寄ってたかって合成するという方法を採ることで、その影響を軽減しようとしていました。本手法では、もう少し丁寧にこの問題に対処します。
オクルージョンの仕組み
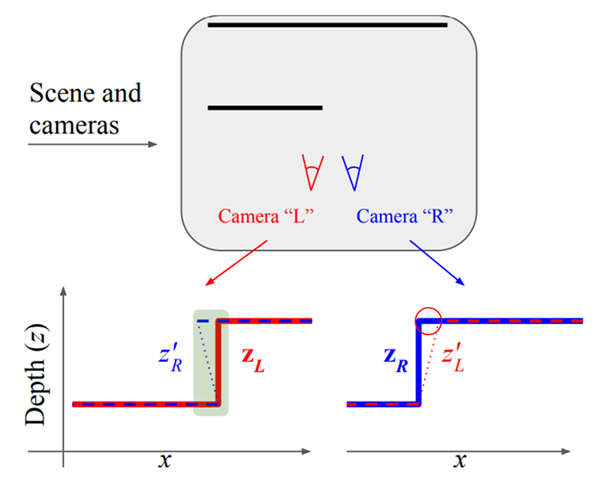
単純化のために、以下のような2枚の平面を撮影するカメラLとRが存在するとします。Lからは見えないけれど、Rの方では見えている奥の平面の領域が存在します。これがオクルージョンです。
深度推定モデルが正しく働いているとすると、Lから撮影した画像に対する深度推定結果は、上図下段左の赤線$Z_L$のようになります。一方、Rで撮影された画像に対する深度推定結果は上図下段右の青線$Z_R$のようになります。また、Lの深度推定をもとにしたRから見たときの合成深度は右の赤点線$Z'_R$、逆は左の青点線$Z'_L$です。
Lから見たときは見えない領域がある、というのは、深度$Z_L$と合成深度$Z'_R$とを比較したときに$Z'_R < Z_L$の領域がある、ということに対応します。また、この領域は$Z_R$と$Z'_L$を比較したときに$Z_R$だけに存在する領域(上図下段右の赤い円)に対応します。
オクルージョン領域の特定手順
ターゲット画像と合成画像の比較を行う際に知りたいのは、ターゲット画像中のある領域がソース画像側からは見えない場所になっているかいないか、ということです。以下のような手順で、そのようなオクルージョン領域の判定を行います。
- ターゲット画像中の座標$(i, j)$について、対応するソース画像の座標($i', j'$)を求める。
- $i', j'$は整数ではないので、ソース深度$Z_s(i', j')$を補間によって求める。
- ターゲット深度をもとに合成された深度$Z'_t(i', j')$を求める。
- 合成深度$Z'_t(i', j')$とソース深度$Z_s(i', j')$を比較し、$Z'_t(i', j') < Z_s(i', j')$ならオクルージョンが発生しているため、ターゲット画像の座標$(i, j)$については損失を計算しない。
オクルージョンを考慮した事による効果
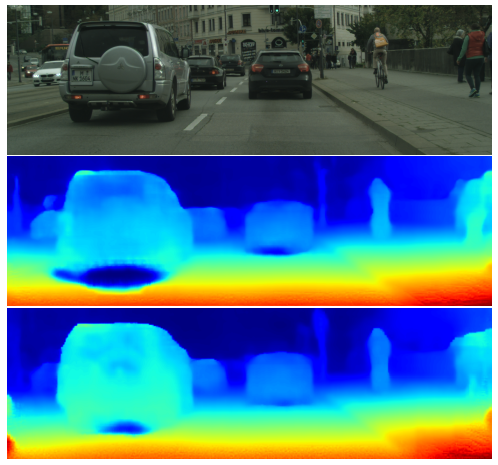
以下はオクルージョンを考慮した訓練を行った場合にどのような改善が得られるのかを示した画像です。
車の下は常に隠されている場所なので、オクルージョンが生じやすい場所です。そこでは推定深度が崩れやすい(下図だと、青くなっているので無限遠)わけですが、中段のオクルージョンを考慮しないケースに対し、下段のオクルージョンを考慮したケースでは推定深度の崩れが小さくなっています。
ランダム化されたLayer Normalization
深度を推定するネットワークでは、もともとBatch Normalizationを使っていたそうですが、なぜかtraining modeにしないとtest推論時精度が悪くなってしまう、ということがわかったそうです。また、訓練時にバッチサイズを増やすと、目に見えて精度が悪化したそうです。
Batch Normalizationのtraining modeとtest modeとの違いは、正規化に用いる平均と分散とがオンラインで更新されているかそうでないかという違いです。というわけで、training modeにしないと推論精度が劣化してしまう、というのは平均と分散をオンラインで調整するか、入力されたサンプルのみに従って正規化したほうが良い、のではないかという仮説が立てられます。
そこで、例えばLayer Normalizationを使えば良いのではという発想になりますが、実際に置き換えてみたところ、深度推定の精度は劣化してしまったそうです。
では何が原因なのか? 著者らは、Batch Normalizationでは平均と分散の計算過程に、ミニバッチ内の多様なサンプルが含まれており、それが「良いノイズと」して機能しているのではないか、という仮説を立てます。このようにして考えると、訓練中のバッチサイズを増やすことによって生じる精度劣化は、平均と分散とが安定しすぎるためなのではないか、という説明がつきます。
以上の考察から、Layer Normalizationで計算される平均と分散に、明示的にノイズを入れるこを提案しています。この工夫は、推論時の明らかな精度向上だけでなく、訓練時にバッチサイズを増やしても問題ないという結果をもたらしています。
ネットワーク構造
一通り新規性について確認してきたので、ネットワーク構造を確認し、新規性がどのように盛り込まれているのかを確認しましょう。
深度推定
Depthを1枚の画像から推定するネットワークは、ベースがResNet-18のU-Netアーキテクチャとなっています。
最終出力は、SoftPlus($z = \log(1 + e^l)$)によってlogitからdepthに変換します。
ランダム化されたLayerNormalizationがここで導入されています。
カメラ姿勢と並進、内部パラメータの推定
カメラの姿勢と並進、及び内部パラメータの推定は、同一のネットワークで行います。
FlowNetをベースにしたネットワークになっており、オプティカルフローを算出するようなモデルになっています。
このネットワークはグローバルなオプティカルフローといえるカメラ姿勢の変化$r_0, t_0$を推定し、同時に、焦点距離とオフセット、および歪係数も推定されます。
FlowNetのEncoder出力をもとに、Decoder側では徐々に解像度を上げながら、ピクセルレベルでのオプティカルフロー$\delta{t}(x, y)$が算出されます。各解像度での出力結果は、次の解像度では2倍され、次の解像度の出力と足し合わされるというresidualな構造が採用されています。
possibly mobile maskは事前学習済みセグメンテーションモデルから推定され、$m(x, y)$と表現されます。これと組み合わせて、全体的な並進マップは、以下のようにして得られます。
$t(x, y)=t_{0}+m(x, y) \delta t(x, y)$
この並進マップ$t$は、$z^{\prime} p^{\prime}=K R K^{-1} z p+K t$で使われます。
損失関数
損失関数では、オクルージョンを考慮した損失計算領域のマスキングが全面的に採用されています。
Occlusion aware L1 Penalty
L1損失として、以下の2つが挙げられています。これらは、オクルージョンを考慮して、その領域は除外して算出されます。
- RGB:ソース画像を元に作成した合成画像とターゲット画像のRGB値を直接比較します。
- Depth:深度にも損失がかかります。ソース深度をもとに合成した合成深度マップとターゲット深度マップを比較します。
Cycle Consistency
ソース画像の座標をターゲット画像の座標に移したあと、またソース画像の座標に戻したときに、できるだけ同じ位置に戻っているべきというサイクル損失を考えます。こちらも、オクルージョンを考慮して、その領域は損失から除外します。
重み付きSSIM
合成画像とターゲット画像のRGBにおける損失として、SSIMも採用しています。
SSIMは、近接するピクセルが存在することを前提としているので、オクルージョンを考慮すると適用しにくいです。
そこで、合成深度とターゲット深度の不一致が大きい場所では小さくなるような重みを考えます。深度の不一致のRMSを算出し、それよりも不一致が大きい場所は重みを0にします。
まとめ
以上、Depth from Videos in the Wildで提案された手法について紹介しました。
内部パラメータのキャリブレーションなしに深度推定モデルが訓練できるという本手法は、単眼深度推定手法の現時点でのひとつの到達点と言えるのではないでしょうか。
以下の図の一番左に示すような極端な歪みがかかった動画でも、適切な深度推定ができています。また、オクルージョンを考慮した訓練は、結果的に前景物体領域と背景領域の境界を明確にしていることもわかります。