はじめに
とある事情から,ベジェ曲線の分割について調べていたのですが,
$n$次ベジェ曲線の分割方法について解説しているサイトがあまり見当たりませんでした.
まぁ,ベジェ曲線なんて高々4次ぐらいまでしか使わないので$n$次なんて分からなくても問題ないのですが,
どうしても綺麗に実装したくて調べたので知識として残しておこうと思います.
一応記事内にも実装例を載せましたが,GitHubにも上げています( line_module.py 参照).
再帰を利用した手法
De Casteljau のアルゴリズム(De Casteljau's algorithm)と呼ばれる手法です.
この方法では再帰を利用して,分割後の新しいベジェ曲線の制御点を求めます.
この手法は考え方が単純で実装も容易ですが,スタックサイズが小さい組み込み系などでは使いにくいという欠点があります.まぁ,ベジェ曲線なんて高々4次ぐらいまでしか(略
アルゴリズム
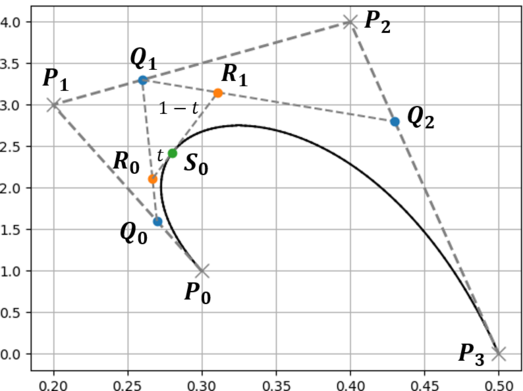
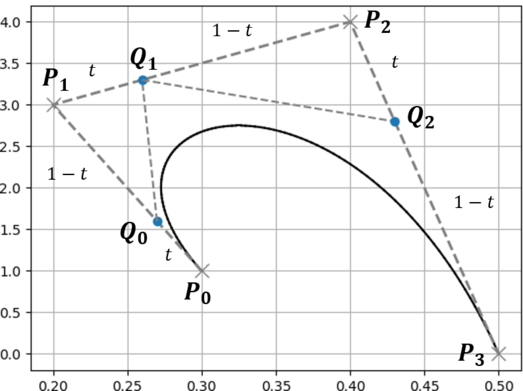
例として下に示すベジェ曲線を分割するものとします.
分割地点におけるベジェ曲線の媒介変数を $t$ とし,ベジェ曲線の初期の制御点を $P_i$ とします.
1. ベジェ曲線の制御点を結んだ線において $t:1-t$ となる点を求める(点$Q$).
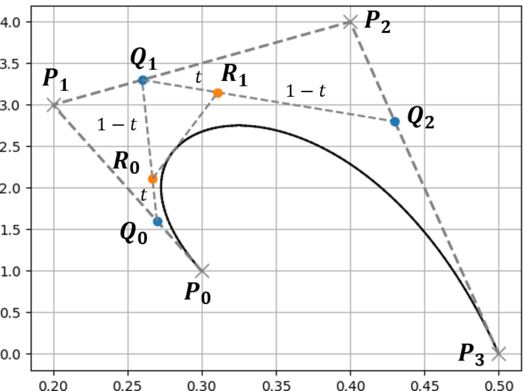
2. 求めた点を結んだ線に対して,同様に $t:1-t$ となる点を求める(点$R$).
4. 初期の制御点を含めた全ての点で,添字が最小の点の集合と最大の点の集合が分割後の制御点となる.
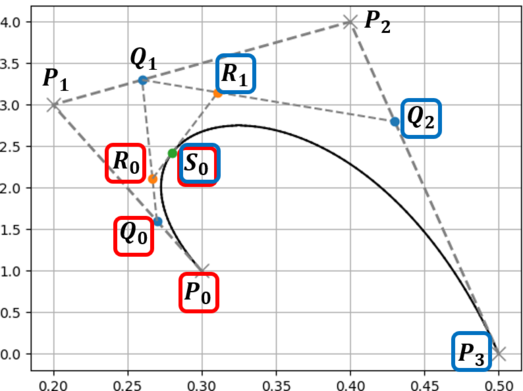
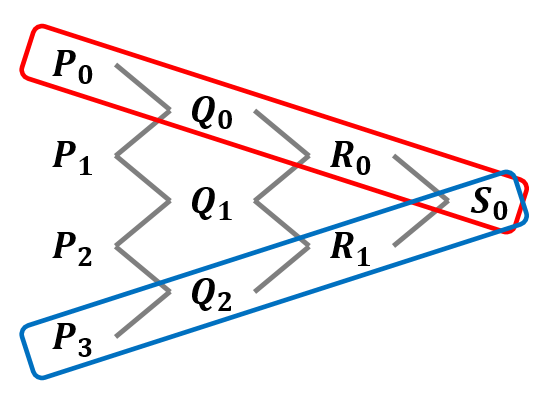
最後の部分(添字が最小の~)については,下のような木構造を書いてみると理解しやすいと思います.
下に示す木構造は,どの線分(どの2点)から新しい点が生成されたかを表したものになっています.
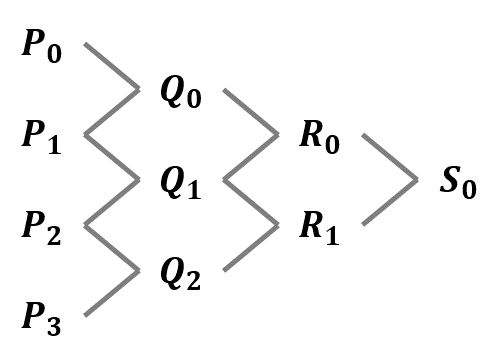
この木構造のうち一番外側の点,すなわち点 $\{ P_0, Q_0, R_0, S_0 \}$ と点 $\{ S_0, R_1, Q_2, P_3 \}$ が新しいベジェ曲線となります.元のベジェ曲線の始点と終点が共通であることや,媒介変数 $t$ における点(分割地点 $S_0$)が新しいベジェ曲線の始点(終点)になっていることがわかると思います.
プログラム
再帰を利用した分割プログラムの実装例を以下に示します.
import numpy as np
from scipy.special import comb
import matplotlib.pyplot as plt
class Bezier:
def __init__(self, points):
points = [np.array(e).flatten() for e in points]
self._n = len(points)
self._points = points
@property
def dims(self):
return self._n - 1
@property
def points(self):
return self._points
@property
def points4matplot(self):
xs, ys = zip(*self.points)
return xs, ys
def _bernstein(self, n, i, t):
return comb(n, i) * t**i * (1 - t)**(n-i)
def bezier_point(self, t):
p = np.zeros(2)
for i, f in enumerate(self.points):
p += self._bernstein(self.dims, i, t) * f
return np.array(p).flatten()
def _de_casteljau_algorithm(self, points, t):
prev_p = None
q = []
for p in points:
if not prev_p is None:
## Split line into t:(1-t)
q.append(np.array((1-t) * prev_p + t * p).flatten())
prev_p = p
if len(q) == 1:
return [q]
return [q] + self._de_casteljau_algorithm(q, t)
def split_with_recursion(self, t):
ret = [self.points] + self._de_casteljau_algorithm(self.points, t)
lp = []
rp = []
for lst in ret:
## Fetch min and max point
lp.append(lst[0])
rp.append(lst[-1])
return Bezier(lp), Bezier(rp)
def plot(self, ax=None, with_ctrl_pt=True, bcolor="black", ccolor="gray", resolution=100):
if ax is None:
_, ax = plt.subplots()
prev_point = None
for t in np.linspace(0, 1, resolution):
bp = self.bezier_point(t)
if prev_point is None:
prev_point = (bp[0], bp[1])
xs, ys = zip(*(prev_point, (bp[0], bp[1])))
ax.plot(xs, ys, '-', color=bcolor)
prev_point = (bp[0], bp[1])
if with_ctrl_pt:
xs, ys = self.points4matplot
ax.plot(xs, ys, 'x--', lw=2, color=ccolor, ms=10)
return ax
def main():
bezier = Bezier([(0.3, 1), (0.2, 3), (0.4, 4), (0.5, 0)])
ax = bezier.plot()
left_bezier, right_bezier = bezier.split_with_recursion(0.3)
left_bezier.plot(ax, bcolor = "red")
right_bezier.plot(ax, bcolor = "blue")
plt.grid()
plt.show()
if __name__ == "__main__":
main()
行列を利用した手法
行列を使って新しい制御点を求める手法です.
この方法ではスタックサイズが小さくても問題ない反面,計算が少々複雑になります.
まぁ,ベジェ曲線なんて高々4次(略
ベジェ曲線を行列の形で表す
アルゴリズムを説明する前段階として,ベジェ曲線の行列表現について説明します.
ベジェ曲線は次のような式で表すことができます.
\begin{align}
F(t) &= \sum_{i=0}^{n} P_i~B_{i}^{n}(t)
\end{align}
$P_i$ は制御点,$B_{i}^{n}(t)$ はバーンスタイン基底関数を表します.
$n$ はベジェ曲線の次数に$1$を足した数($=$ 制御点の数)を表します.
これを行列の積の形で表すと次のようになります.
\begin{align}
F(t) &= \sum_{i=0}^{n} P_i~B_{i}^{n}(t) \\
&= \left(
\begin{array}{ccc}
B_{0}^{n} & B_{1}^{n} & \dots & B_{n}^{n}
\end{array}
\right)
\left(
\begin{array}{ccc}
P_0 \\
P_1 \\
\vdots \\
P_n
\end{array}
\right)
\end{align}
また,ベジェ曲線の式を $t$ について整理すると次のように表すことができます.
ここでの $a_n$ は適当な係数を表しています.
\begin{align}
F(t) &= \sum_{i=0}^{n} P_i~B_{i}^{n}(t) \\
&= \left(
\begin{array}{ccc}
1 & t & t^2 & \dots & t^n
\end{array}
\right)
\left(
\begin{array}{ccc}
a_0 \\
a_1 \\
\vdots \\
a_n
\end{array}
\right)
\end{align}
以上のことから次のような式を導くことができます.
\begin{align}
F(t) &=
\left(
\begin{array}{ccc}
B_{0}^{n} & B_{1}^{n} & \dots & B_{n}^{n}
\end{array}
\right)
\left(
\begin{array}{ccc}
P_0 \\
P_1 \\
\vdots \\
P_n
\end{array}
\right)
=
\left(
\begin{array}{ccc}
1 & t & t^2 & \dots & t^n
\end{array}
\right)
\left(
\begin{array}{ccc}
a_0 \\
a_1 \\
\vdots \\
a_n
\end{array}
\right) \\ \\
F(t) &= BP = XA
\end{align}
だいぶ綺麗になりました.
ここで,$A$ はある下三角行列 $U_t$ と 制御点 $P$ によって次のように表せることが分かっています.
\begin{align}
A &= U_tP \\ \\
&= \left(
\begin{array}{ccc}
{n \choose 0} {n \choose 0} (-1)^0 & 0 & \cdots & 0 \\
{n \choose 0} {n \choose 1} (-1)^1 & {n \choose 1} {n-1 \choose 0} (-1)^0 & \cdots & 0 \\
\vdots & \vdots & \cdots & \vdots \\
{n \choose 0} {n \choose n} (-1)^n & {n \choose 1} {n-1 \choose n-1} (-1)^{n-1} & \cdots & {n \choose n} {n-n \choose n-n} (-1)^{n-n} \\
\end{array}
\right)
\left(
\begin{array}{ccc}
P_0 \\
P_1 \\
\vdots \\
P_n
\end{array}
\right)
\end{align}
したがって,最終的にベジェ曲線の式は,行列を用いて次のように表すことができます.
F(t) = BP = XU_tP
アルゴリズム
行列を使ったベジェ曲線分割のアルゴリズムは次のようになります.
1. ベジェ曲線を $t$ について整理して行列の形で表す.
\begin{align}
F(t) &= XU_tP \\
&= \left(
\begin{array}{ccc}
1 & t & t^2 & \dots & t^n
\end{array}
\right)U_tP \\
\end{align}
2. 分割地点 $z ~(z \in t)$ を分離する.
\begin{align}
F(t) &= \left(
\begin{array}{ccc}
1 & t & t^2 & \dots & t^n
\end{array}
\right)U_tP \\ \\
&= \left(
\begin{array}{ccc}
1 & (z\cdot t) & (z\cdot t)^2 & \dots & (z\cdot t)^n
\end{array}
\right)U_tP \\ \\
&= \left(
\begin{array}{ccc}
1 & t & t^2 & \dots & t^n
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & & & & 0 \\
& z & & & \\
& & z^2 & & \\
& & & \ddots & \\
0 & & & & z^n
\end{array}
\right)U_tP
\end{align}
3. 次のように式変形を行い,$Q$ を求める.
\begin{align}
F(t) &= \left(
\begin{array}{ccc}
1 & t & t^2 & \dots & t^n
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & & & & 0 \\
& z & & & \\
& & z^2 & & \\
& & & \ddots & \\
0 & & & & z^n
\end{array}
\right)U_tP \\
&= X ~ Z U_t ~ P \\ \\
&= X ~ U_t U_t^{-1} Z U_t ~ P \\ \\
&= X ~ U_t Q ~P
\end{align}
上の計算では $U_t$ の位置を移動させています.
$U_t U_t^{-1}$ は単位行列になるので計算結果自体は変化しません.
$Q = U_t^{-1}ZU_t$ となります.
4. $QP$ を計算し新しいベジェ曲線の制御点を算出する.
\begin{align}
F(t) &= X ~ U_t Q ~P \\
&= X ~ U_t ~ P^{~\prime}
\end{align}
$P^{~\prime} = QP$ とするとベジェ曲線を表す式の形になります.
したがって$P^{~\prime}$ が分割後のベジェ曲線の制御点となります.
以上の手順によって分割した左側のベジェ曲線を求めることができました.
右側のベジェ曲線を求めるときは手順2において $z$ を次のようにしてから分離させ,
右側用の行列 $Q^{~\prime}$ を求めます.
\begin{align}
F(t) &= \left(
\begin{array}{ccc}
1 & t & t^2 & \dots & t^n
\end{array}
\right)U_tP \\ \\
&= \left(
\begin{array}{ccc}
1 & (z + (1-z)\cdot t) & (z + (1-z)\cdot t)^2 & \dots & (z + (1-z)\cdot t)^n
\end{array}
\right)U_tP
\end{align}
しかし,実際には直接計算せずとも計算済みの $Q$ を用いて $Q^{~\prime}$ を求めることができます.
具体的には,
- $Q$ の要素を $0$ の分右側に詰める.
- 右に詰めた行列の要素を上下反転する.
という操作をするだけです.
数式を用いた説明が難しいので,次の計算例の節を参照してください.
計算例
「$n$次の話ばっかりじゃよく分からん!」という人のために,行列計算による分割の計算例を載せておきます.
今回は例として,
$P_0=(0, 1),~ P_1=(1, 4),~ P_2=(2, 0)$
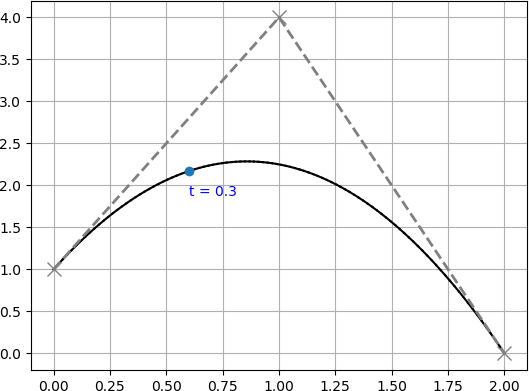
を制御点に持つ2次ベジェ曲線を $t=0.3$ の位置で分割するとします.
図で表すと下図のような曲線です.
まず,このベジェ曲線を行列の形で表し,分割地点 $z=0.3$ を分離します.
\begin{align}
F(t) &= XZU_tP \\
&=
\left(
\begin{array}{ccc}
1 & t & t^2
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & z & 0 \\
0 & 0 & z^2
\end{array}
\right)
\left(
\begin{array}{ccc}
{2 \choose 0}{2 \choose 0}(-1)^0 & 0 & 0 \\
{2 \choose 0}{2 \choose 1}(-1)^1 & {2 \choose 1}{1 \choose 0}(-1)^0 & 0 \\
{2 \choose 0}{2 \choose 2}(-1)^2 & {2 \choose 1}{1 \choose 1}(-1)^1 & {2 \choose 2}{0 \choose 0}(-1)^0
\end{array}
\right)
\left(
\begin{array}{ccc}
P_0 \\
P_1 \\
P_2
\end{array}
\right) \\ \\
&=
\left(
\begin{array}{ccc}
1 & t & t^2
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0.3 & 0 \\
0 & 0 & 0.09
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
-2 & 2 & 0 \\
1 & -2 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
P_0 \\
P_1 \\
P_2
\end{array}
\right)
\end{align}
ここで $Q=U_t^{-1}ZU_t$ を計算します.
\begin{align}
Q &= U_t^{-1}ZU_t \\ \\
&=
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
1 & \frac{1}{2} & 0 \\
1 & 1 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0.3 & 0 \\
0 & 0 & 0.09
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
-2 & 2 & 0 \\
1 & -2 & 1
\end{array}
\right) \\ \\
&=
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0.7 & 0.3 & 0 \\
0.49 & 0.42 & 0.09
\end{array}
\right)
\end{align}
式変形を行い,$Q$ を利用した式にします.
\begin{align}
F(t) &= XZU_tP \\
&= XU_tU_t^{-1}ZU_tP \\
&= XU_tQP \\
&=
\left(
\begin{array}{ccc}
1 & t & t^2
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
-2 & 2 & 0 \\
1 & -2 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0.7 & 0.3 & 0 \\
0.49 & 0.42 & 0.09
\end{array}
\right)
\left(
\begin{array}{ccc}
P_0 \\
P_1 \\
P_2
\end{array}
\right)
\end{align}
ここで $QP$ について計算すると,
\begin{align}
QP &=
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0.7 & 0.3 & 0 \\
0.49 & 0.42 & 0.09
\end{array}
\right)
\left(
\begin{array}{ccc}
P_0 \\
P_1 \\
P_2
\end{array}
\right) \\ \\
&=
\left(
\begin{array}{ccc}
P_0 \\
0.7P_0 + 0.3P_1 \\
0.49P_0 + 0.42P_1 + 0.09P_2
\end{array}
\right) \\ \\
&= P^{~\prime} \\ \\
\end{align}
\begin{align}
P^{~\prime}_x &=
\left(
\begin{array}{ccc}
0 \\
0.7\cdot 0 + 0.3 \cdot 1 \\
0.49\cdot 0 + 0.42\cdot 1 + 0.09\cdot 2
\end{array}
\right)
=
\left(
\begin{array}{ccc}
0 \\
0.3 \\
0.6
\end{array}
\right)
\end{align}
\begin{align}
P^{~\prime}_y &=
\left(
\begin{array}{ccc}
1 \\
0.7\cdot 1 + 0.3 \cdot 4 \\
0.49\cdot 1 + 0.42\cdot 4 + 0.09\cdot 0
\end{array}
\right)
=
\left(
\begin{array}{ccc}
1 \\
1.9 \\
2.17
\end{array}
\right) \\
\end{align}
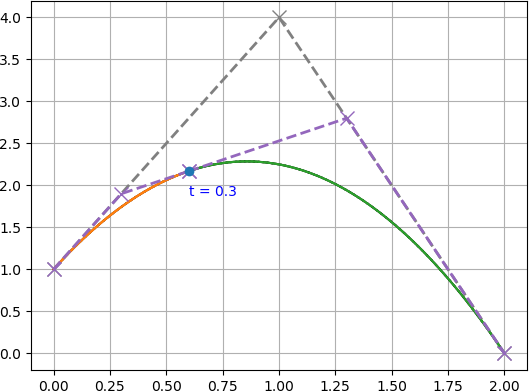
となり,**分割した左側のベジェ曲線の制御点**が $P_0^{~\prime}=(0, 1),~ P_1^{~\prime}=(0.3, 1.9),~ P_2^{~\prime}=(0.6, 2.17)$ であることが分かりました.
次は右側のベジェ曲線を求めていきます.
右側用の $U_t^{-1}Z^{~\prime}U_t = Q^{~\prime}$ は計算した $Q$ を利用して次のように求めることができます.
1. $Q$ の要素を $0$ の分右側に詰める.
\begin{align}
Q &=
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0.7 & 0.3 & 0 \\
0.49 & 0.42 & 0.09
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{ccc}
0 & 0 & 1 \\
0 & 0.7 & 0.3 \\
0.49 & 0.42 & 0.09
\end{array}
\right)
\end{align}
2. 右に詰めた行列の要素を上下反転する.
\begin{align}
\left(
\begin{array}{ccc}
0 & 0 & 1 \\
0 & 0.7 & 0.3 \\
0.49 & 0.42 & 0.09
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{ccc}
0.49 & 0.42 & 0.09 \\
0 & 0.7 & 0.3 \\
0 & 0 & 1
\end{array}
\right)
= Q^{~\prime}
\end{align}
簡単ですね.
求めた $Q^{~\prime}$ を使うと分割した右側のベジェ曲線を求めることができます.
\begin{align}
Q^{~\prime}P &=
\left(
\begin{array}{ccc}
0.49 & 0.42 & 0.09 \\
0 & 0.7 & 0.3 \\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
P_0 \\
P_1 \\
P_2
\end{array}
\right) \\ \\
&=
\left(
\begin{array}{ccc}
0.49P_0 + 0.42P_1 + 0.09P_2 \\
0.7P_1 + 0.3P_2 \\
P_2
\end{array}
\right) \\ \\
&= P^{~\prime\prime} \\ \\
\end{align}
\begin{align}
P^{~\prime\prime}_x &=
\left(
\begin{array}{ccc}
0.49\cdot 0 + 0.42\cdot 1 + 0.09\cdot 2 \\
0.7\cdot 1 + 0.3 \cdot 2 \\
2
\end{array}
\right)
=
\left(
\begin{array}{ccc}
0.6 \\
1.3 \\
2
\end{array}
\right)
\end{align}
\begin{align}
P^{~\prime\prime}_y &=
\left(
\begin{array}{ccc}
0.49\cdot 1 + 0.42\cdot 4 + 0.09\cdot 0 \\
0.7\cdot 4 + 0.3 \cdot 0 \\
0
\end{array}
\right)
=
\left(
\begin{array}{ccc}
2.17 \\
2.8 \\
0
\end{array}
\right)
\end{align}
これで右側のベジェ曲線の制御点が $P_0^{~\prime\prime}=(0.6, 2.17),~ P_1^{~\prime\prime}=(1.3, 2.8),~ P_2^{~\prime\prime}=(2, 0)$ であることが分かりました.
$P_0 = P_0^{~\prime}$,$P_2^{~\prime} = P_0^{~\prime\prime}$,$P_2 = P_2^{~\prime\prime}$ であることから,うまく分割できていそうですね.
求めた左側のベジェ曲線と右側のベジェ曲線を描画すると下図の様になります.
うまいこと分割できていますね.
プログラム
行列を利用した分割プログラムの実装例を以下に示します.
import numpy as np
from scipy.special import comb
import matplotlib.pyplot as plt
class Bezier:
def __init__(self, points):
points = [np.array(e).flatten() for e in points]
self._n = len(points)
self._points = points
@property
def dims(self):
return self._n - 1
@property
def points(self):
return self._points
@property
def points4matplot(self):
xs, ys = zip(*self.points)
return xs, ys
def _bernstein(self, n, i, t):
return comb(n, i) * t**i * (1 - t)**(n-i)
def bezier_point(self, t):
p = np.zeros(2)
for i, f in enumerate(self.points):
p += self._bernstein(self.dims, i, t) * f
return np.array(p).flatten()
def split_with_matrix(self, t):
M = self.create_Ut()
iM = np.linalg.inv(M)
Z = np.eye(self.dims + 1)
for i in range(self.dims + 1):
Z[i] = Z[i] * t ** i
## Caluclate Q
Q = iM @ Z @ M
xs, ys = self.points4matplot
X = np.array(xs)
Y = np.array(ys)
left_bezier = Bezier(list(zip(Q @ X, Q @ Y)))
## Make Q'
_Q = np.zeros((self.dims + 1, self.dims + 1))
lst = []
for i in reversed(range(self.dims + 1)):
l = [-1] * i + list(range(self.dims + 1 - i))
lst.append(l)
for i, l in enumerate(lst):
mtx = [Q[i][e] if not e == -1 else 0 for e in l]
_Q[i] = np.array(mtx)
_Q = np.flipud(_Q)
right_bezier = Bezier(list(zip(_Q @ X, _Q @ Y)))
return left_bezier, right_bezier
def create_Ut(self, dims=None):
if dims is None:
dims = self.dims
U = np.zeros([dims + 1, dims + 1])
lmbd = lambda n, i, j: comb(n, j) * comb(n-j, i-j) * (-1)**(i - j)
for i in range(dims + 1):
lst = list(range(i+1)) + [-1]*(dims-i)
elems = [lmbd(dims, i, j) if j >= 0 else 0.0 for j in lst]
mtx = np.array(elems)
U[i] = mtx
return U
def plot(self, ax=None, with_ctrl_pt=True, bcolor="black", ccolor="gray", resolution=100):
if ax is None:
_, ax = plt.subplots()
prev_point = None
for t in np.linspace(0, 1, resolution):
bp = self.bezier_point(t)
if prev_point is None:
prev_point = (bp[0], bp[1])
xs, ys = zip(*(prev_point, (bp[0], bp[1])))
ax.plot(xs, ys, '-', color=bcolor)
prev_point = (bp[0], bp[1])
if with_ctrl_pt:
xs, ys = self.points4matplot
ax.plot(xs, ys, 'x--', lw=2, color=ccolor, ms=10)
return ax
def main():
bezier = Bezier([(0, 1), (1, 4), (2, 0)])
ax = bezier.plot()
left_bezier, right_bezier = bezier.split_with_matrix(0.3)
left_bezier.plot(ax, bcolor = "red")
right_bezier.plot(ax, bcolor = "blue")
plt.grid()
plt.show()
if __name__ == "__main__":
main()
おわりに
本記事では$n$次ベジェ曲線の分割について紹介しました.
あまりまとまっていなかったかもしれませんが,ご容赦ください.
本記事の内容が誰かのお役に立てれば幸いです.