はじめに
後輩の研究でベジェ曲線と直線の交点を求める必要がありました.
研究のお手伝いをしていた私は,
「Pythonなら強々ライブラリとか簡潔な実装例とかあるでしょ!余裕余裕 ![]() 」
」
とか思っていたのですが,私にも理解できるレベルで書いてある記事が見つけられませんでした.
仕方なく,比較的簡単そう&多少の解説PDFが見つけられたBezierClipping法という手法に焦点を定め,
論文を読み漁って理解・実装したので,その知識を残しておこうと思います.
記事中に多少正確性に欠ける表現があるかもしれませんがご了承ください(そして訂正例を教えて下さい).
実装したコードはGitHubに公開しています.
ベジェ曲線ってなんぞ?
ベジェ曲線(Bezier Curve)は曲線の表し方の一種です.
アウトラインフォントやCG等コンピュータ上で曲線を表すときによく利用されています.
ベジェ曲線は曲線の始点と終点に加えて,制御点(Control Point)と呼ばれるいくつかの点で構成されます.
以降では始点と終点も含めて制御点と呼称します.
ベジェ曲線は媒介変数 $t$ $(0\leq t \leq 1)$を用いて次のように表されます.
\begin{align}
P(t) &= \sum_{i=0}^{n} F_i B_{i}^{n}(t) \\
&= \sum_{i=0}^{n} F_i {n \choose i} t^i \left(1-t \right)^{n-i}
\end{align}
$F_i$ は制御点,$B_{i}^{n}$ はバーンスタイン基底関数(Bernstein Basis Polynomials)です.
また,${n \choose i}$ は組み合わせ(combination)を表します.
世界標準はこの書き方らしいですが,日本の高校で習ったように書くと下のようになります.
P(t) = \sum_{i=0}^{n} F_i ~~ {}_n \mathrm{C} {}_r ~~ t^i \left(1-t \right)^{n-i}
ベジェ曲線は $t$ $(0\leq t \leq 1)$における点の集合なので,
$t$ の刻み幅を細かくすればするほど曲線がなめらかになります.
以下に刻み幅を変えた場合の例を出します.灰色の$\times$点は制御点を表しています.
$(0\leq t \leq 1)$を5分割した場合 (5点だけ計算した場合).

$(0\leq t \leq 1)$を10分割した場合 (10点だけ計算した場合).

$(0\leq t \leq 1)$を50分割した場合 (50点だけ計算した場合).

$(0\leq t \leq 1)$を100分割した場合 (100点だけ計算した場合).

BezierClipping 法
概要
BezierClipping 法はベジェ曲線の性質を利用して曲線と直線の交点を求める手法です.
西田らによって1990年に提案されました.
特徴としては以下のような点が挙げられています(一部抜粋).
- 指定した範囲の全ての解(交点)が求出可能
- 安定して解を求められる
- 解の有無の判定が高速
- 解を小さい順に算出可能
- 1次式のみの反復計算 ...etc
ベジェ曲線同士の交点や3次元空間における交点などにも応用できるようですが,
今回はベジェ曲線と直線に限定します.
アルゴリズム
アルゴリズムの大まかな流れは次の通りです.
1. 対象のベジェ曲線を直線との距離を表すベジェ曲線に変換する($xy$ 平面から $td$ 平面へ変換する).

2. 変換したベジェ曲線の制御点の凸包(convex-hull)を求め,$t$ 軸との交点 $t_{min}, t_{max}$ を求める.

3. 求めた $t_{min}, t_{max}$ でベジェ曲線を分割し,新しいベジェ曲線とする.

4. 2-3の処理を区間 $[t_{min},~ t_{max}]$ が十分小さくなるまで繰り返す.

5. 求まった $t$ (上図の赤点) が直線との交点における元のベジェ曲線の媒介変数 $t$ となる.
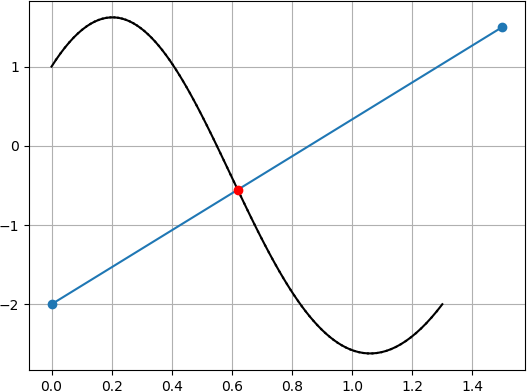
アルゴリズム自体は非常に単純ですね.
おそらく詰まるところは
- ベジェ曲線の変換処理
- 複数交点が存在するときの処理
だと思うので,次節で詳しく説明します.
ベジェ曲線の変換処理
二次元平面座標空間を前提とします.
平面空間内にある直線 $L$ は次のように表すことができます.$a, b, c$ は定数です.
ax + by + c = 0
座標空間内の任意の点 $(x_1, y_1)$ と直線 $L$ の距離 $d$ は次のように表せます.
d = \frac{ax_1+by_1+c}{\sqrt{a^2 + b^2}}
ここで,ベジェ曲線上の点 $(x, y)$ は $t$ を媒介変数として次のように求められます.
$(x_i, y_i)$はベジェ曲線の制御点を表します.
\begin{align}
x(t) &= \sum_{i=0}^{n} x_i B_i^n (t) \\
y(t) &= \sum_{i=0}^{n} y_i B_i^n (t)
\end{align}
これらを使い,直線 $L$ とベジェ曲線間の距離 $D$ は次のように表せます.
\begin{align}
D &= \frac{ax(t)+by(t)+c}{\sqrt{a^2+b^2}} \\ \\
&= \frac{1}{\sqrt{a^2+b^2}}\left( a\sum_{i=0}^{n} x_i B_i^n (t) + b\sum_{i=0}^{n} y_i B_i^n (t) + c \right)
\end{align}
$\sum_{i=0}^{n} B_i^n (t) = 1$ であるので,
\begin{align}
D &= \frac{1}{\sqrt{a^2+b^2}}\left( a\sum_{i=0}^{n} x_i B_i^n (t) + b\sum_{i=0}^{n} y_i B_i^n (t) + c\sum_{i=0}^{n} B_i^n (t) \right) \\ \\
&= \frac{1}{\sqrt{a^2+b^2}}\sum_{i=0}^{n} (ax_i+by_i+c) B_i^n (t) \\ \\
&= \frac{1}{\sqrt{a^2+b^2}}\sum_{i=0}^{n} d_i B_i^n (t)
\end{align}
ここで $D$ は制御点 $\left(\frac{i}{n}, d_i \right)$ から成る有理ベジェ曲線となります.
また $D$ は $td$ 平面のベジェ曲線,すなわち横軸 $t$ 縦軸 $d$をとる平面空間におけるベジェ曲線になります.
変換したベジェ曲線 $D$ が,ある $t ~(0 \leq t \leq 1) $ において $d=0$ をとるということは,
その $t$ 値において変換前の $xy$ 平面におけるベジェ曲線と直線間の距離がゼロになることを意味しています.
したがって,直線とベジェ曲線の交点における媒介変数 $t$ が算出できたことになります.
あとは下式に交点における媒介変数 $t$ を入れれば,$xy$ 平面における交点の座標が求まります.
\begin{align}
x(t) &= \sum_{i=0}^{n} x_i B_i^n (t) \\
y(t) &= \sum_{i=0}^{n} y_i B_i^n (t)
\end{align}
複数点が存在するときの処理
複数の交点が存在するときの処理は簡単です.
複数の交点が存在する場合は $t_{min}$ と $t_{max}$ の変化が小さくなります.
例を下図に示します.図中の青点が1つ前の $t_{min}, t_{max}$ の点を表しています.
3回目から $t_{min}, t_{max}$ の位置がほぼ変わっていないことが分かります.
この場合は曲線を適当な点で分割し,それぞれのベジェ曲線に対して再度 BezierClipping 法を適用します.
分割する点に関しては言及されていないようでした.
私の実装では中点で分割するようにしています.
おわりに
本記事ではBezierClipping 法について解説しました.
私は最初の変換の部分がなかなか理解できずにかなり苦労しました.
本記事の内容が誰かのお役に立てれば幸いです.



