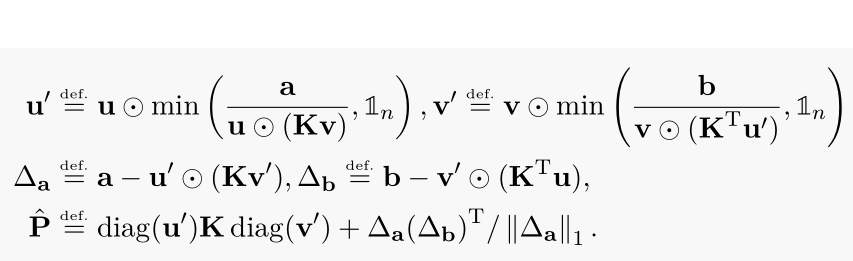Computational Optimal Transport 精読会 記録 (#11: 4.2 その1)

背景

• 前回: Computational Optimal Transport 精読会 記録 (#10: 4.1)は5/28に遠隔で参加した．JSAIを挟んでしばらくあいて6/11に開催した．
• 職場でCOTを読んでおり，{自己満足,復習,将来のため}などの理由で記録をしている

今回の範囲の内容

• 著名なSinkhornアルゴリズムについて学んでいく
• §4.2はとても長いので少しずつ読んでいく

§4.2 Sinkhorn's Algorithm and Its Convergence

• §4.1で定義したエントロピー正則化付きの輸送問題を思い出す
• Coupling matrix $\bf P$のmarginalsが$\bf a, b$になるという制約があるので，これは$nm$変数の自由度と見せかけて$n+m$程度

$$L^\varepsilon_C({\bf a}, {\bf b}) = \min_{{\bf P}\in U({\bf a},{\bf b})} \langle {\bf P}, C\rangle - \varepsilon H({\bf P})$$

• 実はこの最適化問題の解$\bf P$は常に特別な形になる，というのがProp. 4.3

Prop. 4.3

• ある2つのベクトル $\mathbf{u} \in \mathbb{R}_+^n$ と $\mathbf{v}\in\mathbb{R}_+^m$ を用いて以下の形になる:

$$\mathbf{P}_{i,j} = \mathbf{u}_i K_{i,j} \mathbf{v}_j$$

Prop. 4.3の証明

• $\mathbf{P} 1_m = a, \mathbf{P}^T 1_n = b$ という2つの$U$に関する制約を思い出す．
• それぞれ $n$ 個， $m$ 個の制約式なので，それぞれにラグランジュの未定乗数 $f_i$ と $g_j$ を用意し，制約なし最適化問題を考える
• 目的関数 $\mathcal{E}(\mathbf{P,f,g})$ の偏微分から

$$\frac{\partial\mathcal{E}}{\partial\mathbf{P}_{i,j}} = C_{i,j} + \varepsilon \log \mathbf{P}_{i,j} - \mathbf{f}_i - \mathbf{g}_j$$

• これを$\mathbf{P}_{i,j}$について解くと $\mathbf{P}_{i,j}=\exp(\mathbf{f}_i/\varepsilon) \exp(-C_{i,j}/\varepsilon) \exp(\mathbf{g}_j/\varepsilon)$ となる
• 例えば $u_i = \exp(\mathbf{f}_i/\varepsilon)$ とすると，Prop 4.3を得る

行列表現

• 上のProp 4.3を行列表現すると $\mathbf{P} = \mathrm{diag}(\mathbf{u}) K \mathrm{diag}(\mathbf{v})$ となる
• $U(\mathbf{a,b})$の条件を満たすことから，
  • $\mathrm{diag}(\mathbf{u}) K \mathrm{diag}(\mathbf{v}) 1_m = \mathbf{a}$
  • $\mathrm{diag}(\mathbf{v}) K^T \mathrm{diag}(\mathbf{u}) 1_n = \mathbf{b}$
    • これは転置記号を分配して$u, v$がひっくり返る
• $\mathrm{diag}(\cdot)$を書き直すと
  • $\mathbf{u} \odot (K\mathbf{v}) = \mathbf{a}$
  • $\mathbf{v} \odot (K^T\mathbf{u}) = \mathbf{b}$

漸化式 = Sinkhorn's Algorithm

• 上の関係性が恒等式として成り立つ（＝coupling matrixの制約を満たす）と考えると，以下の漸化式を得る

$$\mathbf{u}^{(l+1)} = \frac{\mathbf{a}}{\mathbf{Kv}^{(l)}}$$

$$\mathbf{v}^{(l+1)} = \frac{\mathbf{b}}{\mathbf{K}^T\mathbf{u}^{(l + 1)}}$$

• 適当な初期値 $\mathbf{v}^{(0)}$ から計算をはじめていく
• 適当なスケーリング（スカラ$\lambda$と$1/\lambda$を両ベクトルに掛ける）においても同値の目的関数値が得られるので，初期値依存性がある
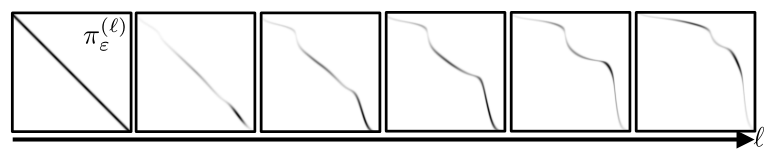
• 初期値として恒等写像からはじめた場合の計算の進行具合が図4.5に載っている

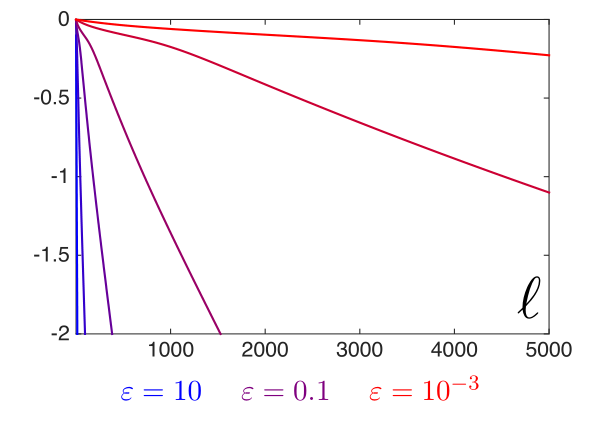
• エントロピー正則化のパラメータ $\varepsilon$ の影響についても載っている．収束速度に影響を与える．

• アルゴリズムの収束性の理論解析は様々にされている

Remark 4.6

• Altschuler et al. 2017の議論を紹介（詳細には入らない）（本は間違っているかも？）
• Altschuler et al.の修正式が紹介されている

• どういう意味があるか（推測）
  • Sinkhornアルゴリズムは，単純に計算しただけではfeasibleでない解 (正しくない$\mathbf{P}$) になっている可能性がある
  • これを修正する操作になっている
  • これを踏まえて解析するとき，誤差が抑えられるという議論がRemark 4.6

Remark 4.7

• 数値的安定性の話
• 特に$\varepsilon$が小さくなると，発散したりゼロ除算が発生したりする
  • これはlogドメインで実装すれば軽減される

Remark 4.8

• Sinkhornアルゴリズムは，$P\in U(a, b)$に対して，行和と列和が$a, b$になることを両方同時に満たすようなアルゴリズムを考えている

• これを分けて考え，行和だけを考える集合$\mathcal{C}_a$と，列和だけを考える集合$\mathcal{C}_b$を導入する

  • つまり $U(a, b) = \mathcal{C}_a \cap \mathcal{C}_b$

• 前回議論したKLダイバージェンスを利用したProjを，それぞれ$\mathcal{C}_a$と$\mathcal{C}_b$で計算するとどうなるか，という話（更新ステップの設計がSinkhornと異なる）

• 詳細はアフィン集合に対するBregmanダイバージェンスのProjを調べよう

• 結論はSinkhornが良い

Next

• 6/18に開催