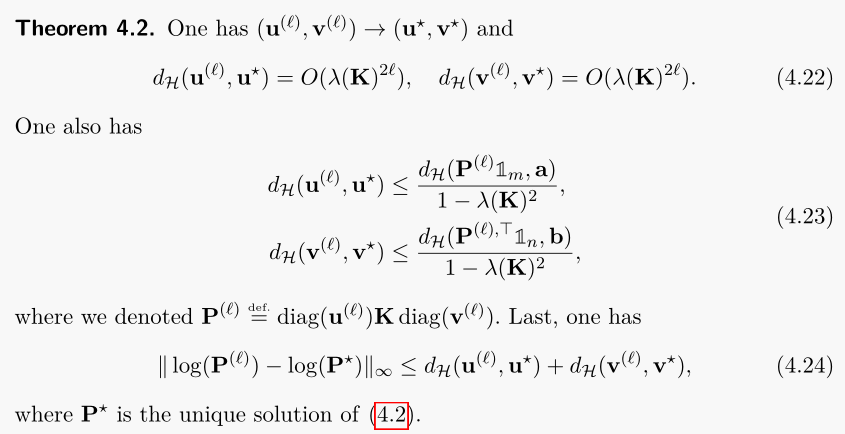背景
- 前回: Computational Optimal Transport 精読会 記録 (#12: 4.2 その2)は6/18に開催,今回は6/28に開催
- 職場でCOTを読んでおり,{自己満足,復習,将来のため}などの理由で記録をしている
前回の振り返りと今回の内容
- エントロピー正則化付きの輸送問題
- $L^\varepsilon_C({\bf a}, {\bf b}) = \min_{{\bf P}\in U({\bf a},{\bf b})} \langle {\bf P}, C\rangle - \varepsilon H({\bf P})$
- Sinkhornアルゴリズム最高
- $\mathbf{u}^{(l+1)} = \frac{\mathbf{a}}{\mathbf{Kv}^{(l)}}$, $\mathbf{v}^{(l+1)} = \frac{\mathbf{b}}{\mathbf{K}^T\mathbf{u}^{(l + 1)}}$
- Hilbert projective metricは縮小写像である(Theorem 4.1)
- 今回: Sinkhornアルゴリズムの収束性について,Hilbert projective metricの縮小写像を用いて議論する
- 前回からの続き
Remark 4.13 ペロンフロベニウスの定理
-
少し気分転換して(嘘),線形代数やページランクの話で出てくるPerron-Frobeniusの話に寄り道する
- CS的にはマルコフ連鎖が定常分布に収束する,という話をするときに出てくる
- マルコフ連鎖はあるベクトルに遷移確率行列 (二重確率行列) を掛けていくと収束するという話
- Sinkhornと似ている (重要)
-
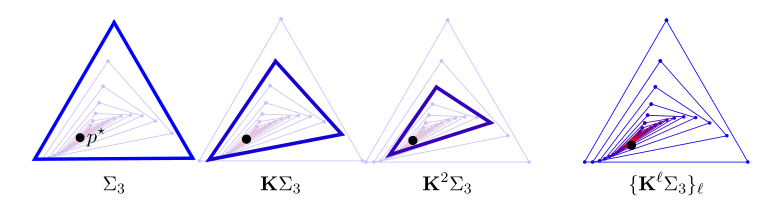
固有ベクトルを考えると,$\mathbf{K}p^* = p^*$
-
そのため,適当な初期値$p_0$に$l$回$K$を適用した結果どうなるか,を議論できる
- $d(\mathbf{K}^lp_0, p^\star) = d(\mathbf{K}^lp_0, \mathbf{K}^lp^\star) \leq \lambda(K)^l d(p_0, p_\star)$
- 不等式はTheorem 4.1より
-
縮小写像の動作イメージがのっている
Remark 4.14 Sinkhornアルゴリズムの収束性
- 主張: $l$回Sinkhornアルゴリズムを適用したとき,(4.22),(4.23),(4.24)が成り立つ.それぞれ次のような式.
Remark 4.14の証明
-
$d(v, v')$の定義から,これは次のように変化しても同じ
- $v, v'$は$m$次元ベクトルとする (太字になってないのは面倒だから)
- $d(v, v') = d(v/v', 1_m) = d(1_m/v, 1_m/v')$
-
Sinkhornアルゴリズムの更新式(上の方に書いてある)から,$d(u^{(l+1)}, u^\star) = d(Kv^{(l)}, Kv^\star) \leq \lambda(K) d(v^{(l)}, v^\star)$
- これは$v\to u$の話なので,もう一回Sinkhornアルゴリズムの分を展開すると,$u\to v\to u$と更新するときに$\lambda(K)$は$2l$のオーダで寄与する.よって(4.22)を得る.
-
式(4.23)は三角不等式から得ることが出来る
-
式(4.24)は難しいので詳細は論文参照になっている
Remark 4.15 SinkhornアルゴリズムのLocal divergenceについて
- 式が間違っているらしい (4.25)
- 難しくて分からなかった
Next
- §4.3へ進もう