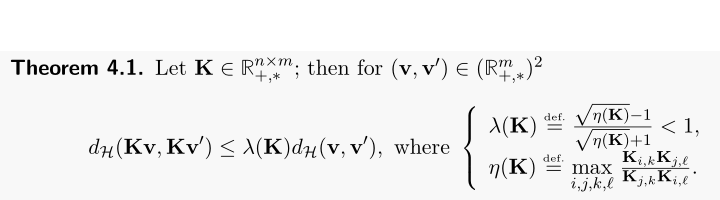Computational Optimal Transport 精読会 記録 (#12: 4.2 その2)

背景

• 前回: Computational Optimal Transport 精読会 記録 (#11: 4.2 その1)は6/11に開催，今回は6/18に開催
• 職場でCOTを読んでおり，{自己満足,復習,将来のため}などの理由で記録をしている

前回の振り返り

• エントロピー正則化付きの輸送問題

  • $L^\varepsilon_C({\bf a}, {\bf b}) = \min_{{\bf P}\in U({\bf a},{\bf b})} \langle {\bf P}, C\rangle - \varepsilon H({\bf P})$

• Sinkhornアルゴリズム最高

  • $\mathbf{u}^{(l+1)} = \frac{\mathbf{a}}{\mathbf{Kv}^{(l)}}$, $\mathbf{v}^{(l+1)} = \frac{\mathbf{b}}{\mathbf{K}^T\mathbf{u}^{(l + 1)}}$

今回の範囲の内容

• 著名なSinkhornアルゴリズムとその関連話題について§4.2を読み進めていく（続き）

Remark 4.9

• Sinkhornアルゴリズムとは別として，エントロピー正則化付きの最適化問題についてもう少し考えていく
• 正則化がついていない解 (ε = 0) に対して，εを徐々に小さくしながらSinkhornアルゴリズムを解いていけば，そのうち$P$ が求まる
• これを KL-div. に対する proximal point algorithm として捉える
• 制約なし目的関数を置く
  • ここで$\iota_C(x)$は$x\in C$のときに0を，それ以外は∞を返す指示関数

$$F(P) := \langle P, C\rangle + \iota_{U(a, b)}(P)$$

• ある $P^{(l)}$ を更新する proximal operator として以下を定義する

$$\mathrm{Prox}_{\frac{1}{\varepsilon}F}^\mathbf{KL}(\mathbf{P}^{(l)}) := \arg\min_{P\in\mathbb{R}_+^{n\times m}} \mathbf{KL}(\mathbf{P}\mid \mathbf{P}^{(l)}) + \frac{1}{\varepsilon} F(\mathbf{P})$$

• これを用いて $\mathbf{P}^{(l+1)} = \mathrm{Prox}_{\frac{1}{\varepsilon}F}^\mathbf{KL}(\mathbf{P}^{(l)})$ とする
• これは詳細な議論は省略するとして，エントロピー正則化付きの輸送問題を解くSinkhornアルゴリズムと似た問題を解いている
• そのため初期値として $\mathbf{P}^{(0)} = 1_n 1_m^T$とし，更新していくことで，次のような解の形になる

$$\mathbf{P}^{(l+1)} = \mathrm{diag}(\mathbf{u}^{(l)}\odot\dots\odot\mathbf{u}^{(0)}) \exp(\frac{-(l+1)C}{\varepsilon}) \mathrm{diag}(\mathbf{v}^{(0)}\odot\dots\odot\mathbf{v}^{(l)})$$

• またこのような問題は，正則化パラメータ$\varepsilon$の代わりに，$\varepsilon/l$という形にしたSinkhornアルゴリズムによって解くことが出来る（嬉しい）

Remark 4.10

• 輸送問題ではエントロピー正則化をやっていた
• 実はその他の正則化項を付与している場合でもいける
• アルゴリズム的にもよく研究されている（Bregman）
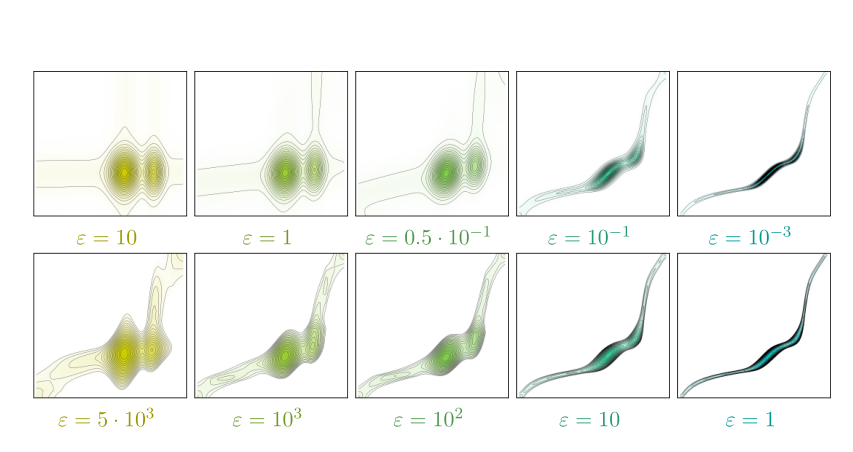
• 輸送問題に限った場合，次のような違いが見て取れる
  • (コメント) 上段中央の$10^{-1}$は間違い
  • 上段がエントロピー，下段が二乗ノルムの制約式と指示関数

Remark 4.11

• Barycentric projectionの話，ムズイ

Remark 4.12

• Sinkhornアルゴリズムの大域的な収束解析についての議論
• 初期には Hilbert projective metric という空間について議論されていた
  • これは $d(u, u') = \log\max_{i,j}\frac{u_i, u'_j}{u_j, u'_i}$ というmetric に関する議論がされた
  • これはスケーリングについて無視されるような商空間での距離となっている
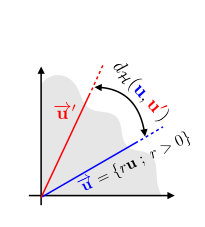
• 図が多少はわかりやすいか
  • 定数倍を無視するので，線と線の間で距離を計測するような空間（角度という意味ではない）

• 距離空間であることの証明

  • $d(u, u) = 0$ は，$\max_{i,j}$ を具体的に要素として書き出すと，当然，比がある$r$になっているので，ここから得る
  • $d(u, v) = d(v, u)$ は自明
  • 三角不等式は，$\max$を外して割り算のところに要素を補って$\log$をバラすことで示せる

• このあたりの一つ一つの性質は示すのが難しかったのであまりやってない（やっている人もいた）

• 以降の議論ではTheorem 4.1が必要

Theorem 4.1

• ベクトル$v,v'$が行列$K$で変換されているとき，これが元の間の距離と$1$より小さい定数倍のスケーリングで抑えられる = 縮小写像になっているという定理
  • 証明は本にも載っていない

Next

• 次回，これを利用して，Sinkhornアルゴリズム（ベクトルに行列とかを書けたりしていくアルゴリズム）がどういう挙動を示しているのかについて議論していく