CUDDの簡単な利用例: ランダムな論理関数の作成

環境をインストールしてGraphviz経由の作図ができるようになったので、ランダムな論理関数を作ってみる。

考えた方法

• 変数の数（BDDの高さ） $N$は固定
• $2^N$ 通りの組み合わせを考える（= 0から1<<Nまで）
• 個別の組み合わせ $i$ について、乱数を使って0/1を決定
• 1の場合、組み合わせ $i$ を論理式 $f_i$ で表現
• 全ての1の場合を足し合わせる

実装

• 前回の記事: CUDDの簡単な利用例: Graphvizを用いた可視化でテストしたADD経由の可視化で確認してみる。

#include <iostream>
#include <random>
#include <vector>
#include "cuddObj.hh"

using namespace std;

int main() {
  Cudd mgr;

  // 乱数生成機
  std::random_device rd;
  std::mt19937 mt(rd());
  std::uniform_int_distribution<int> bin(0, 1);

  // 桁数4 (= 変数の個数)
  const int N = 4;
  vector<BDD> X(N);
  for (int i = 0; i < N; i++)
    X[i] = mgr.bddVar(); // 変数Xiの作成

  BDD f = mgr.bddZero();
  for (int i = 0; i < (1 << N); i++) {
    int bj = bin(mt);
    if (bj == 1) {
      BDD termi = mgr.bddOne();
      for (int k = 0; k < N; k++)
        termi &= (i & (1 << k)) ? X[k] : !X[k];
      f |= termi; // fiを足し合わせる
    }
  }

  // dot dump
  const vector<ADD> vec = {f.Add()};
  auto fp = fopen("dot/random.dot", "w");
  const char* iname[4] = {"x1", "x2", "x3", "x4"};
  const char* oname[1] = {"F"};
  mgr.DumpDot(vec, iname, oname, fp);
  return 0;
}

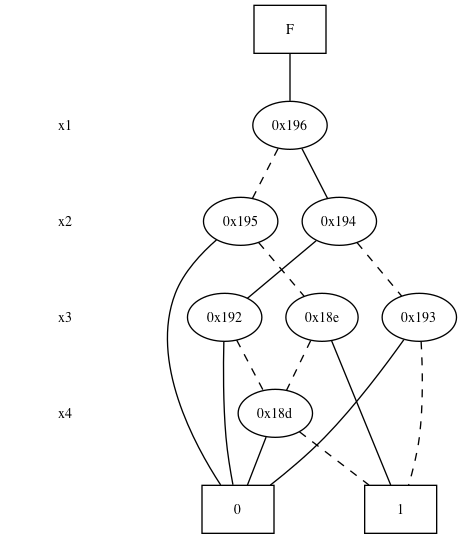
• 出力結果
  • 図から逆算すると、$x_1 \bar{x_2} \bar{x_3} \vee \bar{x_1} \bar{x_2} x_3 \vee \bar{x_1} \bar{x_2} \bar{x_3} \bar{x_4} $ なのかな