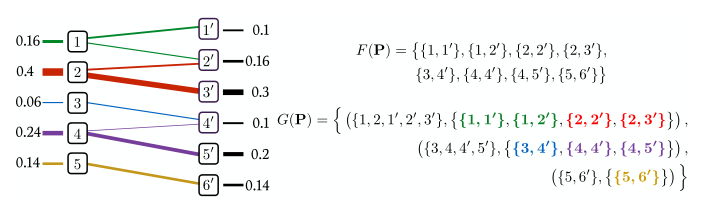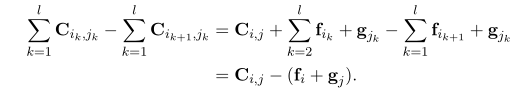背景
- 前回: Computational Optimal Transport 精読会 記録 (#6: 3.3-3.4)は4/16に開催,今回は4/23に開催
- 職場でCOTを読んでおり,{自己満足,復習,将来のため}などの理由で記録をしている
今回の範囲の内容
- §3.3-3.4でやっていた外点と主問題・双対問題の性質および二部グラフにおける議論を続けていく
アンチョコ
-
Kantorovich problem: $L_C(\mathbf{a,b}) = \min_{\mathrm{P}\in U(\mathbf{a, b})} \langle C, P \rangle$, $U(a, b) = \{\mathrm{P}\in \mathbb{R}_+^{n\times m}\mid \mathrm{P} \mathbb{1}_m = \mathbf{a}, \mathbf{P}^T \mathbb{1}_n = \mathbf{b} \}$
-
Dual problem $L_C(\mathbf{a,b}) = \max_{(\mathbf{f, g})\in R(C)} \langle \mathbf{f, a}\rangle + \langle \mathbf{g, b}\rangle$, $R(C) = \{(\mathbf{f,g})\in\mathbb{R}^n\times \mathbb{R}^m \mid \mathbf{f \oplus g} \leq C\}$
-
$G({\bf P})$は輸送が存在する山の間に辺をはった二部グラフ
-
complementary: もし${\bf P}_{i,j} > 0$ (輸送する)ならば,$C_{i,j} = {\bf f}_i + {\bf g}_j$であること
-
feasible: $\mathbf{f} \oplus \mathbf{g} \leq \mathbf{C}$であること (負の要素を持たないこと)
§3.5 A Heuristic Description of the Network Simplex
-
ネットワークシンプレックス法の概念を説明していく
-
前提その1: Prop3.3で,あるcoupling matrix $P$はfeasibleかつcomplementaryであれば最適である
-
前提その2: NW corner ruleによって$U(a,b)$の外点${\bf P}$を作成できる
-
ネットワークシンプレックス法の考え方
- あるfeasibleな解${\bf P}$から,complementaryな${\bf f, g}$を構築できる
- もし${\bf f, g}$がfeasibleであれば,最適解である
- もし${\bf f, g}$がinfeasibleであるとき,$P$を修正することで現在の解を更新していき,最終的に最適な解に到達する
§3.5.1 Obtaining a dual pair complementary to P
- 項目1.に対応する,つまり${\bf f}_i + {\bf g}_j = C_{i,j}$であるように設定する
- まず$G({\bf P})$を思い出すと,対応関係が$s=|S({\bf P)|$として,一般に辺の数よりも変数の数が多いため,非決定になっている
- そこでグラフ構造を利用し,端から順番に数値を確定していく
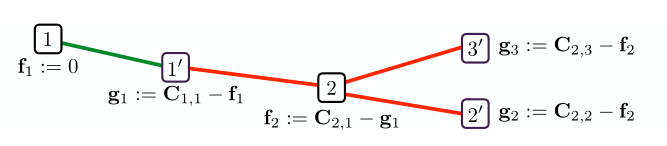
- 例題はFigure 3.3: 3つの木から構成される森になっている
- 各木(つまり連結成分)ごとに,ある端っこのポテンシャルを決定し,complementary条件を伝搬させて値を決定する
- いまいち不親切な例だと思ったが,どうも3.3と3.4は関係があって一応成り立っているらしい(教えてもらった)
- これによってポテンシャルを決定できるため,ある$\bf P$からcomplementaryな$\bf f, g$が構成できる
§3.5.2 Network Simplex Update
- 次に項目2.と3.に関して議論する
- もし作られた$\bf f, g$がfeasibleであれば,これはProp 3.3より最適解になっているため,何もしなくていい
- そこで項目3.の場合,何らかの方法で更新作業が必要になる
- 今feasibilityが達成されていない$(i,j)$があるとする
- このような$(i,j)$に対応する辺$(i,j')$をグラフ$G$に付与して考えていく
ケース1
- $(i,j')$を追加してもグラフ$G$が森である場合を考える
- このとき新しい辺$(i,j')$を入れたことで,新しいベクトル$\bf f, g$を計算できる
- このとき,グラフは変化するが,主問題の解$P$は何もしておらず,変化しない
- memo:反復アルゴリズムと考えると,英語の代名詞がどの解を指している少し説明が分かりづらく混乱するところがある
ケース2
- $(i,j')$を追加した結果,グラフ$G$がサイクルを持ってしまう
- 先に述べた通り,サイクルを持っている場合はextremalでなくなり,シンプレックス法で頂点を動きながら最適化をしていることにならなくなる(たぶん),そこでこれを解消するためにサイクルを取り除く操作によってグラフを改変する
- サイクルを取り除く操作は,前回使った少し$\epsilon$を足して結果として$P_{i,j}\to 0$として辺を取り除くという手法がある(グラフが変わる)
- 補足: §3.4でサイクルを持たないことを証明した技法と類似
- こうして新しく作成したグラフから拘束条件を伝搬させ,新しい$\bf f,g$が構築できる
(§3.5.2のまとめ)
- 結果として,どちらのケースでも更新が可能
§3.5.3 Improvement of the primal solution
- 上の操作でグラフを変更したとき,対応している主問題の解$P$も変化するが,このときどうなっているか
- §3.5.3で示す通り,解は改善している(より良いか,少なくとも同値な解になっている)
- 証明としては,ある加えられた辺を$(i,j)$と表し,$i_{l+1}=i_1=i$という表記によって証明できる
- TeXを打つのが面倒になったのでコピペしてメモ
§3.5の疑問
- Network simplexは説明が詳細にされているが,イマイチ不明瞭で読んでいても結論が出なかった点を書き残しておく
- アルゴリズムは止まる?(頂点を移動するアナロジーとしては,$U(a,b)$がboundedなので止まるはずだが,グラフで言われると?)
- Vertexとかfeasibleとかの関係性がよく分からない(いじった解$P$がvertexかどうかは保証されているのか?)
次回
- GW後の5/8に予定