背景
- 前回: Computational Optimal Transport 精読会 記録 (#5: 3.1-3.2)は4/10に開催,今回は4/16に開催
- 職場でCOTを読んでおり,{自己満足,復習,将来のため}などの理由で記録をしている
今回の範囲の内容
- 主に2章でやってきた最小化問題(Kantrovich problem)と最大化問題(Dual problem)の性質を議論する (復習含む)
アンチョコ
-
Kantorovich problem: $L_C(\mathbf{a,b}) = \min_{\mathrm{P}\in U(\mathbf{a, b})} \langle C, P \rangle$, $U(a, b) = \{\mathrm{P}\in \mathbb{R}_+^{n\times m}\mid \mathrm{P} \mathbb{1}_m = \mathbf{a}, \mathbf{P}^T \mathbb{1}_n = \mathbf{b} \}$
-
Dual problem $L_C(\mathbf{a,b}) = \max_{(\mathbf{f, g})\in R(C)} \langle \mathbf{f, a}\rangle + \langle \mathbf{g, b}\rangle$, $R(C) = \{(\mathbf{f,g})\in\mathbb{R}^n\times \mathbb{R}^m \mid \mathbf{f \oplus g} \leq C\}$
§3.3 Complementary Slackness
- 主問題と双対問題の間には(弱/強)双対定理によって関連するが,問題としては別々に解くことが可能
- 主問題の最適解を$\mathbf{P}^\star$,双対問題の最適解を$\mathbf{f^\star, g^\star}$でそれぞれ表す
- Prop 3.2は解の関係性を説明する
Prop 3.2
-
arXiv版では式の参照番号がデタラメになっているので注意
- 例: arxiv版の(2.24), (2.11)はそれぞれ(2.11)と(2.20)の間違い
-
主張: 最適解の条件から,任意の山のインデクスペア$(i,j)$について,${\bf P}^\star_{i,j}(C_{i,j} - ({\bf f}^\star_i + {\bf g}^\star_j)) = 0$が成り立つ
- これは輸送量が0になるか,ポテンシャルが共に0になることを意味する
-
証明
- 強双対定理より目的関数値が一致する: $\langle P^\star, C\rangle = \langle f^\star, a\rangle + \langle g^\star, b\rangle$ ということ
- またmarginal $a, b$はcoupling matrixの定義より$P^\star 1_m = a, P^{\star T} 1_n = b$である
- また要素積の和$\langle \cdot, \cdot \rangle$は分解すると要素を左右に入れ替えられるようになる
- 式変形によって主張が成り立つ
-
このProp3.2から以下の名称を新しく定義
- complementary: もし$P_{i,j} > 0$ (輸送する)ならば,$C_{i,j} = f_i + g_j$であること
-
Complenetaryかつfeasibleな輸送について,次の定理が成り立つことが分かる
Prop 3.3
- 主張: Complementaryかつfeasibleな輸送は最適である
- 証明: 弱双対性とcomplementaryの定義から成り立つ
メモ
- 結局タイトルのComplementary Slacknessはどういう意味の単語なのかよく分からなかった
- スラック変数的なことをなにか言っているのか,それとも合わせて1単語なのか
§3.4 Vertices of the transportation polytope
-
式3.4でやることは,主に今までCoupling matrixといっていた輸送$P$がどのようなものなのか?を議論する
-
特に,線形計画の基本的な事実として(ここからあまり正確ではない表現)最適解が凸多面体の頂点にある(ここまで)という事実とどう関連するのかを説明していく
- 補足: extremal point: もし$x = (y + z) / 2$という点が存在するとき,$x=y=z$に限る
-
この節はそこそこ数式の誤りがあるが,全体的に議論展開は問題ない(だいたい)
-
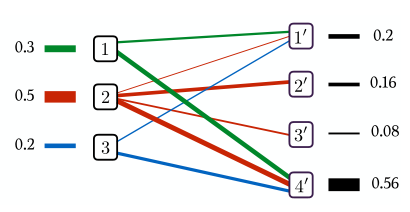
まずヒストグラム間の輸送(左側から右側に運ぶ)というアイデアを,二部グラフで描く(本文Figure 3.1)
- 左の山から右の山に,各経路を通ってどれだけずつ輸送するか,という問題を考えていた.
3.4.1
- 解となる$P$をグラフの言葉で特徴つけたものがProp 3.4になる.
Prop 3.4
-
主張: 二部グラフのうち,$P_{i,j} > 0$である場合のみ辺を貼ったグラフを$G(P)$で表す.もし$P$が$U(a,b)$のextremal pointであるとき,$G(P)$はサイクルを持たない.つまりグラフ$G(P)$の辺は最大$n+m-1$本になる.
-
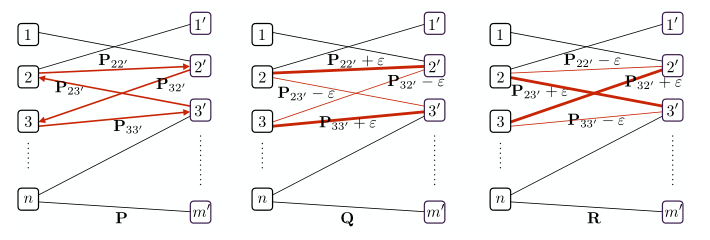
証明: 後半はグラフ理論から成り立つ.前半を示すために,具体的にサイクルを持った解を構成してみると良い(Figure 3.2)
- 左: 外点であるにもかかわらず,サイクルである例があったとする
- 中/右: それぞれ$\epsilon$ずつ輸送量を変化させた2つの輸送を構成する
- $\epsilon$が十分小さいとき,これはcoupling matrixになっているので,$U(a,b)$の要素である
- また$P = (Q + R) / 2$である
- しかしこのとき$P=Q=R$になっていないため,$P$が外点であるという前提が誤っており,主張が成り立つ.
3.4.2
- 外点が解になり,それがサイクルを持たないことが示されたが,具体的にどのように$U(a,b)$の外点を構成すればよいか
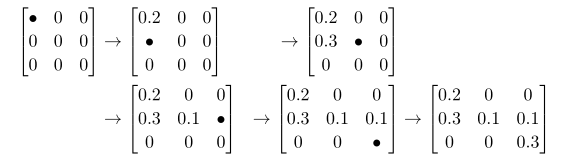
- 簡単なアルゴリズムとして,North-West Corner Ruleを提案
- 動作は図に示した式変形から分かる通り,$(1,1)$要素から決定していく
- memo: 式で$S_d$などが定義されていないが,もともと§2ではPermと書いていたものだと思われる
3.4の疑問な点
- NWルールを用いた結果構成される$P$がcoupling matrixであることは分かるが,これはvertexか?
- またProp3.4では外点であればサイクルを持たない,が言われているが,その逆を議論で使っているのではないか?(サイクルを持たないならば,外点)
次回
次回はGW前最後の回で,§3.5をやっていく